建模求解“隐形圆”中的单线段最值问题

广东省肇庆市广东肇庆中学(526040) 郑文龙

圆在初中数学中是一种十分重要的几何图形,也是中考题的重要载体.线段的最值问题也是初中几何的一个常见问题,但是只要动点的运动轨迹稍微复杂,特别是运动轨迹是一个“隐形圆”时,很多学生就找不到解题思路,无从下手.因此,本文结合2020年的广东中考数学考题,探究如何构造模型,求解“隐形圆”中的单线段最值问题.

1 中考试题呈现

例1(2020 广东中考卷)有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图1,∠ACB= 90°,点M、N分别在射线CA、CB上,MN长度始终保持不变,MN=4,E为MN的中点,点D到CA、CB的距离分别为4 和2.在此滑动过程中,猫与老鼠的距离DE的最小值为_____.

图1

解因为在RtΔMCN中,E为斜边MN的中点,所以CE== 2,如图2,以C为圆心,2 为半径作圆C,点E在圆C上,在ΔCED中,根据两点之间线段最短,得CE+ED≥CD,所以当C、E、D共线时,DE有最小值,因为CD=所以DE的最小值为

图2

2 构建模型

如图3,所求线段PA的两个端点分别是动点A和定点P,而动点A到另一定点O的距离为定值.根据圆的定义,点A在以O为圆心,AO为半径的圆上.从而把线段PA的最值转化成定点P到圆O的线段最值问题.

图3

当P、A、O共线时,PA有最值.

最小值PA′=OP −OA,最大值PA′′=OP+OA.

模型总结: 动点到另一定点的距离是定值,利用圆的定义,定圆心与半径,画圆形,得最值.

3 “隐形圆”的其它形式

3.1 直角定圆——以动点为顶点的角是直角

如图4,所求线段PA的两个端点分别是动点A和定点P,动点A是直角∠CAD的顶点.根据定理,90°圆周角所对的弦是直径,故点A在以CD为直径的圆O上.从而把线段PA的最值转化成定点P到圆O的线段最值问题.

图4

例2(2020 辽宁省初三零模)如图5,F为正方形ABCD的边CD上一动点,AB=2,连接BF,过A作AH⊥BF交BC于H,交BF于G,连接CG,CG为最小值为____.

解如图6,以AB的中点O为圆心,OA为半径直径画圆,因为∠AGB= 90°,所以点G在圆O上,当O、G、C共线时,CG有最小值,因为OC=所以CG最小值为√

模型总结: 动点是直角顶点,利用直角对直径,定圆心与半径,画圆形,得最值.

3.2 定角定圆——以动点为顶点的角是定角(非直角)

所求线段PA的两个端点分别是动点A和定点P,动点A为顶点的∠CAD是定角.如图7,当∠COD= 2∠CAD(∠CAD <90°),或 者 如 图8,当∠COD= 2(180°−∠CAD)(∠CAD >90°)时,∠CAD为圆周角,它所对的弦CD所对的∠COD为圆心角.点A在以O为圆心,OC为半径的圆上.从而把线段PA的最值转化成定点P到圆O的线段最值问题.

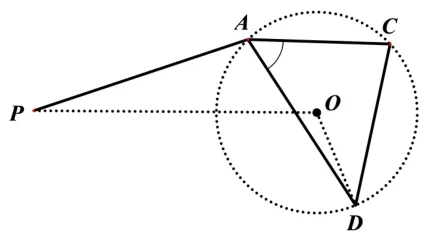
图7

图8

例3(2018 山东省中考模拟) 如图9,在RtΔABC中,∠ABC= 90°,∠ACB= 30°,BC=ΔADC与ΔABC关于AC对称,点E、F分别是边DC、BC上的任意一点,且DE=CF,BE、DF相交于点P,则CP的最小值为( )

图9

解如图10,连接BD,在RtΔABC中,∠ACB=30°,BC=所以∠BAC= 60°,AB= 2,AC= 4,因为ΔADC与ΔABC关于AC对称,所以∠BAD=120°,∠BCD= 60°,CB=CD,所以ΔCBD是等边三角形,所以BD=DC,因为DE=CF,∠EDB= ∠FCD=60°,所以ΔEDB∽= ΔFCD,所以∠EBD=∠FDC,因为∠FDC+∠BDF= 60°,所以∠EBD+∠BDF= 60°,所以∠BPD= 120°,所以点P在以A为圆心,AD为半径的圆上,当点A、P、C共线时,CP有最小值,所以CP的最小值为4−2=2,故选D.

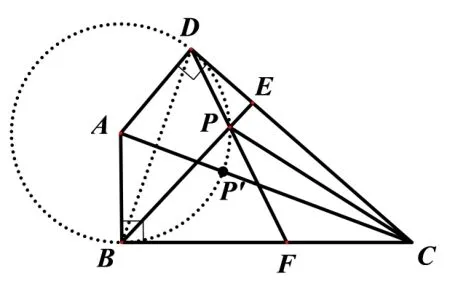
图10

模型总结: 动点是定角顶点,找它的对边,转化成圆心角,定圆心与半径,画圆形,得最值.

3.3 从动圆

如图11,所求线段PA的两个端点分别是动点A和定点P,另一个动点M在圆O上.点P、A、M共线,且PA与PM的比值为定值.此时,M是主动点,A是从动点.在PO上取点Q,使PQ:PO=PA:PM,由ΔPAQ∽ΔPMO,得到AQ是定值,故点A在以Q为圆心,QA为半径的圆上.从而把线段PA的最值转化成定点P到圆Q的线段最值问题.

图11

例4如图12,已知点A(3,0),C(0,−4),圆C的半径为2,点P为圆C上一动点,连接AP,若M为AP的中点,连接OM,则OM的最大值为_____.

图12

解如图13,取AC中点D,连接DM、CP,因为A(3,0),C(0,−4),在RtΔAOC中,AO= 3,OC= 4,AC=因为M为AP的中点,所以DM//CP,DM== 1,所以点M在以D圆心,1 为半径的圆上,当点O、D、M共线时,OM有最大值,所以OM的最大值是OD+DM=

模型总结: 主动点、从动点和定点共线,且主动点、从动点分别到定点的距离之比是定值,找主动点圆心与半径,通过缩放确定从动点的圆心与半径,画圆形,得最值.

3.4 旋转从动圆

如图14,所求线段PA的两个端点分别是动点A和定点P,另一个动点M在圆O上.其中∠ACM是定角,且AC与CM的比值为定值.此时,M是主动点,A是从动点.取点Q,使∠QCO= ∠ACM且QC:CO=AC:CM,由∠CAQ∽∠CMO,得到AQ是定值,得到点A在以Q为圆心,QA为半径的圆上.从而把线段PA的最值转化成定点P到圆O的线段最值问题.

图14

例5如图15,正方形ABCD中,AB=O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.求线段OF的最小值.

图15

解如图16,连接DO,作DM⊥DO且DM=DO,连 接MF,因 为DE⊥DF且DE=DF,所 以ΔDEO∽= ΔDFM,因为EO= 2,即E在以O为圆心,2为半径的圆上,所以MF=2,即F在以M为圆心,2 为半径的圆上,当点O、F、M共线时,OF有最小值,在RtΔDOC中,DO== 5,在等腰RtΔDOM中,MO=所以OF的最小值是

图16

模型总结: 主动点、从动点和定点连线形成定角,且主动点、从动点分别到定点的距离之比是定值,找主动点圆心与半径,通过旋转和缩放确定从动点的圆心与半径,画圆形,得最值.