不畏浮云遮望眼 终得云开见月明——对一道圆锥曲线联考题的探究拓展及教学思考

江苏省镇江市句容市江苏省句容高级中学(212400) 石秀成 汪勇建

圆锥曲线是高中数学解析几何单元的核心内容,也是高考数学必考的知识内容,且经常作为高考的压轴题出现,由此可见其本身的重要性和挑战性.圆锥曲线的挑战性一方面体现在其繁杂易错的运算量上,另一方面体现在联动表象下的定性关系,如定点定值等.因此对学生的数学运算、直观想象、逻辑推理等数学核心素养的要求较高.而圆锥曲线之间又有着许多共性和相似性,如果在解决问题的基础上进行抽丝剥茧,透过现象看本质,能够拓展出一般性的结论,将对问题的生成和理解有更深刻的认识,也是对数学核心素养的提升.本文笔者通过一道圆锥曲线联考题来进行探究和拓展,引导学生把握命题规律、看清试题本质,以期为数学的教学和学习提供一些思考.

1 试题呈现

(2020年镇江大市联考第22 题) 在平面直角坐标系xOy中,有三条曲线:= 1(0< m <4),=1(n>0),3○y2=2px(p>0).

请从中选择合适的一条作为曲线C,使得曲线C满足:点F(1,0)为曲线C的焦点,直线y=x −1 被曲线C截得的弦长为8.

(1)请求出曲线C的方程;

(2)设A,B为曲线C上两个异于原点的不同动点,且OA与OB的斜率之和为1,过点F作直线AB的垂线,垂足为H,问是否存在定点M,使得线段MH的长度为定值?若存在,请求出点M的坐标和线段MH的长度;若不存在,请说明理由.

2 试题解答

解: 选择曲线3○y2=2px(p>0).

(1) 点F(1,0) 为曲线C的焦点,所以= 1,解得p= 2,即y2= 4x.设直线y=x −1 与曲线C交于P(x1,y1),Q(x2,y2)两点,联立y=x −1 与y2=4x消元得x2−6x+1=0,显然Δ>0,由韦达定理得x1+x2=6.因为直线y=x −1 过焦点F,故弦长PQ=x1+x2+p=8,满足条件,所以曲线C的方程为y2=4x.

(2)由题意可知,显然直线AB的斜率存在且不为零,直线AB不过原点,设直线AB的方程为x=ty+b(b ̸=0),与抛物线y2=4x联立得y2−4ty−4b=0,Δ′=16(t2+b)>0,设由韦达定理得y3+y4= 4t,y3y4=−4b.因为OA与OB的斜率之和为1,所以kOA+kOB== 1,解得b=−4t,故x=t(y −4),直线AB过定点T(0,4).过点F作直线AB的垂线,垂足为H,则H在以FT为直径的圆上,故当点M为圆心,即线段FT的中点时,有线段MH的长度为定值,此时点M的坐标为线段

评析: 本题是一道开放性题型,开放性题型是新高考模式下的新题型,但这方面的资源稀缺,课堂训练较少,因此开放性题型目前是学生的短板.本题对学生来说有两个难点:首先是曲线的选择上,并不是三个曲线都符合题意,需要借助已有的知识和结论排除不符合条件的选项; 其次是在第(2)问的问法上,会让学生如丈二和尚摸不着头脑,难以弄清切入点,要设什么以及求什么,这就需要高屋建瓴,透过表征看本质,其本质就是直线过定点问题.虽然本题的运算量并不大,但侧重考察了抽丝剥茧、层层深入的分析能力,更重点突出了数学运算、逻辑推理等数学核心素养的考查.本题考法新颖,内涵丰富,是一道值得研究的好题.

3 探究拓展

《普通高中数学课程标准》指出:“教学应基于学生已有的基础知识,从具体实例出发,展现数学知识的发生、发展过程,使学生能够从中发现问题、提出问题,经历数学的发现和创造过程,了解知识的来龙去脉.”数学家波利亚也曾说:“解题就像采蘑菇,当你发现一个蘑菇时,它的周围周围可能有一个蘑菇圈.”

本题中的第(2)问本质上说明了这样一个事实: 过抛物线的顶点O作两条直线,分别与抛物线交于A、B两点,若OA与OB的斜率之和为非零定值,则直线AB过定点.于是我们不禁有如下思考:

(1)过抛物线上任意一点作斜率之和为非零定值的两条直线,且与抛物线分别另交于A、B两点,则直线AB是否也过定点?

(2)过抛物线上任意一点作斜率之积为非零定值的两条直线,且与抛物线分别另交于A、B两点,则直线AB是否也过定点?

(3)在椭圆和双曲线中是否也有类似的结果?

带着上面的疑惑,笔者进行了深入的探究与思考,得到了如下的拓展结论.

结论1: 若P(x0,y0) 是抛物线C:y2= 2px(p >0)上任一点,过P作两条斜率之和为定值c(c ̸= 0) 的直线分别与抛物线C交于A、B两点,则直线AB恒过定点

证明: 显然直线AB的斜率不为零,故设直线AB的方程为x=ty+b,与抛物线C的方程y2= 2px联立消元得y2−2pty −2pb= 0,Δ = 4p2t2+8pb >0.设A(x1,y1),B(x2,y2),由韦达定理得:

因为PA与PB的斜率之和为常数c,所以有kP A+kP B==c,因为P、A、B都满足抛物线C的方程y2=2px,所以

带入(*) 式得=c,化简得b= (y0−,代入直线AB方程x=ty+b可得x= (y+y0−故直线AB恒过定点

结论2: 若P(x0,y0) 是抛物线C:y2= 2px(p >0)上任一点,过P作两条斜率之积为定值c(c ̸= 0) 的直线分别与抛物线C交于A、B两点,则直线AB恒过定点

证明: 显然直线AB的斜率不为零,故设直线AB的方程为x=ty+b,与抛物线C的方程y2= 2px联立消元得y2−2pty −2pb= 0,Δ = 4p2t2+8pb >0.设A(x1,y1),B(x2,y2),由韦达定理得:

因为PA与PB的斜率之积为常数c,所以有kP A ·=c,因为P、A、B都满足抛物线C的方程y2=2px,所以

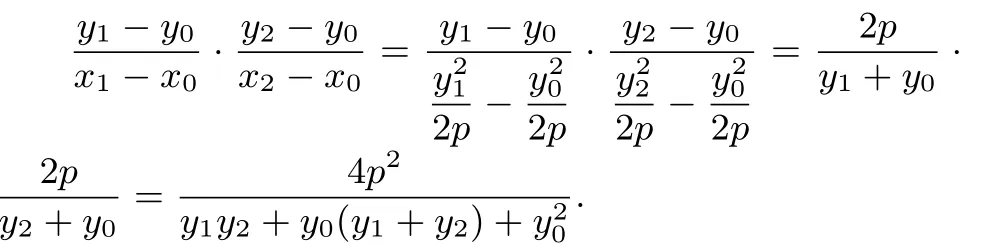
带入(*) 式得=c,化简得b=y0t+ (x0−),代入直线AB方程x=ty+b可得x= (y+y0−故直线AB恒过定点

结论3:若P(x0,y0)是椭圆=1(a>b>0)上任一点,点A、B是C上两点.

(1) 若kP A+kP B=λ(λ ̸= 0),则直线AB恒过定点

(2) 若kP A ·kP B=λ(λ ̸=则直线AB恒过定点

结论4: 若P(x0,y0)是双曲线C:= 1(a,b >0)上任一点,点A、B是C上两点.

(1)若kP A+kP B=λ(λ ̸= 0),则则直线AB恒过定点

(2)若kP A·kP B=λ(λ ̸=−),则直线AB恒过定点

青岛总督府邸旧址室内地毯铺装方式是直接将地毯铺设在地板之上，利用地毯自身与地面摩擦力吸附在其上.主要铺设在需要静音的房间，如书房、卧室、会客室等.从仅存的历史照片可以识别出德租时期大接待室中使用浅色花环图案的编织地毯；儿童游戏室则铺设浅色背衬深色蔓叶纹样的地毯.遗憾的是地毯使用寿命较短，目前尚未发现德租时期遗留的原物遗存.

结论3、4 的证明与结论1、2 相仿,此处便不一一赘述.

4 源远流长

本题第(2)问给同学们遮上了一层面纱,唯有揭开面纱,方见其本来面目,其本质上就是是直线AB过定点T,H在以FT为直径的圆上运动,所以存在圆心M,使得MH的长度恒为以FT为直径的圆的半径,也就是直线过定点问题可谓是解析几何中的经典问题,在高考中也是可见一斑,比如下面高考真题.

(2020年山东高考第22 题) 已知椭圆C:1(a>b>0)的离心率为且过点A(2,1).

(1)求C的方程;

(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明: 存在定点Q,使得|DQ|为定值.

上述高考题的第(2)问本质是结论3 中的特例,限于篇幅,不再给出两题的解答过程,通过对比,不难发现本题的第(2)问更像是两道高考题的一个综合改编,由此可见题目之间的内在联系,源远流长.“问渠哪得清如许,为有源头活水来”,这也提醒我们的学生在平时的做题过程中,要多思多想多联系,去追寻问题的根源,才能有活水涌来滋润我们的思维,焕发出智慧的生机.在解题的过程中,还要注意层层深入、抽丝剥茧,透过现象看清问题的本质,发现问题的共性,要学会对同宗同源的问题进行延续发掘,总结这一类问题的一般方法和结论,从而达到“会当凌绝顶,一览众山小”的眼界.

5 教学思考

课本是最重要的教学资源,课本中的例题、习题都是经过长时间打磨的,也是经历了时间检验的,其丰富的内涵和典型的代表性以及广泛的推广性是高考命题的源泉,高考题中有不少题与课本中的例题习题有着千丝万缕的联系,有的是课本改编,有的甚至就是课本原题.因此我们要重视课本教材,而不只是停留在口头上,“用教材教,而不是教教材”,有些老师上课就是读教材,课后习题也没有挖掘拓展,这是十分不可取的,我们要通过课本的例题和习题的示范作用,让学生能对一般问题驾轻就熟,系统掌握课本知识体系和内在联系,形成良好的认知结构.

(2)加强动手操作,算无遗策

数学是研究数量关系和空间形式的学科,运算在数学教学中几乎无处不在,章建跃先生说:“数学学习的基本任务是学会运算和推理”,良好的运算能力是解题的保障,教师在教学过程中应该加强和巩固学生的运算能力.圆锥曲线对学生来说之所以是一座难以逾越的大山,其中一个原因就是其繁杂庞大的计算量让学生望而却步,学生在做圆锥曲线的题目时经常算不下去望题兴叹,或者一步算错步步算错,甚至有学生就干脆放弃了,由此可见运算的重要性.学生运算能力的低下,也与教师的重视程度不够有关,教师在课堂教学中,应该多给学生一点运算的时间和空间,同时也应该指导学生优化计算,让学生养成准确、合理、迅速、简洁的运算素养.

(3)提升核心素养,强“研”欢笑

核心素养是育人价值的集中体现,数学教学应该以发展学生的数学核心素养为导向,创设合适的情境,启发学生思考与钻研,进而把握数学问题的本质.在圆锥曲线教学中,不能强硬的灌输给学生“按步走”的解题套路,要教给学生读懂题目、把握本质的能力,以本题为例,命题专家通过对问题的包装和打扮,将定点定值的常规题型打造成了压轴题,学生如能去其表象,挖其本质,定能快速上手,解决问题.在圆锥曲线的教学中,教师可以选择一个典型试题,引导学生层层深入钻研进去,再抽丝剥茧探索出来,发现题目背后的奥秘和本质,总结出自己的理解和体会,真正做到触类旁通、举一反三,最终达成提升数学学科素养,拥抱数学学习的目的.