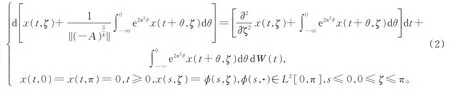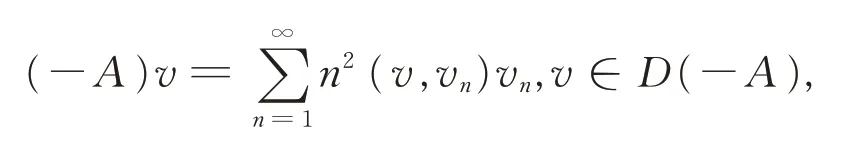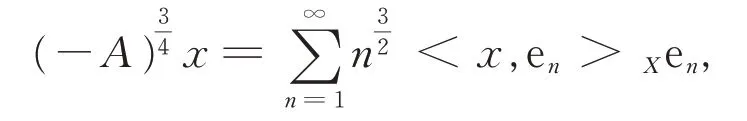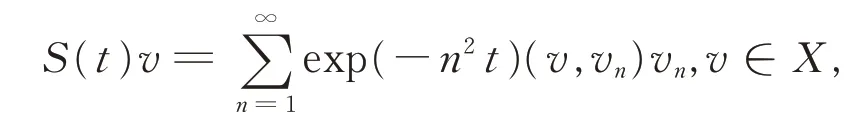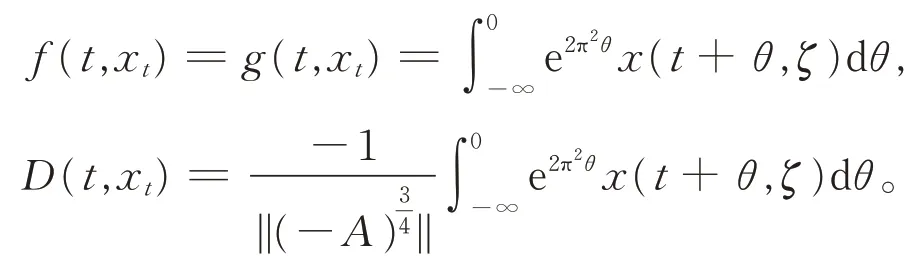Hilbert空间上无穷时滞中立型随机偏泛函微分方程适度解的存在唯一性
2021-10-13余国胜
余国胜
(江汉大学人工智能学院,湖北武汉 430056)
0 引言
长期以来,众多学者研究了有限时滞中立型随机偏泛函微分方程适度解。文献[1]给出了Hilbert空间随机泛函微分方程适度解的存在唯一性和渐近行为。文献[2]讨论了Hilbert空间上半线性中立型随机微分方程适度解的存在唯一性。文献[3]考虑了中立型随机偏泛函微分方程适度解的指数稳定性。文献[4]探讨了脉冲中立型随机偏泛函微分方程适度解的均方指数稳定性。文献[5]研究了有限时滞中立型随机偏微分方程适度解的指数稳定性。
有限时滞在上述结果的推导中起到十分重要的作用。近年来无穷时滞系统越来越受到人们的关注。文献[6]考虑了相空间为BC((-∞,0];Rn)无穷时滞随机泛函微分方程解的存在唯一性。文献[7]推广了文献[6]的结果。文献[8]讨论了一类无穷时滞随机泛函微分方程的鲁棒性。文献[9]探究了非线性无穷时滞中立型随机泛函微分方程的一般衰减稳定的鲁棒性。文献[10]考虑了无穷时滞中立型随机泛函微分方程的LaSalle型定理。由于伊藤公式不适用于适度解,加上中立项和无穷时滞的存在,这无疑给相关研究带来了难度。本文在已有文献的研究基础上,拟讨论Hilbert空间上无穷时滞中立型随机偏泛函微分方程适度解的存在唯一性。
1 预备知识
(Ω,ℑ,{ℑt}t≥0,P)是完备的概率空间。{ℑt}t≥0满足通常条件,即它是递增右连续且I0含所有的P零测集。H,K是两个实可分的Hilbert空间,<∙>H,<∙>K表示内积,|∙|H,|∙|K相应地表示向量范数。W(t)是定义在完备概率空间(Ω,ℑ,P)上取值于可分Hilbert空间K的Wiener过程,其增量协方算子为Q。{ℑt}t≥0是由{W(s),0≤s≤t}生成的ℑ代数,于是W(t)是关于{ℑt}t≥0的一个鞅。令βn(t)(n=1,2,…)是(Ω,ℑ,{ℑt}t≥0,P)上相互独立的一列一维实值标准Wiener过程,则≥0,其中vn≥0(n=1,2,…),{en}(n=1,2,…)是K中完备 标准正交基。Q是正定的自伴迹类算子,即Qen=vnen,其中<∞,则K值随机过程W(t)称为QWiener过程。
定义1[11]令σ∈L02,定义
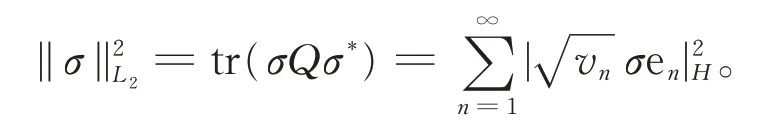
假设S(t)是无穷小生成元为A的一致有界解析半群。令0<α≤1,则可定义分数幂算子(-A)α,它是定义域为D((-A)α)的闭线性算子,具体详见文献[12]。对于给定的r>0,相空间Cr定义为
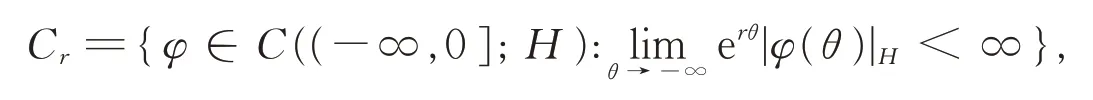
其 中,C((-∞,0];H)是 从(-∞,0]到H的连续函数全体。Cr是具有范数||φ||r=的Banach空间,L2(Cr)记为ℑ,可测Cr值随机过程且有<∞,具体详见文献[13]。
我们考虑如下无穷时滞中立型随机偏泛函微分方程系统为
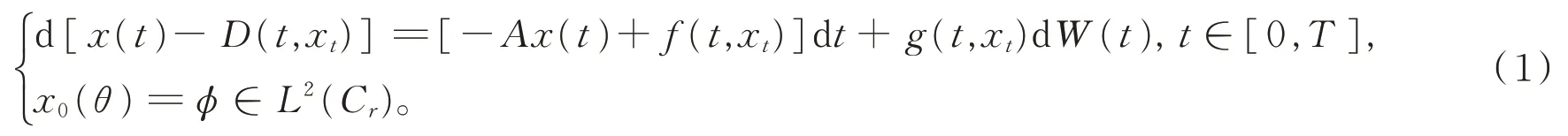
映 射(-A)αD:[0,∞)×L2(Cr)→H,f:[0,∞)×L2(Cr)→H,g:[0,∞)×L2(Cr)→(K,H)是3个可测映射。
定义2如果过程x(t)满足以下条件,则称x(t)为系统(1)的一个适度解。
1)x(t,ω)是一个从[0,T]×Ω到H的可测函数,且x(t)是ℑt适应的;
3)过程x(t)满足如下方程
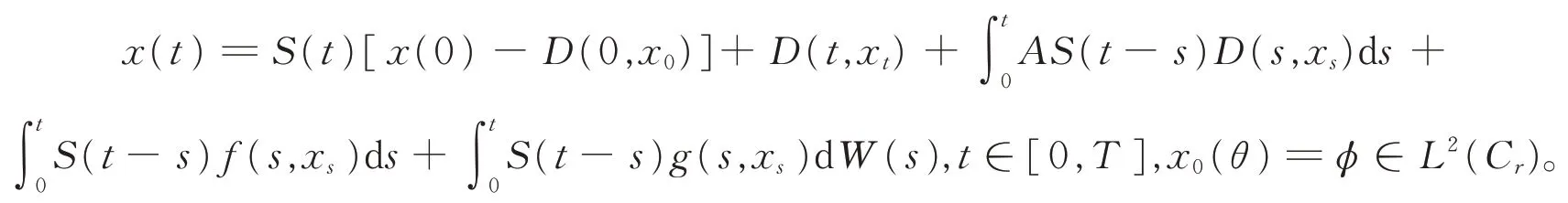
引理1[12]令-A是解析半群S(t)的无穷小生成元,如果0∈ρ(-A),则有
1)存在常数M≥1和γ>0使得
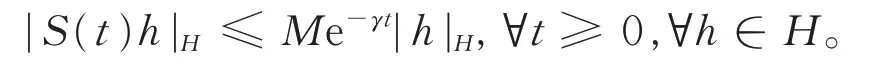
2)对于0<α1<,存在常数≥1,使得分数幂算子满足
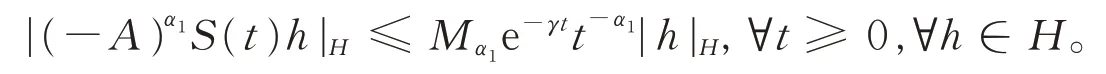
3)当0<α≤1,h∈D((-A)α),存在常数Nα≥1,使得
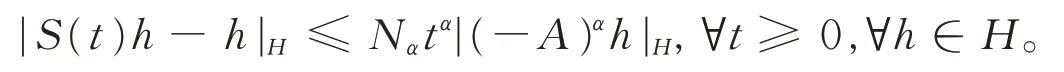
对于系统(1),有如下假设:
A1)0∈ρ(-A)。
A2)对任意的φ,ψ∈Cr和0≤t≤T,存在两个正常数L1,L2使得
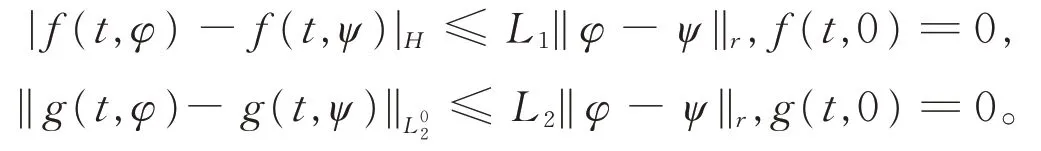
A3)存在0<α≤1,D(t,∙)∈D((-A)α),则有
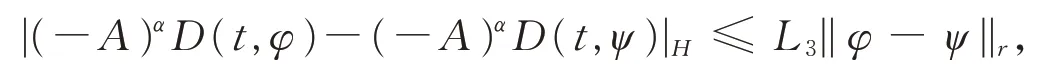
其中,L3>0,且。
2 主要结果
取T>0,DT是属于C((-∞,T],L2(Ω,Cr))的所有连续过程z全体,且||z||DT<∞,这里

在DT上引进下列映射:
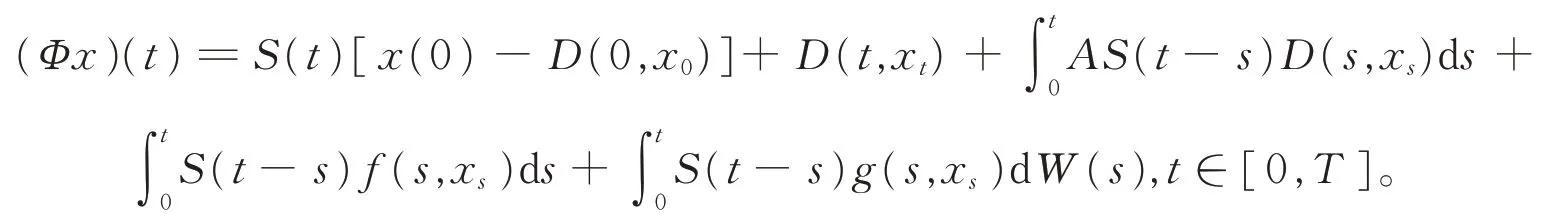
引理2对于∀x∈DT,在L2意义下(Φx)(t)在区间[0,T]上是连续的。
证明令0 由引理1有 由Burkholder-Davis-Gundy不等式可以得到 注意到x∈DT,当t2→t1时,I1,I2,…,I8均趋向于0,引理2得证。 引理3算子映射Φ和DT定义如上,则Φ(DT)⊂DT。 证明令x∈DT,有 故有||Φx||DT<∞。 定理1假设A1),A2)和A3)成立,则系统(1)在[0,T]上存在唯一的适度解。 证明令x,y∈DT,有 注意到||(-A)-α||L3<,可取充分小的T1>0,得到一个正实数B(T1)∈(0,1),使得 由Banach不动点定理,系统(1)在(-∞,T1]上存在唯一的适度解。反复操作,便可以将其扩充到在(-∞,T]上,定理得证。 例1考虑无穷时滞中立型随机偏泛函微分方程系统为 其中,W(t)是定义在完备概率空间(Ω,ℑ,P)上的Wiener过程。 令X=L2[0,π],Y=R。定义A:X→X,-A=,其定义域为D(-A)={v∈X:v,是绝对连续,∈X,v(0)=v(π)=0},则 其中,vn(ζ)=sinnζ(n=1,2,…)是-A的特征向量组成的正交基。 A是X上解析半群S(t)的无穷小生成元,其中 且||S(t)||≤exp(-π2t),t≥0,因此它是一个压缩半群。 相应地 取r=π2,L1=L2=L3=,则有 (责任编辑:胡燕梅)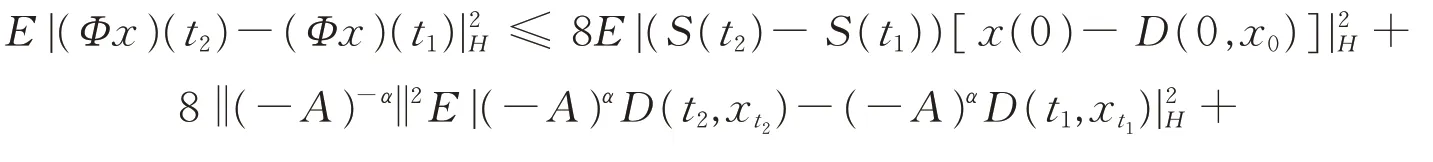
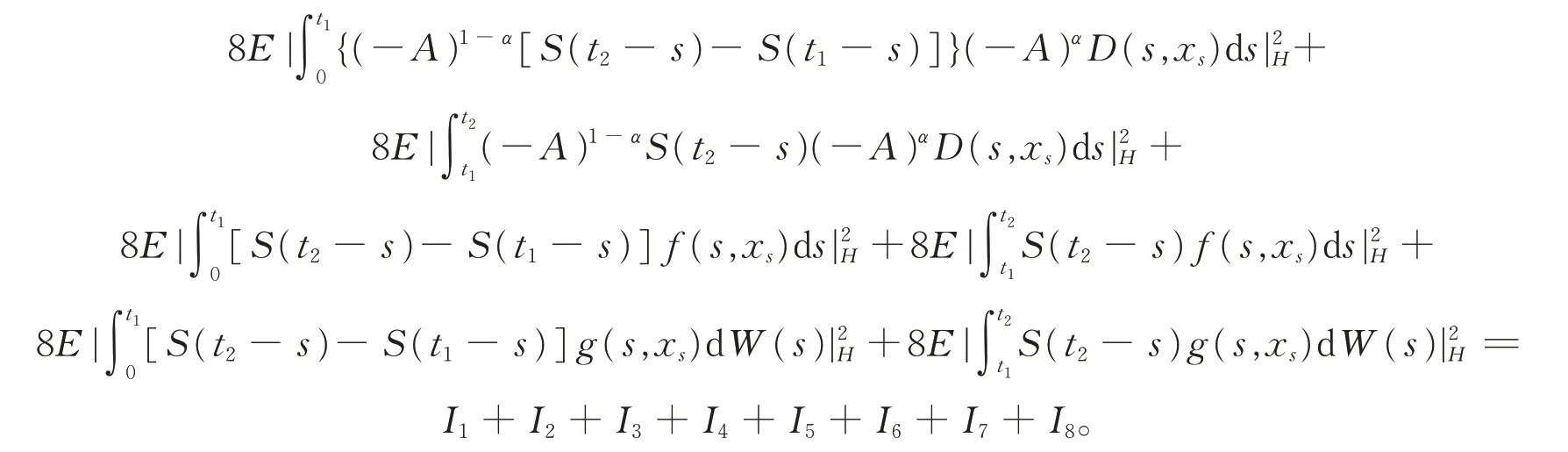
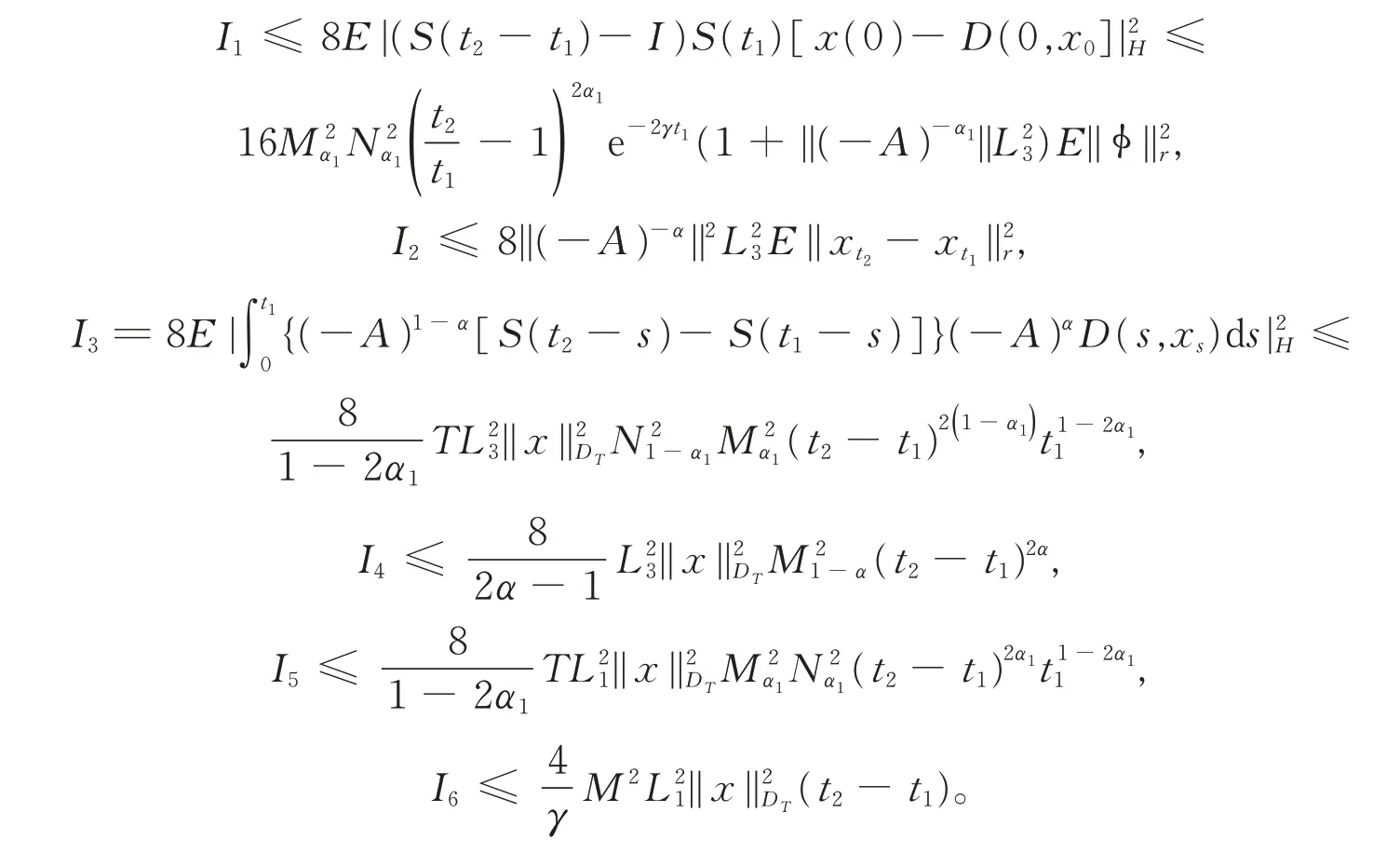
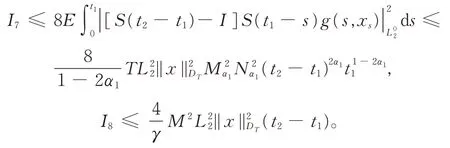
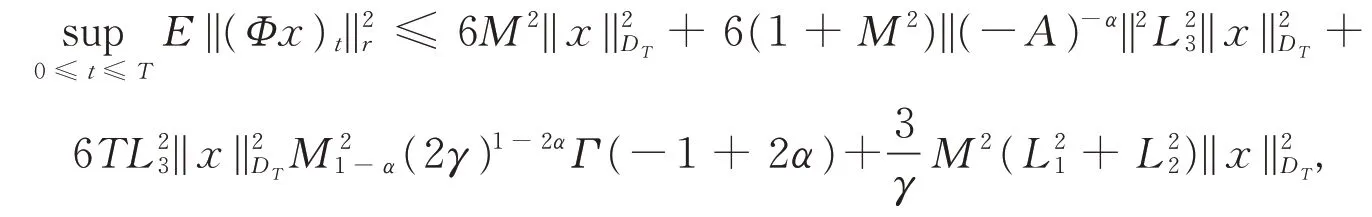
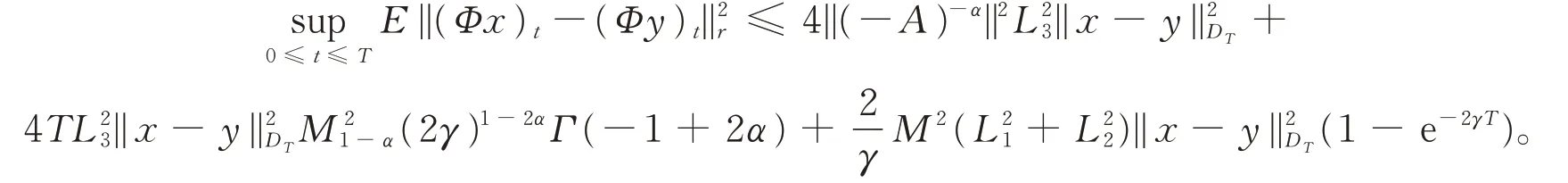
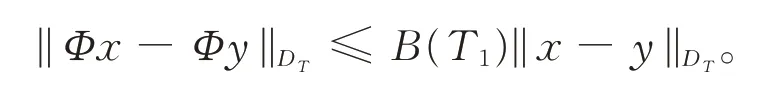
3 实例