基于FDS的CI柜体随机振动加速试验方法

秦伟，王鹏，刘悦，唐梓迪

（株洲中车时代电气股份有限公司，湖南 株洲 412001）

铁路是我国重要的基础设施之一，是运输行业中的支柱。随着铁路高速化和重载化发展进程的加快，对车载设备的安全性及可靠性提出了更高的要求。振动环境作为影响设备可靠性的关键因素，一般认为，在运输或服役过程中，设备所处的随机振动环境为平稳高斯分布，但实际中，设备所承受的加速度振动载荷也会表现出明显的超高斯分布[1]。振动载荷的超高斯分布特性会加速结构的疲劳损坏，对产品的影响不可忽视。研究表明[2]，在功率谱密度及RMS值相同的情况下，相比于高斯随机振动的来说，超高斯随机振动产生的疲劳损伤要大得多。现在铁路车辆设备在出厂前的振动冲击环境模拟主要是采用高斯随机振动方法进行的，导致很多在实验室通过国标规定的随机振动试验的产品，在实际使用过程中又出现较多的失效。为提高机车车辆设备的可靠性，在实验室内开展模拟符合现场振动条件的随机振动就显得极为重要。

高速动车牵引变流器是列车的核心部件，其可靠性决定了列车能否正常运行。笔者从随机振动试验方法的角度出发，研究了一种以疲劳损伤为纵坐标的响应谱，即疲劳损伤谱[3]，分别给出了在时域和频域中计算FDS的方法。然后基于FDS的等效疲劳损伤原则，对牵引变流器柜体进行随机振动试验加速方法的研究。

1 疲劳损伤谱及其获取方法

疲劳损伤谱是激励信号本身的一种特性，类似于冲击响应频谱（SRS）[4]。区别在于，SRS是寻找每个单自由度系统下的峰值响应，而疲劳损伤谱是激励信号在得出不同固有频率下的响应后，采用疲劳线性累积理论，并结合S-N曲线计算每个频率对应的损伤值。因为它考虑了频率的影响，与伪损伤值相比，能更准确地反应载荷信号对实际结构的破坏能力。获取疲劳损伤谱主要有基于频域和时域两种途径。

1.1 频域计算方法

如果实测加速度信号平稳，且其概率密度服从高斯分布，则可根据加速度功率谱密度计算疲劳损伤谱。假设在每个共振峰的半功率带宽上（rn2Bfξ= ），加速度功率谱PSD必须近似一致性，且系统阻尼满足ξ≤0.1。设p(S)是应力峰值处的概率密度函数，T是在该应力环境作用下的总时间，可得损伤求解公式为：

此外，在这种假设下，无论加速度激励信号的概率密度函数是否服从高斯分布，系统的响应都将近似为高斯分布，并且应力响应峰值的概率密度将近似服从瑞利分布[5]。应力峰值的瑞利分布函数见式（2）。

式中：S为应力峰值；σs为应力时间历程的均方根值。

通过式(2)中给出的峰值概率密度函数求解式(1)，可推导出的疲劳损伤为：

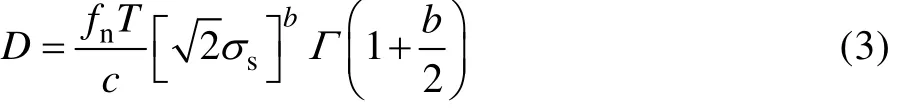
式中：Γ( )定义为的Gamma 函数。

速度与应力呈现出比例关系[6-7]，可进一步将式(3)写为：

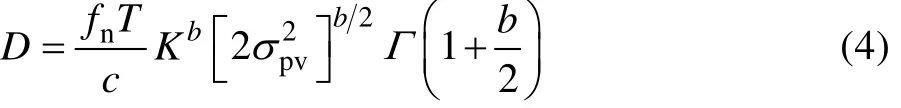
式中：K为比例常数；σpv为速度时间历程的均方根值RMS；c、b为疲劳曲线的参数，即公式N=c*S-b中的参数。

通过加速度功率谱密度Ga(fn)，求得σpv为：

式中：Q为品质因子。

将速度时间历程的均方根值σpv代入式(4)中，得出在频域下由加速度功率谱密度计算疲劳损伤的最终表达式为：

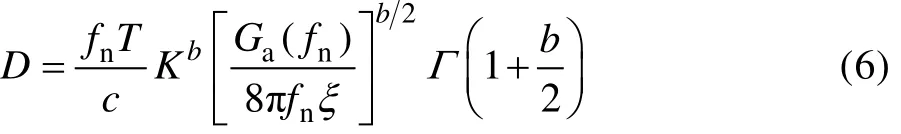
通过式(6)计算不同频率点的损伤值。

1.2 时域计算方法

对于非平稳或非高斯振动，可基于时域的方法获取疲劳损伤谱。经实测获取振动环境的加速度时间历程，并采用多项式最小二乘法对其进行去趋势处理。由于速度与应力呈现出比例关系，因此将处理后的加速度激励信号依次经过多个单自由度系统，获得不同频率下的速度响应信号。对于求解单自由度系统响应，采用Smallwood[8]提出的改进递归数字滤波法，其中加速度激励信号与速度响应信号之间的传递函数为：

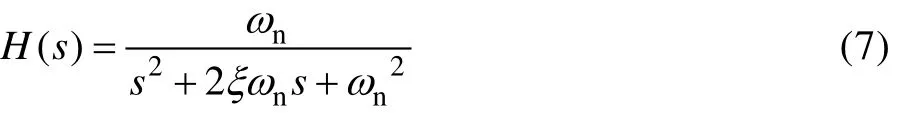
式中：ξ为阻尼比；ωn为固有圆频率，且ωn=2πfn，fn为系统固有频率。

将式(7)进行Z变换得:

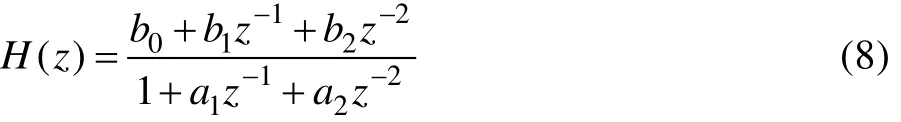
其中：

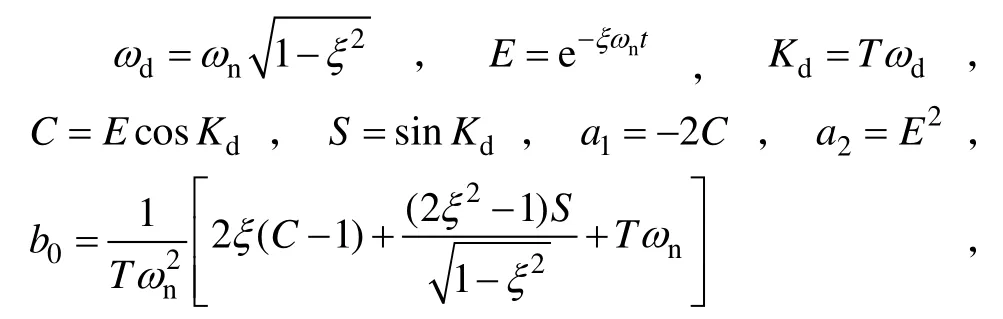
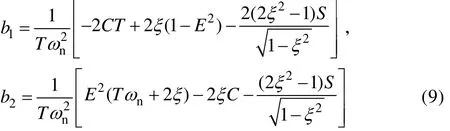
式中：T为信号采样间隔。

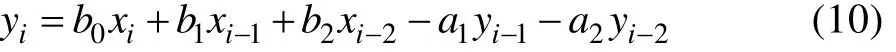
求解单自由度系统响应，获取不同频率下的速度响应信号后，对每个响应信号进行雨流计数获得循环谱，并结合S-N曲线及疲劳线性累积理论，计算每个频率下的累积损伤：

式中：Si为应力幅值；ni为对应应力幅值Si的循环次数；Ni为在应力幅值Si的作用下导致失效的循环次数；c为比例常数；b为材料的疲劳指数。

速度大致与应力成比例关系，常数为K。则推导出损伤计算公式为：

式中：ivP为速度幅值；ni为所对应速度幅值ivP的循环次数。

通过式(12)计算不同频率下的损伤，并绘制出损伤与频率的关系曲线，进而得出疲劳损伤谱。

2 疲劳损伤谱算法准确性验证

频域方法相对于时域方法而言，避免了对响应信号进行雨流计数处理，计算量缩减显著。频域方法要求加速度激励信号平稳，且其概率密度需服从高斯分布，因此在计算疲劳损伤谱时，该方法具有一定的局限性。在时域方法下，无需考虑振动类型，可针对任意加速度时域信号进行疲劳损伤谱计算。鉴于此，笔者采取一段平稳的高斯随机振动信号，分别基于频域方法和时域方法计算疲劳损伤谱，来验证两者产生的FDS曲线是否具有一致性。选取GB/T 21563—2018[9]中1类A级车体安装的PSD频谱，作为振动台加速度激励，在此过程中，通过加速度传感器测得控制系统所输出的时域激励信号。标准中指定的PSD量级（垂向）见表1。

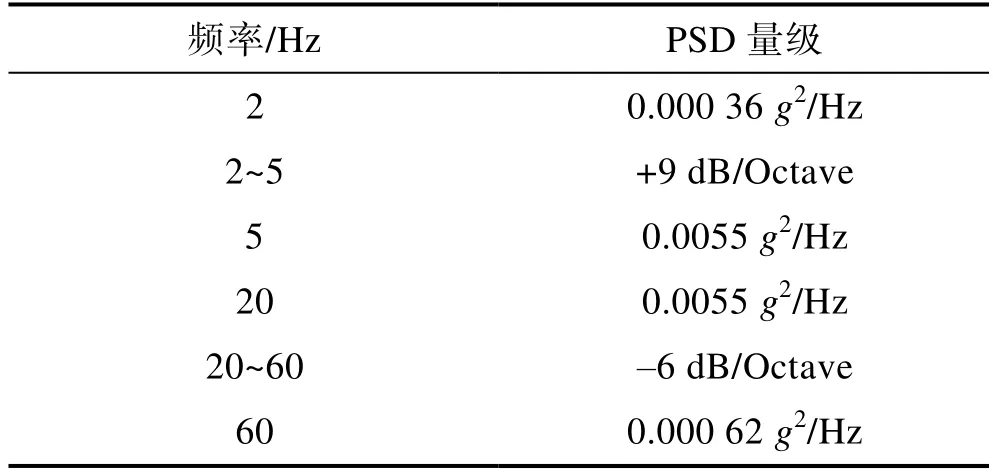
表1 PSD量级（垂向） Tab.1 The PSD magnitude (vertical)

截取一段时长为20 s的平稳加速度信号，其加速度功率谱密度（垂向）如图1所示。实线代表通过实际测量激振信号计算得出的PSD，频率间隔为0.2 Hz；虚线为标准中给定的PSD。对比发现，两者的PSD量级吻合，因此在基于频域方法计算FDS时，采用经实测加速度信号计算得出的PSD，从而在一定程度上减小了由于实际采集过程中所产生的误差，使得频域FDS和时域FDS对比结果更加精确。

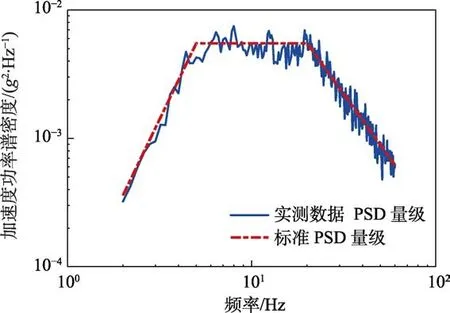
图1 加速度功率谱密度曲线 Fig.1 Acceleration power spectral density curve

在疲劳损伤谱计算过程中，基于频域方法和时域方法，两者所涉及到的参数基本一致，即阻尼比ξ、系统刚度K、材料疲劳曲线的参数c和b值。阻尼比ξ和b值将影响疲劳损伤谱曲线的形状，设定时必须格外慎重，应尽量符合实际情况。c和K的改变只会导致疲劳损伤谱曲线沿y轴缩小或者放大，曲线形状并不会变化。通常情况下，并不考虑某个激励信号的疲劳损伤谱绝对数值，而是将不同信号的疲劳损伤谱进行对比。对于多个载荷信号，只要采用相同的c和K值，它们的疲劳损伤谱的比例关系就保持不变。因此将K和c的取值都设定为1，以简化计算。该小节的目的是验证频域和时域算法所获取的疲劳损伤谱是否具有一致性，而未涉及到具体的产品及其材料参数，因此在计算中设定Q值为10，b值为8，并以1/12倍频程选取频率点。时域方法下获取FDS的算法如图2所示。

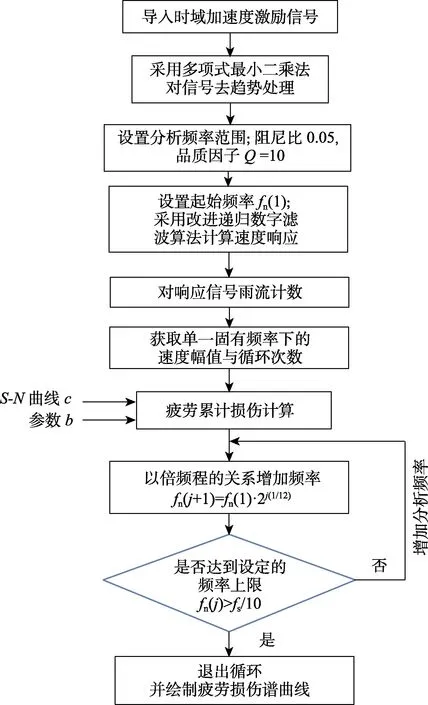
图2 时域获取FDS的算法 Fig.2 Algorithm for obtaining FDS in time domain

对比图3中的FDS曲线，针对平稳的高斯振动信号，采用时域算法和频域算法计算的疲劳损伤谱是一致的，以此验证了疲劳损伤谱算法的准确性。

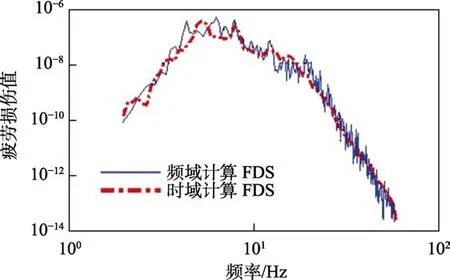
图3 疲劳损伤谱对比 Fig.3 Comparison of fatigue damage spectrum

3 CI柜体随机振动加速试验

3.1 实测振动信号时域计算FDS

对于牵引变流器柜体所处的实际振动环境，笔者将采集的平稳超高斯数据（垂向加速度采集数据，峭度值k=5），截取一段时间为t=30 s的加速度信号，如图4所示。时域计算FDS，将K和c的取值设定为1，采用典型金属材料的疲劳曲线参数b=4，依据试验被测的阻尼特性，选定阻尼比值为0.025。

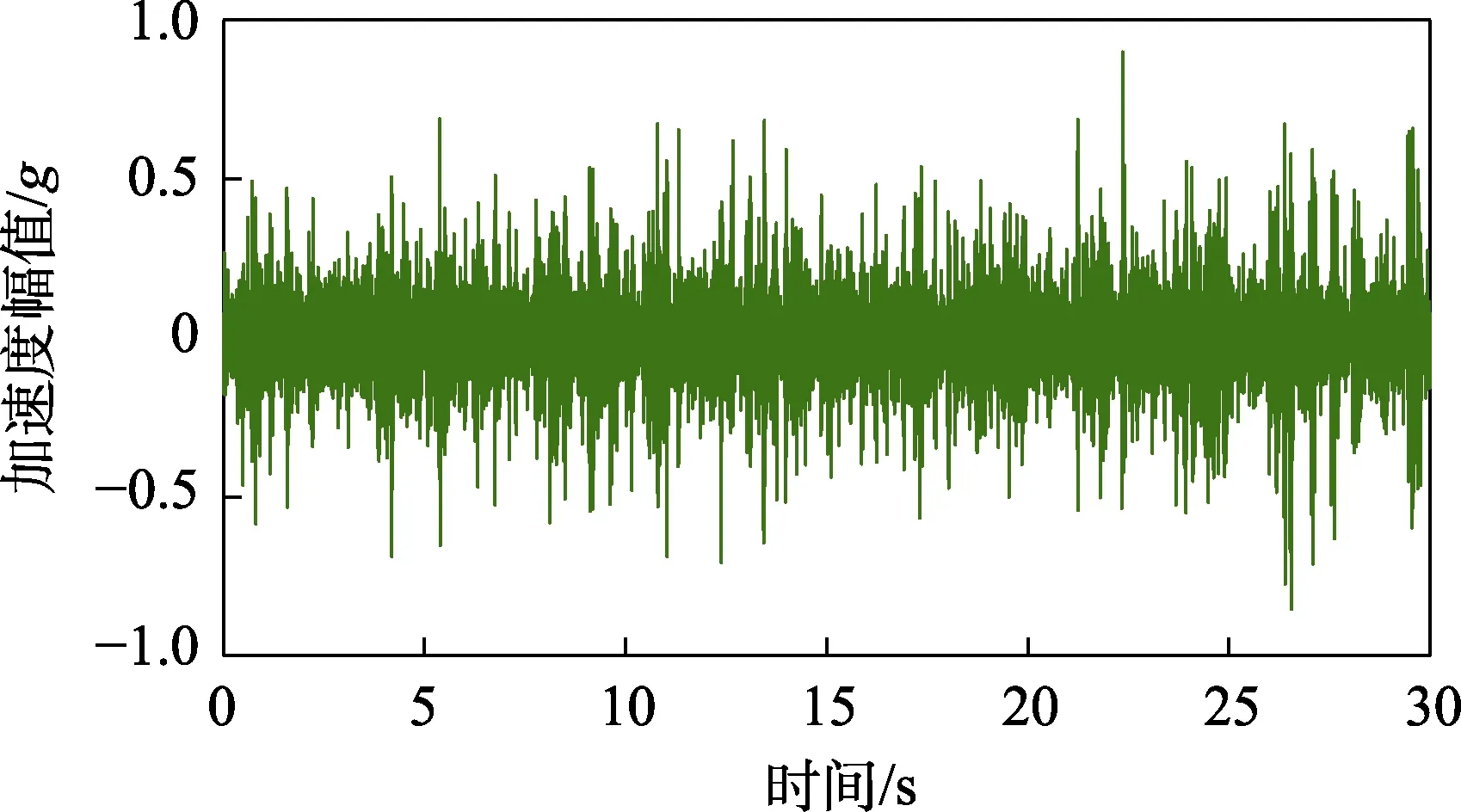
图4 实测加速度激励信号（垂向） Fig.4 Measured acceleration excitation signal (vertical)

GB/T 21563—2018中要求试验产品的运行寿命需达到25%的正常寿命（正常寿命按25 a，每年工作300 d，每天工作10 h计算），即总时间T=18 750 h。经时域方法计算t=30 s的疲劳损伤谱Dt，从而通过总时间T估算出累积损伤DT[10]。FDS曲线如图5所示。

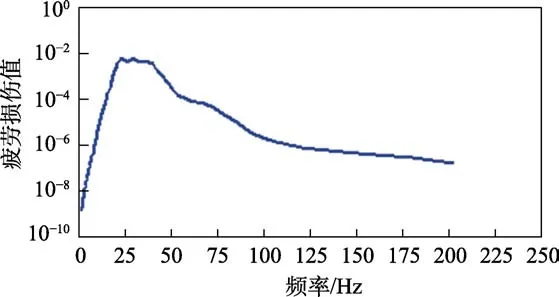
图5 载荷信号的FDS曲线 Fig.5 FDS curve of load signal

3.2 试验过程

对于不同频率点fn处的疲劳损伤值，可通过式(14)得出与原始加速度激励信号具有相同损伤当量的平稳高斯振动的加速度功率谱。式(14)由逆求式(6)所得：

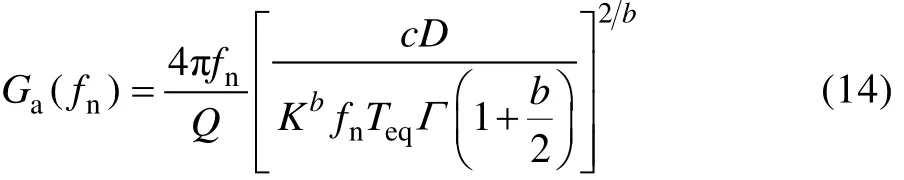
式中：Teq为设置的试验时间。

设置试验时间为Teq=18 000 s，计算求得振动台试验PSD，如图6所示。为了避免过度加速，必须对加速后的试验PSD谱进行检验，即将振动台试验PSD谱通过式(15)进行最大响应加速度谱（ERS）[10]计算。极限响应谱表示持续时间为T的随机振动作用在一系列单自由度系统所得到的最大响应相对固有频率的包络。在试验中，为避免样品出现不符合实际的过载现象，要求计算的ERS值不应超过冲击响应谱对应最大值的1.5倍[11]。如图7所示，ERS曲线未超出SRS曲线，说明试验加速合理，加速的试验PSD谱可应用到振动台试验中。

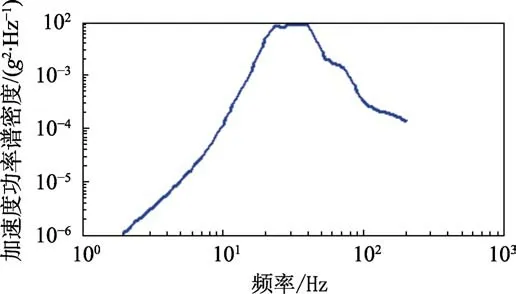
图6 振动台试验PSD Fig.6 PSD for shaking table test

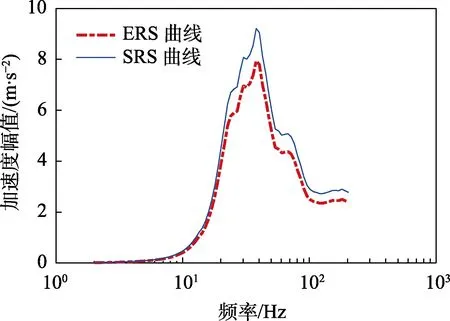
图7 ERS与SRS曲线对比 Fig.7 Comparison of ERS and SRS curves

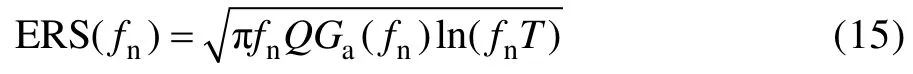
式中：Ga(fn)表示频率为fn的加速度PSD量级；T为PSD的持续时间。

对控制器输入振动台试验PSD量级，按照加速试验时间对牵引变流器柜体进行随机振动试验，检测整个柜体的耐久性能。牵引变流器随机振动试验安装状态如图8所示。

图8 变流器垂向安装状态 Fig.8 Vertical installation status of converter

与传统的牵引变流器模拟长寿命试验相比，虽然试验时间一致，但该振动台试验的PSD量级是依据损伤等效原则，经实测超高斯信号的FDS计算得出的，因此更加真实地模拟了产品的随机振动环境。对柜体垂向加载，试验结果显示，在该方向的随机振动下，未出现任何疲劳失效，并采用同样的方法验证了在其他方向上也未出现故障，则认定该试验样品耐久性能良好。该试验方法可操作性强，并且对于其他产品的随机振动试验具有一定的借鉴指导意义。

4 结语

通过时域方法计算超高斯加速度信号的疲劳损伤谱，并采用等效疲劳损伤原则，将获取的FDS曲线，转换为具有同等损伤当量的平稳高斯振动的PSD谱。将该PSD谱进行ERS计算，与时域加速度信号的冲击响应谱作比较，以此避免了过度加速。利用转换的PSD谱对牵引变流器柜体进行了随机振动加速试验，与传统的振动试验相比，该方法保证了与原始超高斯信号相同的损伤当量，更加真实地模拟了CI柜体的振动环境。同时，该方法为其他产品的随机振动试验研究提供了一定的技术支持。