PCA和SDG融合的天然气脱水装置故障诊断

2021-10-13熊伟马豪张波龙俨丽尹爱军

装备环境工程 2021年9期

熊伟，马豪，张波，龙俨丽，尹爱军

（1.中国石油西南油气田分公司重庆气矿，重庆 400021；2.重庆大学机械工程学院，重庆 400044）

天然气脱水装置作为一种化工流程生产系统，具有反应机理复杂、工艺流程连续，较强的非线性、时变性及耦合性等特点，并且生产过程中数据处理量大、复杂性强，部分关键指标难以实现在线监测，因此对其进行故障诊断存在着较大的难度。目前常用的诊断方法在实际应用中难以取得令人满意的效果[1]，而一旦出现的故障未被及时发现和处理，又容易造成较大的经济损失，故其生产过程中的安全性极为突出[2]。随着大数据技术的产生和发展，将大数据中的相关方法应用到流程工业的诊断领域体现出广阔的应用前景。

主成分分析法（PCA）和符号有向图法（SDG）在故障诊断领域均有大量的应用。主成分分析法作为一种多变量统计方法[3-4]，无需对过程建立严格的物理模型，且通用性较强。如李荣雨提出了一种滑动窗口PCA的故障隔离算法[5]。杨洁针对注塑成形工艺，提出了一种基于PCA的过程监测方法[6]。SDG模型是一种基于知识的图模型，通过定性的因果关系，反映各监测变量之间的相互影响，有利于解释故障的传播模式和精确定位故障源，因而在化工行业中应用广泛[7-8]。王峰、高金吉等[9]就提出了基于层次分析法的SDG-HAZOP方法，并用于对硝基苯初馏塔装置的HAZOP分析。美国以Venkatasubramanian教授为首的研究团队，对SDG方法作出改进，并在工业应用方面取得了重大进展[10]。文中将两种方法结合起来，先用PCA法对天然气脱水装置进行过程监控，得到各参数变量的残差贡献图，再根据建立的SDG模型及相应的推理规则，对该贡献图作出解释，从而诊断出脱水系统故障的根源，达到了定性方法与定量信息结合的良好效果[11]。

1 基于PCA的异常检测

当脱水装置处于稳定运行的工况时，通过采集的各监测变量历史数据建立的主元模型，可以很好地解释当前各变量实测值之间的相关关系，其中SPE和T2统计量分别用于衡量主元模型的有效程度和系统过程的可控水平，故此时两者均能维持在一个平稳波动的状态。当脱水装置出现故障而偏离正常运行时，各监测变量之间的相关性也会随之遭到破坏[12-13]，并造成T2和SPE统计量的异常增大，因此可以求出在线监测数据的T2和SPE统计量，并与正常运行下的控制限进行比较，从而判断当前阶段脱水系统是否出现故障。

假设对脱水装置的m个监测参数共进行了n次独立重复观测，其结果为X′n×m。对其进行标准化处理后，可求出协方差矩阵cov(X)。对该矩阵进行特征分解后，得到各特征值及其特征向量。对特征值从大到小排序，并采用信息贡献率累计法确定主元个数。一般设置主元所包含的信息累计贡献率为85%。

则T2统计量为：

式中：t为主元向量；S为前k个特征值构成的对角矩阵。T2统计量的分布近似地服从F分布[14]，取显著性水平为90%，从而确定脱水装置正常运行下的T2控制限。

SPE统计量为：

式中：x为标准化后的m维实时监测数据向量；P为前k阶特征向量构成的负载矩阵。通常正常工况下的脱水过程数据服从正态分布，故SPE统计量近似服从卡方分布[15]。取置信度为95%，从而确定脱水装置正常运行下的SPE控制限。

残差贡献率反映出故障时刻各监测变量对该故障产生的贡献度大小，其中第j个变量在第i时刻对SPE统计值的贡献率为：

式中：Xij为变量实测值；为变量在主元子空间的重构值。

2 基于SDG的脱水装置故障诊断模型

2.1 SDG及其故障推理规则

符号有向图（SDG）是一种用定性图形[16]反映系统过程及设备的方法，具有简单直观，易于解释的特点，同时还能挖掘故障在流程系统内部的传递过程[17]。就脱水装置而言，图中的节点既可以用来表示天然气脱水工艺流程中的某一具体参数（如闪蒸罐液位、重沸器温度控制阀开度、吸收塔差压等），还可用来表示脱水系统中的某一故障事件（如三甘醇循环管路堵塞，精馏柱盘管穿孔等）。其中参数类节点的正负号表示该监测参数的值是否偏高或偏低，连接箭头表示系统各参数之间的影响关系，通常用实线（虚线）箭头表示故障事件与变量或变量之间为正向（负向）激励作用。对于给定的SDG模型，所有节点在相同时刻状态观测值的集合称为一个瞬时样本，在SDG中进行搜索可以得到该样本已经发生偏离的节点及支路传播路径[18]。这种方向一致且已经产生影响的若干支路形成的通路称为相容通路，相容通路即为故障信息传播的路径[19]。

SDG模型应用于故障诊断中的推理方式主要为反向推理[20]。在瞬时样本已知的情况下，由下游报警节点出发推理上层节点的可能状态，并与实际监测到的节点状态相比较。若吻合，则说明该条路径可能正确，以此类推搜索出系统中所有可能的相容通路。但这种方式在应用过程中容易出现故障源的多异性结果，导致诊断分辨率低[21]。因此当得到的相容通路不止一条时，需从中判断哪条通路能最大限度解释现存的异常参数，并将其对应的故障源作为诊断结果，具体流程如图1所示。

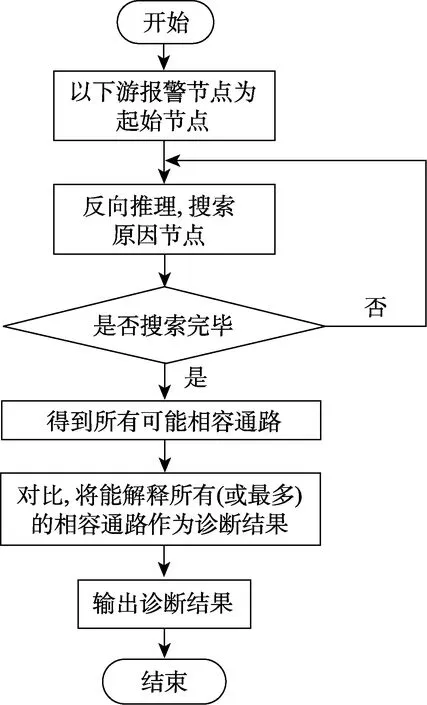
图1 SDG模型故障推理机制 Fig.1 Failure reasoning mechanism of SDG model

2.2 脱水装置SDG模型

由于脱水装置具有监测参数众多、形式复杂、化简推导困难等特点，采用数学方程来建立SDG模型的方法并不可行，故此处采用流程图和经验知识相结合的建模方法。其具体步骤为：1）根据脱水工艺流程（见图2）将整个装置分解为若干较为简单的设备级单元，确定每个设备可能的失效形式作为故障节点；2）对每个故障节点进行故障树分析，找出其对应的异常参数及相关关系；3）建立各个设备单元的局部SDG模型；4）将各局部SDG模型在公共节点处合并，形成脱水装置整体的SDG模型；5）模型的化简与完善。

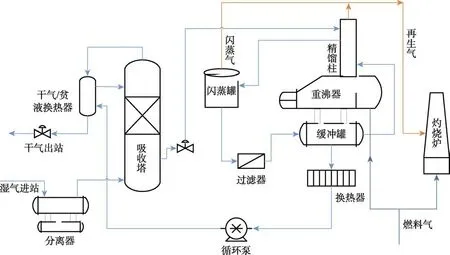
图2 脱水装置工艺流程 Fig.2 Process flow of dehydration device

针对脱水装置及其典型故障建立的SDG模型如图3所示。根据脱水工艺过程，当精馏柱盘管出现穿孔类故障时，热量的对外散失首先会导致精馏柱顶部温度及精馏性能的下降，使得三甘醇重沸腾再生的效果变差，造成三甘醇贫液浓度达不到要求，而贫液浓度的降低最终会造成干气露点偏高。与此同时，精馏柱顶部三甘醇富液的漏失会导致进入闪蒸罐的三甘醇明显减少，表现为闪蒸罐液位控制阀的开度和闪蒸罐液位均低于正常值。依照类似的分析，便能得到脱水装置的整体SDG模型。

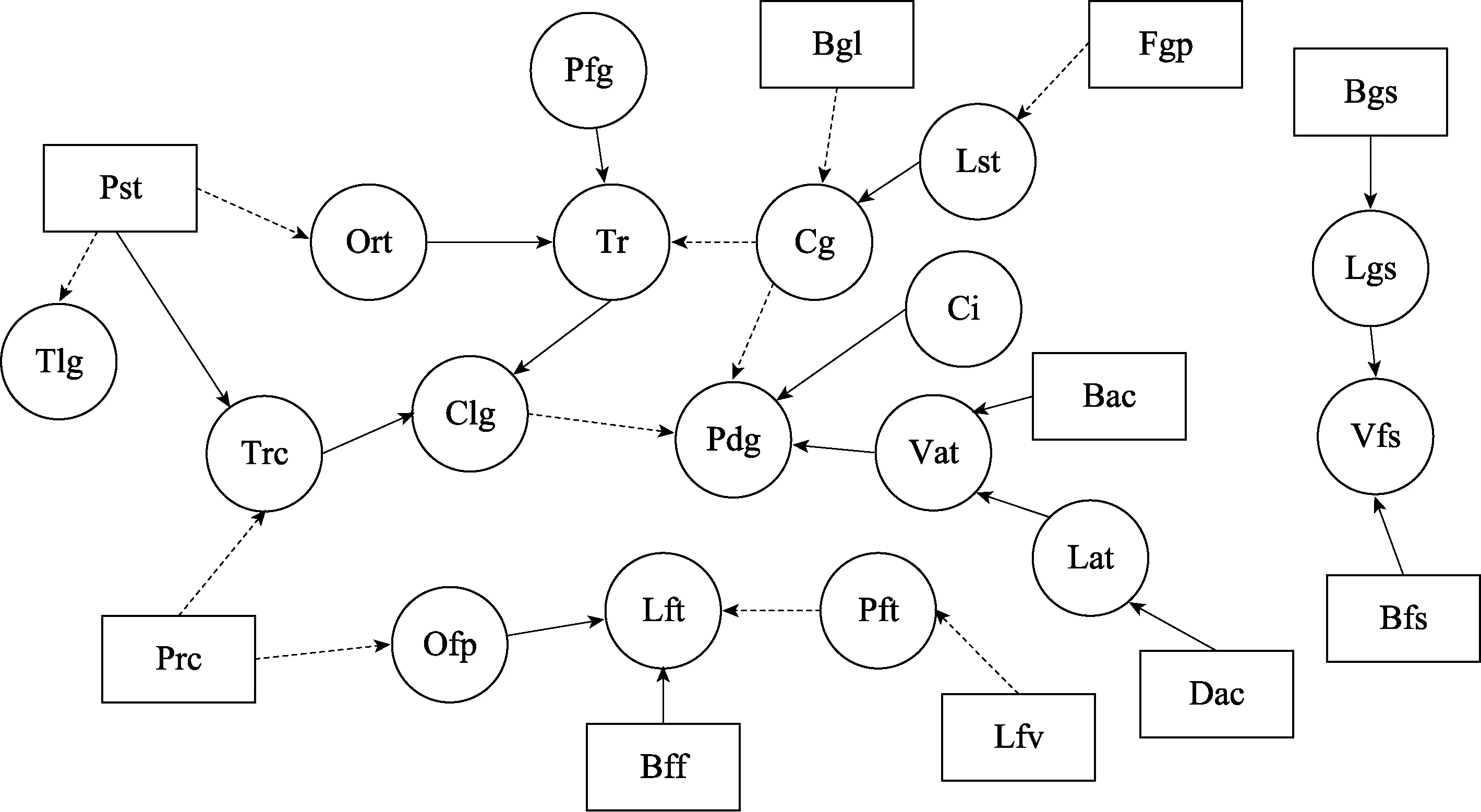
图3 脱水装置SDG模型 Fig.3 SDG model of dehydration device

该SDG模型能够准确反映脱水装置中各变量之间的因果关系，各参数节点和故障节点的符号含义见表1、表2。

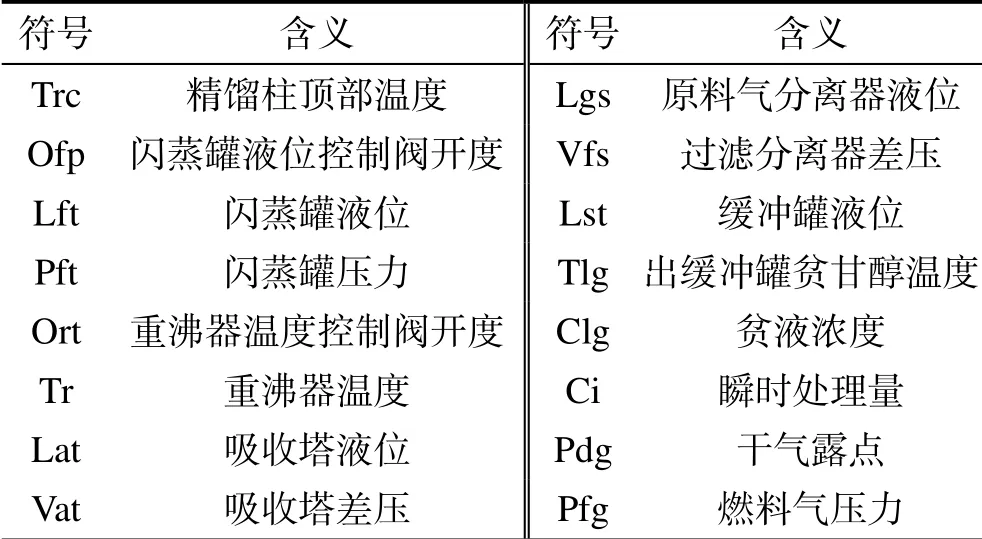
表1 SDG模型中各参数节点的符号含义 Tab.1 The meanings of each parameter node in SDG model

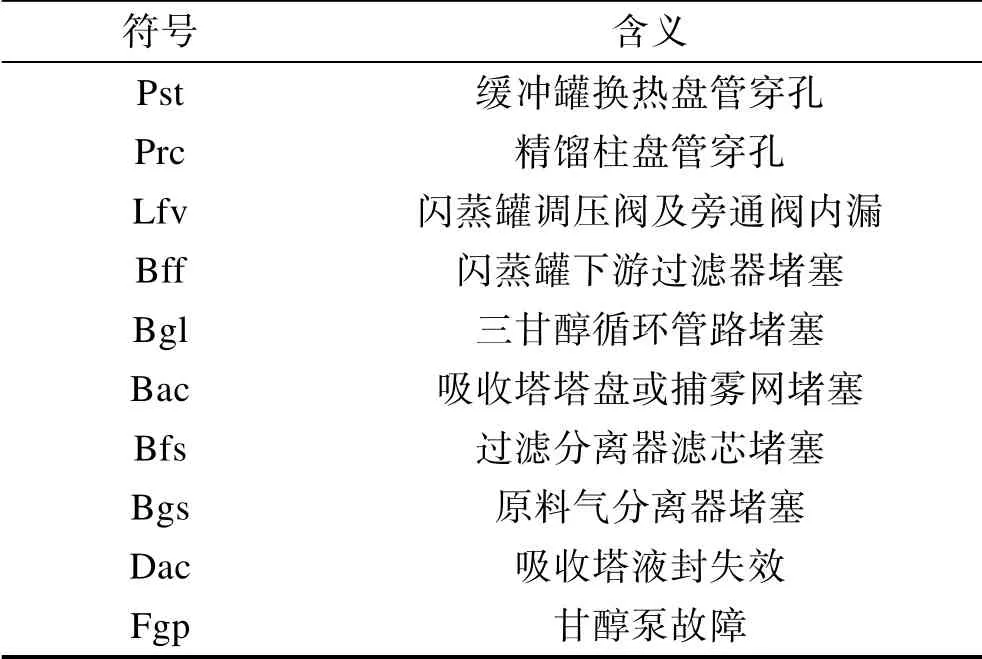
表2 SDG模型中各故障节点的符号含义 Tab.2 The meanings of each fault node in SDG model

2.3 PCA-SDG脱水装置故障诊断流程

基于PCA-SDG的脱水装置故障诊断具体实施步骤如下：

1）采集脱水装置正常运行时的过程数据X′n×m，对其进行标准化处理及主成分分解后，得到主成分模型。

2）计算出脱水系统正常运行下T2和SPE统计值的控制限。

3）导入在线监测到的过程数据，并根据已建好的主元模型，计算T2和SPE统计量。

4）若T2和SPE统计量的值均超出控制限，则表明系统运行出现异常。

5）求出各变量对超限SPE统计量的贡献率，得到异常变量及其符号，从而实现对脱水装置异常参数的识别。

6）根据SDG模型及其推理规则，搜索确认造成这些异常参数的设备故障源。

3 应用案例

3.1 现场设备介绍

中石油重庆气矿七桥中心站扩建100万脱水装置如图4所示。该装置由天然气脱水系统和三甘醇再生系统组成，主要包含吸收塔、重沸器、精馏柱、闪蒸罐及缓冲罐等设备。共有监测参数33个，见表3。

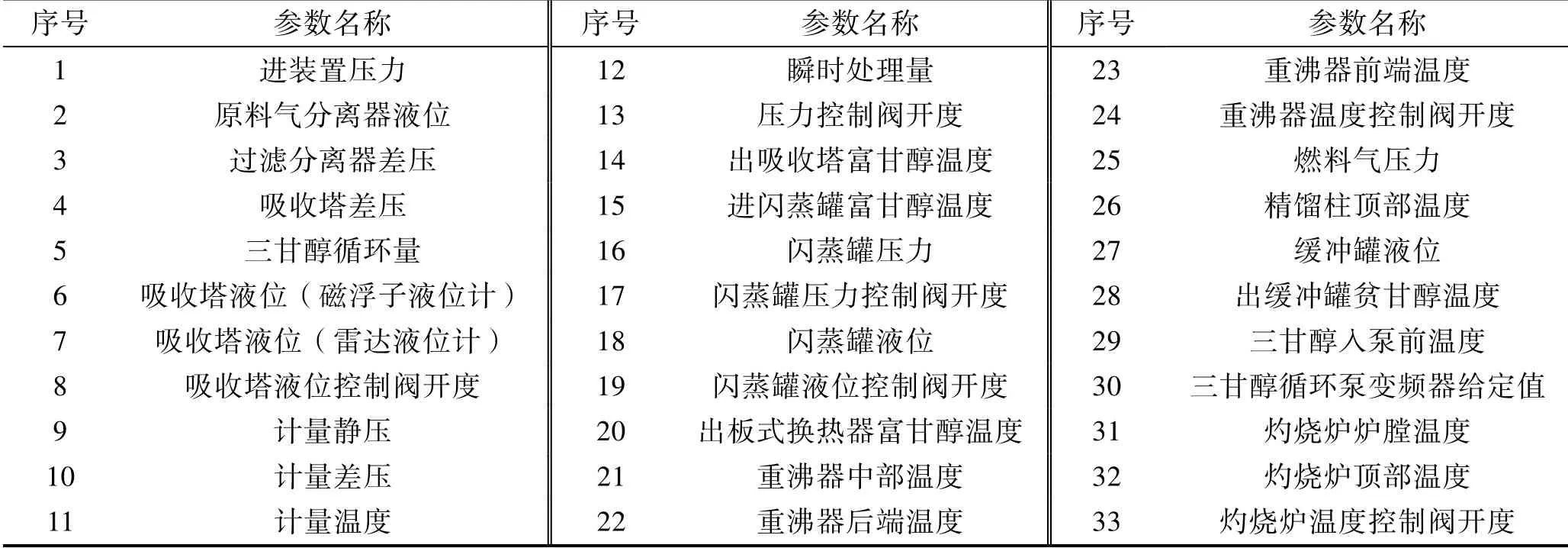
表3 脱水装置监测参数及代号 Tab.3 Monitoring parameters and codes of dehydration device

图4 脱水装置现场 Fig.4 Site map of dehydration device

3.2 案例分析

七桥中心站脱水装置各监测参数的采样间隔为5 s，根据SDG模型，从中选取19个监测参数进行诊断。将11月5日上午8—9时的实测数据作为正常工况下的原始数据矩阵用于建立主元模型，对其经过标准化处理后，求出协方差矩阵Σ，进一步对矩阵Σ进行特征分解，便能得到包含原始数据85%以上信息的各个特征值，以及由特征向量构成的负载矩阵。此处按照信息贡献率累积法确定的特征值数为7，故原始数据在主元空间经降维变换后的主元个数为7。紧接着将采集到的包含某故障记录在内的30 min数据（共360个采样点）引入主元模型，得到降维处理后各个主元的变化曲线，如图5所示。

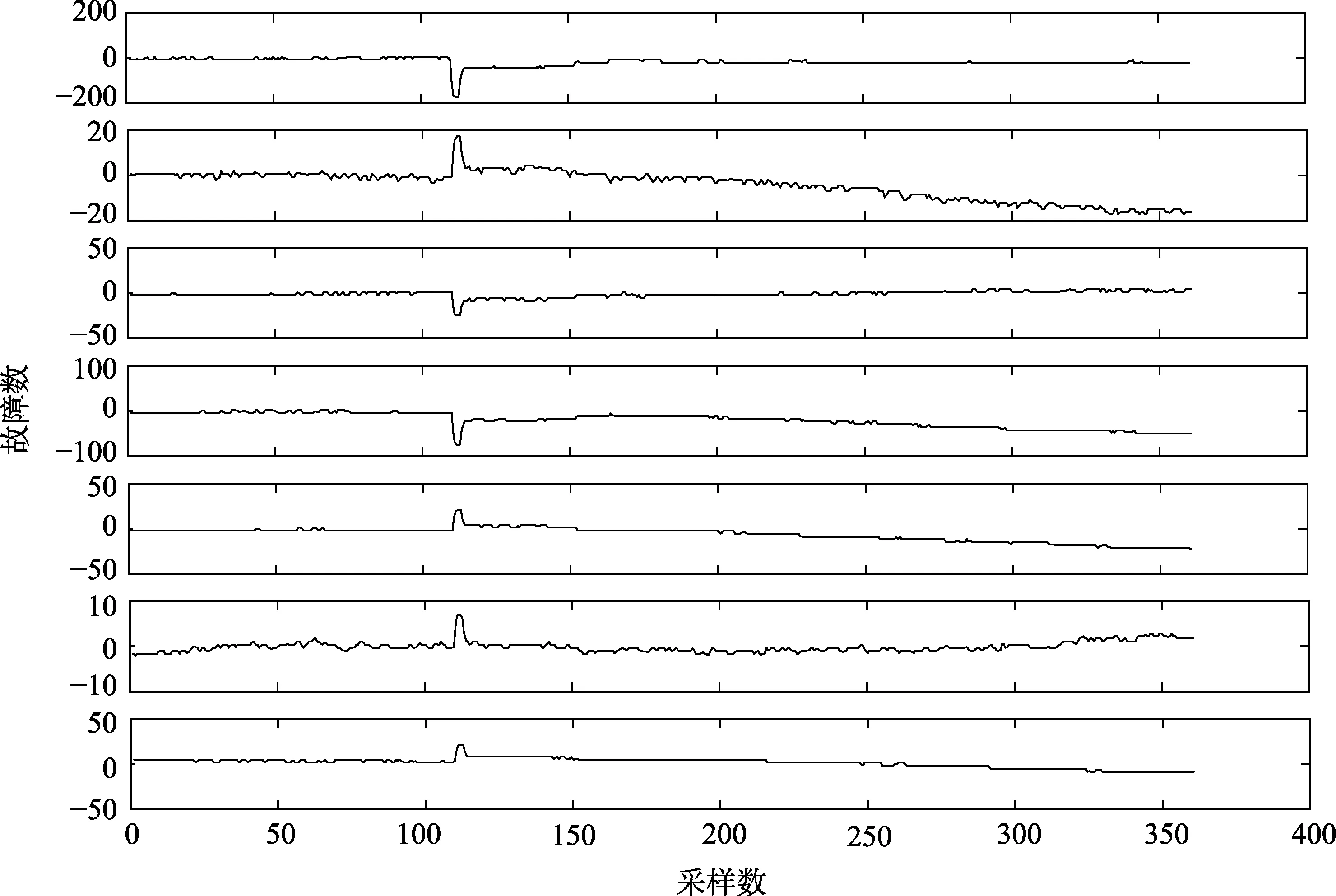
图5 故障数据的主元曲线 Fig.5 Principal component curves of fault data

由主元分量的数据还难以识别故障对应的具体异常参数，故需要借助于统计量的构造予以准确识别。结合式（1）、（2）算出每一采样时刻T2和SPE统计量的值，假设正常运行时的T2统计量服从F分布，并取显著性水平为90%，SPE统计量近似服从卡方分布，并取置信度为95%，可求出脱水装置T2和SPE统计量阈值分别为141和20。最终得到故障时段内T2统计量和SPE统计量的变化曲线分别如图6、7所示。

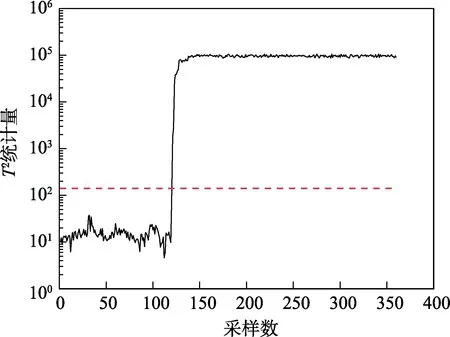
图6 故障数据的T2统计量 Fig.6 T2 statistics graph of fault data

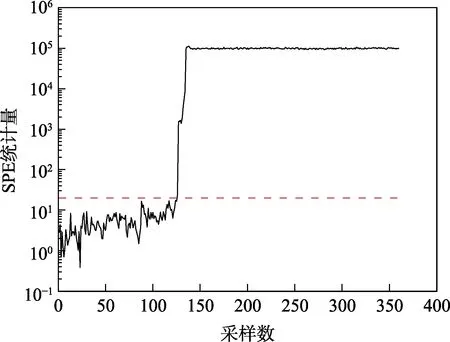
图7 故障数据的SPE统计量 Fig.7 SPE statistics graph of fault data

可以看出，在第125个采样点附近，两条曲线均出现阶跃式上升，并随后一直保持在高于控制限的范围。根据PCA过程监控规则，即可判定系统在该采样点处发生了故障。需要注意的是，即使处在正常运行，也可能出现个别采样点的统计量超出控制限的状况，但在作出判断时不应考虑此类离群点的影响，否则容易造成虚警。由式（3）求取对应采样时刻各个变量的残差贡献度（如图8所示），并通过设定阈值范围确定异常参数。其中，上限阈值选取范围为，下限阈值选取范围为，其中m为参数个数，Qα为SPE统计量的控制限[22]，此处设定上下限阈值分别为和：

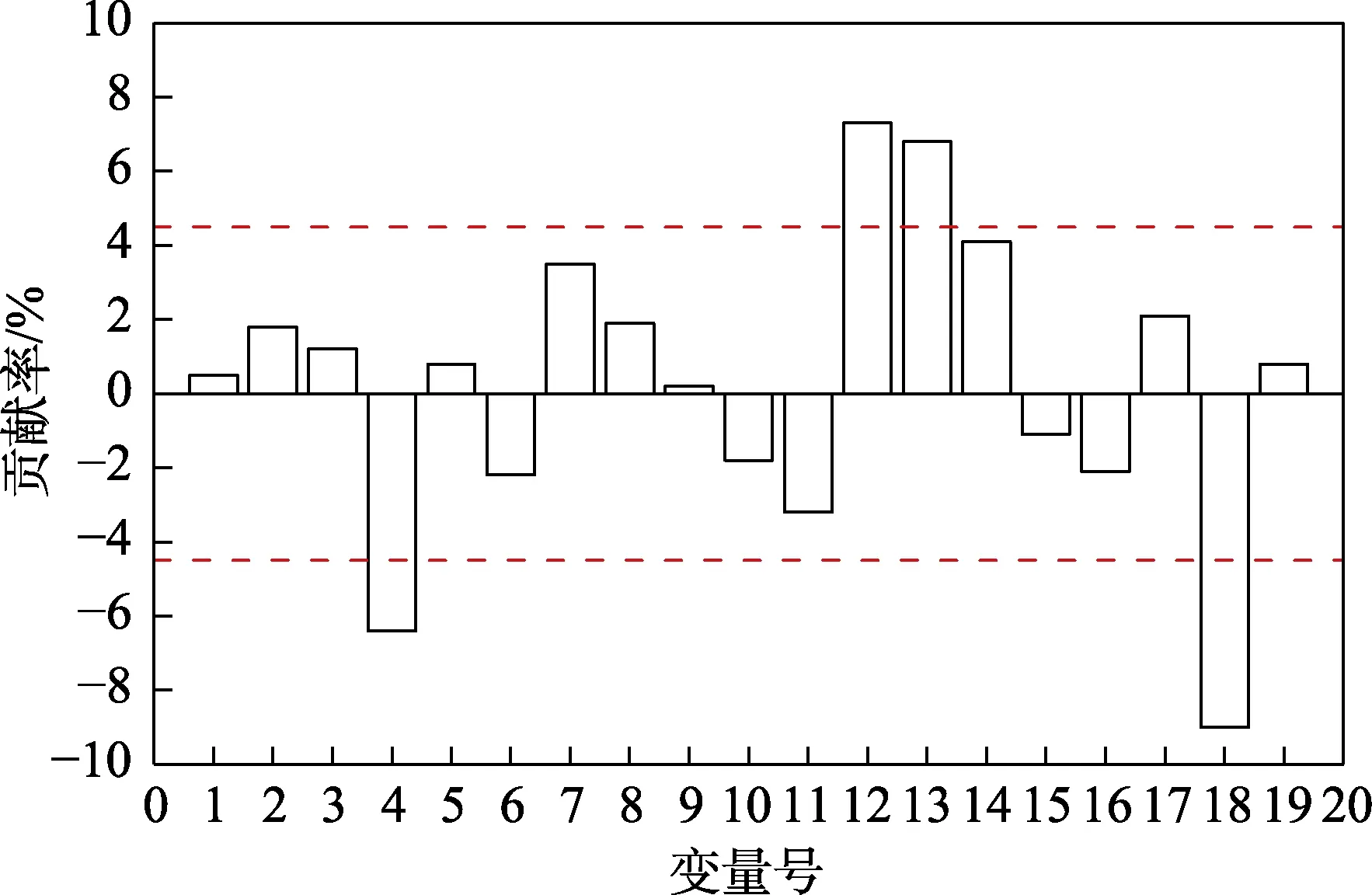
图8 变量残差贡献 Fig.8 Contribution map of variable residual

图8的横坐标代表选取的19个监测参数，从中可得出造成系统异常的主导参数有三甘醇循环量、重沸器中部温度、重沸器后端温度以及缓冲罐液位，分别对应图8的第4、12和18号参数。

诊断识别时以SDG模型下游的重沸器温度作为报警节点，该参数状态为异常偏高，反向追溯其上层节点的可能状态，其中重沸器温度调节阀开度这一节点与该报警节点呈正向连接，则推出若该阀开度为原因节点，则对应的节点符号也为“+”，但这与实际监测结果不符，从而排除这条路径；同理可排除燃料气压力异常造成重沸器温度过高这一可能性。三甘醇循环量节点与报警节点之间呈负向连接，则推出三甘醇循环量应低于正常值，与实际情况相符。类似地又从三甘醇循环量这一异常节点出发继续向上层搜索，最终得到分别以循环管路堵塞和甘醇泵故障作为根节点的两条相容通路。相比之下，甘醇泵故障所在的这条相容通路能更多地解释脱水系统中存在的异常参数，故输出诊断结果为甘醇泵故障。结合检维修记录知，该段时间内甘醇泵存在异响，柱塞频率不正常，因此诊断结果与实际情况相吻合。