基于决策树支持向量机算法的 船用设备故障诊断

唐其琯，车驰东

（上海交通大学 船舶海洋与建筑工程学院，上海 200240）

随着信息技术和互联网技术的不断快速发展，信息化、智能化的理念驱动了传统工业的发展。2015年5月，国务院正式印发了《中国制造2025》，将海洋工程装备及高技术船舶列为十个重点领域之一。同年12月，中国船级社也发布了《智能船舶规范》，对船舶数据感知、分析、评估、诊断等多个方面提出相应要求。船用设备的检修周期长，操作难度大，一旦发生故障，会影响整条船的运行。如果能及时发现故障，并进行维护修理，就能够大幅降低检修成本，为船用设备正常运行提供保障[1]。

为了增强船舶的安全性、可靠性，提高船用设备的智能化水平，需要对船舱内机械设备与系统的运行状态进行监测。基于监测数据，对设备健康状况进行评估，并为设备的检修、管理等方面决策提供支持，以满足规范中智能机舱的要求。

机械设备的故障诊断技术从20世纪60年代开始，经过半个多世纪的发展，逐渐成熟。传统的故障诊断方法主要是基于分析模型和定性经验的方法，维护周期长，且主要依赖技术人员的经验，对已有数据的利用率不高[2-3]。随着信息技术的发展，故障诊断策略逐渐向智能化过度。近年来，国内外大量研究人员对基于数据驱动的方法展开了研究，在信号处理、机器学习等方面均有所突破[4]。

在机械设备故障诊断中，常用的信号处理方法有傅里叶变换、小波变换[5]、经验模态分解（Empirical Mode Decomposition, EMD）[6-7]、正交模态分解（Variational Mode Decompositon, VMD）[8-9]等。虽然小波变换、EMD算法、VMD算法在时频域精确度等方面有更好的表现，但是传统的傅里叶变换在工程上仍然占有举足轻重的地位。大量的测试结果经快速傅里叶变换（Fast Fourier Transformation, FFT），以频谱的形式记录[10]。

在机器学习方面，支持向量机（Support Vector Machine, SVM）算法能够在小样本条件下快速训练模型。自提出以来，SVM算法被广泛应用于各类设备的故障诊断，并取得较好效果[11-13]。其他研究者的实验结果表明，支持向量机在训练时间和训练精度方面均优于神经网络[14]。

由于船用设备工况复杂，维护成本高，为了便于设备检修人员操作，更加快速、简便地实现设备状态监测及故障诊断，文中提出了一种基于振动特性的支持向量机故障诊断方法，并在实验室条件下对装有两台泵的实验台架进行多种工况测试，取得了良好的故障诊断效果，对工程实现具有一定参考价值。

1 诊断方法简介

1.1 支持向量机理论

支持向量机是一种针对小样本训练和分类的机器学习方法。以二维数据点为例，假设xoy平面内的数据点线性可分（如图1所示），为了对两类数据点进行区分，只需要找到直线wx+b=0即可。SVM算法的目标是求解能够使两类数据集正确划分，并且集合间隔最大的分界面wx+b=0，其本质是凸优化问题的求解[15-16]。

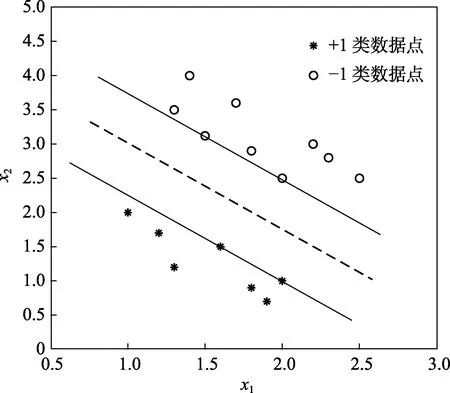
图1 二维数据点分类 Fig.1 Sketch map of two-dimensional data point classification

对于高维的特征向量，如第二节中对振动信号预处理得到的1/3倍频带谱特征向量，引入超平面的概念。基于VC维理论和结构风险最小化原则[17]，通过构造超平面，利用拉格朗日乘子法将原优化问题转化为求解拉式函数的最小值，利用SMO（Sequential Minimal Optimization）算法得到最优解，进而得到分离超平面，从而对测试数据集进行分类[18-19]。

1.2 决策二叉树方法

对于船用设备可能存在的大量不同工况、不同故障，采用二分法的思想，使用决策二叉树多分类方法进行故障诊断，提高诊断效率[20]。决策二叉树支持向量机是一种常见的多分类模型，它结合支持向量机二分类的特点，将多分类问题转化为一系列二分类问题[21-22]。以一个五分类的问题为例，如图2 所示，二叉树根节点包含了所有类别，依次对测试数据集进行分类，最终到达叶子节点，对应的类别即为测试数据对应的类别。

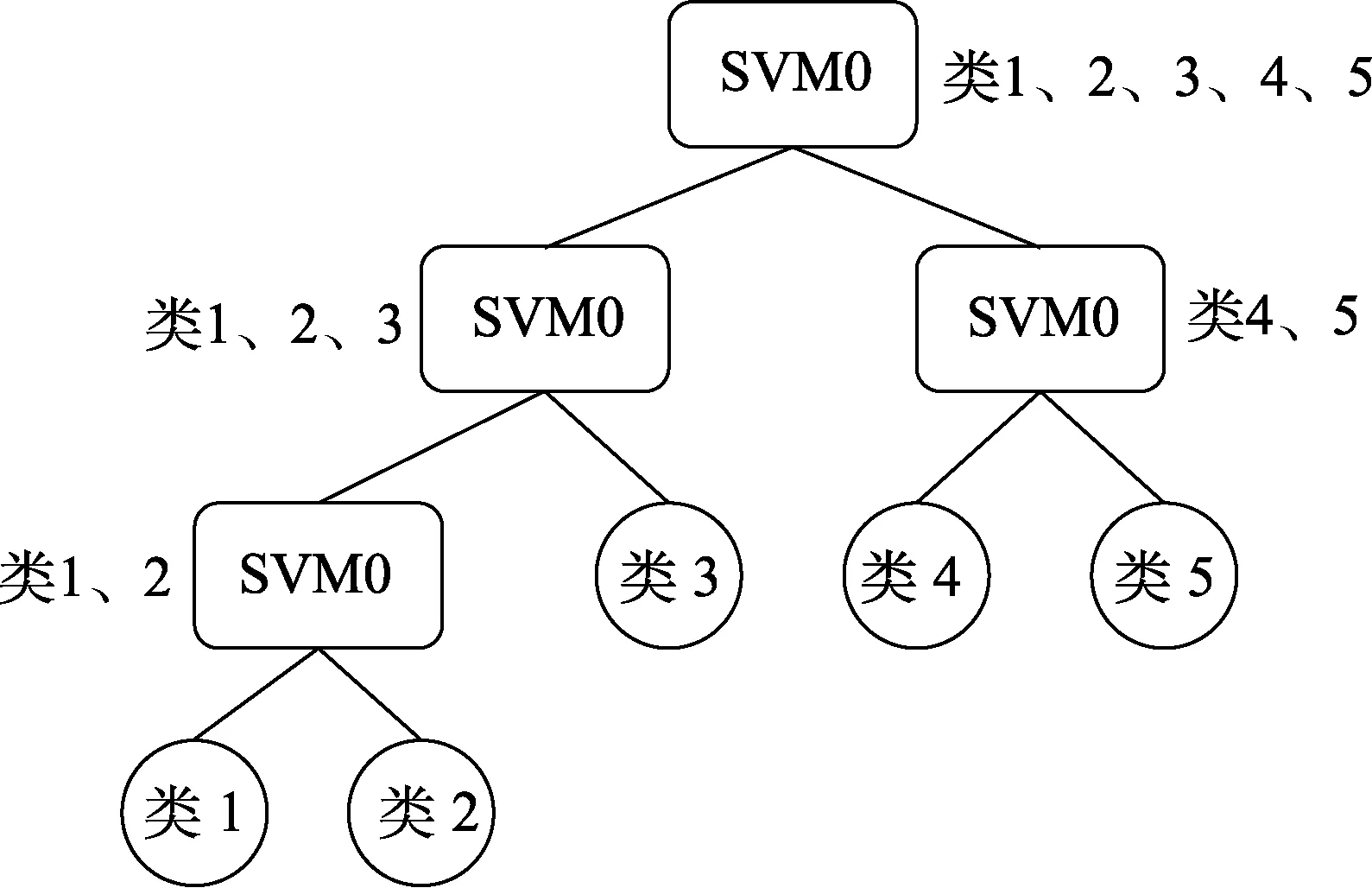
图2 决策二叉树多分类SVM树状图 Fig.2 Multi-classification SVM ketch map of decision binary tree model

1.3 诊断策略

由于船用设备存在多种工况，设备之间可能相互影响，且同一工况下可能发生多种不同故障，设备的振动特性随之发生改变。为了能够区分复杂工况下可能存在的多种故障类别，采用SVM决策二叉树方法。在模型训练时，首先对采集到的振动数据进行预处理，得到训练数据集和测试数据集。根据不同工况，划分决策树类别，训练得到SVM树模型，作为测试数据集的分类依据。具体操作流程如图3所示。

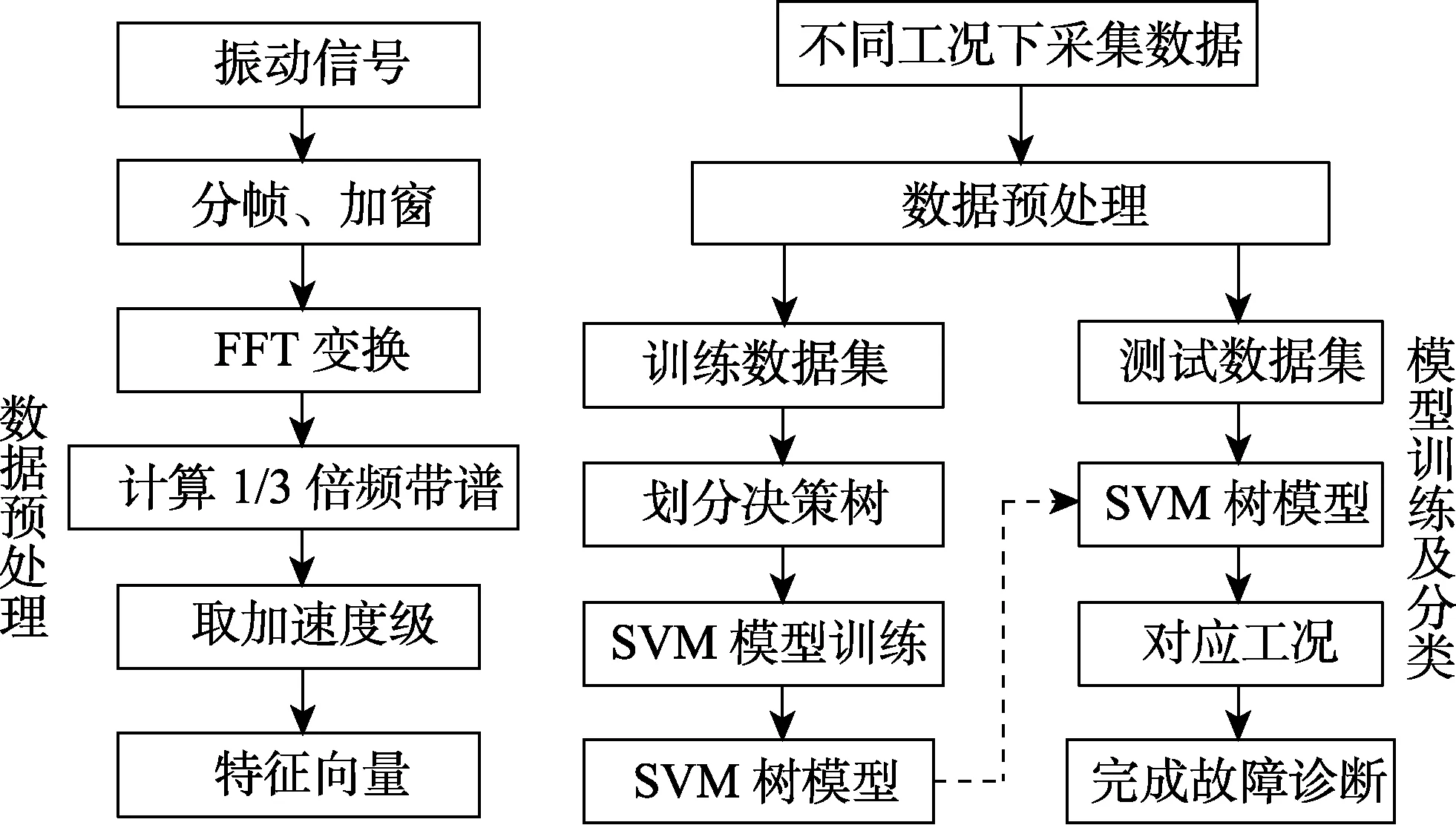
图3 数据处理及分类流程 Fig.3 Flow chart of data processing and classification

2 故障诊断实验

为了验证上述故障诊断策略的可行性，在实验室条件下模拟机械设备在船舱内的工况，采集振动数据，并进行模型训练及分类。测试采用SVM树模型进行故障分类的准确率，并探究不同传感器布置对故障诊断准确率的影响。

2.1 实验台架及测试工况

测试对象为两套工作泵组，分别通过管路与油柜连接构成回路。泵组和油柜均布置于一个模拟舱段结构上，舱段底部通过隔振系统与地基连接，整个系统的安装频率为1 Hz左右，以模拟海上漂浮状态。数据采集系统通过加速度传感器采集并记录测试对象的振动信号，然后传输至计算机进行分析。实验台架如图4—6所示。

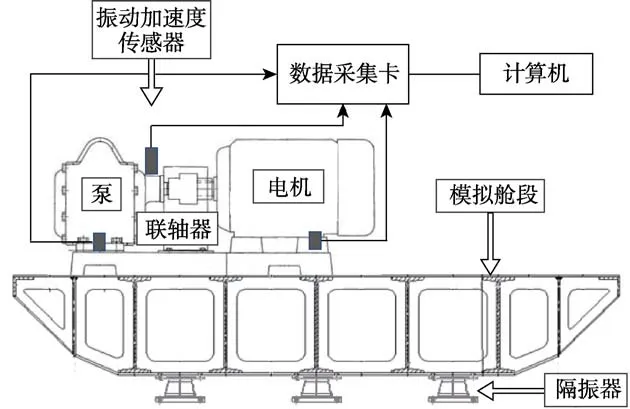
图4 试验台架整体 Fig.4 The overall diagram of the experimental bench

为了探究不同传感器布置对模型训练及故障识别准确率的影响，在泵体、底座及联轴器等位置沿不同方向共布置有6个加速度计，测点信息详见表1。

表1 传感器布置 Tab.1 Sensor arrangement

本次实验共设定两个工况：单独工作和两台泵共同工作，分别进行测试。在单独工作时，模拟以下几 种故障：泵底部螺栓松动、电机底部螺栓松动、电机和泵底部螺栓均松动及正常状态，见表2。

表2 实验工况 Tab.2 Experimental working conditions

图5 联轴器端传感器布置 Fig.5 Sensor layout at the coupling

图6 辅机设备整体构造 Fig.6 Overall structure of the auxiliary equipment

2.2 数据处理及分析

2.2.1 信号特征提取

在故障诊断中，既要求所选取的参数特征明显，又要考虑数据的规模。文中主要提取振动信号的1/3倍频带特征，对传感器采集到的振动信号进行预处理。选取原始信号中的平稳信号，以覆盖率80%、帧长0.8 s截取若干数据段，使用hamming窗对每段数据进行加窗变换，再做快速傅里叶变换。将50 Hz设定为第一个中心频率，2500 Hz为最后一个中心频率，计算得到1/3倍频带谱，并用加速度级表示。每段数据得到18个倍频带谱分量，组成一个特征向量作为后续模型训练及分类的输入。

2.2.2 数据处理及模型训练

在振动时域信号中截取一段稳态信号，按覆盖率80%、帧长0.8 s分帧，并通过FFT转化为中心频率从50~2500 Hz的1/3倍频带频谱。以测点1数据为例，图7a、8a、9a图所示为截取的三个工况下的时间信号，图7b、8b、9b为平均后的1/3倍频带数据，将频带数据转化为向量，即为所需特征向量。

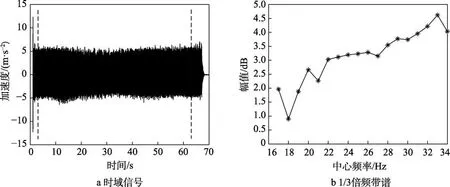
图7 测点CH1在01工况下的时域信号及1/3倍频带谱 Fig.7 (a) Time domain signal and (b) one-third octave spectrum of measuring point CH1 under working condition 01

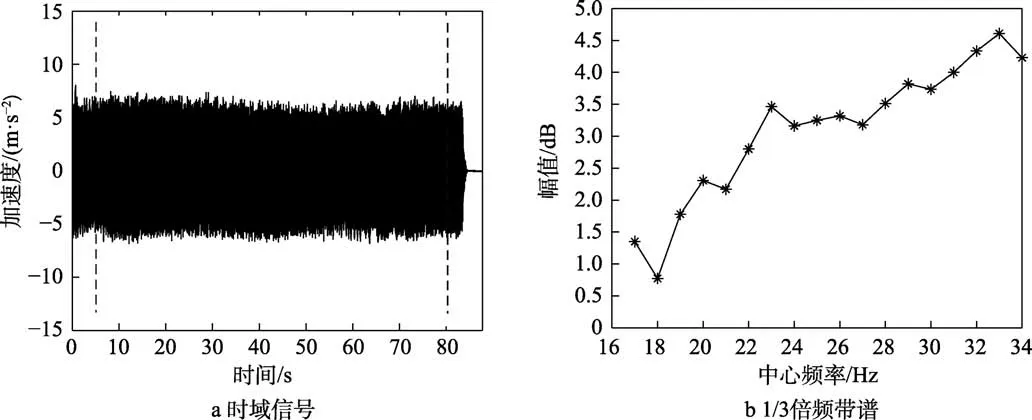
图8 测点CH1在02工况下的时域信号及1/3倍频带谱 Fig.8 (a) Time domain signal and (b) one-third octave spectrum of measuring point CH1 under working condition 02

三帧数据对应的特征向量分别为：

将每一个工况下分帧得到的多个数据点随机分为两部分，其中一部分作为训练数据集，用于SVM模型训练；另一部分作为测试数据集，验证故障诊断策略的可行性。

根据实验设置的工况，按图2所示进行二叉树划分，分别训练得到SVM0-3，构成SVM树模型。为了探究不同测点的传感器布置对故障诊断准确率的影响，分别处理6个通道的数据，并分别测试得 到结果。

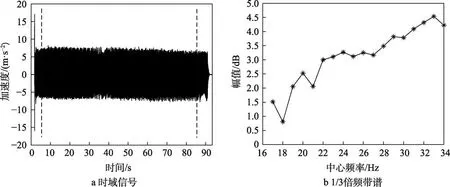
图9 测点CH1在03工况下的时域信号及1/3倍频带谱 Fig.9 (a) Time domain signal and (b) one-third octave spectrum of measuring point CH1 under working condition 03

2.2.3 分类结果

为了更直观地展示分类结果，采用PCA（Principle Component Analysis）算法对数据集进行降维，选取权重最大的三个特征维度进行可视化[12]。提取中心频率400、800、1000 Hz的1/3倍频带谱幅值为三个维度，绘制CH1通道在5种工况下的20个数据点，如图10所示。

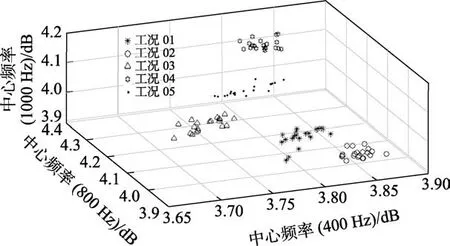
图10 5种不同工况特征分布 Fig.10 Distribution of characteristic values of five different working conditions

不难发现，在选取的三维数据特征下，3种不同工况对应的数据点是线性可分的。通常认为，数据特征维数越高，线性可分的概率越大，而文中选取的1/3倍频带谱具有18个维度的特征值，以此推断采用1/3倍频带谱作为输入大概能满足支持向量机分类。从频谱分析的角度而言，不同故障对应的频域峰值不同，从而引起某一维度的特征变化，并以此进行分类。

将测试数据集依次输入分类器，根据分类情况，推断测试集所属的故障工况，6个测点对应的测试结果见表3。CH1、CH2、CH4、CH5的分类正确率均为100%，CH3、CH6的分类正确率分别为88.4%、85.6%，总体识别准确率较高。考虑到CH3、CH6分别对应联轴器端的垂向、横向测点，而其他测点均位于设备基座上。由此可见，对基于振动信号的故障诊断，测点布置的方向对识别结果影响较小，但识别精度随测点与故障点距离的增大而减小，该结论有利于指导针对特定故障的传感器布置。

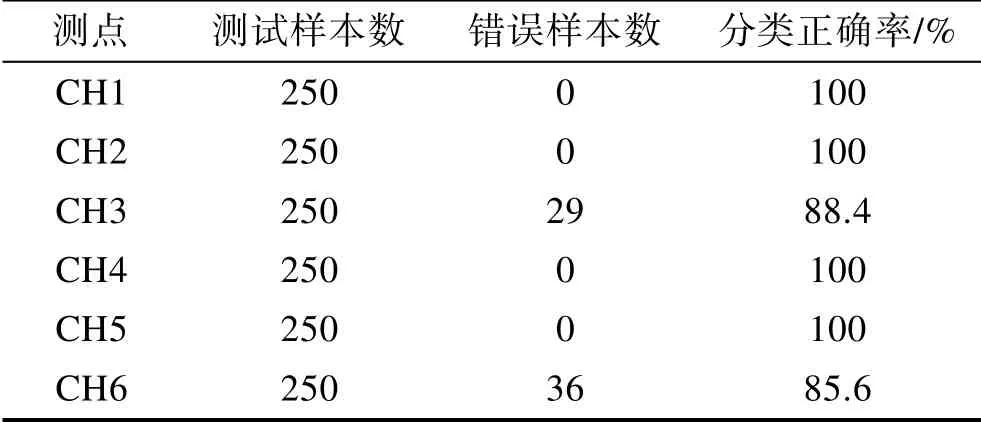
表3 实测数据分类结果 Tab.3 Experimental results of measured data

3 结论

文中提出了一种基于倍频带谱和支持向量机的船用辅机故障诊断策略。对传感器采集到的振动信号进行频谱分析，提取每一段信号的1/3倍频带谱作为特征向量。利用支持向量机训练模型，并对测试数据进行分类。通过实际船用设备测试可见，以1/3倍频带数据作为支持向量的决策树模型，对故障点附近的测点具有较高的识别精度，错误率会随测点距离增大而增大，但测点方向对识别精度几乎无影响。该方法对船用设备状态监控、故障诊断、健康评估及相应的传感器布置方案等均提供了支持。