数据匿名化对群体间差异的统计表征的影响 *
2021-10-12许衡张楠/文顾洁/
许 衡 张 楠 /文 顾 洁 / 译
一、引 言
近年来,以欧盟《通用数据保护条例》(GDPR)为代表的隐私保护法规接连出台,刺激了数据匿名化技术的扩散。一般来说,数据匿名化技术是作为组织或群体层面的解决方案被概念化,进而进行相应的技术开发的,其目的是用来平衡两种对立的利益:一是为了保护隐私,使数据与数据主体(即个人)脱离关联;二是保持数据的实用性。例如,苹果公司在收集iOS设备中的用户键盘输入时,部署了差分隐私技术。一方面,收集到的输入内容不再能轻易地关联到个人;而另一方面,苹果仍然可以利用收集到的数据来改进其自动纠正和预测性文本输入功能。由于将数据与数据主体脱离关联会降低数据的实用性,1Daniel Kifer and Ashwin Machanavajjhala, No Free Lunch in Data Privacy, Proceedings of the 2011 ACM SIGMOD International Conference on Management of Data, 2011, pp. 193-204.2Cynthia Dwork, Frank McSherry, Kobbi Nissim and Adam Smith, Calibrating Noise to Sensitivity in Private Data Analysis, Journal of Privacy and Confidentiality, vol. 7, no. 3, 2016, pp. 17-51.许多数据匿名化技术将隐私与实用性的权衡操作为一个可调整的参数,在组织层面进行设置。
将数据匿名化作为组织层面的解决方案予以实施符合监管要求,但可能不满足个人隐私偏好的特异性。3Alessandro Acquisti, Laura Brandimarte and George Loewenstein, Privacy and Human Behavior in The Age of Information, Science, vol. 347, no. 6221, 2015, pp. 509-514.同样,提升(或降低)数据实用性所带来的好处(或危害)也会具有很大的个体差异。4Evaggelia Pitoura, Panayiotis Tsaparas, Giorgos Flouris, Irini Fundulaki, Panagiotis Papadakos, Serge Abiteboul and Gerhard Weikum, On Measuring Bias in Online Information, ACM SIGMOD Record, vol. 46, no. 4, 2018, pp. 16-21.将组织层面的解决方案和个人层面的影响结合起来考虑,自然会出现一个问题:组织层面一刀切的隐私保护解决方案是否会对不同个体产生差异化的影响?对这一问题的回答具有政策意义,因为如果差异化的影响确实存在,立法者和监管者就需要对不同数据收集主体个性化隐私保护能力的强弱进行甄别。
遗憾的是,现有关于数据匿名化影响的研究主要集中整体数据效用的降低上,这也是在组织层面对所有数据记录进行计算的结果。然而,数据匿名化在个人层面是否会产生差异化的影响尚未有定论。回答这个问题显然是具有挑战性的。首先,数据匿名化的设计和匿名数据的使用通常受专有技术和流程的约束,对研究者和公众来说是不透明的。其次,数据匿名化对个人的影响也很难处理,因为即使是隐私专家也经常对数据匿名化技术在隐私保护方面的作用感到困惑。5Jane Bambauer, Krishnamurty Muralidhar and Rathindra Sarathy, Fool’s Gold: An Illustrated Critique of Differential Privacy, Vanderbilt Journal of Entertainment & Technology Law, vol. 16, 2013, p. 701.为了回答这个问题,我们将重点放在对一种具备可分析性,同时具有实践意义的特定类型的差异的分析上,即:数据匿名化是否可以掩盖数据集中人群之间的统计差异。如果数据匿名化掩盖了群体间差异,则可能会对商业、社会和政策产生深远的影响。例如,它可能会造成苹果公司无法为具有独特语言模式的少数族群提供准确的输入检测和自动纠正功能。在医疗保健背景下,可能会导致与性别、种族、民族、收入、性取向等人口属性有关的健康差异无法识别,而健康差异代表了美国面临的最紧迫的社会公正问题之一。6Ed Kelley, Ernest Moy, Daniel Stryer, Helen Burstin and Carolyn Clancy, The National Healthcare Quality and Disparities Reports: An Overview, Medical Care, vol. 43, 2005, pp. I3-I8.对于美国人口普查来说,如何应用数据匿名化技术引起了广泛的公共讨论,7Michael Macagnone, Efforts to Safeguard Census Data could Muddy Federal Data, https://www.govtech.com/analytics/Efforts-to-Safeguard-Census-Data-Could-Muddy-Federal-Data.html.对群体差异的掩盖可能对未来十年的公共政策产生不利影响。
为了研究数据匿名化技术对统计差异检测的潜在影响,必须首先确定当前技术对私人数据进行匿名化的机制,并界定用以识别亚人群之间差异所需的统计证据。我们首先将数据匿名化的机制归类为数据移除(data removal)或噪声插入(noise insertion),同时将统计差异操作化为隔离差异(disparity through separation)或变差差异(disparity through variation)。在对这两类概念进行详细介绍后,我们探讨了两者之间的相互作用,即每种匿名化机制(数据移除vs.噪声插入)对每种统计差异(隔离差异vs.变差差异)的影响。这四种(2 *2)组合会产生不同结果:对于隔离差异,噪声插入机制倾向于掩盖差异的存在,但与掩盖差异相比,数据移除机制更容易造成假阳性的结果;相反,对于变差差异,两种数据匿名化机制都既可能掩盖差异,又造成假阳性,甚至在一些情况下会倒转群体间差异的方向。我们通过概念构建和数学形式进行论证,然后用经验证据进行验证。本文的最后一节讨论了我们的发现的实际意义,我们工作的局限性,以及未来研究的潜在方向。
二、概念构建
(一)数据匿名化的类型:数据移除与噪声插入
1.数据移除。由于数据匿名化的目标是防止任何个人从匿名数据集中被识别出来,所以对数据集进行匿名化的一个自然构想就是删除数据中可能被用来识别个体的部分,数据移除机制就植根于这个想法。最初,数据移除是通过删除那些明显的标识符变量,如姓名、地址、社会安全号等。但这一做法很快受到挑战——研究发现,87%的美国人可以通过邮政编码、性别和出生日期的组合来进行唯一识别,而这些变量都不是传统意义上的“标识符”。1Sweeney Latanya, Simple Demographics Often Identify People Uniquely, Health, vol. 671, 2000, pp. 1-34.在这一突破性的发现之后,计算机科学文献中开发了大量的数据移除技术,用以检测和纠正这种“准标识符”造成的问题。2Sweeney Latanya, K-anonymity: A Model for Protecting Privacy, International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, vol. 10, no. 5, 2002, pp. 557-570.3Ashwin Machanavajjhala, Daniel Kifer, Johannes Gehrke and Muthuramakrishnan Venkitasubramaniam, l-Diversity:Privacy beyond K-anonymity, ACM Transactions on Knowledge Discovery from Data (TKDD), vol. 1, no. 1, 2007, pp. 1-52.
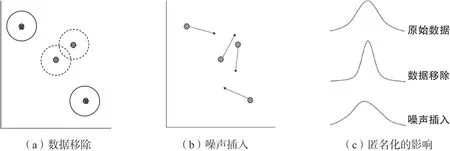
图1. 数据匿名化机制
虽然这些技术在设计上存在很大的不同,但它们遵循的共同程序是首先确定哪些个人有被识别的风险,然后再删除去识别化所需的最低信息量。图1(a)展示了一个简单的例子:如果一个人在数据集中的记录与其他个体的记录有较大差别,那么他/她就有被识别的风险(即图中实线框所显示的个体数据记录附近存在一个空邻域)。如图中所示,对数据集进行匿名化的逻辑就是删除附近存在空邻域的记录。除了这个简单的例子之外,还开发了许多其他形式的数据移除,例如删除个人的选定变量或用更粗粒度的值来替代原有变量,例如,通过将邮政编码改为城市或州。
关于数据移除的技术研究几乎在2010年左右就停止了。部分原因是我们接下来将讨论的噪声插入机制的出现。然而,更重要的原因是多源数据融合造成了数据移除机制的有效性降低:研究人员意识到,如果无法对哪些其他数据源可能与匿名数据集联系起来做出实质性假设,就无法限制对个人身份的识别。1Ganta Srivatsava Ranjit, Shiva Prasad Kasiviswanathan and Adam Smith, Composition Attacks and Auxiliary Information in Data Privacy, Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2008, pp. 265-273.有趣的是,这种担心并没有阻止数据移除在实践中的运用。时至今日,数据移除不仅被企业和政府机构广泛采用,而且经常被列为遵守隐私法律法规的推荐做法。表1描述了得克萨斯州卫生服务部(2019年)所用的数据移除规则,其目的是对全州范围内的住院病人出院数据集进行匿名化操作,以符合相关法规的要求。纽约等许多其他州也采用了类似的规则。

表1. 得克萨斯州卫生保健信息收集匿名规则
2.噪声插入。早期关于噪声插入的工作囿于简单地将独立的高斯噪声添加到数据集中的所有变量中,插入的噪声可以使用光谱滤波技术(spectral filtering technique)从匿名数据中隔离出来,2Huang Zhengli, Wenliang Du and Biao Chen, Deriving Private Information from Randomized Data, Proceedings of The 2005 ACM SIGMOD International Conference on Management of Data, 2005, pp. 37-48.从而有效地重新启用个人身份识别。差分隐私的发展解决了这一问题,并以统计学上的不可区分性的形式在包含个人信息的数据集和不包含个人信息的数据集之间提供了严格的匿名性保证。更重要的是,无论有什么其他数据源可以与匿名数据相联系,使用差分隐私技术的匿名性保证都是成立的。差异隐私避免了数据移除的技术陷阱,已经成为噪声插入技术的事实标准,帮助噪声插入在数据匿名化研究中获得广泛的认可,同时也在实践中被高科技公司和美国人口普查局等机构被广泛应用。
广泛意义上的噪声插入方法与具体的差分隐私技术都有很多不同的类别和形式。随机噪声可以如图1(b)所示直接添加到原始数据中,3Agrawal Rakesh and Ramakrishnan Srikant, Privacy-preserving Data Mining, Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, 2000, pp. 439-450.4John Leslie K., George Loewenstein, Alessandro Acquisti and Joachim Vosgerau, When and Why Randomized Response Techniques (Fail To) Elicit The Truth, Organizational Behavior and Human Decision Processes, vol. 148, 2018, pp.101-123.或者在回答数据查询命令时添加到数据集上。5Cynthia Dwork, Frank McSherry, Kobbi Nissim and Adam Smith, Calibrating Noise to Sensitivity in Private Data Analysis, Journal of Privacy and Confidentiality, vol. 7, no. 3, 2016, pp. 17-51.噪声插入后的统计估计可以保持无偏见(例如用标准的拉普拉斯机制进行差分隐私),或者包括由输入数据决定的微小偏差(例如数据和工作量感知算法进行差分隐私)。同样,插入的噪声可以独立于原始数据集或根据原始数据生成。虽然实现方式不同,但它们的概念基础是非常一致的:从匿名数据推断出的任何统计数据的置信区间必须比对原始数据集的推断更宽,从而无法根据统计推断区分个人是否在原始数据集中。
图1(c)对两种匿名机制进行了比较。数据移除通常会给估计的统计数据带来偏差,并可能降低观察到的标准差,其原因是这种方法倾向于删除“离群”记录,如图1(a)中的空邻居记录。相比之下,噪声插入技术通常是无偏的,或者对估计的统计数据引入最小的偏差。尽管如此,插入的噪声往往会大大增加观察到的标准差。
(二)差异的类型:隔离差异与变差差异
从社会学和犯罪学到流行病学和医学等各种学科中,对群体间差异的检测是一个长期存在的研究问题。考虑到研究这个问题的领域范围,我们并不试图在我们对群体差异的分类做到详尽无遗。相反,进行如上分类的目的是强调两种概念上不同但同样普遍的差异操作类型——一旦应用数据匿名化,这两种类型的差异操作化就会呈现不同的结果。表2总结了隔离差异和变差差异操作方式的主要区别。接下来,我们首先分别描述这两种类型,然后再阐释两者之间的差异。
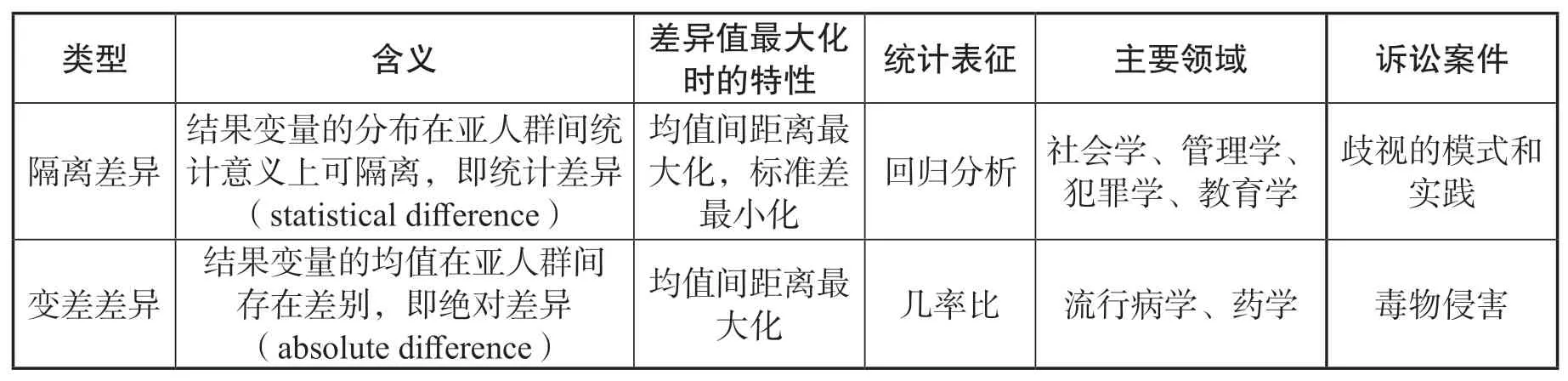
表2. 差异操作化的含义和属性
隔离差异:起源于社会学中对种族歧视的研究,并自然而然地扩展到与就业歧视有关的领域以及与劳动力市场有关的法院案件,例如指控工作场所系统性歧视的模式和做法的案件。在这些领域,识别差异背后的主要目的是确认或拒绝存在基于种族或性别等重点社会决定因素的潜在歧视。从指示性的角度看,差异的操作是为了从偶然性中辨别其存在。例如,法院在确定歧视案件的初步证据时,长期以来一直采用5%的显著性门槛,这意味着所观察到的差异必须有小于5%的概率是偶然造成的。最高法院在Castaneda V. Partida一案中,将5%的门槛转化为观察到的差距,认为差距必须超过“两个或三个标准差”。从本质上讲,这与研究人员通过样本均值比较来检测差距的操作方法相同——尽管研究中的操作方法往往更为复杂,不仅要考虑到重点社会决定因素,还要考虑到其他相关变量以及社会决定因素与其他变量之间的互动效应。
我们将这种对差异的操作化称为“隔离差异”,因为在研究和法律领域,这些操作化的基础是检测不同亚人群的结果分布之间的隔离。考虑图2中描述的一个简单的例子,其中有两个子群体,结果变量是二进制的,例如,代表员工是否被晋升到管理职位。假设不同员工的晋升决策之间是独立的,那么每个子人群中被晋升的员工比例形成二项分布。从图中可以看出,当群体差异通过隔离来衡量时,其检测取决于不同子群体的晋升率分布之间的隔离程度,而不是观察到的晋升率之间的原始差异。例如,当数据集中每个子人群有10个样本时,当观察到的晋升率分别为30%和70%时,推算出的差异不能满足5%的阈值(t=1.95,双尾t检验的p=0.067)。然而,当样本量较大时,对于更接近的一对观察到的晋升率,如40%和60%,差距却可以达到阈值(例如,当n = 50时,有t = 2.04,p < 0.05)。表2中总结的这一特性的含义是,当各子群体之间结果变量的平均距离最大化,每个子群体内的结果变量的标准差最小化时,就会出现最大的隔离差异。我们将在后文中讨论当群体间差异通过隔离操作时,数据匿名机制如何通过影响结果变量的均值和标准差,进而影响群体间差异的统计检测。
变差差异:差异的另一种操作方式起源于流行病学,进而被扩展至各领域,其实践应用包括对收入差异的检测、法院侵权案件的论证等。一个典型的例子是Daubert v. Merrell Dow 药物案,该案中,统计证据被用来确定在怀孕期间摄入某种药物是否对出生缺陷有不同的影响,即服用该药物的人和没有服用该药物的人之间是否存在出生缺陷率的差异。在这些领域,对差异进行操作的目的往往不仅是为了确定其存在,而且是为了量化其程度。值得注意的是,通过结果变量的变化对变差差异进行测度是为了衡量差异的程度而设计的。例如,长期以来,法院在民事案件中对建立差异影响适用了“几率比”(odds ratio)的要求,这意味着在一个群体中出现不希望的结果的几率必须是另一群体几率的至少两倍。1Gastwirth Joseph L, The Role of Statistical Evidence in Civil Cases, Annual Review of Statistics and Its Application,vol. 7, 2020, pp. 39-60.这种相对比率类似于流行病学研究中用于检测差异性的赔率指标。2Hebert Paul L., Jane E. Sisk and Elizabeth A. Howell, When Does a Difference Become a Disparity? Conceptualizing Racial and Ethnic Disparities in Health, Health Affairs, vol. 27, no. 2, 2008, pp. 374-382.
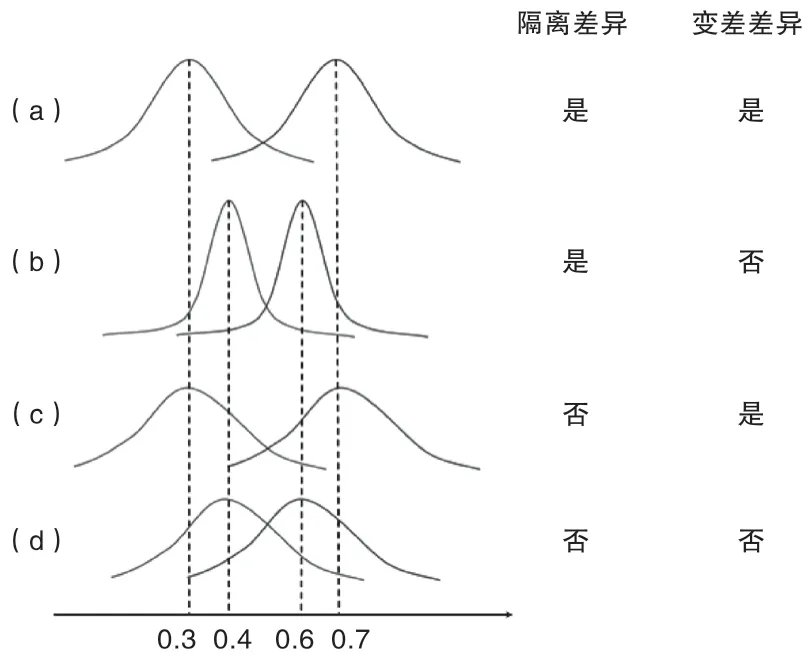
图2. 不同差异操作化的图解说明
我们将上述这种对群体差异的操作称为“变差差异”。在研究和法律领域,这种对差异进行操作化的基础是将不同亚人群的平均结果进行对比。再来看看图2中的例子。当差异通过变差进行计算时,其检测只取决于观察到的晋升率,而不是它们分布的标准差。例如,观察到的一对30%和70%的晋升率总是符合“多半可能”的标准(more likely than not,因为0.7=0.3>2),无论从统计意义上这种差异是否满足上述5%的阈值标准。相反,如果观察到的比率是40%和60%,无论样本有多大,两个分布是否重叠,它们的比率都低于临界点(0.6=0.4=1.5<2)。如表2所总结的,当通过变差来操作群体间差异时,当平均结果之间的距离达到最大时,就会出现最大的差异。变差差异的计算与每个子群体内结果的标准差无关,这与通过隔离来计算差异形成了鲜明的对比。
同时还要注意到,当数据没有匿名时,只要样本量足够大,忽略样本标准差不会造成研究结论的不可靠。此外,由于变差差异的分布(如几率比)倾向于正偏态,意外掩盖现有群体间差距的可能性相当小。然而,正如我们将在数学形式主义部分所阐述的,一旦数据集被匿名化,情况就会发生巨大的变化。例如,无论样本大小,许多噪声插入算法都会给统计估计引入不确定性。1Cynthia Dwork, Frank McSherry, Kobbi Nissim and Adam Smith, Calibrating Noise to Sensitivity in Private Data Analysis, Journal of Privacy and Confidentiality, vol. 7, no. 3, 2016, pp. 17-51.在这种情况下,即使是大样本也无法消弭标准误在差异检测中的作用。这一特点导致了数据匿名化对两种差异操作的不同影响。
(三)数据匿名化对差异检测的影响
在介绍数据匿名机制的类型时,我们概述了数据移除和噪声插入之间的两个重要区别。首先,数据移除通常会降低结果变量的标准差,而噪声插入几乎总是增加标准差。其次,数据移除技术很少对从匿名数据中估计的统计数据的偏差做出保证,与之相对,许多噪声插入技术能够确保某些估计的统计数据(例如,平均值)是无偏差的。在接下来的内容中,我们将讨论这两种区别是如何与两种差异操作化相互作用,造成对匿名数据进行差异检测的不同结果。表3总结了主要的差异。

表 3. 数据匿名化对差异操作的影响
关于隔离差异,鉴于数据移除和噪声插入倾向于将标准差向相反的方向移动,我们可以预期它们对隔离差异的检测也会有不同的影响。例如,噪声插入极有可能掩盖隔离差异,因为标准差的增加降低了子群体之间差异的显著性水平。出于同样的原因,当原始数据集中不存在差异时,噪声插入造成假阳性错误的可能性极小。相比之下,数据移除技术降低了观察到标准差,因此更容易引发隔离差异检测的假阳性错误。同样地,除非数据移除减少子群体之间的观测差异,否则该方法不太可能引发隔离差异检测的假阴性错误。
关于变差差异,标准差的变化并不影响变差差异的计算,但观察到的结果变量的偏差却会产生影响。这就凸显了数据移除技术引入的潜在偏差。图3描述了这样一个例子。从图中可以看出,在原始数据集中,两个子群体的平均结果是相同的。然而在移除部分数据后,一个子群体的平均结果变成了另一个子群体的两倍,产生了假阳性错误。同样可以构建相反的情况,即数据移除掩盖了现有的差异。因此,在数据移除机制下,偏差是表现为假阳性还是假阴性,很大程度上取决于基础数据分布。这与噪声插入的情况形成鲜明对比。大多数现有的噪声插入技术保证了平均估计值的绝对或渐进无偏性。1Cynthia Dwork, Frank McSherry, Kobbi Nissim and Adam Smith, Calibrating Noise to Sensitivity in Private Data Analysis, Journal of Privacy and Confidentiality, vol. 7, no. 3, 2016, pp. 17-51.虽然标准差的增加仍可能使观察到的比率向不可预测的方向转变,但无论基础数据分布如何,我们观察到假阳性和假阴性的几率大致相同。

图3. 数据移除造成假阳性的图示
三、数学表达
(一)前期工作
数据模型:探索群体差异的一种常用方法是构建回归模型。例如要研究不同种族的员工获得晋升机会时是否存在种族间的差异,一般将观测到的结果变量(例如工作场合的晋升)作为被解释变量Yi,将核心的社会决定因素Zi(例如种族)和其他相关的观测特征Xi(例如工作表现,Xi可包含多个变量)作为解释变量构建回归方程。εi为误差项(均值为0)。一个简化的模型是将β2设为0,即只关注社会决定因素Zi的直接效应,而不包含Zi与其他因素Xi的交互效应。该模型也可通过对数变换研究非线性关系。

差异操作化:群体间差异可以简单地通过公式(1)中的β2Xi+β3表示,该值可以表征给定个体特征Xi的情况下群体间在结果变量Yi的差异。例如,当社会决定因素Zi是0/1变量时,β2Xi+β3是当个体从一个子群体(Zi=0)转向另一个子群体(Zi=1)时,结果变量Yi值的差距。与这一解释相一致,子群体间的平均差异可以表示为β2Xu+β3,其中Xu为子群体在观测特征Xi上的平均值。当β2=0时,群体间的差异为β3。
匿名机制:图4说明了两种匿名机制的设计。对于这两种机制,匿名化的输入是数据集中所有变量的集合,即模型中的(Xi,Yi,Zi)。对于数据移除机制,其目标是防止从输出数据中识别出一个独立个体。现有技术有两种常用的方法来实现这个目标。一种是对某些变量的值进行泛化。例如,在图4(a)中,我们将前两条记录的Yi的值从28和32都替换为30。通过这样做,我们使这两条记录彼此相同,因此从输出数据中无法唯一识别。第二种方法叫做抑制,即删除那些不容易与其他记录相似的记录。图4(a)中的最后一条记录就是一个例子。鉴于其Yi的值与其他记录相差甚远,在泛化方法下为了使最后一条记录与其他任何记录相同,必须对两条记录的Yi进行重大改变,其结果是限制了两者在匿名数据中的有用性。与泛化方法相反,我们可以简单地从匿名化数据中删除最后一条记录,并保存其他记录不被修改,就像图4(a)所示。请注意,图中的匿名化数据符合一种流行的数据删除保证,称为k-匿名性(k = 2),它要求对于匿名化数据集中的每一条记录,必须有至少k-1条具有完全相同值组合的其他记录。1Sweeney Latanya, K-anonymity: A Model for Protecting Privacy, International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, vol. 10, no. 5, 2002, pp. 557-570.
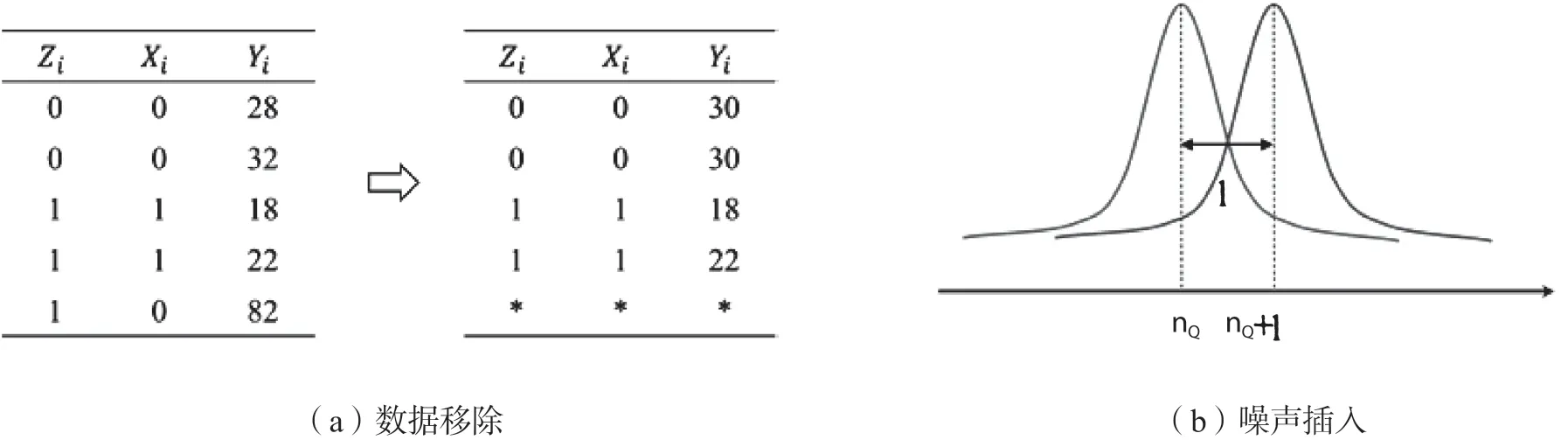
图4. 数据匿名化机制的图示
与数据移除相比,现有的噪声插入技术已经提供了对数据集或查询结果产生随机扰动的更灵活的输出方式。相应地,噪声插入机制的匿名性保证,就像前面提到的差分隐私保证一样,被广泛地设想为支持任何将输入数据集映射到任意范围的噪声插入算法M。例如,流行的(ϵ,δ)差分隐私保证要求,对于任何两个相差一条记录的数据集D和D',以及任何S Θ,M(D)∈S和M(D',)∈S的概率不能有显著差异,差异由两个参数ϵ和δ的函数进行约束。
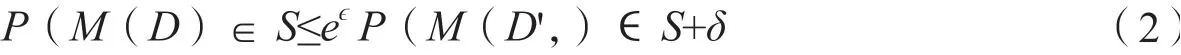
在上述公式中,(ϵ,δ)的值越小,在施加函数M后越难将D和D',进行区分,这意味着函数M提供了更严格的匿名化保证。
研究人员已经开发了许多可以保证(ϵ,δ)差异隐私的技术。1Hay Michael, Ashwin Machanavajjhala, Gerome Miklau, Yan Chen and Dan Zhang, Principled Evaluation of Differentially Private Algorithms Using Dpbench, Proceedings of the 2016 International Conference on Management of Data,2016, pp. 139-154.一个简单而又流行的是图4(b)中描绘的拉普拉斯机制,2Cynthia Dwork, Frank McSherry, Kobbi Nissim and Adam Smith, Calibrating Noise to Sensitivity in Private Data Analysis, Journal of Privacy and Confidentiality, vol. 7, no. 3, 2016, pp. 17-51.它在回应数据查询命令时插入噪声。例如,当回答一个要求满足Q条件的记录数nQ的计数查询时,拉普拉斯机制会在nQ中加入一个从拉普拉斯分布中抽取的、均值为0、尺度参数为1/ε的随机变量,因此,在点nQ+r处查询的概率密度是:

图4(b)中的曲线画出了该概率密度函数。从等式3中注意到,当nQ变化为1时,概率密度以倍数系数e-ε变化,即两个数据集D和D',之间相差一条记录的最大可能差值(如差分隐私定义中规定的)。根据公式2,这意味着无论数据集D或查询Q是什么,拉普拉斯机制总是能实现(ϵ,δ)-差分隐私。
(二)匿名化机制对差异检测的影响
我们首先考虑数据移除机制如何影响差异检验的结果。当群体间的差异通过隔离差异来操作时,估计的回归系数的标准误差显著影响了检验统计学意义上群体间的隔离差异。因此,下面的定理研究了数据移除的泛化方法——专门为实现上述k-匿名性保证而设计——如何影响回归输出的标准误差。请注意,该定理假设在回归分析中直接使用匿名数据集,这也是目前这些数据集在实践中的使用方式。3Luc Rocher, Julien M. Hendrickx and Yves-Alexandre De Montjoye, Estimating the Success of Re-Identifications in Incomplete Datasets Using Generative Models, Nature communications, vol. 10, no. 1, 2019, pp. 1-9.虽然可以修改回归分析以补偿数据移除的影响,但这种专用算法的设计超出了本文的范围。
定理1:当数据集中Xi和Zi的每个值的组合有k条记录时,则用每个匿名组中Yi的平均值替代Yi的具体的值,以此来实现匿名化。匿名化后每个回归系数(即β0、β1、β2、β3)估计值的标准误差减少了的倍数系数。
与我们之前的概念推演结果一致,定理1表明,使用数据移除机制,特别是流行的泛化技术,会降低回归系数的标准误差,并可能在识别差异时产生假阳性。虽然数学证明很微妙,但该定理的发现有一个简单直观的解释。请注意,一般的数据移除,特别是泛化,往往会将相似的记录归为一组,以消除它们的差异,从而防止任何单一记录被唯一识别。这种设计的一个直接后果是,属于同一子群的记录更有可能被归为一组。考虑一种情况,即同一亚人群的所有记录都被归入一个组,其结果变量值全部由组平均值代替。很明显,这使得任何通过隔离进行的差异性测试更有可能宣布差异的假阳性结果,其原因是亚人群内的方差被人为地减少到零。
当差异通过变差差异进行操作时,以上推论不再适用,因为变差差异的识别只取决于点估计值而不是标准误差。尽管如此。它将数据移除对点估计的潜在偏差置于首要地位。我们在概念构建部分展示了一个例子(图3),其中数据移除严重改变了观察到的结果分布。下面的定理扩展了这个例子 突出了结果分布偏斜时问题的严重性,如在实践中常见的重尾分布。在重尾分布中,最大的数值与最低的概率密度有关,这意味着删除具有最稀疏邻域的记录往往会大大降低平均估计值。该定理将指数分布作为一个保守的例子,因为它的偏度可以作为重尾分布的偏度的下限。
定理2:当Yi遵循指数分布Yi~Exp(λ)时,根据Yi的密度删除Yi的n条记录中的m条,使Yi的样本平均值的预期值为:
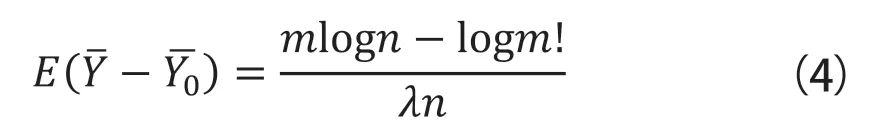
其中,分别是数据移除前后的样本标准差。
该定理证实了我们的概念讨论,证明了少数被移除的记录如何对点估计值(如样本平均值)产生相当大的影响。例如,从一个有100条记录的数据集中删除10条记录,样本平均数的预期变化量为0.45/λ。由于指数分布的平均值Exp(λ)是1/λ,这个预期变化代表了实际值的45%,显然大到足以翻转差异测量的结果。
最后,我们把注意力转向匿名化的噪音插入机制。有趣的是,与数据移除不同,噪声插入技术的设计者经常提供关于插入的噪声如何影响回归分析的输出的统计保证。例如,当噪声插入技术直接修改查询答案时(例如前面提到的拉普拉斯机制),我们可以把回归系数理解为对数据提出的复杂查询。然后,添加到查询答案中的随机噪声直接揭示了我们对回归系数估计的统计属性。这使得我们在这里的分析变得相当容易。具体来说,许多现有的噪音插入技术,包括拉普拉斯机制,产生的估计值保证是无偏的。1Cynthia Dwork, Frank McSherry, Kobbi Nissim and Adam Smith, Calibrating Noise to Sensitivity in Private Data Analysis, Journal of Privacy and Confidentiality, vol. 7, no. 3, 2016, pp. 17-51.虽然其他技术可能会引入小程度的统计偏差,以换取大幅减少的标准误差,但这种偏差往往很小,并且随着数据集规模的增长而渐进地接近于零。2Li Ninghui, Wahbeh Qardaji and Dong Su, On Sampling, Anonymization, and Differential Privacy or, K-Anonymization Meets Differential Privacy, Proceedings of the 7th ACM Symposium on Information, Computer and Communications Security,2012, pp. 32-33.因此,当差异性通过变差差异来操作时,噪声插入显然既可以产生假阳性结果,亦可以产生假阴性结果。对于通过隔离操作的差异性,下面的定理为任何噪声插入算法的任何差异性测试的统计能力建立了一个上限,该算法是(ε,δ)-差分隐私。
定理3:对于任何(ε,δ)-差分隐私算法,当Zi∈{0,1},Zi遵循独立同分布(单变量或多变量)高斯分布,且Yi=β0+β1 Xi+β3 Zi+εi,任何差异性通过隔离测试的统计功效(statistical power)必须满足

其中,α是差异测试的显著性水平,n是数据样本中的记录数,σ是β1 Xi+εi的样本标准差。
不等式5中的约束为隐私保护和差异识别之间的权衡提供了重要的见解。例如,ε,δ越小(即越严格的隐私保证),统计功效就越低。因此,严格的隐私保护是以差异检测为代价的。例如,要求隐私预算为ε=0.001意味着差异检测的统计功效在匿名化后可能从100条记录的原始数据集的0.80最多下降到这证实了我们的概念构建,即当差异性通过隔离进行概念化时,噪声插入可以掩盖数据集中相当数量的差异性。
四、实证检验
(一)数据集
我们从美国人口最多的五个州之一获得了一个住院病人数据集。该数据集包含486924条患者记录,这些患者在一个日历季度内被该州的一家医疗机构入院并出院。数据涵盖了244家医疗机构,代表了该州所有接收住院病人的私有机构,但三类豁免机构除外:长期急性护理机构、精神病和康复机构,以及不符合规定的机构。从一个医院出院的病人数量从5到9104不等。每个病人关联的变量涵盖了人口统计、诊断、治疗和财务安排等信息。
我们使用这个数据集的一个重要原因是它与得克萨斯州卫生服务部(2019)根据表1的匿名化方法处理的住院病人数据集非常相似。由于得克萨斯州不允许在匿名化之前发布其数据集,我们的数据集成为研究应用得克萨斯州程序的影响的理想参照。虽然我们也研究了其他一些技术上更复杂的匿名化技术(如本节后面所阐述的),但我们认为对得克萨斯州程序的研究很重要,因为它代表了一个目前而言比较罕见的情况,即政府机构明确规定了对含有高度敏感私人信息的数据集进行匿名化的步骤。
(二)实证研究设计
1.差异化测度
自变量:我们使用了两个在健康差异背景下经常被研究的自变量:入院严重程度(SERV)和无反应指标(NONRES)。入院严重程度按5分制测量(从0到4,即从无临床不稳定到最大不稳定)。无反应者指标反映了病人在住院期间对治疗是否有反应,通过比较住院中期收集的临床变量和入院时收集的变量而确定。如果患者在住院中期根据临床变量预测的院内死亡概率高于入院时,则被视为无反应者。
我们选择这两个因变量的一个重要原因是它们具有鲜明的特点。在我们的数据集中,所有的医院都被要求收集入院严重程度(SERV)的信息,使其在数据集中的覆盖率接近100%。相比之下,无反应指标则是可以选择报告的。此外,入院时被认为具有中度或低度临床不稳定性的患者没有资格进行计算。因此,数据集中只有4.3%的记录包含病人是否为无反应者的二进制判断(是/否)。两个因变量之间的这种鲜明对比使我们能够研究两种不同的情况。1)结果变量适用于数据集中的所有个人(如收入差距),以及2)结果只适用于一小部分个人(如晋升行政职位的差距;罕见疾病的差异研究;或在苹果iOS的案例中,只有一小部分按键需要纠正)。
社会决定因素:为了检测差异,分别将性别、种族、民族和年龄作为重点社会决定因素进行研究。选择这四个变量有两个主要原因。首先,这些变量经常是差异研究中的焦点因素。其次,在隐私方面,它们也经常被视为“准识别符”1Sweeney Latanya, Simple Demographics Often Identify People Uniquely, Health, vol. 671, 2000, pp. 1-34.,因此为了匿名的目的,这些变量经常按照表1所示的程序那样被有选择地删除或掩盖。鉴于它们在数据匿名化和差异检测中的突出地位,对这些变量的关注使我们能够更好地解释前者对后者的影响。
控制变量:为了进一步模仿差异研究文献中通常进行的分析,我们还将三个个人层面的变量作为实证研究的控制变量。1)保险状况(INS;一个二元变量,表示个人是否有医疗保险);2)癌症史(CANCER;一个二元变量,表示个人是否有癌症诊断史);以及3)住院天数(LOS;一个整数变量,广泛用于代表个人医疗状况的复杂性)。选择这些控制变量是因为它们与病人的财务状况或医疗状况相关,在健康差异的文献中经常被用作控制变量。
差异检测:我们考虑了对应两种差异操作化的两种差异分析方法,即回归分析和几率比。对于通过隔离实现的差异(disparity through separation),我们使用公式1中的回归模型进行分析。具体来说,估计结果变量(如入院严重程度)相对于重点社会决定因素(如种族)的差异。公式中结果变量是Y,重点社会决定因素是Z,其他三个社会决定因素和三个控制变量组成X。我们为性别和种族创建了虚拟变量,当因变量是入院严重程度时,使用普通最小平方估计模型。由于其他因变量(即无应答者指标)是二进制的,我们使用最大似然估计的逻辑回归。对于通过变差实现的差异(disparity through variation),我们考虑了经常使用的几率比的测量方法,计算方法见公式(6):

其中X、Y和Z如公式1所定义,V0和V1是Z域的两个子集。直观地说,几率比反映了在保持X不变的情况下,将Z从V0转移到V1对Y=1的几率的影响。几率比的估计可以通过逻辑回归来完成,具体为eβ,其中β是Z的回归系数。为了使因变量Y成为二进制,在计算入院严重程度(SERV)的赔率时,我们将其五个值分为两组,以中位数划分:{0,1}为一级,{2,3,4}为另一级。
2.数据匿名化技术
为了研究不同的数据匿名化机制对差异检测的不同影响,我们总共实施了四种数据匿名化算法,其中两种是数据移除,另外两种是噪声插入。我们实施的第一个算法是得克萨斯州卫生服务部(2019年)用于匿名化全州住院病人出院数据集的规则(表1)。虽然所有的规则都适用于我们的数据集,但有两个小的调整是必要的。首先,我们将规则2中的得克萨斯州改为我们数据集中的州。第二,由于我们的数据集包含ICD-9而不是ICD-10编码,所以在应用规则3时,我们确定并使用了表示酒精/毒品使用或HIV18的ICD-9编码。我们在研究中发现,对差异检测有实质性影响的只有规则3和8,因为它们删除了我们的差异分析中包括的社会决定因素。由于规则8有一个可调整的参数(即10个病人的阈值),我们还测试了阈值为20时的规则变体。
接下来,我们考虑了K-匿名算法,这是欧盟咨询机构为消除个人识别风险而推荐的一种数据删除机制。我们使用了sdcMicro R包中的局部抑制算法。该算法旨在删除尽可能少的变量值,以实现k-匿名性。为了研究最小匿名化(即k=2)如何影响差异检测,我们在研究中测试了k=2和5的情况。
对于线性回归,我们使用最近开发的差分隐私充分统计扰动(SSP)算法的变体,1Wang Yuxiang, Revisiting Differentially Private Linear Regression: Optimal and Adaptive Prediction & Estimation in Unbounded Domain, arXiv preprint arXiv:1803.02596, 2018, pp. 1-30.该算法通过首先分别计算XT X和Xy的差分隐私版本,在生成估计系数为之前,保证在求解线性模型y=Xβ+ε时具有(ϵ,δ)差分隐私。与原始的SSP算法相比,我们所使用的算法变体进一步利用了数据相关的量化方法来实现接近最佳的数据效用,并被证明大大超过了其他现有的差分私有线性回归的解决方案。由于δ通常被设定为一个可忽略的值,我们设定2Wang Yuxiang, Revisiting Differentially Private Linear Regression: Optimal and Adaptive Prediction & Estimation in Unbounded Domain, arXiv preprint arXiv:1803.02596, 2018, pp. 1-30.其中n是数据集大小,ϵ并在0.1和1之间变化。
对于逻辑回归(以及相关的几率估计),我们实施了正则化经验风险估计的差分隐私算法,3Chaudhuri Kamalika, Claire Monteleoni and Anand D. Sarwate, Differentially Private Empirical Risk Minimization,Journal of Machine Learning Research, vol. 12, no. 3, 2011, pp. 1069-1109.它比传统的输出扰动算法(如上述的拉普拉斯机制)产生更准确的系数估计,因为它通过扰动优化过程的目标函数而不是系数估计的最终输出来实现差分隐私。该算法被设计为实现(ϵ,0)-差分隐私,其特点是只有两个参数ϵ和λ,这是控制l2-正则化项的正则化参数。我们在实现中设定其中n是输入大小,ϵ在0.1和1之间变化。
(二)实证估计结果
数据移除对隔离差异的影响:分析结果表明(篇幅限制不展示分析结果的表格,相关结果请参见论文原文),实践中使用的数据移除匿名化方法,如得克萨斯程序,可以大大干扰隔离差异。在k-匿名的情况下,即使是最弱的匿名形式(即k=2)也会对亚洲人的入院严重程度产生假阳性差异。这种干扰可能是朝着任何一个方向。例如,对于西班牙血统的人,得克萨斯程序识别出的入院严重程度明显较低,k-匿名(k = 5)识别出的严重程度明显较高。然而,未经过匿名操作的原始数据不能支持以上两个结论。从表中还可以看出,与定理1一致,k-匿名算法倾向于产生更多的假阳性而非假阴性。
数据移除对变差差异的影响:得克萨斯程序和K-匿名方法都对变差差异结果产生了很大的影响,甚至在一些情况下还扭转了其方向。这与我们之前的概念讨论和定理2是一致的。与数据移除对隔离差异的影响相比,当差异性通过变异来操作时,K-匿名性除了产生假阳性之外,还掩盖了差异性的严重性。例如,实现2-匿名性需要将亚洲人成为无反应者的几率比从2.79降低到1.52,如果使用 “多半可能”(more likely than not)的标准,则会产生假阴性。
噪声插入对隔离差异的影响:即当差异性通过隔离来操作时,差分隐私算法很可能会产生假阴性结果。值得注意的是,即使当ϵ=1,即一个在实践中被认为是隐私保护程度很弱的水平,1Cynthia Dwork, Frank McSherry, Kobbi Nissim and Adam Smith, Calibrating Noise to Sensitivity in Private Data Analysis, Journal of Privacy and Confidentiality, vol. 7, no. 3, 2016, pp. 17-51.差分隐私算法仍然以99%的假阴性率掩盖了无反应指标的(唯一)统计意义上的差异性。
噪声插入对变差差异的影响:与数据删除机制一样,噪声插入算法以不可预测的方式改变了差异的估计大小,对一些人来说放大了几率比,对另一些人来说削弱了几率比,甚至在一些情况下逆转了变化的方向。
五、讨 论
(一)政策与管理启示
保护消费者隐私已经成为数字经济背景下企业和政策制定者的一项首要任务。同样,对不同群体间基于数据的推理预测的差异性的认识与纠正也越来越被视为就业、住房、医疗保健等方面的社会必要条件。这两个问题的首要地位在未来只会因为快速增长的消费者数据收集和多样化的技术问题而得到加强,而隐私和群体差异的问题也经常由此产生,这使得研究人员、从业人员和政策制定者更加需要注意这两者之间潜在的复杂的相互作用,这也是本文的重点。在此背景下,我们的结果强调了研究隐私保护对不同个体的不同影响的重要性,并阐明了在隐私保护的数据中识别差异的复杂性。在下文中,我们将根据我们的发现提供可操作的建议,以确保匿名化的设计和差异化的操作之间的适当协调。
首先,当数据集已经被匿名化时,在审查差异影响的统计证据之前,对所应用的匿名化机制做出说明是非常重要的。例如,如果应用了噪音插入,通过隔离来操作差异性往往会产生保守的结果,产生假阳性的可能性很小。因此,这样的结果至少与原始数据集上的结果一样有效。此时如果在匿名数据中检测出群体差异,则可以建立歧视存在的初步证据。相反,如果应用了像K-匿名这样的数据清除机制,那么更有可能产生假阳性而不是假阴性的结果。因此,这些可能更好地作为探索性步骤,以确定是否需要对特定类型的差异性影响进行进一步研究。鉴于企业在收集数据时越来越流行使用匿名化技术或基于保留隐私的数据做出分析决定,了解匿名化和差异性检测之间的这种微妙互动越来越重要。
其次,匿名化的设计应该同时考虑保护隐私和匿名数据在差异性检测中的影响。文献已经反复指出这两个目标之间的必要权衡。更重要的是,现有的噪音插入技术被证明可以在某些假设下在这个权衡上实现帕累托最优。对于数据移除,虽然实现最优性被证明是困难的,但研究人员已经开发了在最优权衡的一个恒定系数内达到最优性的近似算法。1Aggarwal Gagan, Tomas Feder, Krishnaram Kenthapadi, Rajeev Motwani, Rina Panigrahy, Dilys Thomas and An Zhu,Approximation Algorithms for K-anonymity, Journal of Privacy Technology (JOPT), vol. 11, 2005, pp. 1-18.这些结果不仅提供了适合差异检测目的的匿名化机制,而且有助于说明当数据集必须被匿名化以满足某些隐私保证时,在差异检测方面会导致什么结果。对匿名化下隐私保护和差异检测的权衡的了解,反过来将使监管者和政策制定者在强制或激励隐私保护(如通过GDPR等隐私立法)或为差异检测收集社会决定性信息之前,能够正确评估隐私保护(和披露)对不同亚人群的不同影响。
(二)局限性和未来研究
我们的工作受限于它只对可观察到的差异的检测,而不是对任何潜在的因果歧视的确认。值得注意的是,即使是数据集中的巨大和持续的差异也不能证明歧视,因为后者需要对数据产生的机制有大量的预先了解。例如,在支持歧视的因果推论之前,我们必须从遗漏的变量和常见的偏见(如样本选择偏见)中找出内生性威胁。2Pager Devah and Hana Shepherd, The Sociology of Discrimination: Racial Discrimination in Employment, Housing,Credit, and Consumer Markets, Annual Review of Sociology, vol. 34, 2008, pp. 181-209.为此,我们的工作只是理解数据匿名化对识别歧视的影响的第一步。未来的研究可以研究数据匿名化如何影响因果推理的后续步骤。
我们工作的另一个局限性与匿名化数据的其他潜在影响有关。虽然当可识别的差异被掩盖时,显然会对贫困亚群产生不同的影响,但这种不同的影响也可能来自匿名数据的其他用途,例如,当数据被用于分配教育和医疗保健等资源时。3Ekstrand Michael D., Rezvan Joshaghani and Hoda Mehrpouyan, Privacy for All: Ensuring Fair and Equitable Privacy Protections, Conference on Fairness, Accountability and Transparency, 2018, pp. 35-47.4Pujol David, Ryan McKenna, Satya Kuppam, Michael Hay, Ashwin Machanavajjhala and Gerome Miklau, Fair Decision Making Using Privacy-Protected Data, Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, 2020, pp. 189-199.有趣的是,如果我们将分析单位从子群体转换为个人,那么匿名化已被证明可以防止某些歧视,未来的研究可以进一步研究数据匿名化的这些反作用,以便企业在选择应用数据匿名化机制时可以适当地平衡它们。
最后,我们对匿名化机制和差异化操作的分类,是为了强调不同类型之间细微差异和相互作用,而不是作为一种严格的二元分类。因此,尽管本文提出的分类具有普遍性,但也存在例外情况。例如,在评估就业歧视时,隔离差异是一种主要的计算群体间差异的方法,但是美国平等就业机会委员会也提出了一种通过变差差异衡量就业歧视的著名的经验法则。同样,在匿名化技术方面,数据移除和噪声插入也不总是依从二元分类的,目前有一些匿名化技术的尝试就是既能去除数据又能插入噪音。5Li Ninghui, Wahbeh Qardaji and Dong Su, On Sampling, Anonymization, and Differential Privacy or, K-Anonymization Meets Differential Privacy, Proceedings of the 7th ACM Symposium on Information, Computer and Communications Security,2012, pp. 32-33.然而,这些例外情况的存在并不影响我们的关于数据匿名化对差异识别的影响的结论。
