Bounded multi-soliton solutions and their asymptotic analysis for the reversal-time nonlocal nonlinear Schrödinger equation

Wei-Jing Tang, Zhang-nan Hu and Liming Ling

Department of Mathematics, South China University of Technology, Guangzhou, 510641, China

Abstract In this paper, we construct the Darboux transformation (DT) for the reverse-time integrable nonlocal nonlinear Schrödinger equation by loop group method.Then we utilize the DT to derive soliton solutions with zero seed.We investigate the dynamical properties for those solutions and present a sufficient condition for the non-singularity of multi-soliton solutions.Furthermore,the asymptotic analysis of bounded multi-solutions has also been established by the determinant formula.

Keywords: nonlocal nonlinear Schrödinger equation, multi-soliton solution, singularity,asymptotic analysis

1.Introduction

Integrable nonlocal nonlinear Schrödinger equations(nNLSE)play a vital role in mathematical physics[1–8]and have been studied extensively [9–15].This type of equation is symmetric because it is invariant under the joint transformation x → −x, t → −t and complex conjugation.For a AKNS spectral problem, the reductionr(x,t) =σq(x,t)*σ= ±1 was thought to be the only interesting one until 2013.However, Ablowitz and Musslimani [9] discovered that there existed another interesting reductionr(x,t) =σq*(-x,t)which results in a new form of integrable nNLSE:

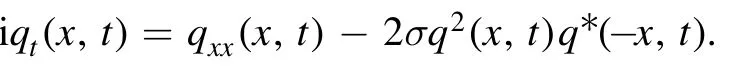
It was not long before they found two more reductions of the AKNS scattering problem:r(x,t) =σq(-x,-t)andr(x,t)=σq(x,-t), which gave rise to the so-called reverse-space–time NLS and reverse-time NLS equations,respectively reported by[16]

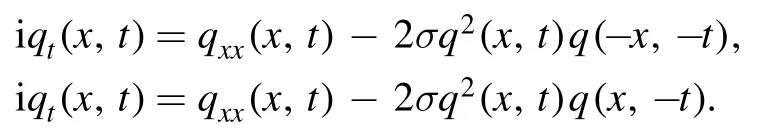
In this paper, we focus on a nonlocal reverse-time NLS equation [16, 17]

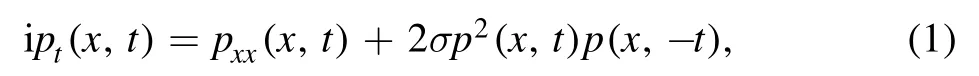
which was generalized by Ma [18] to a multi-component one.Yang [17] has derived general multi-solitons in three types of nNLSE, including the reverse-time, reverse-space and reversespace–time nNLSE, and also presented a unified Riemann–Hilbert framework for them.Ma utilized inverse scattering transformation to construct N-soliton solutions to multi-component nNLS equations under the framework of Riemann–Hilbert problem[18].There are also many other scholars who have made their own contributions to the study of reverse-time nNLSE.Lou[19]have established some new types of methods to solve nonlinear systems,as the full reversal invariant method and so on.Very recently, Ye and Zhang [20] constructed the general soliton solutions with zero and non-zero background to a reverse-time nNLSE via a matrix version of binary Darboux transformation(DT).They derived the formula of multi-soliton and high order solitons in a determinant form.It is seen that the single-soliton could exponentially blow up or decay.The asymptotic analysis has been established on two-soliton solutions for the nonlocal complex coupled dispersionless equation [21].

In fact, the soliton solutions of the integrable equation can be constructed by many methods, such as the inverse scattering method [22–26], the Hirota bilinear method[27–29], the DT [30–32] and so on.As we know that, for a physical system it is more interesting to find the bounded nonsingular multi-soliton solutions.For a nonlocal integrable model, there will be problems such as singularity and boundedness in the process of searching for soliton solutions,and there are few studies in this area[33,34].In this work,we would like to explore a sufficient condition for the bounded multi-soliton solution for the nonlocal time-reversal NLS equation.What is more, the asymptotic analysis of bounded multi-soliton solutions to the reverse-time nNLSE can be established.

In this paper we use the DT method to construct the multi-soliton solutions for nNLSE (1) with the aid of loop group method [35].By the construction of loop group method, the soliton solutions admit the compact determinant representation, which is beneficial to analyze the singularity of soliton solutions.Then we present a sufficient condition for a symmetric bounded multi-soliton solution.Furthermore,the asymptotic analysis for the multi-soliton solution is performed by the determinant technique,in which the modulus of multisoliton solutions can be approximately decomposed into the sum of single-soliton solutions.The multi-soliton solutions exhibit the similar structure as the classical NLS equation,but they can not be decomposed directly since the phase term has the indefinite limitation.But we find the modulus of the multisoliton solutions can be decomposed ast→±∞.Our proposed method provides a way to implement the singularity and asymptotic analysis for the time-reversal nonlocal integrable system, and it can be extended to other nonlocal NLS equation and vector nonlocal NLS equation [36–38].

The rest of the paper is organized as follows.In section 2,we will develop the N-fold DT for equation (1) by the loop group method.In section 3, the soliton solutions for equation (1) will be constructed through DT with zero seed.Besides, we will analyze the singularity and asymptoticity of the solutions that we have obtained.In the final section, we will give a few discussions and conclusions.

2.DT for the time-reversal nonlocal nonlinear Schödinger equation

As the nNLSE (1) can be regarded as a special reduction of the AKNS system, we firstly consider the AKNS system without reduction in order to obtain the DT for nNLSE (1)later.The AKNS system that we are going to explore is as follows:

where

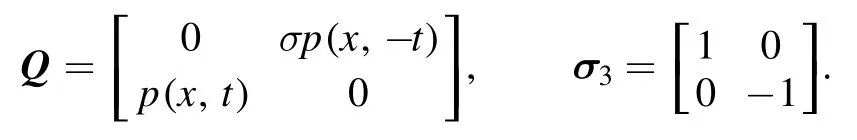
Meanwhile, note that the reverse-time character implies the following symmetric relationship betweenUandVmatrices[18, 39]:

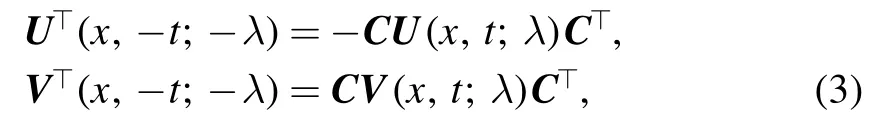
where

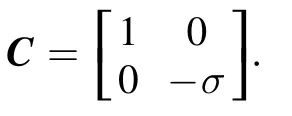
Based on the symmetric relation (3) and the existence and uniqueness of ordinary differential equation, we have

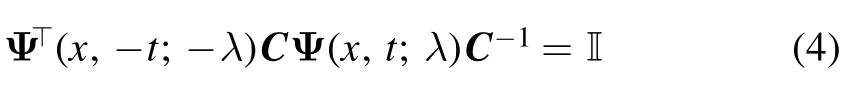
with the condition Ψ (0 , 0;λ) = I.Moreover, if the column vector solutionψ1(x,t;λ1) is the solution of Lax pair (2) atλ=λ1,then the rowvector solution(x,-t;λ1)Csatisfies the following adjoint Lax pair:

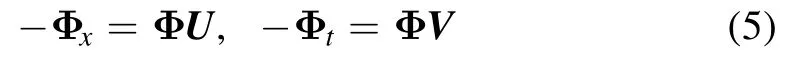
atλ= -λ1.

Combining the loop group method [35] and the above symmetric relationship (3), it follows that the DT for system(2) can be represented as

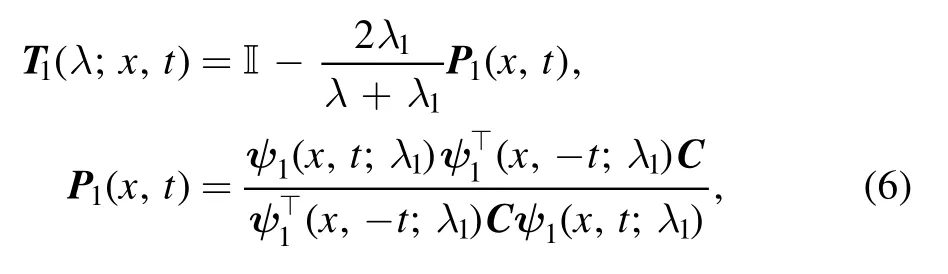
where theψ1(x,t;λ1)in DT is a special solution to system(2)atλ=λ1.Asψ1(x,t;λ1) can be written asthe corresponding Bäcklund transformation between old potential function and new one is given by

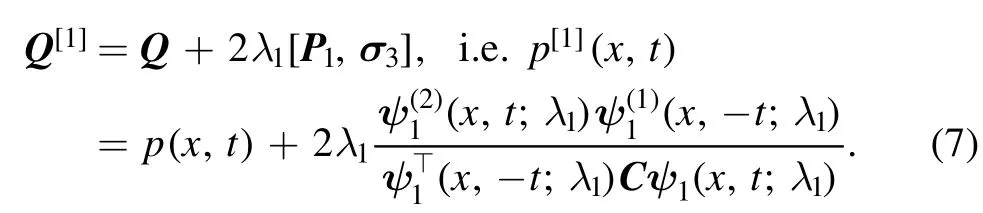
In what follows, we verify the validity of above DT (6) and the corresponding Bäcklund transformation(7).Then,we can establish the following theorem:

Theorem 1.The DT(6)converts Lax pair(2)into a new one

whereΨ[1](x,t;λ) =T1(x,t;λ) Ψ(x,t;λ),andQ[1]is given by equation (7).

Proof 1.The proof of this theorem is equivalent to verify the following two equations:

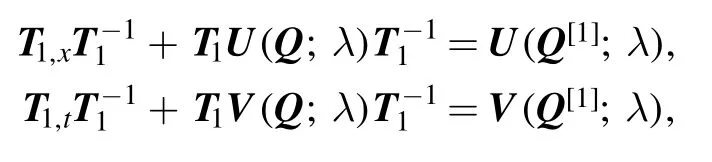
and the symmetric relationship (3).Defining

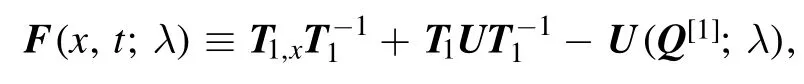
through direct calculation, we have

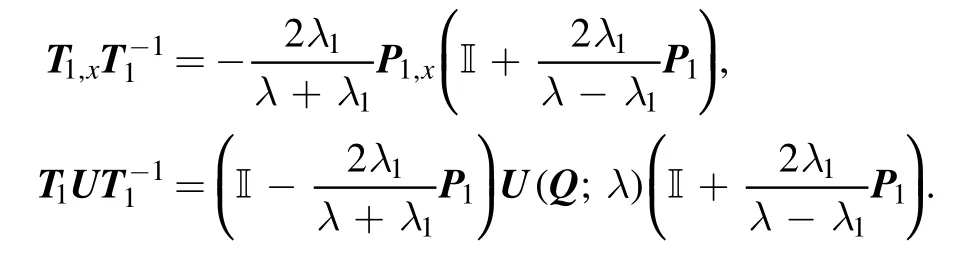
Based on above equations, we can obtain the residue for functionF(x,t;λ) as

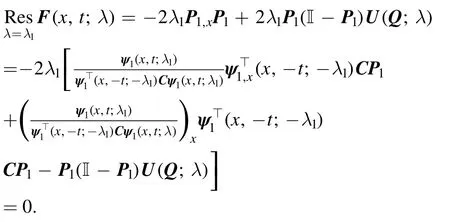
Defining

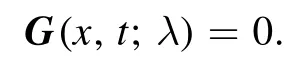
Furthermore, with direct calculation, we can verify that

Now we proceed to prove the symmetric properties ofU[1]andV[1].SinceΨ†(x, -t; -λ)CΨ(x,t;λ)C= I, then

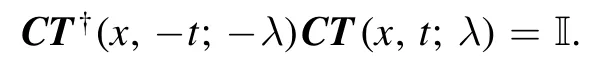
FromU†(x, -t; -λ) = -CU(x,t;λ)C⊤andU[1](x,t;λ)=it follows that

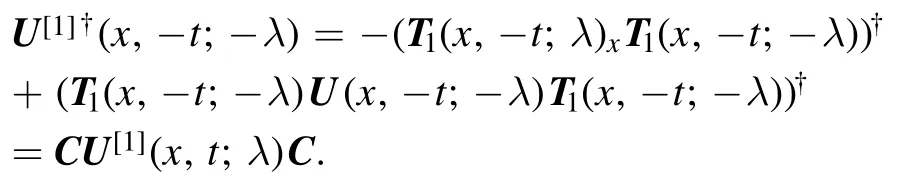
and throughV†(x, -t; -λ) =CV(x,t;λ)C⊤, we have

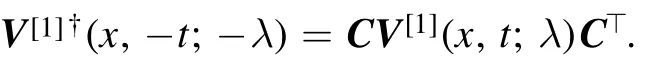
This completes the proof.

The above elementary DT can be iterated one by one to yield the N-fold DT.With the knowledge of linear algebra and complex variables functions, the iterated N-fold DT can be represented in a compact form.Then the multi-soliton solution can be constructed through the formula of corresponding Bäcklund transformation.In general,we can establish the following N-fold DT for nNLSE (1) as

Theorem 2.If we have N different solutions to system(2):ψ1(x,t;λ1) ,ψ2(x,t;λ2), …,ψN(x,t;λN) withλ=λi,i= 1, 2, …,N,λi≠λj(i≠j),λi≠0, then the N-fold DT can be represented as

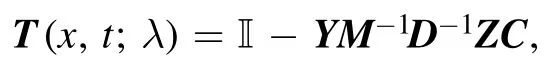
where

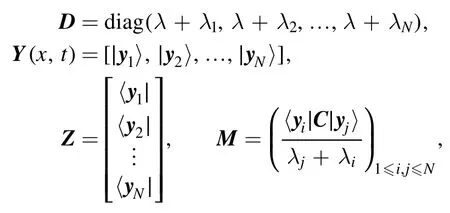
〈yj∣≡ψj(x,-t)⊤,∣yi〉 ≡ψi(x,t).And the corresponding Bäcklund transformation between old and new potential functions is given by

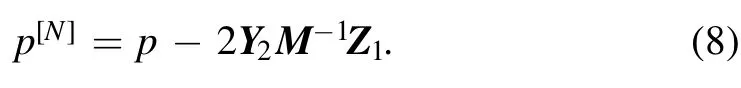
Proof 2.The recursive DTs between matrix functions are given as

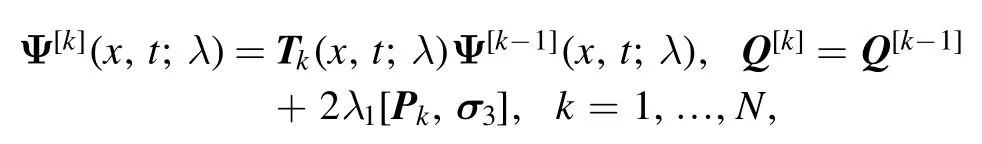
where

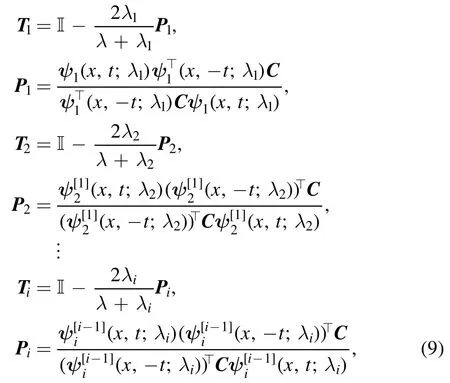
and

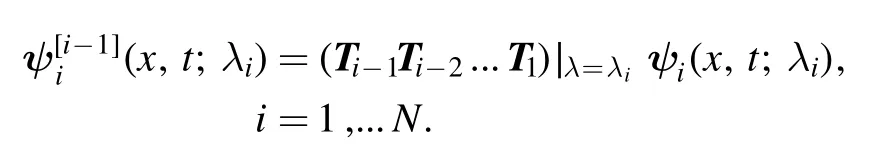
Defining

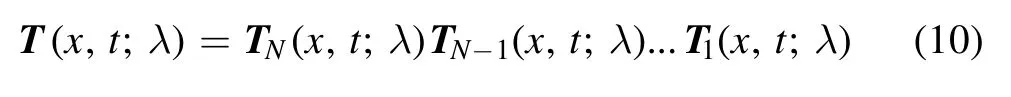
which represents the N-fold DT, and analyzing the form of equation (10), it immediately comes out thatT(x,t;λ) is a meromorphic function and ∞is not the essential singularity,so it is a rational function with respect to λ.Then the N-fold DTT(x,t;λ) can be expressed in the form of

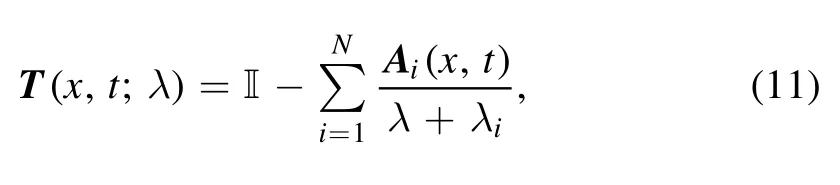
whereAi(x,t) is a matrix.By calculating residues on both sides of equation (11), an expression ofAi(x,t) is obtained:

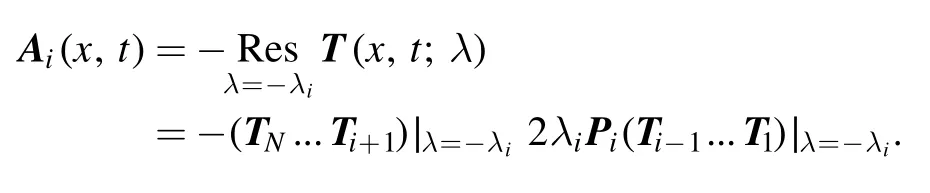
From equation (9) we know that rank(Pi) =1, thus rank(Ai(x,t)) =1.According to the knowledge of linear algebra,Ai(x,t) could be rewritten as

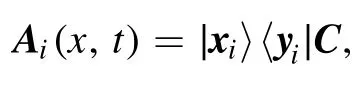
where ∣xi〉is a column vector, and〈yi∣is a row vector.For simplicity, we denote that

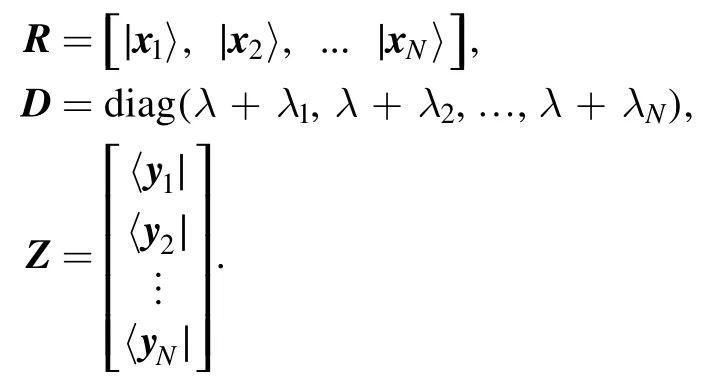
ThenT(x,t;λ) can be rewritten in matrix form as

Besides, after observation and inspection, we obtain that ker (T(x,t;λi)) =ψi(x,t;λi), i.e.

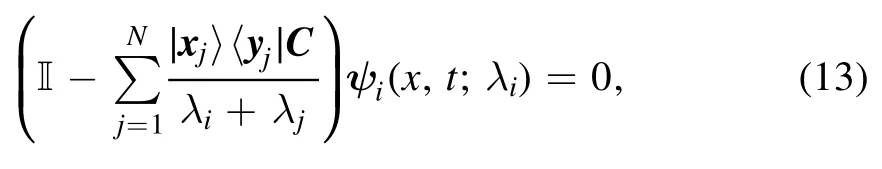
which implies that

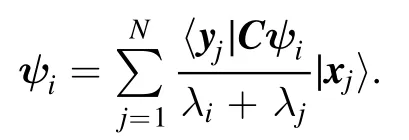
Thus

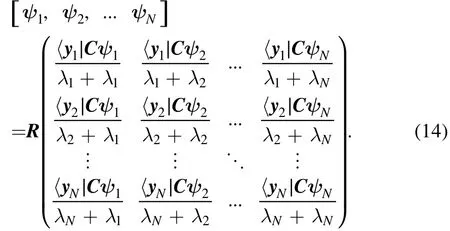
Furthermore, it is readily verified that

i.e.

Calculating residues on both sides of equation (15), then we obtain that

Because〈xi∣ ≠0,comparing equations(13)and(16),we find that

Denote

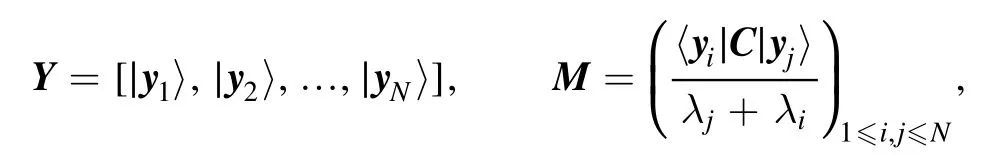
then equation (14) can be rewritten as

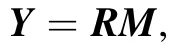
thus

Finally, by substituting equations (18) into (12), we obtain that

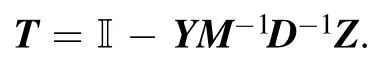
The Bäcklund transformation(8)can be obtained through the formula

by expanding with respect to λ at the neighborhood of ∞.

So far we have constructed the N-fold DT,and in the next section it will be utilized to derive the N-soliton solution,based on which the singularity and asymptoticity analysis on these solutions will have been done.

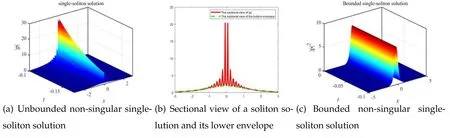
Figure 1.(a)By choosing the parametersc = 1,σ = -1,we obtain an unbounded non-singular single-soliton solution.(b)The corresponding sectional view of the single-soliton solution in (a) and its lower envelope.(c) By setting a1 =0, b1 =1, c = 1 +i,σ = -1, we obtain a bounded non-singular single-soliton solution.

3.Bounded multi-solitons solutions and their asymptotic analysis

In this section, some exact solutions with zero seed solution will be derived.It is worth noting that the parameter σ in nNLSE represents different optical meanings, that is, σ takes±1 to correspond to focusing case and defocusing case respectively.As mentioned before, Ye and Zhang [20] have studied a reverse-time nNLSE withσ= 1, so we mainly discuss the situation whenσ= -1 here,because this situation has never been studied before.When discussing the asymptoticity of the solution, we quote two lemmas proposed by Zhang et al[40]to illustrate the properties of the modulus of the soliton solution.What is more, we utilize a kind of method proposed by Ling et al[15]to calculate the limit form of M-matrix.Also,another method proposed by Faddeev and Takhtajan [41] has been used to determine the exponential decay term of the remainder.

3.1.The dynamics for the single-soliton solution

Takingλ1=a1+ib1,a1,b1∈R and the seed solutionp(x,t) =0, then the vector solution of Lax pair (2) can be solved with the form:

whereη1(x,t) = iλ1(x+λ1t), and c1is a complex constant.Then, by the formula (7), we derive the following singlesoliton solution:

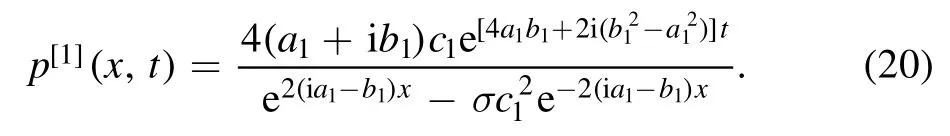
Now we analyze the dynamics for the single-soliton.

3.1.2.Boundedness.Whena1=0,σ= -1, we can obtain the bounded single-soliton solution with R (c1)≠0:

After calculation,we can deduce that the extreme point of the soliton solution is

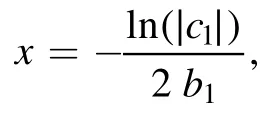
and its amplitude is

Similarly, we can consider the boundedness of solution for the caseσ= 1.It is seen that the boundedness of solutions is valid for the stationary one.

3.1.3.Oscillation effect.It is seen that the oscillation effect will appear in the solution as a1large enough, which had never been pointed out in the previous studies.After calculation, we obtain the bottom envelope of the oscillation (see the figure 1(b)), the expression of which is as follows

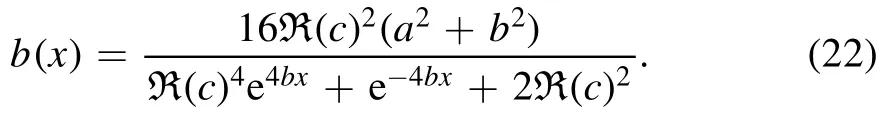
In principle,the expression of an envelope at the top can also be calculated, but the top envelope here is singular and has lost its practical significance, so it is not shown.In order to better represent the oscillation effect of soliton solution, we define its width.

Definition 1 The width of the soliton solution oscillation.The distance between the two abscissa corresponding to 1/2 of the maximum of the lower envelope is defined as the width of the soliton solution oscillation.

By equation (22) we obtain the expression of the width

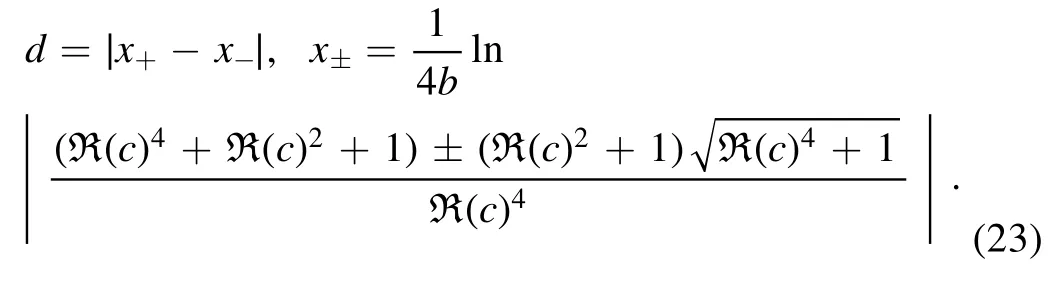
And it is readily proved that the period of oscillation is

so combining equation (22) with equation (24), we can deduce that the number of times that soliton solution oscillates is

where[] represents the ceil function.The single-soliton solution with oscillation effect and the sectional view of soliton solution and lower envelope are shown in figure 1.

Different from the single-soliton of classic NLSE, the amplitude of single-soliton solution of which is determined by the fixed spectral parameterλ1.From equation (21) we know that for the nNLSE(1)studied in this paper,the amplitude of the soliton solution is jointly determined by the spectral parameterλ1and the solution parameter c1.What is more, its amplitude can tend to ∞.Two examples of single-soliton solution are shown in figure 1.

Example 1.Choosing the parameters appropriately we have drawn graphs of unbounded single-soliton solutions and bounded single-soliton solutions.And from figure 1(a), we can see the single-soliton emerging the effect of periodic oscillation.Also,we provide the sectional view of the singlesoliton solution and the lower envelope.

In fact,it is not easy-to find the singularity conditions of the soliton solution, as the conditions are already very complicated only in the case of a single-soliton.In physics,we always pay much attention on non-singular and bounded soliton solutions.We have discussed these two features in the case of single-soliton.Fortunately, we have not only found the non-singular conditions and bounded conditions of singlesoliton solutions, we have also found those for the multisoliton solution.

3.2.The non-singular symmetric multi-soliton solution

For the convenience of discussion, we will take the solution parameter ciof each matrix functionψi(x,t) asbelow,then the matrix function of multi-soliton can be expressed as follows:

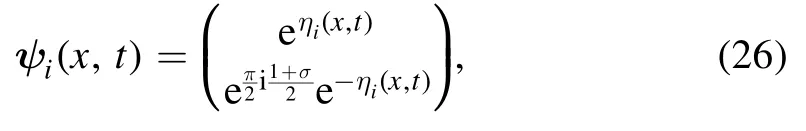
where

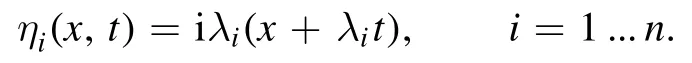
By the formula (8), we can construct the multi-soliton solution with the setting ofψi(x,t) (26):

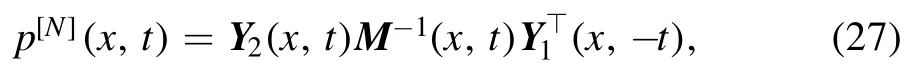
where

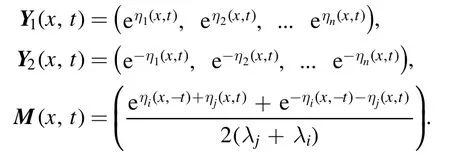
With the aim of better illustrating the properties of the soliton solutions, we first invoke two lemmas about the relations among the solution,the reverse-time solution and the M-matrix.

Lemma 1.[40]

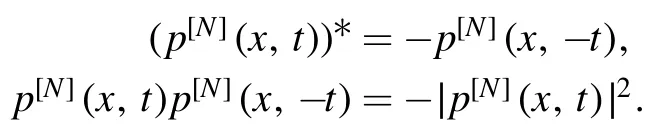
Proof 3.From equation (27), we can deduce that

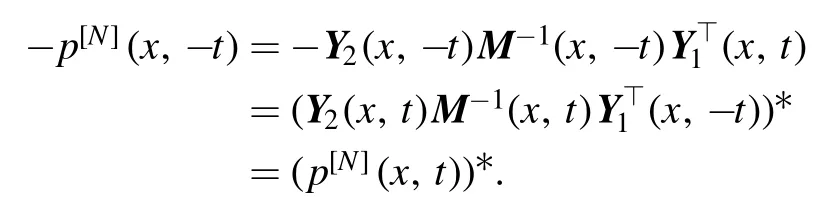
Then, naturally we have that

Following the method in [40], the following lemma can be established:

Lemma 2.[40]

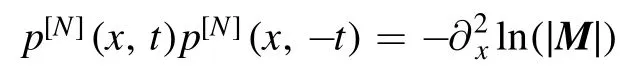
Proof 4.From theorem 2 we can perform the N-fold Darboux matrix as follows:

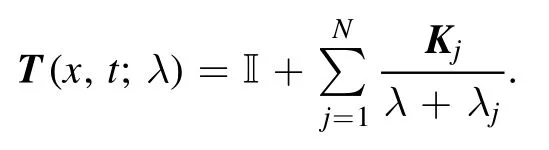
That Darboux matrix converts the system (2) into the invariant form

with

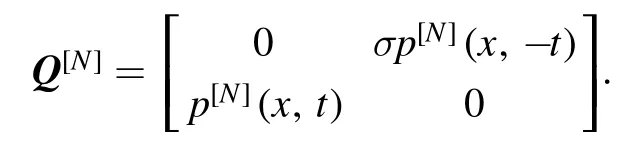
ByTx+TUbg(λ) =U[N]Tand matching the term O(λ-1),one yields

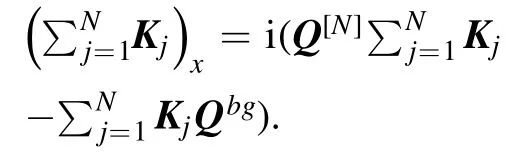
ByTt+TVbg(λ) =V[N]Tand matching the termO (1), one yields

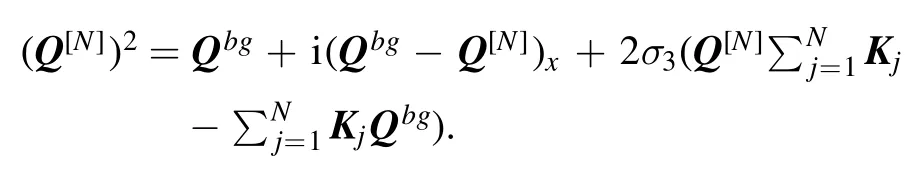
Combining the above two equations, one deduces

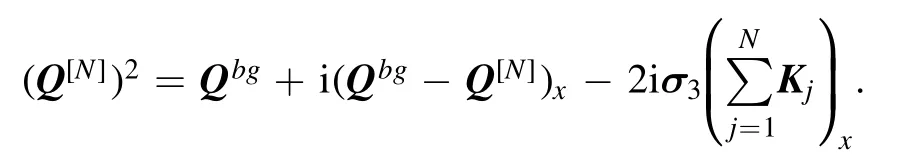
Then we derive

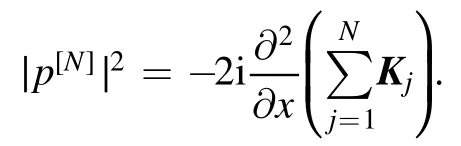
Note that

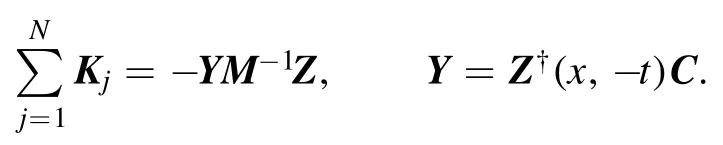
Then one obtains

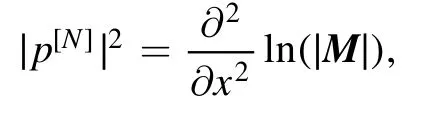
i.e.

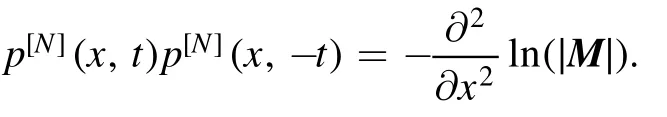
Then we provide a sufficient condition for a non-singular 2n-soliton solution.

Proposition 1.For a 2n-soliton solution, if the parameters satisfy

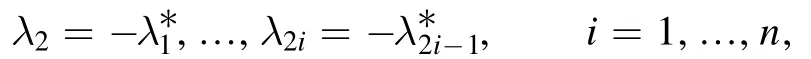
then the solutions constructed by theorem 2 are non-singular.

Note that throughout the paper we use*to denote complex conjugation.

Proof 5.Firstly, we verify thatMis non-degenerate.By theorem 2,Mcan be written asM= (mij)1≤i,j≤2n, where

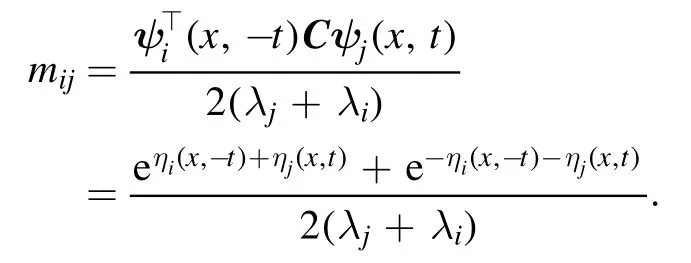
So the matrixMcan also be expressed in matrix form as

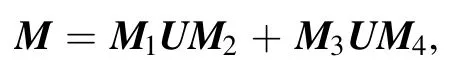
where

among which obviouslyUis a Cauchy matrix.Moreover,we readily come up with the following parameter relations:

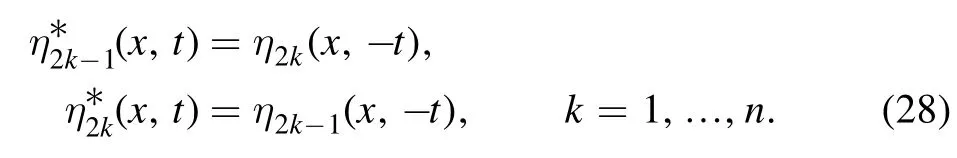
Besides, by equation (28) we can deduce that

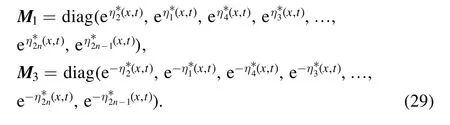
In order to make the proof clearer, we define a block matrix

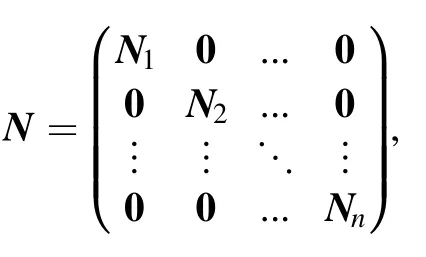
where

Furthermore, equation (29) implies that

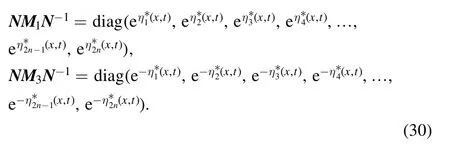
For simplicity, we denote that

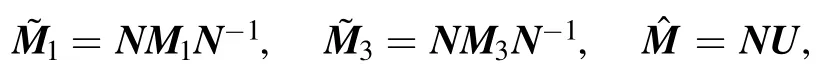
and it is readily verified thati.e.Mis a Hermitian matrix.We ulteriorly derive that

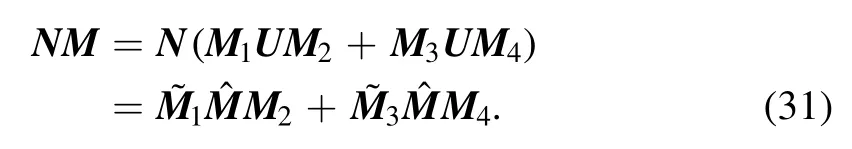
By setting thatHequals to equation(31),Hcan be written asH= (hij)1≤i,j≤2n, where

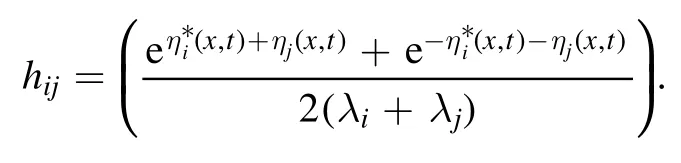
And because for anyξ i,ξj,

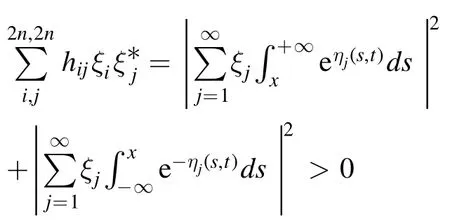
thusHis a positive definite matrix,which implies thatMis a non-degenerate matrix.

By theorem 2, a solution can be constructed in the form of

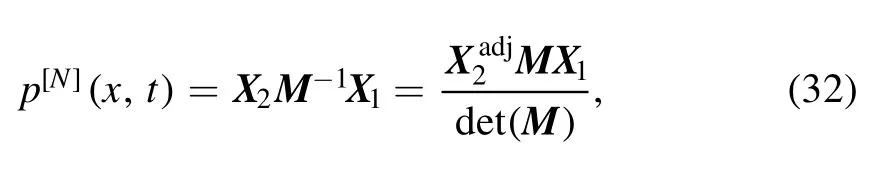
whereX1,X2are matrices obtained by the transformation of system matrix function.BecauseMis non-degenerate, i.e.det (M) ≠0, under the circumstancesp[N](x,t)must be a non-singular soliton solution.

Remark 1.In the above proposition, we give a sufficient condition for the2n-soliton solution with pair parameters.Actually, for the caseλi∈ iR, we can also obtain the similar result in a similar way.In this case, what we obtain are also the bounded non-singular soliton solutions.

3.3.Asymptotic analysis for the multi-soliton solution

In what follows, we will illustrate the asymptoticity of multisoliton solution underσ= -1.For the caseσ= 1, it can be analyzed similarly.In section 3.3, we set ci= 1 for convenience.We take thatλ1=a1+ ib1,λ2= -a1+ib1,because other forms of parameter selection result in that the derivation result in any direction equals to 0 in the limiting case.The corresponding matrix functions are as follows:

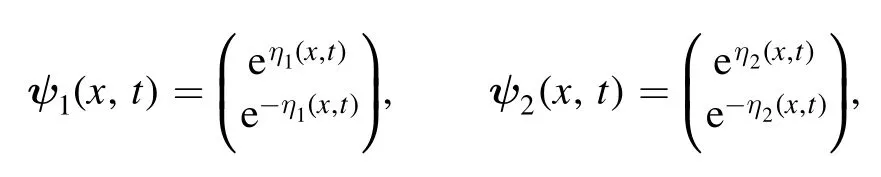
whereηi(x,t) = iλi(x+λit),i = 1,2.And then,throughout the theorem 2 we can derive the 2nd orderM2matrix:

For simplicity of expression, we denote that

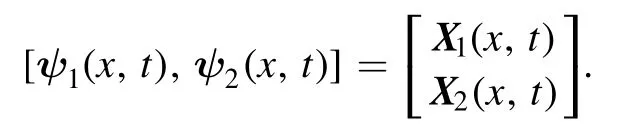
Then the solution could be written as:

Due to the symmetry of the solution with respect to the time variable t, here we only prove the case thatt→+∞.If we fix the direction asx+ 2a1t=θ1, thus

where

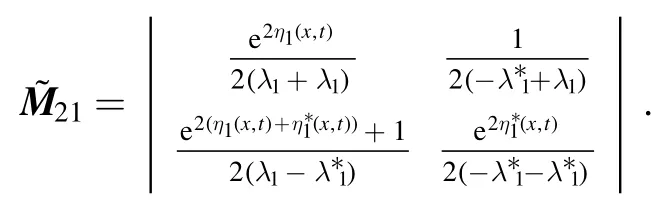
Similarly, we can obtain that if the direction is fixed asx- 2a1t=θ2,

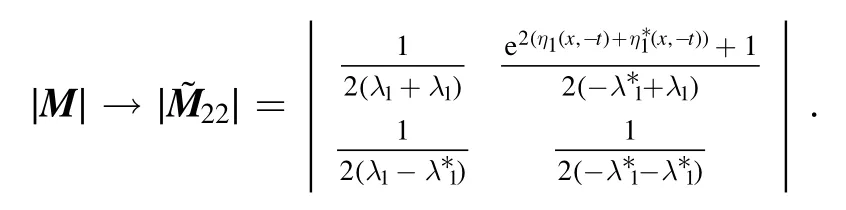
If we fix the direction to any other value, then we have

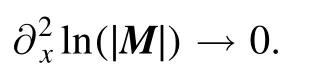
Therefore, from lemmas 2 and 3, we can derive that

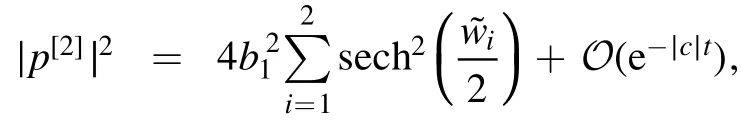
where

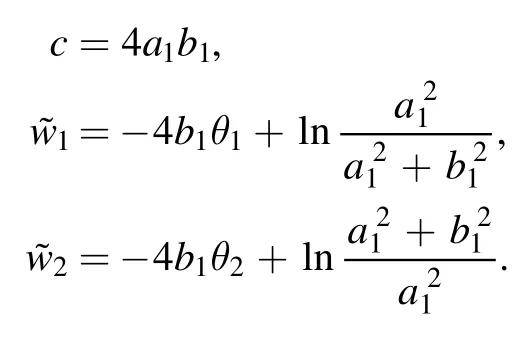
So far, the asymptotic form of two-soliton solution has been obtained.

Example 2.Choosing the parameters asa1= 1,b1=1,σ= -1, we construct the asymptotic form of the two-soliton solution.Due to the symmetry of the solution with respect to the time variable t, here we only show the sectional view whent→+∞.The results are shown in figure 2.

Note that the asymptotic analysis merely works for the multisoliton with different velocity.Next, on the premise of the sufficient condition for non-singular2n-soliton solution mentioned above, we give the asymptotic analysis of2n-soliton solutions.

Theorem 3.For a2n-soliton solutionp[2n], if the selected parameters satisfy the following conditions

then

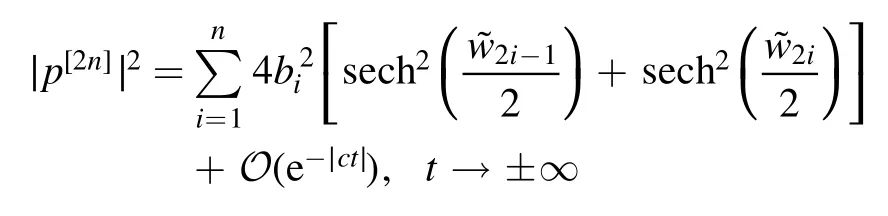
wherebi= I(λi), andare given by equations (37), (39), (41) respectively.In other words, whent→∞, the square of the modulus of a 2n-soliton solution can be written as the sum of solutions of 2n single-soliton.

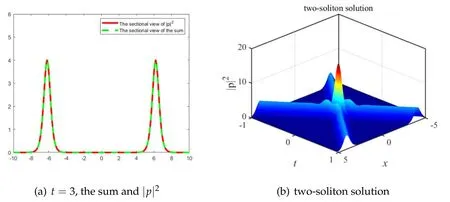
Figure 2.a1 = 1,b1 =1(a) The red solid lines represent the sectional view of ∣p[2] ∣2when t = 3.The green dotted lines represent the sectional view of the sum of the two decomposed single-soliton solutions with t = 3.It is shown that the sum matches ∣p[2] ∣2very well.(b) two-soliton solution: a1 = 2,b1 = 1, σ= -1.

Proof 6.We regard two adjacent matrix functions as a pair,and the expression of any pair is given as follows

From proposition 2 we know that if the parameters satisfy

then there is the following symmetric relationship betweenη(x,t)

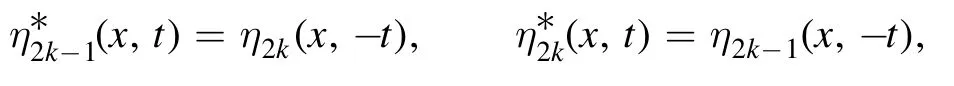
which yields that

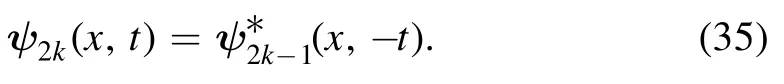
Choosing the2nparameters as follows

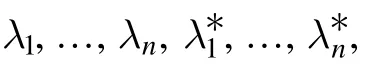
then the corresponding matrix functions could be listed out as follows

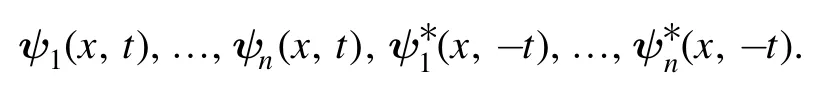
For each parameterλk=ak+ ibk(ak,bk∈R) we assume thatak＜ak-1＜ ... ＜a2＜a1＜ 0 (k≠1), andbk＜0.The two directions corresponding to any pair of matrix function,which is shown in equation (34), are

From lemma 3 we know that the square of the modulus of the soliton solution is symmetric about t,so below we only prove the situation whent→+∞.

Whent→+∞,fixed the direction asx+ 2a it=θ2i-1,we can deduce that

where

We can transform this determinant into the following easy-tosolve form [15]

where

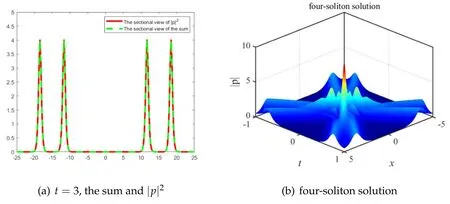
Figure 3.a1 = 1, b1 = 1, a2 = 3, b2 =1(a) The red solid lines represent the sectional view of ∣p[4] ∣2when t = 3.The green dotted lines represent the sectional view of the sum of the four decomposed single-soliton solutions with t = 3.It is shown that the sum matches ∣p[4]∣2 very well.(b) four-soliton solution: a1 = 2, b1 = 1, a2 = 3, b2 = 1, σ= -1.

and

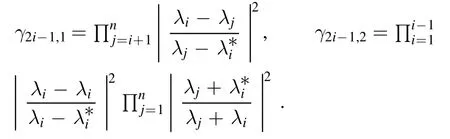
We can calculate that

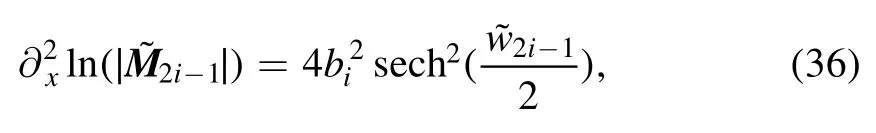
where

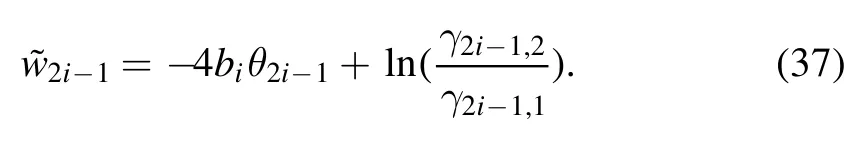
Similarly, if the direction is fixed asx- 2a it=θ2i, then we can derive that

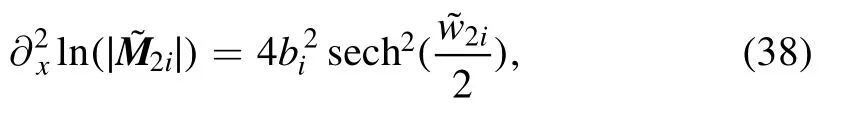
where

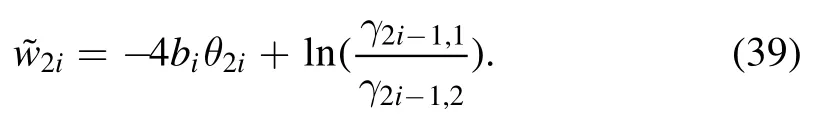
It must be noted that if the speed direction is fixed to any value other than the direction between any pair of matrix function, then we have

Combining the Lemma 3 and the results of equations (36),(38) and (40), we can finally infer that

where

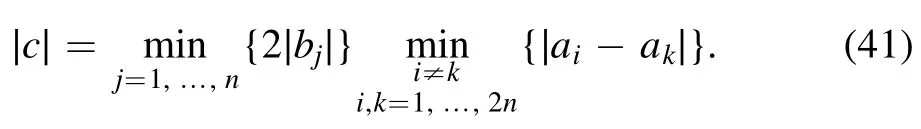
Example 3.Choosing the parameters asa1= 2,b1=1,a2= 3,b2= 1,σ= -1, we construct the asymptotic form of a four-soliton solution to test the result of theorem 3.Due to the symmetry of the solution with respect to the time variable t, here we only show the sectional view whent→+∞.Then results are shown in figure 3, which verifies the asymptotic analysis by numeric graphs.

Remark 2.For a(2n+1)-soliton solution, if the added parameterλ2n+1satisfies R(λ2n+1)=0, then the result still holds.

For theσ= 1, by setting the solution parameter ciof each matrix functionψi(x,t)asi,we can not only ensure the non-singularity of the soliton solution, but also obtain the sameM matrix as in the case ofσ= -1.So it can be similarly verified that

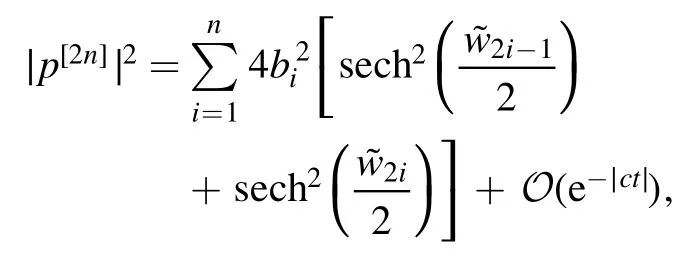
where

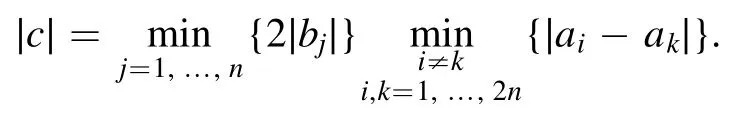
Remark 3.Compared to the classical NLSE, the asymptotic decomposition of the multi-soliton solutions of the nNLS equation under study is only applicable to the symmetric soliton solutions.In addition,the classical NLSE has not only the asymptotic expression of the square of the modulus of the solution,but also other forms of asymptotic expressions of the solution.What is more,there is no phase shift character inour asymptotic analysis, but in general it does existin classical NLSE.

4.Discussions and conclusions

In this work,we obtain and analyze the bounded multi-soliton solution for the focusing and defocusing nNLSE (1) in a uniform frame by the method of DT.Throughout the studies in this work,we find that the feature of soliton for the nNLSE is different from the classic NLSE in the following aspects.The amplitude of the soliton solution to the nNLSE is jointly determined by the spectral parameter and the solution parameter,but for the solitons of NLSE the amplitude of soliton is uniquely determined by the spectral parameter.The exponentially blow up and decay solution can admit the oscillating effect.And some special parameter setting will result in the singularity for the solutions, which can not appear for the solitons of classic NLSE.The bounded multi-soliton solutions also have the elastic interaction.These interesting dynamics would enrich the dynamics for the field of nonlinear physics.

We construct the N-fold DT for the nNLSE (1) by the loop group method.Then we use the DT to the determinant representation of multi-soliton solutions by zero seed solution.Afterwards, the singular and asymptotic analysis on multi-soliton solutions are performed by the formula of determinant.Actually, we propose a way to analyze the singularity and asymptotic analysis for the nonlocal type of NLS equation.This method can be readily extended to the multicomponent equation [26], two-place and four-place nonlocal integrable equation, multi-place nonlocal KP equation and so on.

As a matter of fact, there are lots of work to be performed.When constructing the solitonic solution, we only consider the zero seed solution.We can construct the solitonic solution by the plane wave solution or elliptic function seed solution.Meanwhile,the high order or the multi-pole solitons with large order are also deserved to study for these models.In addition, besides singularity and asymptotics, soliton solutions have many other noteworthy properties to be further explored.The above mentioned problems will be studied in the near future.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (Grant No.11771151), the Guangzhou Science and Technology Program of China (Grant No.201904010362), the Fundamental Research Funds for the Central Universities of China (Grant No.2019MS110).

ORCID iDs