分数阶拟周期Mathieu 方程的动力学分析1)

郭建斌 申永军 ,†,2) 李 航

* (石家庄铁道大学机械工程学院,石家庄 050043)

† (石家庄铁道大学交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)

引言

分数阶微积分第一次被数学家Hospital 与Leibnitz 提出,至今已有300 多年历史.起初,分数阶微积分因其缺乏应用背景在早期工程研究中并未得到广泛关注.1832 年,Liouville 首次将分数阶微积分用于解决一些实际问题.此后,众多学者在分数阶微积分的定义、性质和计算方法等方面展开了详细的探讨[1-6].在这个过程中,分数阶微积分也由数学理论研究逐步走向工程应用[7-11].

在控制工程领域,分数阶微积分主要用来影响系统的闭环控制特性,从而提高系统控制效果和鲁棒性.如薛定宇和赵春娜[12]提出了一种分数阶PID控制器的设计方法,具体演示了分数阶控制器对系统优良的控制效果.常宇健等[13]则针对含分数阶阻尼的悬架模型进行了主动控制研究.在动力学方面,分数阶微积分主要集中用于描述黏弹特性材料的本构关系,以此来提高此类非线性系统振动特性研究的准确性.如Cao 等[14]采用数值积分法,结合相图、庞加莱截面图、分岔图等分析了分数阶阻尼对系统动力学性能的影响.申永军等[15]通过对含分数阶线性单自由度振子的动力学分析,首次提出等效线性阻尼和等效线性刚度概念.申永军等[16-17]利用平均法得到分数阶van der Pol 振子的一次近似解,比较了分数阶与整数阶系统并分析了分数阶微分项对系统动力特性的影响.由上述研究可知,相比整数阶模型,分数阶模型的物理意义更清晰,更能准确描述实际系统.

Mathieu 方程作为一种周期系数线性微分方程,因其本身复杂的动力学特性,在动力学领域得到了广泛的应用[18-20],经常被用来处理一些参数共振现象.如Qian 等[21]研究了在参数激励和强迫激励作用下的斜拉桥拉索的非线性动力学问题,利用多尺度方法分析了1/2 参激共振下的动力学响应.黄建亮等[22]对van der Pol-Mathieu 方程的动力学特性进行了研究,应用改进的谐波平衡法精确计算出了方程的准周期响应.温少芳[23]研究了分数阶参激系统的动力学特性,分析了分数阶微分项对系统稳定性边界以及幅频响应的影响.同时,随着众多学者对Mathieu 方程的深入研究,促使其形式也得到了丰富拓展.Kovacic 等[24]对Mathieu 方程的推广型作了全面概述,包含拟周期系数和椭圆系数等多种形式的Mathieu 方程.其中,拟周期系数Mathieu 方程通常被应用于一些特殊的动力系统,如Galeotti 和Toni[25]提出的含双频激励时变刚度的高速列车受电弓非线性模型.Huan 等[26]研究了高速列车受电弓-悬链线组合系统中低频和高频参数激励对系统响应的影响等.Rand 等[27-28]则针对拟周期Mathieu 方程不同共振状态的稳定区域进行了深入研究.

综上所述,在含有黏弹性器件的参激系统(如弓网系统)中,分数阶模型较整数阶模型对系统描述更加准确.因此,本文在拟周期Mathieu 方程中引入分数阶微积分理论,建立了分数阶拟周期Mathieu 方程,利用摄动法求得了方程过渡曲线的近似解析解,通过数值方法在系统稳定图中分析了分数阶微分项参数对方程稳定区域大小和过渡曲线位置的影响,并验证了分数阶微分项同时含有阻尼和刚度特性的特点.

1 分数阶拟周期Mathieu 方程

1.1 摄动分析

本文研究的分数阶拟周期Mathieu 方程如下所示

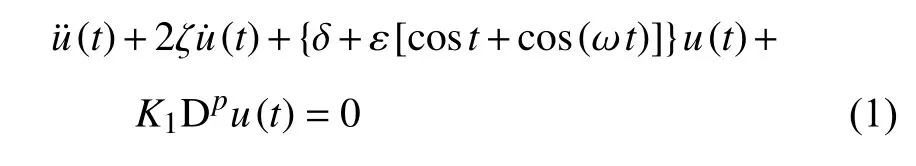
其中,ω 是无理数;ε 为小参数,满足| ε|≪1 ;2 ζ 和δ+ε[cost+cos(ωt)]分别为线性阻尼和时变刚度;Dp[u(t)]为u(t) 关于t的p阶导数 (0 ≤p≤1);K1为分数阶微分项系数 (K1＞0) .

关于分数阶微积分的定义有多种,这里采用Caputo 型分数阶微积分定义

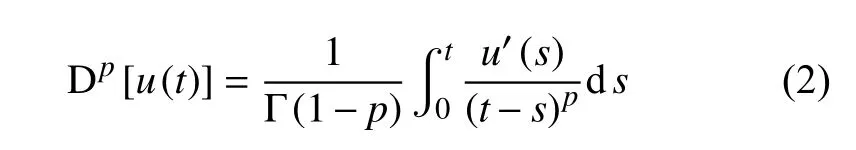
式中 Γ 为Gamma 函数,具有 Γ(z+1)=zΓ(z) 的特性.

为了确定方程稳态周期解的过渡曲线,引入ζ=εμ,μ=O(1),K1=εk,k=O(1),式(1)变换为

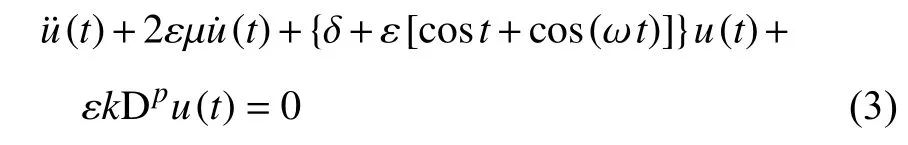
利用摄动法,假设式(3)的解满足

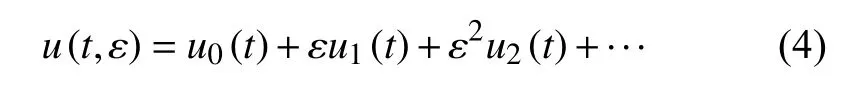
过渡曲线在 δ-ω 平面内具有如下形式

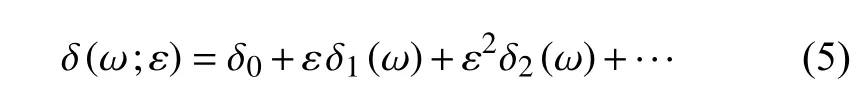
将式(4)和式(5)代入式(3),比较 ε 的同次幂得到

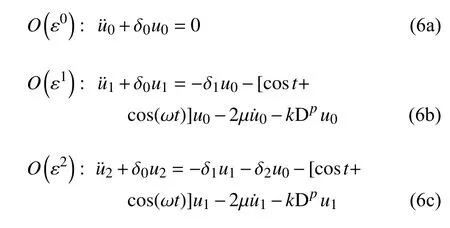
由式(6a)解得

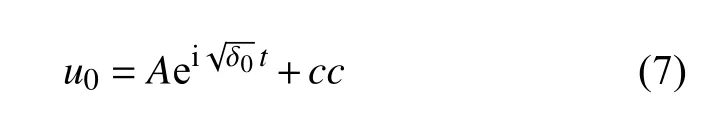
其中cc代表前面各项的共轭,后不赘述.由于 ω 是无理的,拟周期Mathieu 方程稳态周期解的过渡曲线在δ-ω平面上是从处产生[29],下面讨论方程在 α=0,1,β=-1,0,1 时的过渡曲线.

(1) δ0=0 (即 α=0,β=0)

根据式(6a)解得

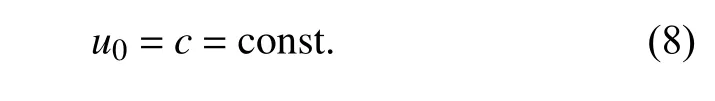
式中c是由初始条件确定的常量,将其代入式(6b)得到

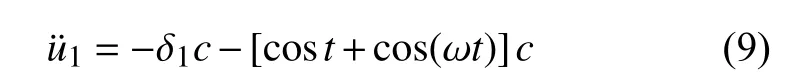
为了消除永年项需 -δ1c=0,所以有

则式(9)的特解为

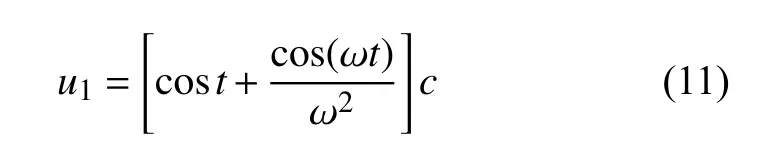
这里利用公式[30]对分数阶微分项kDpu1进行处理

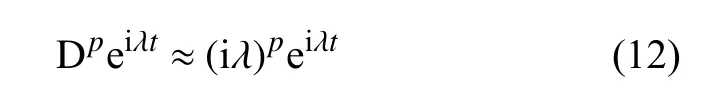
再结合欧拉公式得到

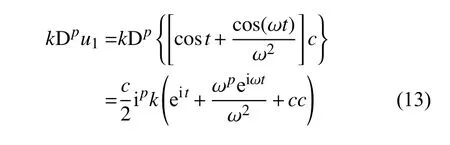
将式(8)、式(10)、式(11)和式(13)代入式(6c)得到

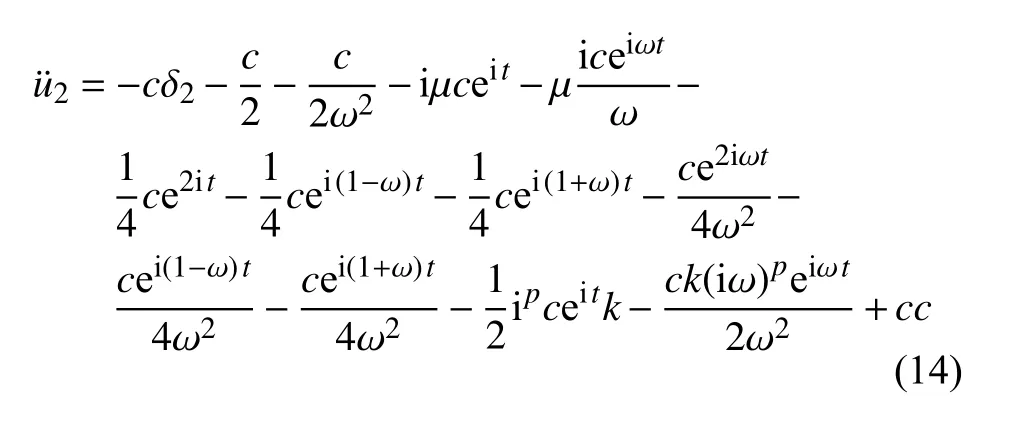
从上式得出消除永年项条件

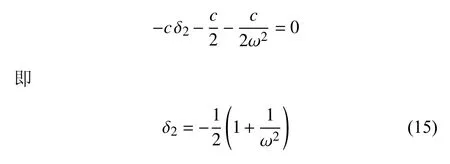
此时式(14)的特解为

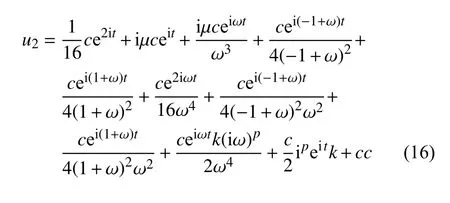
将式(10)和式(15)代入式(5)得到

分析式(17)可以看出,在 δ0=0 附近过渡曲线的二阶近似解与方程的分数阶微分项和阻尼都没有关系,所以进行三阶近似计算

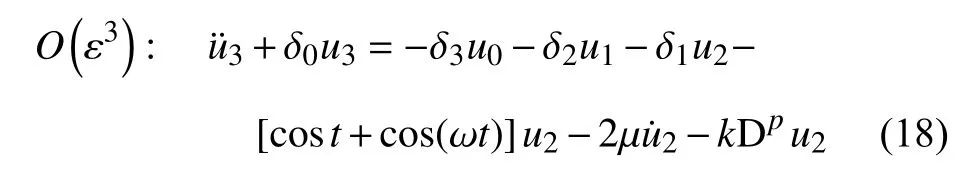
类似地,将式(8)、式(10)、式(11)、式(15)和式(16)代入式(18)可得到消除永年项条件

代入方程原参数得到 δ0=0 时过渡曲线的三阶近似解

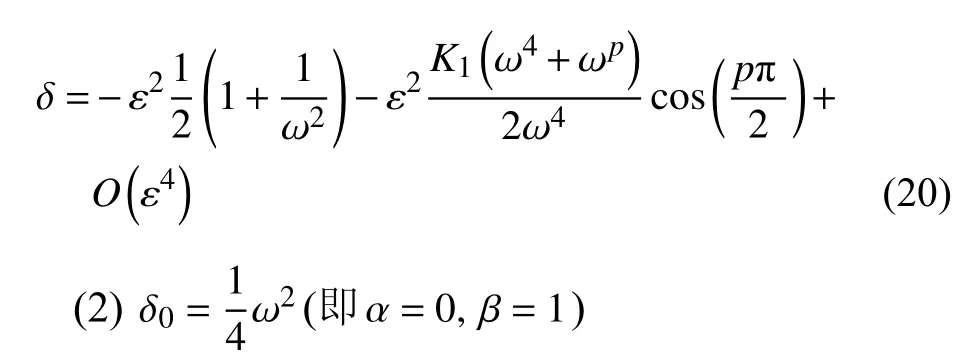
由式(7)得到式(6a)的特解为

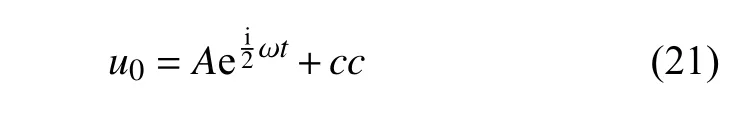
对分数阶项kDpu0进行处理得到

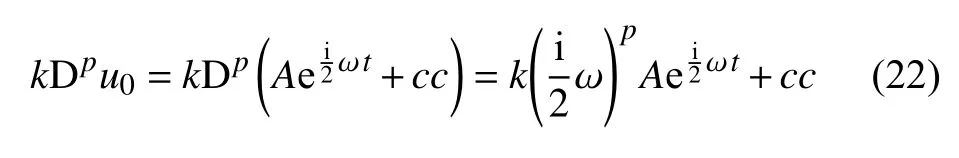
将式(21)和式(22)代入式(6b)中得到

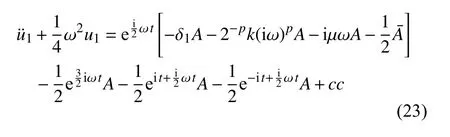
消除永年项条件为

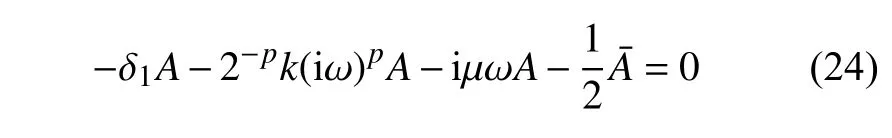
该方程有非零解的条件是

其中det 为求解矩阵行列式.计算得出

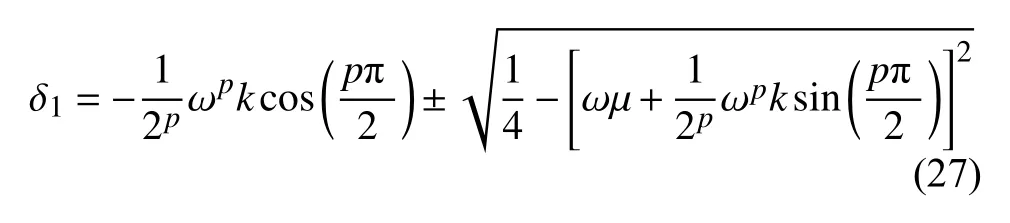
此时式(6b)的特解为

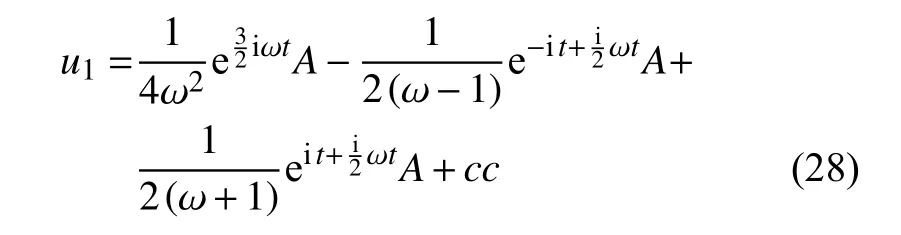
将式(21)、式(27)和式(28)代入式(6c)得

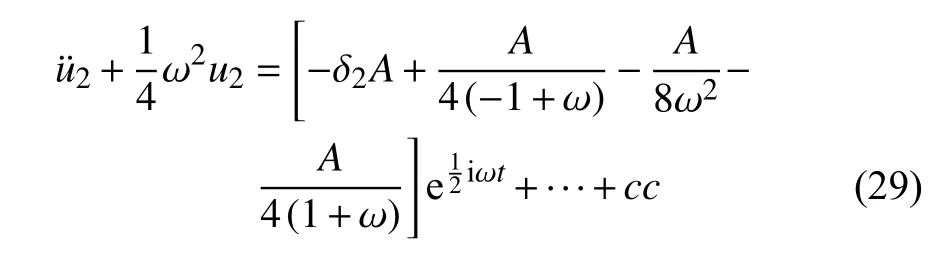
为了消除永年项,要求

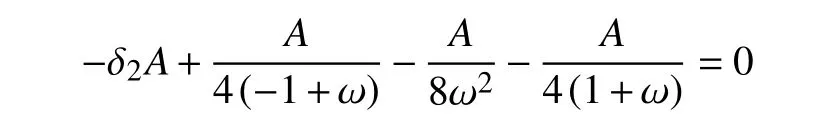
从而得到

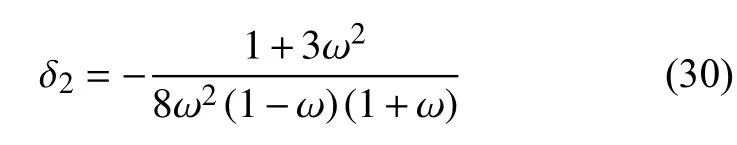
将式(27)和式(30)代入式(5),代入原参数整理得到此时的两条过渡曲线

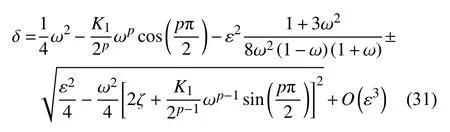
根据上述类似的计算方法相应求出β=0)时方程的过渡曲线为

1.2 方程过渡曲线分析

选取一组参数 ζ=0.005,K1=0.005,p=0.5,ε=0.1,利用式(20)和式(31)～ 式(34)并略去式中高阶部分绘制解析结果的过渡曲线如图1 所示.

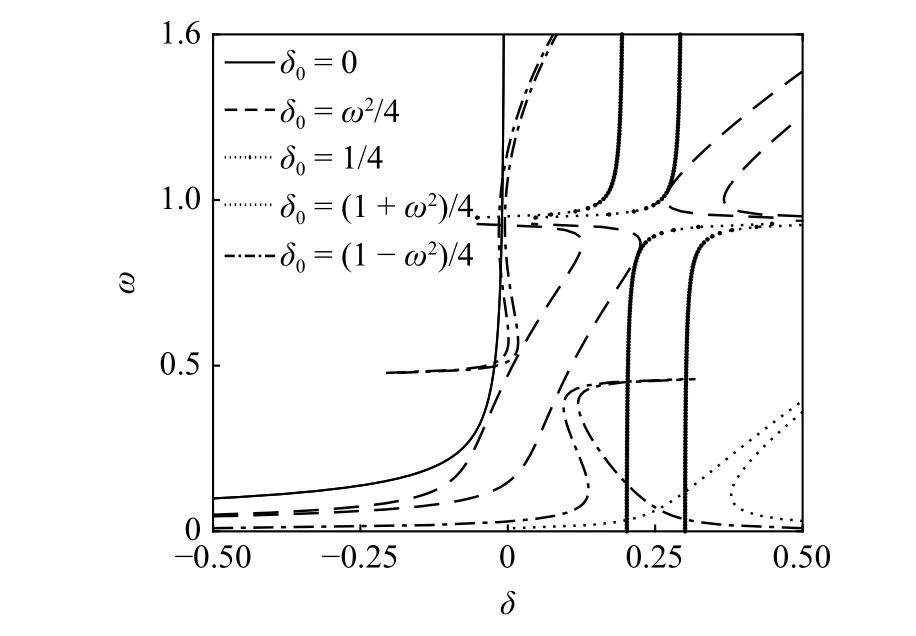
图1 分数阶拟周期Mathieu 方程的过渡曲线Fig.1 Transition curves of QP Mathieu equation with fractional-order derivative

对比不含分数阶微分项的Mathieu 系统[31-32],通过定义等效线性阻尼C(p) 和等效线性刚度K(p) 的方法来分析分数阶微分项对拟周期Mathieu 方程过渡曲线的影响. δ0在各情况下的等效线性阻尼和等效线性刚度如表1 所示.

通过表1,得到方程等效阻尼和等效刚度的一般形式

表1 δ0 在不同情况下的等效线性阻尼和等效线性刚度Table 1 Equivalent linear damping and equivalent linear stiffness of different δ0

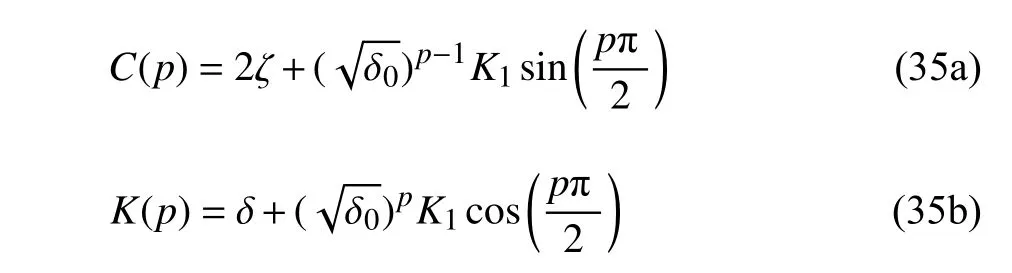
分析上述5 种情况下的结果可知,在 δ0=0 时,方程过渡曲线的二阶近似解与分数阶微分项无关,分数阶微分项以等效线性阻尼和等效线性刚度的形式影响着过渡曲线的三阶近似解.而在其他4 种情况中,分数阶微分项对方程二阶近似解均有影响,并且它们的等效线性阻尼和等效线性刚度均可整理为一般形式(35).通过分析式(35)发现,分数阶微分项的系数K1和阶次p对方程过渡曲线有着重要影响:当分数阶微分项系数K1逐渐增大时,等效线性阻尼和等效线性刚度都会逐渐增大;当分数阶阶次p趋近于0 时,分数阶微分项几乎等于线性刚度;而当p趋近于1 时,分数阶微分项几乎等于线性阻尼.

另外,通过对比式(31)～ 式(34)发现方程过渡曲线表达式具有一定的相似性,都是由 δ0开始随着ω的增大逐渐分裂成两条过渡曲线组成(δ=δ0+E±F),如方程在时过渡曲线式(31).根据这一特点,可以定义此时两条过渡曲线之间的厚度(即非稳定区域厚度)为

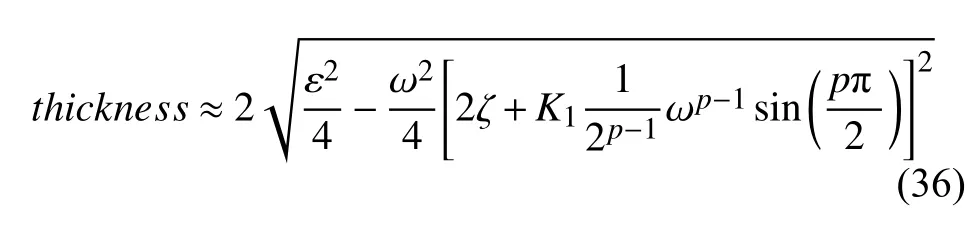
类似地,在 δ0为其他几种情况时也存在类似的式子来表示过渡曲线之间的厚度.利用式(36)可以更加直观地显示分数阶微分项系数和阶次的变化对δ-ω平面上非稳定性区域大小的影响.

2 数值仿真

2.1 数值解和解析解的比较

为了验证本文结果的正确性,下面将上述过渡曲线的解析结果和数值结果进行对比.利用文献[5]中介绍的数值方法研究方程(1),该方法的近似公式为

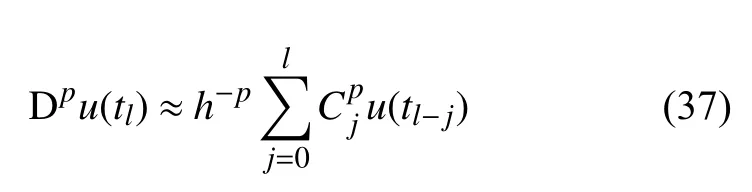
其中tl=lh为时间采样点,h为时间步长,为分数阶二项式系数,具有以下迭代关系

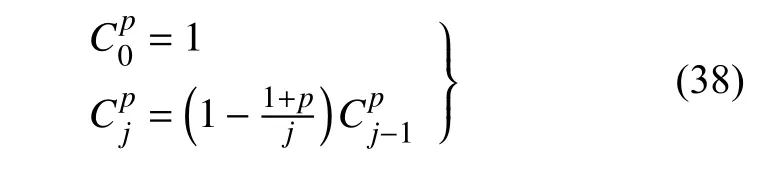
将 ω=0～1.5 和δ=-0.2～0.5 组成的δ -ω 平面内所有的点离散处理,分别代入式(1)中对方程进行数值积分,计算一段时间后根据方程响应的振幅变化情况判断各个参数点对应的稳定性,以此来确定式(1)的稳定区和非稳定区分界线.其中 δ 选择间隔为0.002,ω 间隔为0.01,计算时间为700 s,计算步长选择0.001,所得结果如图2 所示.仿真过程中参数取值为: ζ=0.005,K1=0.005,p=0.5,ε=0.1 .图中黑色的点代表数值解稳定点,白色是非稳定区域,白色和黑色的分界线是数值解的稳定性边界,红圈代表方程过渡曲线的解析结果.从图2 中可以看到方程在附近形成了指状的非稳定区域,且解析结果和数值结果的稳定性边界在主要区域吻合度较好,证明了文中所述方法和结果具有较好的准确性.

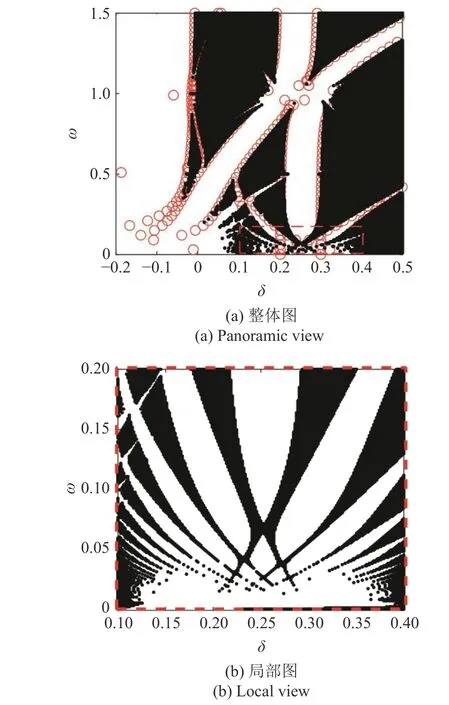
图2 数值解和解析解的方程过渡曲线Fig.2 Transition curves of numerical and analytical solutions

2.2 分数阶微分项对过渡曲线的影响

下面研究分数阶微分项参数对方程过渡曲线的影响.首先选定参数 ε,K1和 ζ,当分数阶微分项阶次p分别选取0.1,0.5 和0.9 时,方程在时的过渡曲线如图3 所示.

从图3 中可以看出,当分数阶微分项阶次p逐渐增大时,由于等效线性刚度K(p) 在逐渐减小,因此方程的过渡曲线在向右移动;同时,等效线性阻尼C(p)在逐渐增大,方程的非稳定区域在逐渐缩小.说明分数阶阶次p不仅影响方程过渡曲线的位置,而且还影响方程稳定区域的大小.

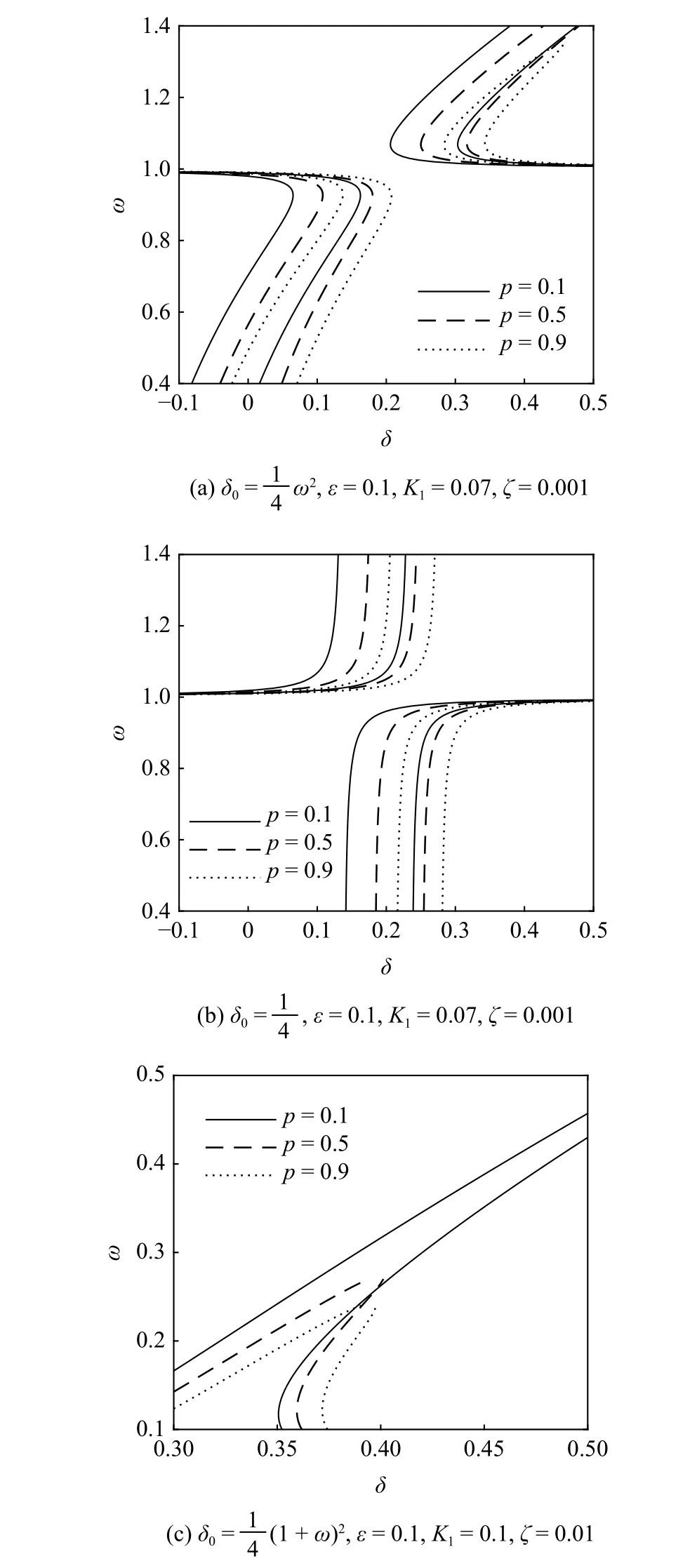
图3 分数阶微分项阶次 p 对过渡曲线的影响Fig.3 Effects of the fractional order p on transition curves

为了更好地区别分数阶微分项的阻尼和刚度特性,分别取分数阶微分项阶次p=0.1,p=0.5和p=0.9,观察不同阶次对方程过渡曲线的影响(ε=0.1,ζ=0.005),所得结果如图4～ 图6 所示.

图4 中给出了p=0.1 时方程过渡曲线随系数K1的变化情况.可以发现,当K1逐渐增大时,由于等效线性刚度也在逐渐增大,因此方程过渡曲线的位置发生了明显的左偏移;但此时等效线性阻尼变化较小,所以非稳定区域的面积未出现明显收缩.说明p=0.1时分数阶微分项呈现出较强的刚度特性,而阻尼特性相对较弱.

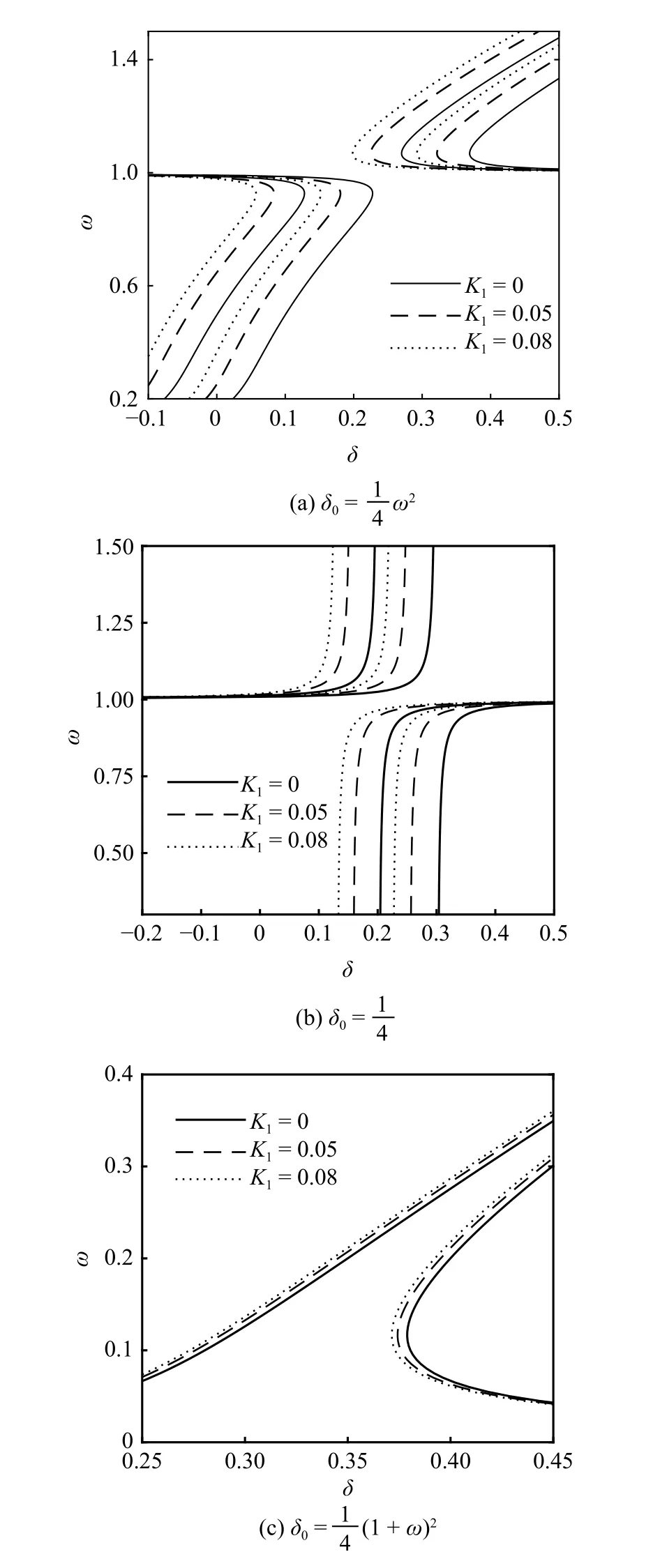
图4 p=0.1时分数阶微分项系数 K1 对过渡曲线的影响Fig.4 Effects of the fractional coefficient K1 on transition curves when p=0.1

当分数阶微分项阶次p=0.5 时,如图5(a) 和图5(b)显示,随着分数阶微分项系数K1的逐渐增大,此时等效线性刚度和等效线性阻尼都在增大,方程过渡曲线不仅逐渐向左偏移,同时曲线之间的厚度也在逐渐缩小.利用式(36) 观察时非稳定区厚度随系数K1的变化情况,从图5(c)看出,随着系数K1的逐渐增大,方程非稳定区面积在逐渐缩小,并且当系数K1增大到一定程度,发生了局部非稳定区域消失的现象.说明当p=0.5 时,分数阶微分项不仅具有明显的刚度特性还具有明显的阻尼特性.

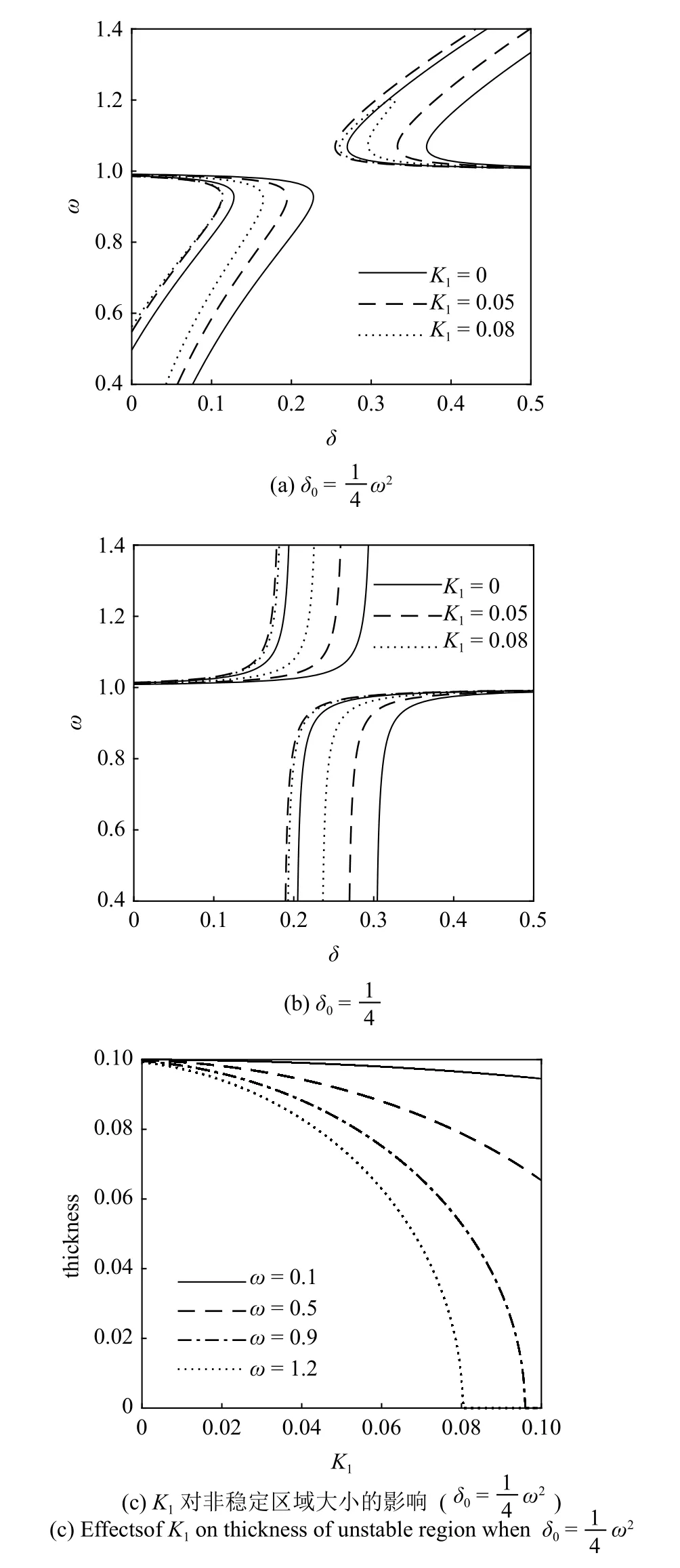
图5 p=0.5 时分数阶微分项系数对过渡曲线的影响Fig.5 Effects of the fractional coefficient on transition curves when p=0.5

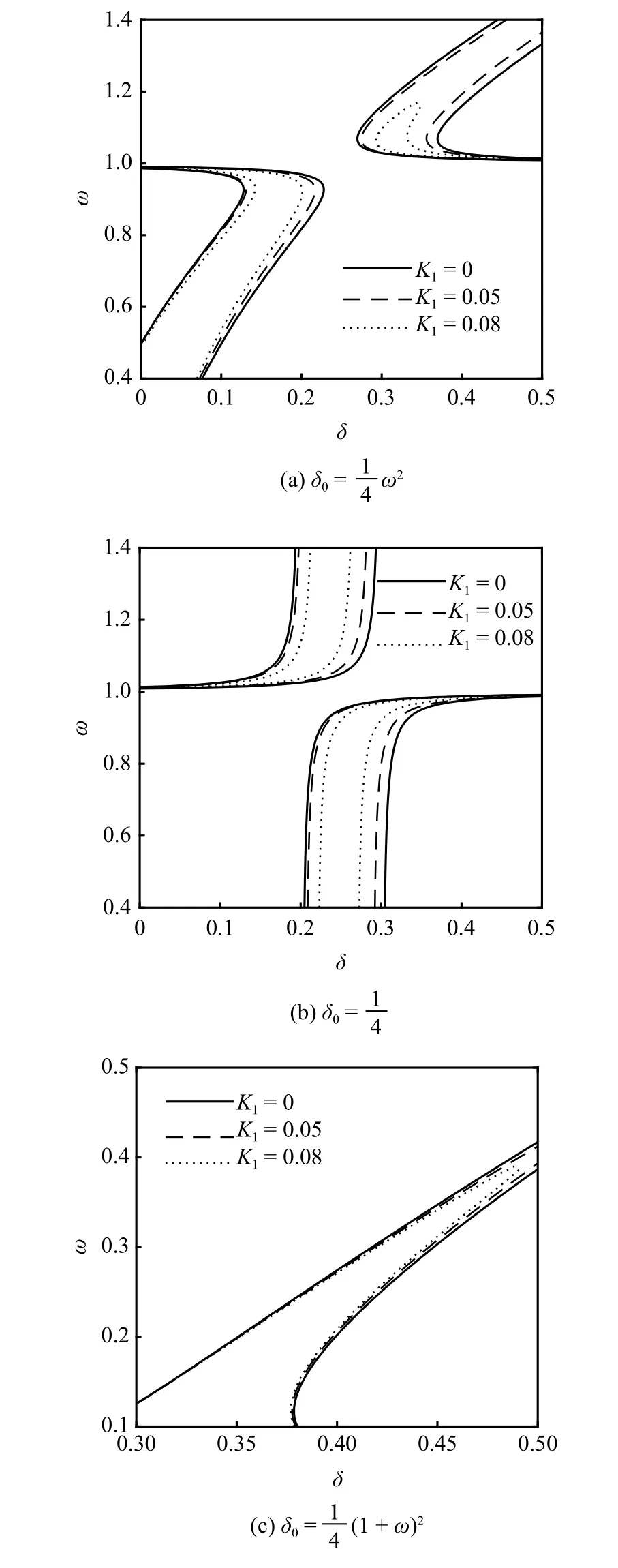
图6 p=0.9 时分数阶微分项系数 K1 对过渡曲线的影响Fig.6 Effects of the fractional coef0ficient K1 on transition curves when p=0.9

在图6 中分析p=0.9 时不同分数阶微分项系数K1对过渡曲线的影响.此外,为了便于比较,给出了p=0.5,K1=0.001时线性阻尼系数 ζ 对方程过渡曲线的影响情况,如图7 所示.由图6 和图7 可知,随着系数K1和 ζ 逐渐增大,方程的非稳定区域都发生了明显的收缩,说明此时分数阶微分项呈现出较强的阻尼特性,系数K1对系统的作用与线性阻尼系数 ζ 几乎相同.

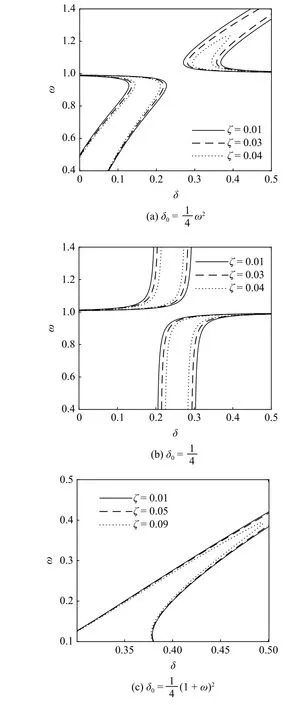
图7 线性阻尼系数 ζ 对过渡曲线的影响Fig.7 The evolutions of the transition curves due to the change ofζ

3 结论

应用摄动法研究了分数阶拟周期Mathieu 方程,得到了方程在 δ-ω 平面内过渡曲线的近似表达式.借助等效线性刚度和等效线性阻尼概念,分别分析了不同分数阶微分项系数和阶次对方程过渡曲线的影响.结果发现,分数阶微分项同时具有刚度特性和阻尼特性,选取不同的分数阶微分项阶次和系数可以使其呈现不同程度的刚度特性或阻尼特性,方程稳定区域的大小和过渡曲线的位置也因此产生了不同程度的变化.以上结果说明分数阶微分项对拟周期Mathieu 方程的稳定特性有着重要的影响,对此类系统的分析和稳定状态参数的选取有着重要的意义.