基于模态组合的短期负荷预测方法

苏 娟，方 舒，刘 博，杜松怀※，单葆国，高 天

（1.中国农业大学信息与电气工程学院，北京 100083；2.国网北京市电力公司朝阳供电公司，北京 100124；3.国网能源研究院有限公司，北京 102209）

0 引 言

短期负荷预测在电力系统的日运行调度工作中具有举足轻重的作用，可以有效协调发电、输电、配电、用电的关系[1]，对高比例可再生能源渗透下的电源灵活调节、电网高效联通、用户广泛响应的电力市场建设具有重要意义[2-3]。随着市场交易规模持续扩大，电力交易方式不断更新，清洁能源将广泛参与电力市场交易，电力负荷分析预测面临新挑战。

随着电力系统对负荷预测精度的要求越来越高，人工神经网络、支持向量机等机器学习方法因具有较强的学习和模拟能力，预测效果好等优点，得到广泛使用。最小二乘支持向量机（Least Squares Support Vector Machine，LSSVM）在支持向量机（Support Vector Machine，SVM）的基础上进行了改进，用平方差损失函数代替不敏感损失函数，将SVM的不等式约束变为等式约束，采用最小二乘线性系统作为模型的损失函数，待选参数少，简化了计算过程，提高了运算速度[4]，更适用于短期负荷预测。

对于波动性较强的负荷序列，单一的预测方法难以达到较高预测精度，组合预测方法得到广泛应用。对原始负荷序列进行分解，可以实现平稳序列和非平稳序列的分离[5]，降低预测过程中的干扰。国内外学者在基于负荷序列分解的短期负荷预测领域已开展了大量研究。文献[6]利用经验模态分解将负荷序列分解为多个独立的模态分量，利用多个指标分析各分量与影响因素的相关关系，总结构成各分量的不同负荷成分，使负荷特性分析更加深入细化；文献[7]采用经验模态分解的方法将负荷时间序列分解为频率成分不同的本征模态函数分量，然后利用LSSVM对各分量进行建模预测，将分量预测值叠加后得到最终的负荷预测值。但经验模态分解法难以避免模态混叠现象产生，分解得到虚假的本征模态函数，在预测时产生不利的影响。文献[8]利用小波分解算法对负荷曲线进行分解，对所分解出负荷中幅值较大的部分建立时间序列预测模型，对幅值较小的部分建立基于气象影响的神经网络预测模型，实例证明该方法可有效提升预测精度。但小波基函数和分解尺度主要受人为主观的影响，基本靠先前经验去选择，无法保证所选小波基函数和分解尺度对于当前负荷序列的合理性。文献[9]利用变分模态分解方法进行负荷序列分解，采用互信息理论量化影响因素与各负荷分量的相关度，最后利用深度信念网络对每个分量建立预测模型，可提升预测精度。变分模态分解将数据分解为特征互异的本征模态函数，减轻了模态混叠现象发生，有利于信号的进一步分析。

在负荷预测过程中，LSSVM中惩罚系数和核函数宽度基于经验选取，易增大预测误差。因此，需要考虑利用人工智能算法对预测模型进行参数优化。文献[10]利用布谷鸟搜索算法优化支持向量机，但布谷鸟搜索算法搜索速度慢；文献[11]利用粒子群的全局搜索能力克服了LSSVM 在选参时的不足；文献[12]采用粒子群算法对LSSVM的模型参数进行寻优，实现LSSVM参数的自动优化选取，单一的 LSSVM 很难做到准确地预测短期负荷；文献[13]采用LSSVM模型提高了SVM模型的学习能力和泛化能力，采用基于双种群的粒子群算法寻求混合核函数LSSVM模型的最优参数，结果表明预测精度明显提高。

本文提出了一种基于模态组合的短期负荷预测方法。首先，从真实性、独立性、有效性 3个方面，分别针对时域和频域的不同特点，提出了负荷序列和影响因素序列分解评价方法，并以评价指标最优为目标函数，利用粒子群优化算法优化变分模态分解参数；然后，以负荷的组合模态与待分析因素的相关性特征值最大为目标函数，通过遍历所有模态组合，寻找最优方案，将与负荷频域特性相似的影响因素模态序列进行组合，实现了影响因素的拓展；最后，将模态组合方法拓展出的影响因素变量作为粒子群优化最小二乘支持向量机（PSO-LSSVM）预测模型的输入变量，采用 2种预测组合策略进行短期负荷预测，并利用算例验证所提预测方法的有效性。

1 基于评价指标优化的改进VMD方法

在信号分解领域，变分模态分解（Variational Mode Decomposition，VMD）是目前应用较为广泛的方法之一[14]。相比于其他常规信号分解方法，VMD解决信号混叠问题的性能卓越。但目前对于VMD参数优化的研究存在优化维度不全面、优化方向不明确、优化方法过于主观等不足，无法满足高精度的负荷预测要求，需要进一步的深入研究。因此，本文提出一种基于评价指标优化的改进VMD方法。

1.1 VMD信号分解法

VMD整体框架为变分问题，以Wiener滤波、Hilbert变换、频率混合[15]为基础，可有效解决递归式分解方式所造成的包络线估计误差不断累积的问题[16]。VMD方法[17-18]通过寻求指定个数的本征模态函数（Intrinsic Mode Function，IMF），使各模态的估计带宽之和最小来构造变分问题，同时，利用交替方向乘子法更新模态的中心频率，对变分问题进行求解。

本征模态函数为一个调幅-调频信号，IMF的表达式为

式中Ak（t）为uk（t）的瞬时幅值，V；φk（t）为相位非递减函数，ωk（t）为uk（t）的瞬时频率，Hz。Ak（t）及ωk（t）相对 于φk（t）是 缓 变 的 ， 即 在[t-δ,t+δ]（ 其 中δ=2π //（t））的时间间隔内，u（t）可以看做是一个幅k值为Ak（t）、频率为ωk（t）的谐波信号。

1.2 改进的信号分解评价指标

目前在负荷预测领域对信号分解质量的评价指标主要集中在时域层面，然而频域中体现出的信号分解效果同样重要。因此，本文综合考虑时域、频域 2个维度在信号分解评价中的突出特点，量化描述 2个维度在信号分解真实性、独立性、有效性 3个方面的影响程度，建立改进的信号分解评价指标。

1.2.1 真实性检验

对信号分解的真实性检验包括冗余分量检验与残差分量检验2部分，若某信号分解方法同时通过上述2个检验，则认为此分解方法信号分解通过真实性检验，可以进行后续评价指标的计算；若只通过 1种检验或是 2种检验均未通过，则该方法不满足真实性检验的要求，说明其信号分解效果差，不宜采取。

1）冗余分量的真实性检验。

冗余分量真实性检验针对时域分解信号进行评价，采用分量信号与原始信号的皮尔逊相关系数[19]与真实性阈值的对比，公式如下：

式中｛x1,x2,...xn｝、｛y1,y2,...yn｝为2组长度为n的数据序列，、分别为2组数据序列的平均值。

冗余分量真实性检验通过的条件为 ∀fi,ρ（fi,fo）＞rre。其中fo为原始信号，fi, （i= 1 ,2,...,K）为分解出的分量信号，K为分量信号总数，ρ（fi,fo）为分量信号fi与原始信号fo的皮尔逊相关系数，rre为相关性阈值。

2）残差分量的真实性检验

残差分量的真实性检验的定义是残差分量与原始信号数据序列的二范数比例衡量信号的能量占比。本文从频域来评价分解信号的真实性，利用残差频谱中幅值显著的频段在原始信号频段中的比例衡量残差分量的频谱特性。残差分量真实性检验通过的条件为。其中fe为残差分量，n o rm （fe）为残差分量数据序列的二范数， n orm（fo）为原始信号数据序列的二范数，ren为能量占比阈值；lo为原始信号的显著频谱长度，ler为残差频谱中的显著频段长度，rfr为残差频段占比阈值。

1.2.2 独立性评价指标

每一个信号分量分别对应原始信号中某一独特的特征信息，相互独立的信号分量之间信息交叉少，可提供较为纯粹的特征信息，因此信号分量的独立性是评价信号分解质量的重要参考依据。本文利用信号分量两两之间的平均皮尔逊相关系数I1和显著频段平均重叠度I2这2个指标，在时域和频域2个维度对信号分解的独立性进行评价。平均皮尔逊相关系数I1计算公式如下：

显著频段平均重叠度I2的计算公式如下：

式中=lij/（li+lj）， （i,j∈ 1 ,2,...,K;i≠j），代表分量信号fi与fj的显著频段重叠度，li、lj分别为fi与fj的显著频段长度，lij为fi与fj重叠的显著频段长度。I2的数值越小，信号分解方法的频域独立性表现越好。

1.2.3 有效性指标检验

有效性评价指标用于评价分解出的各分量信号所携带有效信息的质量。高质量的分量信息携带原始信号中较多且集中的特征信息，其在时域中体现出与原始信号的相关性更强，因此，采用各信号分量与原始信号的平均皮尔逊相关系数I3来衡量有效性的时域特性，公式如下：

同时，高质量的信号分量在频域中体现出频谱更为密集的特点，采用分量信号显著频段的平均集中度指标I4对其进行量化：

式中lf为信号的频域长度，lsec为第一个显著频率与最后一个显著频率之间的频段长度。I4的数值越小，信号分解方法的频域有效性表现越好。

1.2.4 综合评价指标

针对独立性评价的时域、频域指标以及有效性评价的频域指标，指标数值越小，特性表现越好。但有效性评价的时域指标I3却表现出相反的性能，为了统一指标的性能方向，在综合评价指标中对I3进行反向处理，采用=1-I3作为新的有效性评价时域指标，使4个指标的性能方向一致，且4个指标的取值范围均在0～1之间，不存在数据量级不统一带来的数据遮蔽问题。综合评价指标Ic由这4个指标相加得到，公式如下：

综合评价指标的数值越小，信号分解效果越好。需要注意的是，综合评价指标的使用前提为通过真实性检验。

1.3 基于评价指标优化的改进VMD方法

VMD方法中涉及的参数有4个，分别为模态分解总数K，二次项惩罚因子α、拉格朗日乘子保真度τ和判别精度e[20]。其中判别精度参数对分解结果的影响较小。另外 3个参数对信号分解的效果影响较大，需要对其进行优化。本文以信号分解的综合评价指标为目标函数，利用粒子群优化算法对 3个参数进行优化，建立基于评价指标优化的VMD方法。

粒子群优化算法[21-22]（Particle Swarm Optimization ，PSO）的原理表述如下：首先，在可行域的范围内初始化一群随机粒子，在每一次迭代中，每个粒子通过2个极值来更新自己的速度和位置：个体极值pbest和全局极值。个体极值是单一粒子曾经经过的最优位置，全局极值是粒子群中所有粒子曾经经过的最优位置。通过多次迭代搜索优化问题的最优解。

粒子群的进化公式如下：

式中w为惯性权重；c1、c2为加速因子；r1,r2∈ R and[0,1]，用以保证算法的不确定性；分别为第k次迭代中第i个粒子的速度、位置、个体极值最优位置和群体极值最优位置。

2 基于模态组合的PSO-LSSVM短期负荷预测模型

在以往的负荷预测建模中，通常将影响因素的原始序列作为影响因素变量直接加入到模型的输入中。但上述做法并未挖掘影响因素序列中隐含的特征信息，存在数据利用效率低的问题。因此，本文利用模态组合的方法对负荷预测的影响因素序列进行预处理，充分挖掘隐含的特征信息。同时，采用最小二乘支持向量机（LSSVM）作为预测算法，利用粒子群优化算法（PSO）优化LSSVM的参数。

2.1 模态组合的基本方法

每一个模态序列都对应原始序列的某种特征信息，将模态序列进行组合，可以挖掘出更多的隐含特征。依据特征条件将携带相似特征信息的模态进行组合，实际上是对原始序列的有效分割。模态组合方法主要包含特征提取、模态组合2部分。

2.1.1 特征提取

1）时域特征提取

在概率论和信息论的领域中，互信息（Mutual Information）是一种有效的信息度量，描述一个随机变量中所包含另一个随机变量信息量的大小，是 2个随机变量之间相互依赖程度的度量。不同于皮尔逊相关系数只能反映变量之间的线性相关程度，互信息利用熵的概念，既可以衡量变量之间的线性相关性，也可以衡量变量之间的非线性相关性[24]，故本文采用互信息作为时域特征提取方法，互信息计算公式如下：

式中I（X,Y）为变量X、Y的互信息，n为变量X中的元素个数，m为变量Y中的元素个数，p（xi）、p（yj）分别为xi、yj元素出现的概率，p（xi,yj）为xi、yj共同出现的概率，I（X,Y）数值越大，X、Y的相关性越高。

2）频域特征提取

经改进的 VMD方法分解所得的各模态序列之间相互独立，各模态的频谱带宽紧凑。因此，本文取各模态频率中心所对应的模态周期作为各模态的频域特征，计算公式如下：

式中fi为各模态的中心频率，Hz；iT为各模态的中心频率所对应的模态周期。

2.1.2 模态组合

模态组合是通过模态数据序列求和的方式，将多个模态序列整合成为一个组合模态序列。各个组合模态序列相加后可以得到原始的数据序列，符合数据的完整性原则。模态组合方法的流程图如下图所示：

2.2 基于模态组合的影响因素处理

为充分挖掘影响因素序列中隐含的特征信息，本文利用模态组合的方法，将与负荷频域特性中体现出相似周期性的影响因素模态序列进行组合。组合之后，影响因素数目由一个拓展到多个，影响因素的数目与负荷频域特性的显著频段个数相同，且组合后的影响因素模态与相应的负荷序列具有更强的相关性。

由于短期负荷预测的预测对象为日负荷，结合前期采用小波分析、评价指标优化的集合经验模态分解法（Ensemble Empirical Mode Decomposition，EEMD）、VMD法等分解算法对大量负荷序列的分解结果得出，分解后的负荷频谱主要在 3个频段内呈现较高的周期性：周期大于24 h（不包括24 h）的负荷，体现在日期类型（如工作日、节假日）的周期变化，可以近似描述短期负荷的趋势性；周期为12～24 h（不包含12 h）的负荷频段，体现了1 d内用电习惯（如昼夜交替、日前电价）的变化，可以近似描述负荷的波动性；小于12 h的负荷频段，体现了用户在1 d内用电的随机性（如天气、电价不确定性对负荷的影响），可以近似描述负荷的随机性和不确定性。根据以上分析，本文对上述影响因素拓展方法进行如下简化：

1）将影响因素模态序列中周期变化大于24 h（不包含 24 h）的模态进行组合，组合模态作为影响因素趋势分量，对应描述负荷的趋势性；

2）将影响因素模态序列中周期变化为12～24 h（不包含 12 h）的模态进行组合，组合模态作为影响因素波动分量，对应描述负荷的周期波动性；

3）将影响因素模态序列中周期变化小于12 h的模态进行组合，组合模态作为影响因素随机分量，对应描述负荷的随机性与不确定性。

2.3 基于模态组合的PSO-LSSVM短期负荷预测方法

支持向量机方法具有较强的泛化能力，在寻找全局最优中有较大优势。但考虑到支持向量机方法在参数设定方面存在不足，本文采用最小二乘支持向量机（LSSVM）作为预测算法，并利用粒子群（PSO）优化算法优化LSSVM的参数。

2.3.1 LSSVM基本模型

最小二乘支持向量机[25-27]（LSSVM）是支持向量机（SVM）的一种变形，保留了传统的支持向量机结构风险最小的特性[28]。将支持向量机优化模型中的不敏感损失函数设定为最小二乘损失函数，用等式约束替代不等式约束，减少需优化的参数个数，降低了求解复杂度[29-30]。

LSSVM的非线性函数式如下式所示：

式中k（x,xi）取不同的核函数就可生成不同的支持向量机。目前使用最多的核函数主要有多项式核函数、线性核函数、径向基函数（Radial Basis Function，RBF）。其中，RBF核函数结构简单，泛化能力强，仅核函数σ与正规化参数γ需进行优化。

2.3.2 适应度函数设置

粒子群优化算法中的每个粒子包含3个维度，分别代表需要优化的3个参数，本文利用粒子群算法优化LSSVM的核参数σ和正规化参数γ，适应度函数为

式中N为样本数量；Pij、Rij分别为第i个样本第j维观测数据的预测值和真实值。

2.3.3 基于模态组合的 PSO-LSSVM 短期负荷预测方法

传统的模态预测方法（以下称原始模型）是将各影响因素的整体序列作为模型的输入变量，得到负荷整体预测值。基于模态组合的预测方法在预测组合策略上主要分为 2种，一种是建立组合预测模型（以下称组合模型），即分别利用各个影响因素的趋势分量、波动分量、随机分量预测负荷的趋势模态、波动模态和随机模态，得到负荷各模态的预测值之后，再将其加和得到最终的预测结果。另一种是仅建立一个预测模型（以下称单一模型），将所有影响因素的趋势分量、波动分量、随机分量均作为模型的输入变量，直接得到最终的预测结果。

2种预测策略各有优势，建立组合预测模型的策略中，各影响因素分量与对应的负荷模态有更强的相关性，单个模型的预测精度可以得到有效保障。但由于多个预测模型预测值的叠加会累积预测模型本身存在的固有误差，可能无法满足短期负荷预测对预测精度的要求。直接预测最终负荷的预测策略，由于仅建立单个预测模型，因此不存在模型固有误差的叠加，但可能存在重复性输入的问题，需进行降维处理[31-32]。

将得到的影响因素拓展变量输入PSO-LSSVM模型，即可得到预测日的负荷预测值。输入变量主要包含历史负荷、温度、湿度、日前电价的原始序列，拓展出的分量序列以及经降维后的主成分序列，具体如下：

1）温度。预测日当天、预测日前1 d、预测日前2 d的温度原始序列、趋势分量、波动分量与随机分量；

2）湿度。预测日当天、预测日前1 d、预测日前2 d的湿度原始序列、趋势分量、波动分量与随机分量；

3）历史负荷。预测日前一周同时刻、前1 d同时刻、前1 d前一时刻的负荷原始序列、趋势分量、波动分量、随机分量；

4）日前电价。预测日当天的日前电价原始序列、趋势分量、波动分量、随机分量；

5）主成分序列。针对影响因素的重复输入，将降维后的主成分序列作为输入变量。

3 实例验证

为验证上述所提基于模态组合的短期负荷预测方法的有效性，本文以美国新英格兰地区 2016年全年 8760点实测负荷数据为数据源，利用基于评价指标优化的变分模态方法对负荷序列进行分解，以验证基于评价指标优化的变分模态分解方法的有效性。同时，选用新英格兰地区2016年1月2日-2月29日冬季以及2016年7月1日-8月31日夏季的工作日负荷、日前电价、温度、湿度数据为数据源进行算例分析，以验证模型预测的精度。

3.1 基于评价指标优化的变分模态分解结果分析

3.1.1 分解结果分析

利用基于评价指标优化的变分模态分解方法对上述负荷序列进行自适应的信号分解，分解后的各模态时序图以及各模态的频谱图如图2、图3所示：

由图2可知，本文方法分解出了3个模态分量，本征模函数（Intrinsic Mode Function，IMF）IMF1的能量占比最大，但波动性较小，与原始负荷序列表现出相同的变化趋势，夏季负荷水平较高，且负荷差最大；IMF2的波动性较强，尤其在夏季时段最为显著；IMF3的能量占比最小，但波动性最强，而其夏季时段（5 000 h左右时段对应7、8月）的波动性较弱。残差分量的数值主要在-2～2间波动，在原始信号中的能量占比为 0.011%，几乎可忽略不计。

从图3中可以看出，IMF1的频段主要集中在1.649e-6Hz左右，IMF2的频段主要集中在1.157e-6Hz，IMF3的频段主要集中在2.315e-5Hz，残差分量无明显频段特征。IMF1的显著频段对应的模态周期为大于24 h（不包含24 h），IMF2的显著频段对应的模态周期为12～24 h（不包含 12 h），IMF3的显著频段对应的模态周期为小于 12 h，残差没有显著频段。且各模态之间未出现明显的频段重叠。由此可见，本方法能够提取出原始序列中周期性较强的模态分量，信号分解的质量也较高。

3.1.2 与其他方法的比较分析

为验证本文方法的有效性，将小波分析[33-34]、集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）[35]、VMD这3种在负荷分解中应用效果较好的信号分解方法进行比较分析。小波分析，利用小波函数db3（Daubechies，db），取分解层数为1～10，对相同数据源进行分解，选取效果最好的分解结果作为对比，最优的分解层数为3层，得到4个信号分量。评价指标优化的EEMD方法，利用PSO优化2个主要参数：白噪声序列幅值系数k以及执行经验模态分解（Empirical mode decomposition，EMD）的总次数M，以综合评价指标最优为适应度函数，将原始数据序列自适应地分成了12个分量。未经优化的VMD，对相同数据集进行分解，分解出了 4个模态分量。各分解方法的指标对比结果如表1所示。

从表1中可以看出：在4种信号分解方法中，小波分析未通过真实性检验，其他2种方法均通过了真实性检验；优化后的VMD方法综合评价指标比优化后的EEMD方法小 0.989；优化后的 VMD方法综合评价指标比未优化的VMD方法小0.155。由此可见，本文所提信号分解方法在实际应用中具有明显优越性。

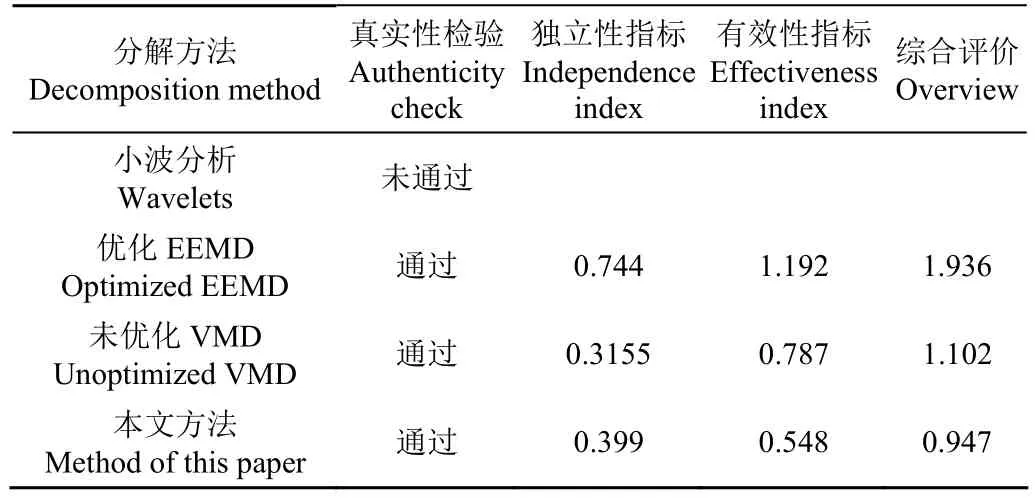
表1 不同信号分解方法的指标对比Table 1 The index comparison of different signal decomposition methods

3.2 基于模态组合的影响因素拓展

以美国新英格兰地区2016年1-2月份的工作日负荷、日前电价、温度、湿度数据为数据源，进行负荷结构辨识与影响因素拓展的算例分析。数据样本为每日24个数据点，共计960个样本点。

3.2.1 气象因素拓展

经VMD分解后的温度和湿度的时序图如图4、图5所示：

考虑到温度、湿度的累积效应，利用模态组合的方法对预测日前2 d、前1 d以及当天的气象因素进行组合，组合结果见表2～表3。

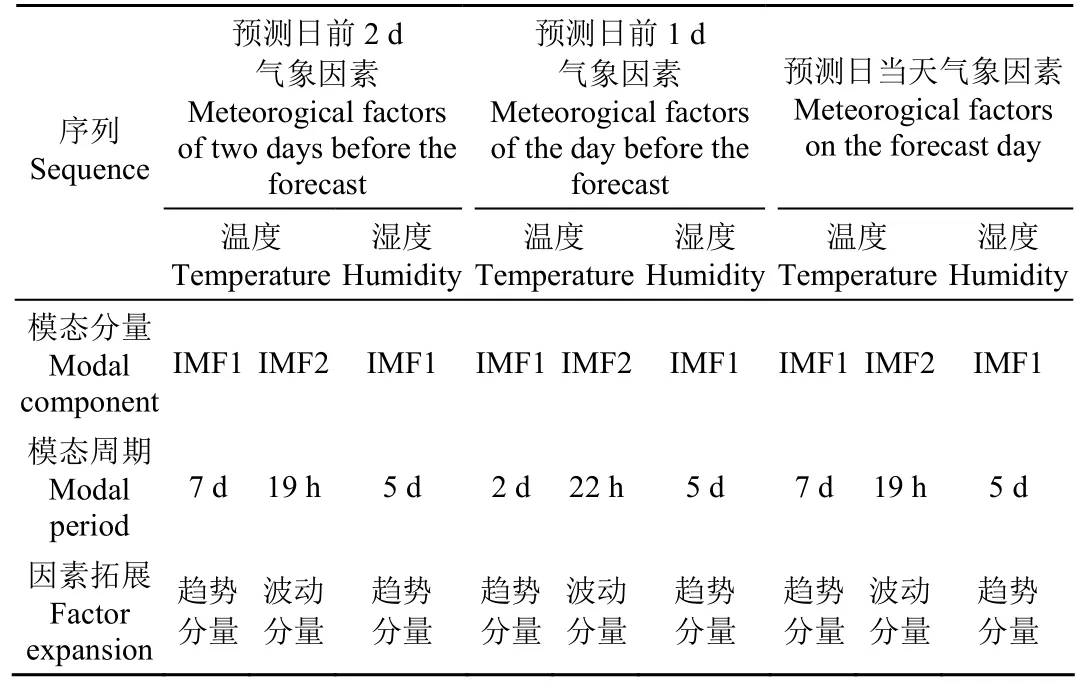
表2 气象因素的组合结果Table 2 Combination of meteorological factors

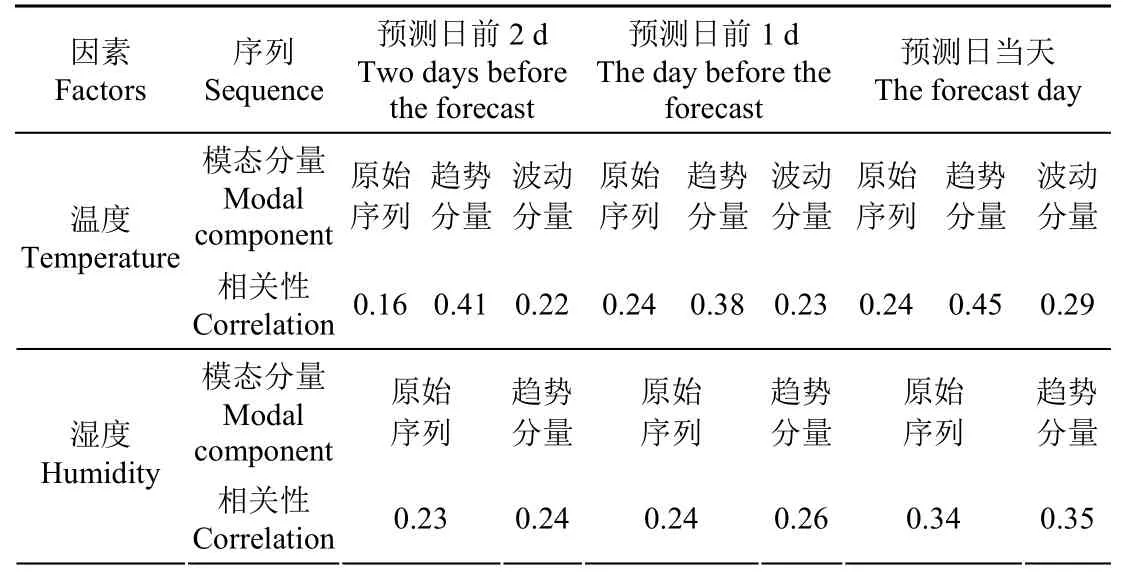
表3 模态组合因素与预测日负荷的相关性Table 3 Correlation between modal combination factors and forecast daily load

从表2可以看出，通过模态组合的方法，预测日前2 d温度、预测日前1 d温度、预测日当天温度均被拓展成了2个，分别为温度趋势分量与温度波动分量；湿度因素由于只存在 1个模态，没有组合出更多的因素分量。

从表3可知，预测日前2 d温度因素拓展出的趋势分量和波动分量与负荷的相关性分别比原始序列高 0.25、0.06；预测日前1 d温度因素拓展出的趋势分量与负荷的相关性比原始序列高 0.14，波动分量低 0.01；预测日当天温度因素拓展出的趋势分量和波动分量与负荷的相关性分别比原始序列高0.21、0.05。预测日前2 d湿度因素拓展出的趋势分量与负荷相关性比原始序列高 0.01；预测日前 1 d湿度因素拓展出的趋势分量与负荷的相关性比原始序列高 0.02；预测日当天湿度因素拓展出的趋势分量与负荷的相关性比原始序列高 0.01。由此可见，基于模态组合的方法不仅使影响因素的数目得到拓展，而且组合出的因素分量与负荷的相关性更高，有利于提升预测模型的精度。

3.2.2 历史负荷因素的模态组合

由于负荷自身的周期性，历史负荷也是常见的负荷预测影响因素变量。选取预测日前 1周同时刻负荷、预测日前1 d同时刻负荷、预测日前1 d前一时刻负荷作为历史负荷因素，并利用模态组合的方法研究影响因素，结果如表4、表5所示。

从表4、表5可知，预测日前1周同时刻负荷、预测日前1 d同时刻负荷、预测日前1 d前一时刻负荷的原始序列均被拓展成了 3个分量，分别为趋势分量、波动分量、随机分量。预测日前 1周同时刻负荷拓展出的趋势分量、波动分量和随机分量与负荷的相关性分别比原始序列高0.34、0.55、0.27；预测日前1 d同时刻负荷拓展出的趋势分量、波动分量和随机分量与负荷的相关性分别比原始序列高0.43、0.48、0.26；预测日前1 d前一时刻负荷拓展出的趋势分量、波动分量和随机分量与负荷的相关性比原始序列高0.52、0.56、0.19。

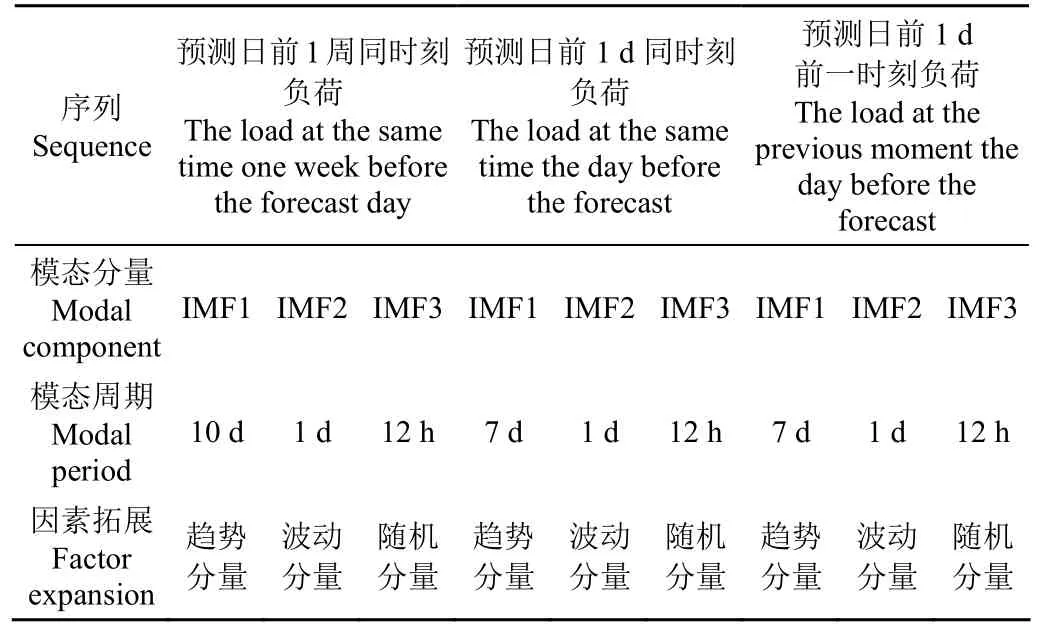
表4 历史负荷因素的组合结果Table 4 Combination results of historical load factors

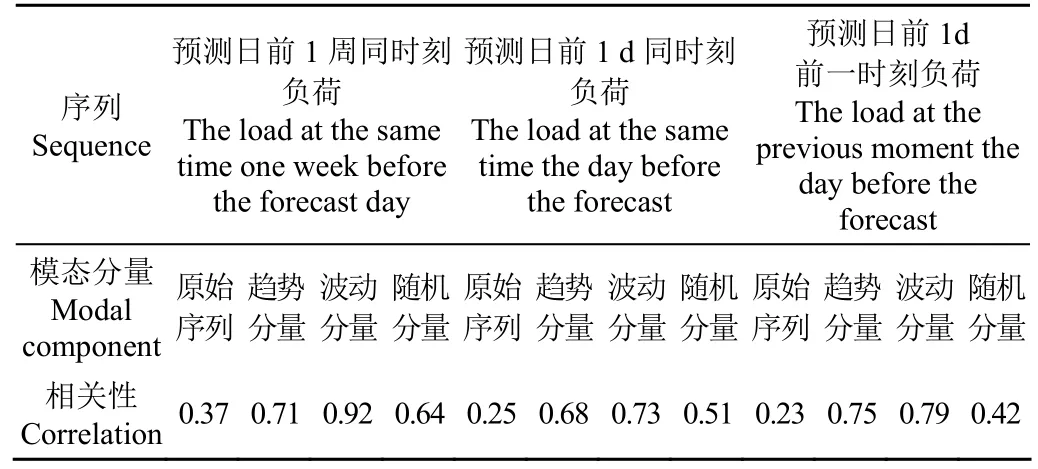
表5 模态组合历史负荷因素与预测日负荷的相关性统计Table 5 Correlation statistics between historical load factors of modal combination and forecast daily load

3.2.3 经济因素拓展

日前电价分解后的时序图如图6所示。

利用模态组合的方法对日前电价因素进行组合的结果见表6、表7。

由表6、表7可知，日前电价因素被拓展成了3个因素分量，IMF1构成了趋势分量，IMF2构成了波动分量，IMF3、IMF4、IMF5共同构成了随机分量。拓展之后的分量中，趋势分量与预测日负荷的相关性为 0.70，波动分量与预测日负荷的相关性为 0.78，高于原始序列与预测日负荷的相关性。随机分量的相关性为 0.43，虽不如原始序列与负荷的相关性高，但也具有较强的相关性。

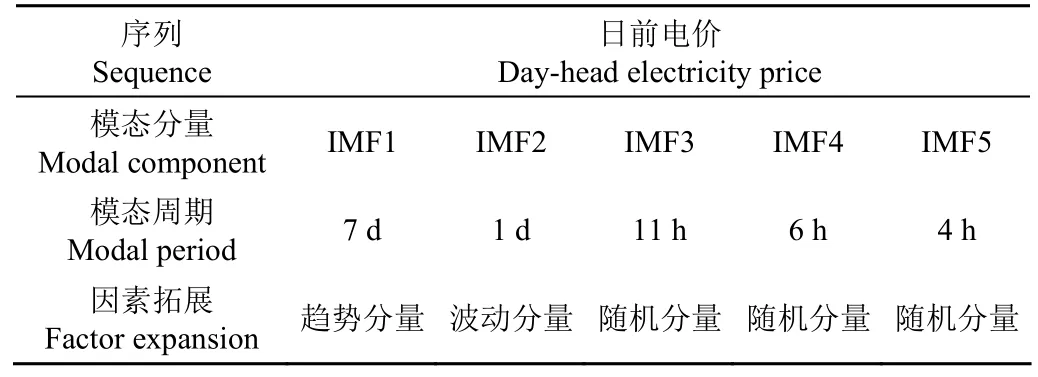
表6 日前电价因素的组合结果Table 6 Combined results of the previous electricity price factors

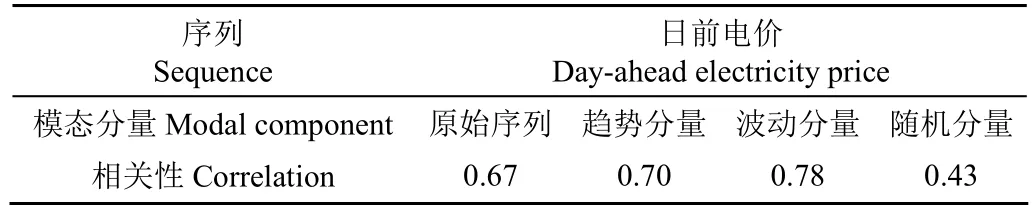
表7 模态分解的日前电价因素与预测日负荷的相关性统计Table 7 Correlation statistics between day-ahead electricity price factors and forecast daily load based on modal decomposition

日前电价中IMF3与负荷的相关性为0.33，IMF4与负荷的相关性为0.26，IMF5与负荷的相关性为0.21。经模态组合后，3个模态构成的随机分量与负荷的相关性为0.43，均大于单独的3个模态，证明了本方法的有效性。

3.3 基于模态组合的PSO-LSSVM短期负荷预测

为了说明本文所提基于模态组合的负荷预测方法的有效性，本文分别选用美国新英格兰地区2016年1-2月冬季以及2016年7-8月夏季的工作日负荷、日前电价、温度、湿度数据为数据源进行算例分析。分别建立基于 PSO-LSSVM的原始预测模型、单一预测模型和组合预测模型。原始预测模型，将历史负荷数据和影响因素数据作为 PSO-LSSVM模型的输入，得到预测日的负荷预测值。单一预测模型，将通过 VMD分解及主成分分析法降维处理后的各影响因素的趋势分量、波动分量和随机分量作为 PSO-LSSVM模型的输入，得到预测日的负荷预测值。组合预测模型，采用PSO-LSSVM模型分别对负荷的趋势模态、波动模态、随机模态进行预测，对应的输入为历史负荷及其影响因素对应的模态分量，最后将各模态的预测值累加得到得到预测日的负荷数据。

图7、图8为冬季、夏季3种预测模型预测结果与实际值的对比。表8为预测精度对比。

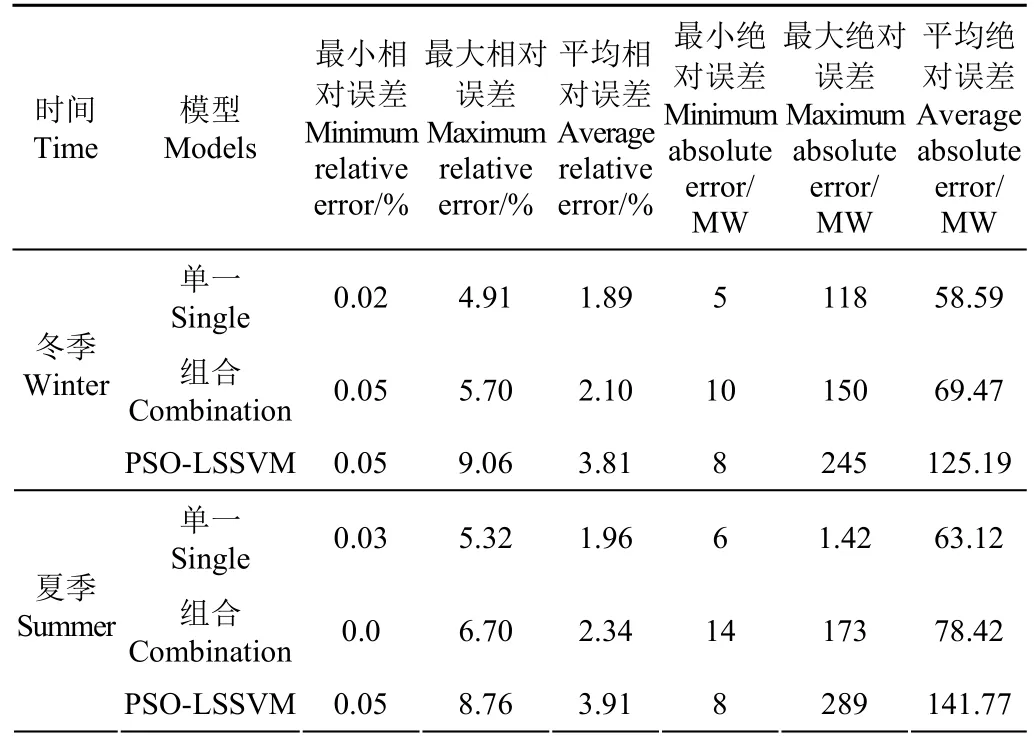
表8 不同模型的日负荷预测精度对比Table 8 Comparison of forecasting accuracy between single model, combined model and original model

从表8中可以看出，除最小绝对误差组合模型最高外，单一预测模型与组合预测模型在各精度指标上，都优于不进行模态组合的原始预测模型。组合预测模型相比于原始模型，最大相对误差降低了3.36个百分点，平均相对误差降低了1.71个百分点，最大绝对误差降低了95 MW，平均绝对误差降低了55.72 MW，证明了模态组合方法在负荷预测工作中的有效性。在本算例中，2种基于模态组合的预测模型均具有良好的预测精度。

针对本算例结果可知，单一预测模型和组合预测模型的的预测精度指标优于原始模型，但 2种模型的优越性比较还需要再进行更加广泛的试验验证。但是组合模型存在的固有误差累计现象不容忽视，这种组合预测模型中出现的固有误差的累计，将严重影响预测精度，可能导致其无法满足短期负荷预测对精度的要求。建议针对不同的数据集分别建立组合预测模型和单一预测模型，选取适合此数据集的精度较高的模型。

4 结 论

本文提出了一种基于模态组合的短期负荷预测方法，本文首先从建立信号分解的评价指标入手，针对负荷预测领域的信号分解特点，制定了包括真实性检验、独立性指标和有效性指标 3部分的评价指标，为信号分解技术的优化方向提供了参考依据。继而利用粒子群优化算法优化变分模态分解的参数，提出了改进的变分模态分解方法。将改进变分模态分解方法分解出的高质量模态进行组合，进行负荷结构辨识以及影响因素拓展。最后，建立了基于模态组合的 PSO-LSSVM 短期负荷预测模型。结合美国新英格兰地区2016年的实测负荷数据进行算例分析，结果表明：

1）本文所提改进变分模态分解方法在信号分解的真实性、独立性、有效性方面均具有显著优越性，可以提供高质量的模态数据序列；

2）本文所提基于模态组合的PSO-LSSVM短期负荷预测方法在高质量影响因素变量的挖掘中能够在数据集不变的基础上显著提升数据利用效率。同时证明了基于模态组合的 PSO-LSSVM 算法相比于直接采用PSO-LSSVM方法，最大相对误差降低了3.36个百分点，平均相对误差降低了1.71个百分点，最大绝对误差降低了95 MW，平均绝对误差降低了55.72 MW。

本文提出的基于模态组合的短期负荷预测方法提高了负荷预测精度，对电力系统调度和电力市场交易起到积极作用。未来可在本文研究结果的基础上，将研究对象扩展至高比例可再生能源电力系统下的广义负荷，深入分析广义负荷的时频特征，完善广义负荷的解析方法；挖掘广义负荷与电价、气象等影响因素在时域、频域的动态关联关系，分析广义负荷对于电价、气象的响应特性，研究考虑互动响应的广义负荷预测方法。