区块链应用下的新型区块链布隆过滤器
2021-10-12牛保宁
樊 星,牛保宁
太原理工大学 信息与计算机学院,山西 晋中 030600
随着区块链的广泛使用,其产生的区块数据也在急剧增加。截至2020年5月8日,比特币[1]已经产生629 473个区块,存储容量为257.28 GB,同比分别增加8.9%和22.4%。支持智能合约的区块链应用——以太坊[2]已经产生10 029 304 个区块,数据总容量达到127.06 GB,同比分别增加47.42%和53.88%。与以比特币和以太坊为代表的公有链相比,许可链Hyperledger Fabric[3]由于有参与节点准入限制,其数据冗余度没有公有链的严重,但是,数据量也在随着业务量的增加和参与节点的增加而快速增加。如何提高链上数据查询性能对区块链的推广和应用提出了巨大挑战[4]。
在对区块链数据分析时,经常需要进行数据查找操作。布隆过滤器(bloom filter,BF)[5]是一个高效的集合查询工具,在以哈希运算为主的区块链应用中不可或缺。轻量级节点由于本地没有保存区块数据,需要依赖远程全节点。为了保护轻量级节点的数据隐私[6],提出由轻量级节点自主选择误判率,将布隆过滤器发送给远程节点,远程节点将运算后的布隆过滤器及满足条件的结果一起返回给轻量级节点,从而避免在数据查询过程中隐私泄露。而对于保存完整数据的全节点,在查询存储在本地LevelDB数据库的区块数据时,利用布隆过滤器可以快速过滤不相干的数据,减少不必要的I/O 开销,提高系统读取性能。
可以看出,作为支持区块链上数据查询的基本工具,提高布隆过滤器的性能对于提高链上数据查询、分析性能至关重要。
1 相关工作
综上所述,布隆过滤器本质上是一种巧妙的概率型数据结构,相比于传统的List、Set、Map 等数据结构,它更高效、占用空间更少,广泛应用于区块链数据查询中。然而,构造布隆过滤器需要大量的内存访问和哈希计算,这将成为区块链数据查询的性能瓶颈。迄今为止,提高布隆过滤器性能的研究主要集中在降低内存访问和减少哈希函数计算开销上,并没有特定针对区块链应用的布隆过滤器优化研究。
降低访存开销主要通过限定布隆过滤器的长度和改变哈希函数。OMBF(one-memory bloom filter)[7]和Bloom-1[8]将元素的映射位限制在一个缓存行内,保证一个元素映射的k位能在一个缓存行中完成读取。OMASS(one memory access set separation)[9]通过将k次哈希函数变换为更复杂的运算,减少在字选择阶段造成的额外的访存次数。它们的共同问题是:访存开销的减少是以增加哈希函数计算复杂度为代价的。
减少哈希函数计算开销主要是通过共享哈希函数计算。LHBF(less Hashing bloom filter)[10]利用两个伪随机哈希函数h1(x)和h2(x)作为种子函数,根据构造公式gi=h1(x)+ih2(x)生成多个哈希函数。另一种思路是:利用O(lgk)个种子函数产生k个相互独立的哈希函数[11]。然而,这些方案缺乏对合成哈希函数间独立性的理论分析,且并未针对区块链数据的特性进行优化,还存在提升的空间。此外,在对布隆过滤器位向量分段情况下,Bloom-1[8]、Parallel BF[12]通过同时访问多个组实现并行计算。然而,这类并行优化只适用于顺序查找,并且多核CPU 固有的并行性使得程序需要进行重写,可行性差。
总之,现有的布隆过滤器并没有充分利用区块链数据特性及通用设备计算资源,存在很大的优化空间。在现有研究的基础上,本文提出一种新的适用于区块链应用的布隆过滤器,即区块链布隆过滤器(blockchain bloom filter,BBF)。与原始布隆过滤器相比,它的内存访问次数和哈希计算开销更低。在此基础上,利用SIMD(single instruction multiple data)指令来对布隆过滤器的构造和查询过程进行并行化,进一步提高BBF 元素查找性能。
2 BBF 设计与理论分析
本章讨论了BBF 的实现方法,并分析了它的假阳性概率。BBF 设计的最终目标是提供一种新的适合区块链数据特性的布隆过滤器。
2.1 新型BBF 架构
布隆过滤器由一个n比特的位数组S={x0x1…xn-1}和k个彼此独立的哈希函数{h1,h2,…,hk}组成,位数组初始化为0。插入元素xs时,将元素xs通过k个哈希函数产生对应的k个哈希值,以哈希值作为位数组中的下标,将k个对应位置“1”。在查询过程中,将该元素通过k个哈希函数映射到对应的比特位,如果存在映射位为“0”,则说明该元素一定不在集合内。
通过布隆过滤器的预过滤操作,可以提高数据的查找效率,然而,传统的布隆过滤器在一次数据查询过程中可能存在多次访存失败的情况。这是因为在区块链应用中,数以亿计的数据信息和有限的内存资源使得布隆过滤器需要选择片外存储方式。而区块链数据以文件形式存储,一个布隆过滤器中往往对应数以万计的元素,相应的,其包含的位数增多,只能连续存储在多个缓存行(cache-line)上。那么在最坏情况下,进行一次区块(交易)查询就会造成k次访存缺失,这对于查询性能的影响是致命的。
为了降低布隆过滤器计算中产生的访存缺失,本文提出一种具有新型布隆过滤器数据结构的BBF。如图1 所示,BBF 由r个连续的长度为lg的组(group)组成,r为2 的幂次方,每个组由k个长度为lw字(word)组成,即lg=k×lw,哈希函数与word一一对应,满足一个word可以被加载到一个通用寄存器的缓存行中,即lw=32(64)bit。一个BBF 有m位,满足关系m=r×lg=r×k×lw。在元素插入及查询过程中,将其映射到一个包含连续的k个word的group中,保证组(group)的长度小于缓存行。
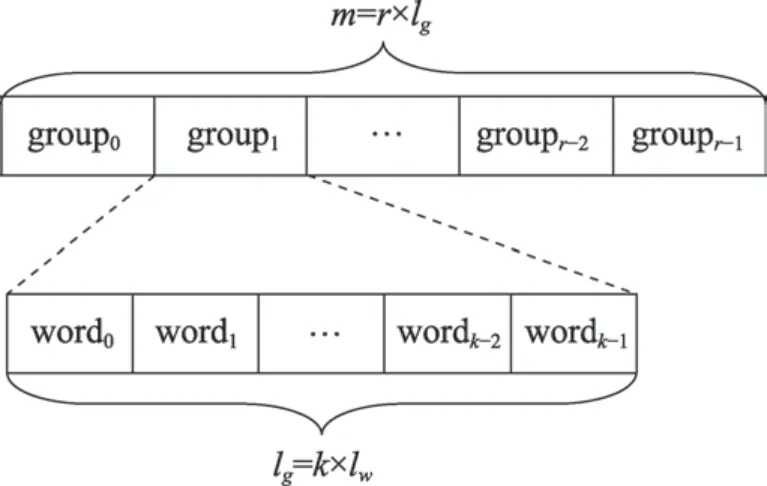
Fig.1 BBF structure图1 BBF 架构
通过改进布隆过滤器结构,一个元素的映射空间限制在一个group中。而一个缓存行可以保存至少一个group,那么在查询过程中,一次访存操作就可以读取到多个group。即使元素映射到的组不在缓存中,也只需要一次访存操作即可读取全部映射位,从而将访存失败次数限制到1 次。为了保证元素与组(group)对应,还需要一个额外的组选择函数。
由于BBF 结构发生改变,可能造成假阳性的变化,为了简化描述过程,下面对BBF 和BF 两者的假阳性进行分析,分别用pBBF和pBF表示。图2 中描述了元素x1的插入过程,哈希函数均选择布隆过滤器中常用的Murmurhash3[13]函数,k=4,lw=4 。对于BF,插入过程可以分为①哈希映射阶段和②取模阶段。而对于BBF,插入过程可以分为①组选择阶段,②哈希运算阶段和③取模阶段。在哈希运算阶段,元素经过k次哈希运算;在取模阶段,将k个哈希值做取模运算,并将对应位置“1”。
根据文献[5]BF 假阳性为:

BBF 通过组映射函数将元素映射到一个选定的组中,然后通过k个哈希函数将组中k个word中的对应位置“1”,其中哈希函数和word一一对应。如图2所示,假定元素x1映射到group1。
BBF 保证元素映射到任意group的概率相等,假阳性事件J表示元素xs不属于集合S,但误判属于S的情况。BBF 中group中任意word未被置“1”的概率为1-1/lw。插入z(z∈[0,n])个元素后,该位仍未被置“1”的概率为(1-1/lw)z,由此可知该位被置1 的概率为1-(1-1/lw)z。用随机变量Z 表示映射到group中的元素个数。则当Z=z时事件J发生的概率为Pr{J|Z=z}=(1-(1-1/lw)z)k。

Fig.2 Schematic view of BF vs.BBF(minimize cache misses)图2 BF vs.BBF(减少访存开销)示意图
Z=z事件发生概率服从二项分布,即Z~B(n,1/r),由此可得:
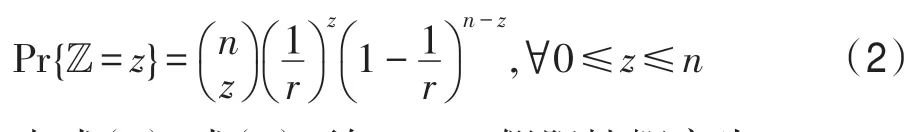
由式(1)、式(2)可知,BBF 假阳性概率为:
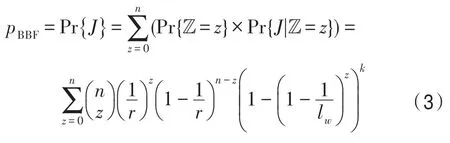
对于给定元素集合,布隆过滤器位数越少,函数碰撞率越高,相应的,假阳性概率也越高。通过式(1)、式(3)无法直观比较两者的假阳性差异,因此对它们的假阳性进行了数值分析,n=104,k=4。定义填充率(fill factor,F)为F=n/m;负载因子L=a/m,其中a为向量中填充为“1”的位数。负载因子表示布隆过滤器中的元素被填充的程度,L越大则布隆过滤器中的元素越多,空间利用率越高。然而,过高的空间利用率可能会导致哈希函数的高碰撞率和高误判率。
哈希表(HashMap)[14]与布隆过滤器类似,都是将当前元素的关键字通过哈希函数映射到数组中的某个位置,当两个不同的元素通过哈希函数得到的存储地址相同时,就会产生哈希碰撞。为了减少哈希函数的碰撞概率,当哈希表的数组长度达到一个临界值就会触发扩容,此时需要将所有元素重新进行哈希运算再放回到容器中,这是一个非常耗时的操作。可以看出,临界值的选择尤为重要,而这个临界值由负载因子和当前的容量大小共同决定。在理想情况下,节点出现的频率在哈希桶中的概率服从泊松分布,实验表明选择0.75 作为负载因子是哈希表对于空间和时间成本的一种折中。考虑到BBF构建过程中存在哈希冲突,存在a≤k×n,因此L=a/m≤(k×n)/m。
从图3(a)可以看出,随着填充率F增加,BF和BBF(lw=32,64)假阳性概率变化趋势一致。当F∈[0.80,1.00]时,变化曲线趋于平缓。图3(b)为F∈[0.02,0.20]时的pBF和pBBF变化情况。图3(b)右(次)纵坐标轴为BBF 与BF 的假阳性概率相对差异,定义为D=(pBBF-pBF)/pBF。当F较小时,BBF 与BF 的假阳性差值变化较大。随着填充率的增加,两者之间的差异越来越小。当lw从32 bit 增加到64 bit 时,两者的差异D几乎减半。当F从0.02 增加到0.20 时,pBF和pBBF(lw=32) 的假阳性概率相对差异从2.98 降低到0.10。类似地,pBF和pBBF(lw=64)之间的假阳性概率相对差异从1.28 减少到0.05。综上所述,可以得出结论:在相同的假阳性概率下,BBF 比BF 需要更多的比特位,这是因为元素的映射位被限制在一个范围内,所以哈希函数碰撞率随之增加。因此,从降低BBF 假阳性概率的角度来看,lw应该尽可能长。然而,实际情况中lw受到缓存行的限制。

Fig.3 False positive ratio of BF and BBF(lw=32,64)图3 BF 及BBF(lw=32,64)假阳性概率
虽然与BF 相比,BBF 假阳性概率更高,但可以通过增加更多的映射位来弥补这一缺陷。实验发现,当pBF=pBBF(lw=32)=0.015 6 时,BF 和BBF 分别需要86 650 bit和100 000 bit。而当pBF=pBBF(lw=64)=0.013 7时,BF 和BBF 需要89 299 和100 000 bit。换句话说,为了保持与BF 相同的假阳性率,BBF(lw=32)和BBF(lw=64)分别需要比BF 多出15.40%和11.98%的映射位。考虑到布隆过滤器的空间效率特性,与区块链的数据量相比,它额外需要的比特位数可以忽略不计,因此该方案是可行的。
2.2 哈希计算优化
通过改变布隆过滤器的映射结构,虽然能够节省访存开销次数,但是需要增加一次组选择哈希函数计算,将元素映射到指定的group中,产生了额外的计算开销,因此本节对BBF 中涉及的哈希计算进行优化。
布隆过滤器中的计算开销主要来自两方面:元素插入时哈希函数的计算和成员查询的哈希计算过程。根据区块链数据的特性,区块(交易)哈希值是对原始数据经过哈希函数运算(SHA256)的结果,是区块(交易)的唯一标识符。而区块链与布隆过滤器选取哈希函数的原则一致,都是要保证函数的随机性、不可逆、低碰撞。传统布隆过滤器采用Murmurhash3函数而不是SHA256 的原因主要是考虑到布隆过滤器需要频繁的哈希运算,虽然SHA256 能够满足以上三个特性,但由于其计算量大,因此没有作为布隆过滤器中的通用哈希函数。而区块链数据特性决定区块链中的数据都是由SHA256 标识,因此,本文提出将SHA256 视为种子函数,利用区块链中的哈希值派生出k个哈希候选值而不是设计多个哈希函数,从而简化哈希计算。
在设计使用一个哈希函数执行布隆过滤器的研究中,如何使用一个哈希函数模拟出k个哈希函数并证明这k个哈希函数相互独立是一个研究难点。而目前的文献研究局限于使用一定数量的种子哈希函数去模拟出k个哈希函数的方法,并没有从理论上证明模拟出来的哈希函数是相互独立的[10,15]。布隆过滤器假阳性概率的分析过程都假设使用的k个哈希函数完全随机,并且相互独立。虽然这些方法有效降低了哈希计算量,但由于缺少哈希函数独立性证明,使得这些方法不能保证布隆过滤器的实际假阳性概率与理论分析值一致。
本文提出的BBF 通过利用区块链数据特性,可以将其视为单哈希布隆过滤器。为了消除对于单哈希布隆过滤器相比传统布隆过滤器可能造成假阳性概率升高的顾虑,进一步论证如下:
BBF 与BF 的实际假阳性概率差异可能并不如理论中那样明显。这是因为实际中用到的哈希函数并非是理想状况下完全随机的哈希函数。所有关于布隆过滤器的理论分析都是基于以下两个关于哈希函数的假设:(1)完全随机。布隆过滤器中使用的所有哈希函数是完全随机的,哈希函数可以将所有的数据元素均匀地映射到整个布隆过滤器范围内。(2)相互独立。布隆过滤器中使用的所有哈希函数相互之间是独立的。
然而,文献[16]中测试了一些实际应用中具有代表性的哈希函数的随机性和独立性,结果显示实际中的哈希函数并不能达到理想状态下完全随机,特别是将哈希函数进行组合之后发现,当哈希函数组合中存在未能通过独立性测试的哈希函数时,相应的哈希函数组合就无法通过随机性测试。也就是说,哈希函数之间存在某种弱相关性。这种弱相关性会导致BF 中的多哈希函数组合假阳性概率跟理论假阳性概率相差很大。
因此在应用布隆过滤器时,哈希函数的选择是非常困难的,尤其是对于比较大的k值。一个差的哈希函数组合选择会导致实际假阳性概率跟理论假阳性概率差值很大[17]。对于一个随机性好的哈希函数,尽管初始化种子不同会展现出比较好的独立特性,但哈希函数的计算仍然会导致计算开销成倍增加。相反,在单哈希布隆过滤器中,它只需要一个随机性好的种子哈希函数。实际中需要的哈希函数越少,就越容易做出正确的选择。另外,如果哈希函数间的相关性被消除,实际的假阳性概率会更接近于理论值。可以将BBF 视为一种单哈希布隆过滤器,选取满足哈希函数随机性和独立性测试的SHA256 作为种子函数。
在组选择阶段,可以将组选择哈希函数简化为一次取模运算j=xsmodr,j为BBF 中映射到的组号。元素映射到任意组后,将元素根据式(4)映射为k个候选元素,与word一一对应,lk为原始位数。
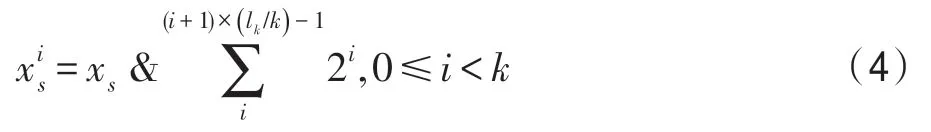
严格来说,BBF 的哈希映射过程仍然有k个相互独立的哈希函数参与,相应地,一个元素对应产生k个映射位。不同之处在于,这k个哈希函数是由k个按位与运算(and)产生的。此外,当m为2 的幂次方时,根据计算机指令集[18]可知,按位与运算与取模运算(modulo)等价,而后者的计算复杂度较前者高,因此可以通过限定m的取值,将取模运算替换为按位与运算(and),进一步提高计算效率。

Fig.4 Schematic view of BBF(cache efficiency optimization)vs.BBF(cache efficiency and Hash computation optimization)图4 BBF(访存优化)vs.BBF(访存及哈希计算优化)示意图
至此,BBF 的构建(查询)过程可以细分为①组选择阶段,②哈希运算阶段和③位运算阶段。元素xs首先被映射到groupj,然后经过k次按位与运算后得到候选集。最后将候选集的k个元素分别映射到groupj的k个word中,并将对应位置“1”。BBF 构建过程为:
步骤1j=xs&(2r-1),将元素xs映射到groupj;
步骤2将元素xs按照式(4)分为k段;
步骤3将候选集中的k个元素映射到对应的word中,映射规则为,并将对应位置“1”。
图4 显示了BBF(2.1 节中提到的访存优化)和BBF(访存及哈希计算优化)示意图。与前一种方法相比,后一种方法不仅消除了哈希函数运算过程,而且将取模操作改为低复杂度的位与运算,完成一个元素插入只需要2k+1 次位与运算,运算复杂度大大降低。
为了定量分析哈希优化的优势,下面以CPU(central processing unit)时钟周期为度量方式,对BF和BBF 在执行元素插入过程中的操作成本进行比较,其中k=4,lk=32 B。时钟周期是计算机中最基本的、最小的时间单位,它刻画了同步动态随机存取内存(synchronous dynamic random-access memory,SDRAM)所能运行的最高频率,时钟周期越低,则意味着工作频率越高。在一个时钟周期内,CPU 仅完成一个最基本的动作。
在CPU 指令中,通常情况下,按位运算需要3 个CPU 时钟周期。在实验服务器上进行性能测试表明,一次取模运算平均需要6 个CPU 时钟周期;选用Murmurhash3 作为哈希函数,每个字节平均需要23个CPU 时钟周期。由表1 可知,对于一次元素插入操作,BBF 需要192 个时钟周期,约为BF 计算量的5%。BBF 的性能较BF 有显著提升,这是因为BBF 的哈希计算量大大降低了。此外,由于普通哈希函数的计算时间成本随着元素长度的增加而增加,观察到随着元素大小和哈希函数数目的增加,BBF 较BF 性能优势明显。这一点在3.2节的实验中也得到了验证。
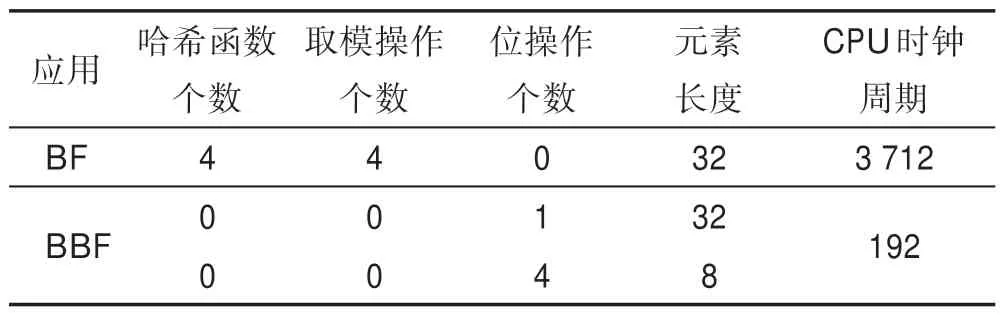
Table 1 CPU clock cycles comparison on element insertion between BF and BBF表1 BF 及BBF 元素插入所需CPU 时钟周期
2.3 利用通用CPU 的SIMD 指令集优化BBF
为了加快BBF 中元素插入和查询效率,通过改变布隆过滤器结构减少了访存失败的次数和哈希计算开销。在成员查询过程中,需要依序检查元素对应的k个映射位。如果所有的k位都设置为1,那么这个元素可能包含在集合中。考虑到元素在插入和查询过程中k个候选元素彼此独立,不存在相关性。如果能将它们并行化,就有可能进一步改进BBF。计算机硬件的进步对软件的编写方式产生了巨大的影响,SIMD指令集[19]可以实现同时对p对数据流执行算术运算,即(c1,c2,…,cp)=(a1,a2,…,ap)+(b1,b2,…,bp)。
然而,BF 与SIMD 指令集并不适配,这是因为在布隆过滤器的查询过程中,元素的映射位存在于整个布隆过滤器中,而SIMD 指令集可以同时处理加载到的连续位向量,提高数据处理效率。但是由于SIMD 一次读入的数据有限,对于传统的布隆过滤器,无法一次访问全部映射位,从而无法充分利用SIMD 指令集的优势。而BBF 对BF 结构的改变正好与SIMD 的特性相吻合,支持一次读取k个待查询比特位的并行处理。基于BBF 的结构特性和运行机制,SIMD 指令主要应用在BBF 构建和元素查询两方面,提高元素插入/查询效率。在元素插入过程中显式调用SIMD 指令,伪代码见算法1。
算法1BBF 构建算法
输入:xs区块链交易哈希值。
输出:BBFo1。

相应地,BBF在元素查询阶段的伪代码见算法2。
算法2BBF 元素查询算法
输入:xs,BBFs(BBF 候选集合)。
输出:BBFt目标BBF。

3 实验与结果分析
为了优化区块链应用中的布隆过滤器,本文提出三个改进措施。本章对BBF 性能进行了实验。
3.1 实验设置
实验环境为Intel®CoreTMi7-8700K CPU@3.70 GHz,32 GB内存。每个核心有独立的一级缓存(L1 D-Cache 32 KB,L1 I-Cache 32 KB)和二级缓存(256 KB)。6个核心共享三级缓存(12 MB),缓存行为64 B。实验使用AVX2 指令集,支持256 bit 整数算术运算。Gcc编译器支持AVX2 指令的程序设计。
实验选用存储在LevelDB 数据库中的比特币数据集,lk=256。数据集1 为交易索引,表示为<‘t’+32-byte transaction hash,transaction index record>,共50 000 000 项;数据集2 为区块索引,描述为<‘b’+32-byte block hash,block index record>,共50 000 项。在元素查询性能实验中,正向查询是指查找属于集合的元素,负向查询是指查找不属于集合中的元素。布隆过滤器的位数组是缓存行对齐的,使用每秒百万次搜索(MSPS)作为查询速度评价指标。实验采用BF[5]和OMBF[7]作为对比方法。BF 为标准布隆过滤器,OMBF 是一种最先进的布隆过滤器方法,它通过减少缓存丢失来提高成员查询性能。
3.2 性能评价
(1)假阳性概率。实验选取pBBF(lw=64)在两个数据集上分别进行实验。如图5 所示,不同数据集上的实验结果与2.1 节中的理论分析变化趋势一致,实验结果基本吻合,可以得出BBF 成员查询方法具有良好的随机性,参数设置符合预期,验证了2.1 节中对于BBF 的假阳性概率分析。同时,为后续实验中填充率的选择设置起到指导作用。

Fig.5 False positive ratio comparison between theory and measured results of BBF图5 BBF 假阳性概率理论值与测试值分析
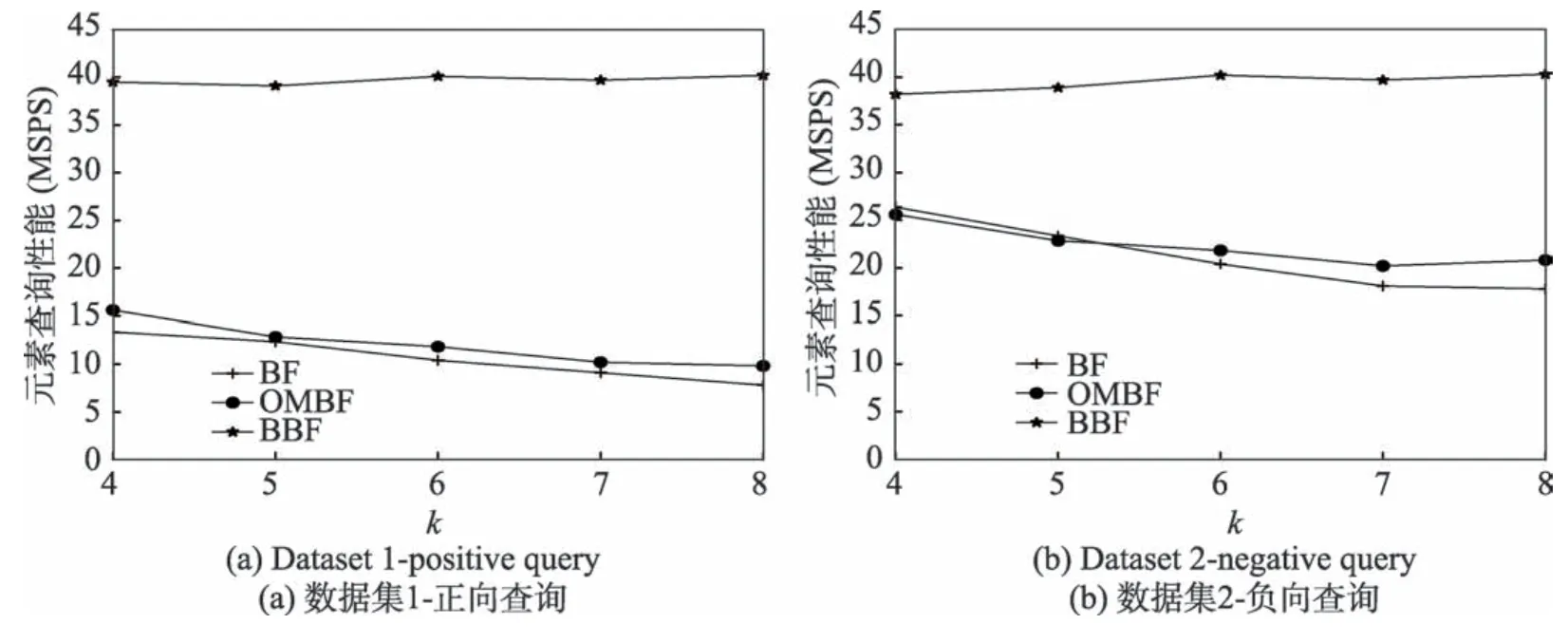
Fig.6 k vs.membership query performance图6 k vs.元素查询性能
(2)搜索代价。最小化缓存缺失和减少哈希操作有助于降低成员插入和搜索代价。而SIMD 指令又进一步提高了BBF的查找性能。图6为在不同数据集上布隆过滤器查找性能对比,n=105,m=106,F=0.1。
理论上来说,正向查询相比负向查询需要检查更多的映射位,因此哈希运算数也会增加,对于BF 和OMBF,图6(a)中的正向查询相比图6(b)中的负向查询性能有所降低。随着哈希函数个数k的增加,BF 和OMBF 查询速度呈下降趋势。这主要是因为BF 和OMBF 在查询过程中使用串行位检测。随着k的增加,待检测比特位也随之增加,因此速度下降。而BBF 采取并行的位检测方法,显示出近似恒定的查询速度。
OMBF 的性能优势在于降低成员查询过程中的内存访问开销,在本实验环境中,CPU 有足够的缓存(32 GB),因此OMBF 的成员查询速度较BF 相比,查询性能优势并不明显。从图中可以看出,当k=8 时,在正向查询中,BBF 的成员查询速度分别为BF 和OMBF 的4 倍、3 倍;在负向查询中,BBF 的成员查询速度是其他两类布隆过滤器的2 倍,BBF 较其他两类具有代表性的布隆过滤器BF 和OMBF,查询性能更优。
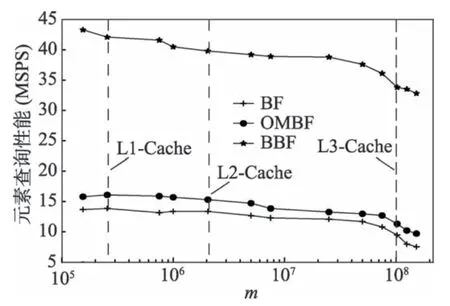
Fig.7 m vs.membership query performance of BF图7 m vs.布隆过滤器元素查询性能
图7 为布隆过滤器位数m与布隆过滤器查找性能的变化关系图,为了表明缓存与查找性能之间的关系,将L1、L2 和L3 三级缓存在图中做了标识。当CPU 缓冲区足够大时(m
4 结论
本文提出了一种针对区块链应用的新型布隆过滤器BBF。通过改进布隆过滤器数据结构减少访存缺失次数,同时提出一种简化的三阶段哈希运算。在此基础上,运用SIMD 指令实现元素插入及查找并行化。实验结果表明,BBF 仅需要11.98%额外的映射位,就能在假阳性概率不变的同时,较其他两种广泛应用的布隆过滤器性能有显著提升。
