热扰动冲击下的高温超导电缆失超恢复特性
2021-10-11祝乘风厉彦忠谭宏博史佳敏
祝乘风 厉彦忠 谭宏博 史佳敏 聂 杨
(西安交通大学能源与动力工程学院 西安 710049)
0 引言
随着高温超导(High Temperature Supercondu- cting, HTS)材料的不断发展,高温超导技术在储能和输电系统中得到广泛的研究和应用[1-4]。高温超导输电系统因其低功耗、高能量输送效率[5-6]、大容量和布局紧凑等优点,有望成为一种高效的能源传输系统。厉彦忠等[7]提出了一种新型的长距离能源输送系统,该系统将液化天然气(Liquefied Natural Gas, LNG)输送与超导电缆的电力传输相结合:超导电缆浸没在LNG中,由过冷LNG为超导电缆提供低温环境,可降低LNG输送和超导电缆的冷却和运行成本。由于LNG易燃易爆,在LNG和超导电缆之间需要添加保护介质(液氮)。LNG作为冷源在外管中流动,而液氮填充在内管中[8-9]。
高温超导电缆在正常工作中,难免会遇到各种各样的热扰动冲击,例如,洛伦兹力引起的机械扰动、磁通跳跃、局部漏热等。这些冲击达到一定强度后会造成超导电缆的局部失超,进而沿着电缆传播,引起整体失超,严重时会造成电缆烧毁[10-11]。因此,对电缆失超传播特性的研究具有重要意义。实验表明[12],电缆铜骨架的结构可以有效地抑制直流冲击下焦耳热的生成,一定条件下高温超导电缆在直流冲击下失超是可以自行恢复的。诸嘉慧等[13-14]在等效电路模型的基础上,建立了零维的传热模型,通过时间离散方法,对超导电缆进行了磁热耦合计算,得到了在故障电流作用下的电流分布特性。结果表明,冷绝缘高温超导电缆的铜骨架分流作用明显,能承载96%的故障电流。本文在此基础上,建立一维的传热模型,考虑不同液氮流速下,探究热扰动冲击下电缆失超及其恢复特性。
1 高温超导电缆模型
冷绝缘高温超导电缆系统结构示意图如图1所示,其中电缆本体与液氮直接接触,过冷液氮在环形通道内强制流动,为电缆本体提供低温的工作环境,使超导带材处于正常工作的超导态。考虑到LNG/电力混输的应用前景,本文研究高温超导电缆在80K工作温度下的运行特性。电缆本体由内至外分别为铜骨架、碳纸层、超导层、电绝缘层、屏蔽层。其中超导层由m根钇钡铜氧(YBa−Cu−O−, YBCO)超导带材组成,螺旋缠绕在碳纸上。本文取m=60。电缆本体的正常工作电流为3kA,故每根超导带材上所承载电流为50A。电缆本体外直径为10mm,液氮管内直径为30mm,电缆长度为1m,液氮入口温度为80K,为保证液氮处于过冷状态,液氮被加压至1.0MPa,流速为0.1m/s。

图1 高温超导电缆系统结构示意图 Fig.1 Schematic of HTS cable system
2 数值仿真模型
数值仿真模型包含两个子模型,即超导电缆等效电路模型和超导电缆传热模型。本文通过电热耦合算法,实现等效电路模型和传热模型的耦合计算,从而求解高温超导电缆失超和恢复过程中电磁场和温度场之间的复杂耦合特性。
2.1 超导电缆等效电路模型
为了计算电流在超导带材和铜骨架之间的分布情况,本文在前人研究成果[13-15]的基础上建立了等效电路模型,如图2所示,该模型普遍用于电缆电流分布计算。该模型将超导层的各根超导带材并联,再与铜骨架并联。在局部失超的时候,失超点处会首先出现电流分流现象,即由于电缆本体温度升高,超导带材临界电流降低,超导电缆进入磁通流阻态。超导带材能承载的电流减少,而多余的电流会由铜骨架承担,并产生焦耳热,使电缆本体温度进一步升高,直至完全失超。

图2 等效电路模型 Fig.2 Equivalent circuit model
当电缆承载直流电流时,该模型可忽略屏蔽层的电流分布,且电流的变化产生的自感和互感对层间电流分布影响可忽略不计。
图2中,Iop为电缆本体流过的正常工作电流,Icond为流经超导层中的电流,If为流经铜骨架中的电流,I1~Im为流经超导带材1~m中的电流;对应地,R1~Rm为各根超导带材的电阻,Rf为铜骨架的电阻。
根据基尔霍夫定律,电缆本体内的电流分布表示为
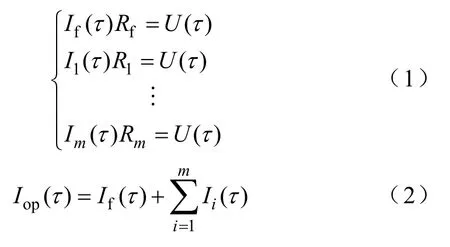
各层超导带材的U-I特性遵循n值幂律关系为

式中,Ui为电压降;Ii为电流;l为带材长度;E0为失超判据,E0=1×10−4V/m;n为品质因数,根据实验数据[16-17],取n=31.9;Ic为YBCO带材的临界电流(一般由实验测得),随温度升高而降低,Ic可表示为

式中,Tc为带材临界温度;Tcs为电流分流起始温度。当电缆温度超过带材临界温度后,带材不再承载电流,故临界电流一直为零。根据实验数据[18-19],电流分流阶段YBCO带材的临界电流值采用线性拟合,即

通过联立方程式(1)~式(5)便可求解出电缆中的电流分布。
2.2 超导电缆传热模型
在热扰动冲击下,电缆局部温度会急剧升高,沿轴向存在显著的温度梯度,因此会发生沿电缆轴向的导热。本文在前人基础[20]上,建立了一维传热模型,其中电缆本体由铜骨架和超导带材构成。电缆本体轴向一维非稳态导热方程为
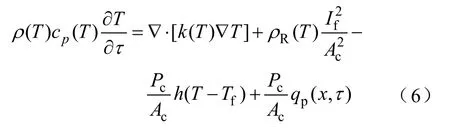
式中,Pc、Ac分别为电缆本体的周长和横截面积;If为流经铜骨架的电流,由等效电路模型计算获得;Tf为冷却介质液氮的温度;ρ、cp、k分别为电缆本体的密度、比热容和导热系数;T为电缆本体的温度;ρR为铜骨架电阻率。方程右边分别为热扩散项、焦耳热源项、冷却源项和热流脉冲源项,分别代表着沿轴向传导的热量、电流在电缆本体上产生的焦耳热、过冷液氮带走的热量和热流脉冲产生的热量。这些物性参数都是温度的函数,在仿真过程中随温度实时变化。
由于本文研究的液氮流动处于湍流区(雷诺数超过5 000)且液氮处于过冷态(饱和温度103K),未发生相变,故液氮强制对流换热系数由Gnielinski公式确定,即

式中,Re为雷诺数,Re=ρlvDl/μ,ρl为液氮密度,μ为液氮动力黏度,v为液氮流速,Dl为当量直径;f为管内的Darcy阻力系数,f=(1.82lgRe− 1.64)−2;Pr为普朗特数;λ为液氮导热系数。
高温超导体在运行中会受到各种外部扰动因素的影响,例如,超导带材受到机械摩擦或磁通跳跃带来的局部热流影响,导致该处带材温度骤然升高,温度超过超导临界温度后会局部失超,并向周围传 播[21-24]。为简化模型,假设在初始时刻,液氮入口端长度lp的区域存在一个局部热流脉冲,一维传热模型及其离散化处理如图3所示。热流脉冲持续时间τp,释放热量为Qp,可表示为

本文取lp=5cm,τp=1s,Qp=500J。
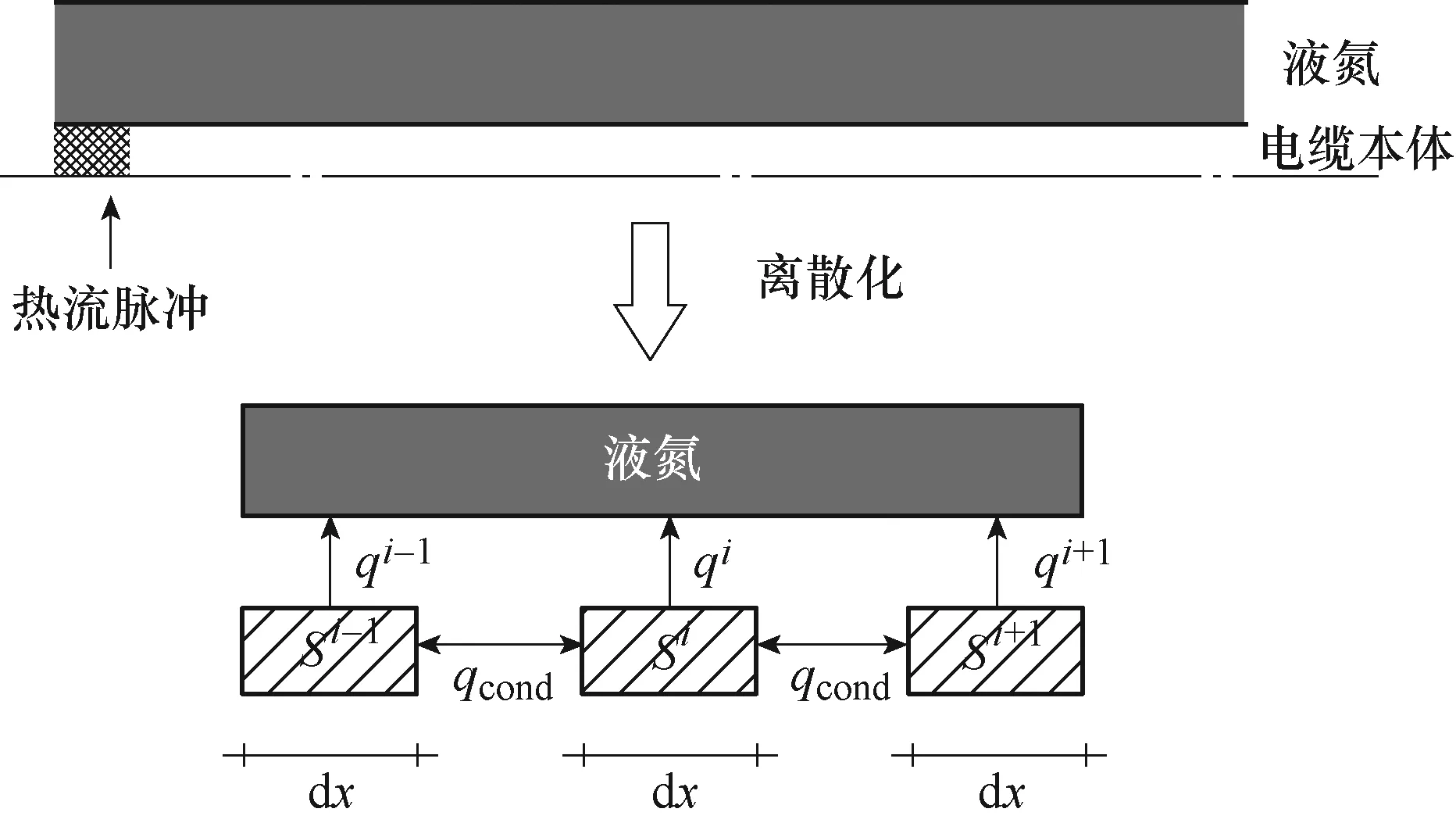
图3 一维传热模型及其离散化处理 Fig.3 A 1-D heat transfer model and its discretization
2.3 电热耦合算法
如图3所示,将电缆本体沿着轴向均匀划分节点,采用有限差分法[25]计算电缆的非稳态导热。其中qcond为沿着电缆轴向的超导热流,dx为节点间距,qi为节点i与液氮之间的换热量,Si为节点i处的热源,包括铜骨架上的焦耳热和外部脉冲热流。
电热耦合算法通过Python程序实现,计算程序流程如图4所示。计算过程中,初始时刻电缆本体处于正常工作温度80K,首先根据温度计算电路参数,代入等效电路模型得到电流分布,将电流代入一维传热模型得到温度分布,再计算下一时间步长的电路参数,如此迭代,实现电场和温度场的耦合求解。

图4 计算程序流程 Fig.4 Calculation flow chart
3 结果与分析
3.1 高温超导电缆失超恢复
当液氮流速为0.1m/s时,不同时刻下电缆本体整体的温度分布如图5所示。τ=1s时,电缆左端5cm段在热脉冲作用下温度达到98.5K,此时左端电缆向右扩散传导的热流大于电缆产生的焦耳热,故温度开始降低,到τ=18s时左端点温度已降至92.1K;到τ=19s时左端点温度已降至91.7K,低于临界温度92K,此时电缆开始出现分流现象,进入磁通流阻态,失超开始恢复,直至电缆完全恢复超导态。

图5 不同时刻下电缆本体整体温度分布 Fig.5 The temperature profile of the cable at different times
电缆本体左端x=0m和x=0.1m处的温度变化如图6所示。从图6可见,电缆左端点温度在热流脉冲和焦耳热的作用下,由初始的80K迅速升高至98.5K,随后热流脉冲撤去,该处温度逐渐降低,直至降低到电缆临界温度92K,此时电缆无焦耳热,故降温速率加快,迅速降至工作温度80K。在整个过程中,电缆的高温区并没有向右端扩散,此时失超仅发生在距左端10cm区域,这得益于液氮的强制对流冷却,使电缆左端经历失超后又逐渐恢复至正常工作温区。与前人文献[20]中结果相比,本文的耦合计算模型更能反映电缆降温速率的变化。
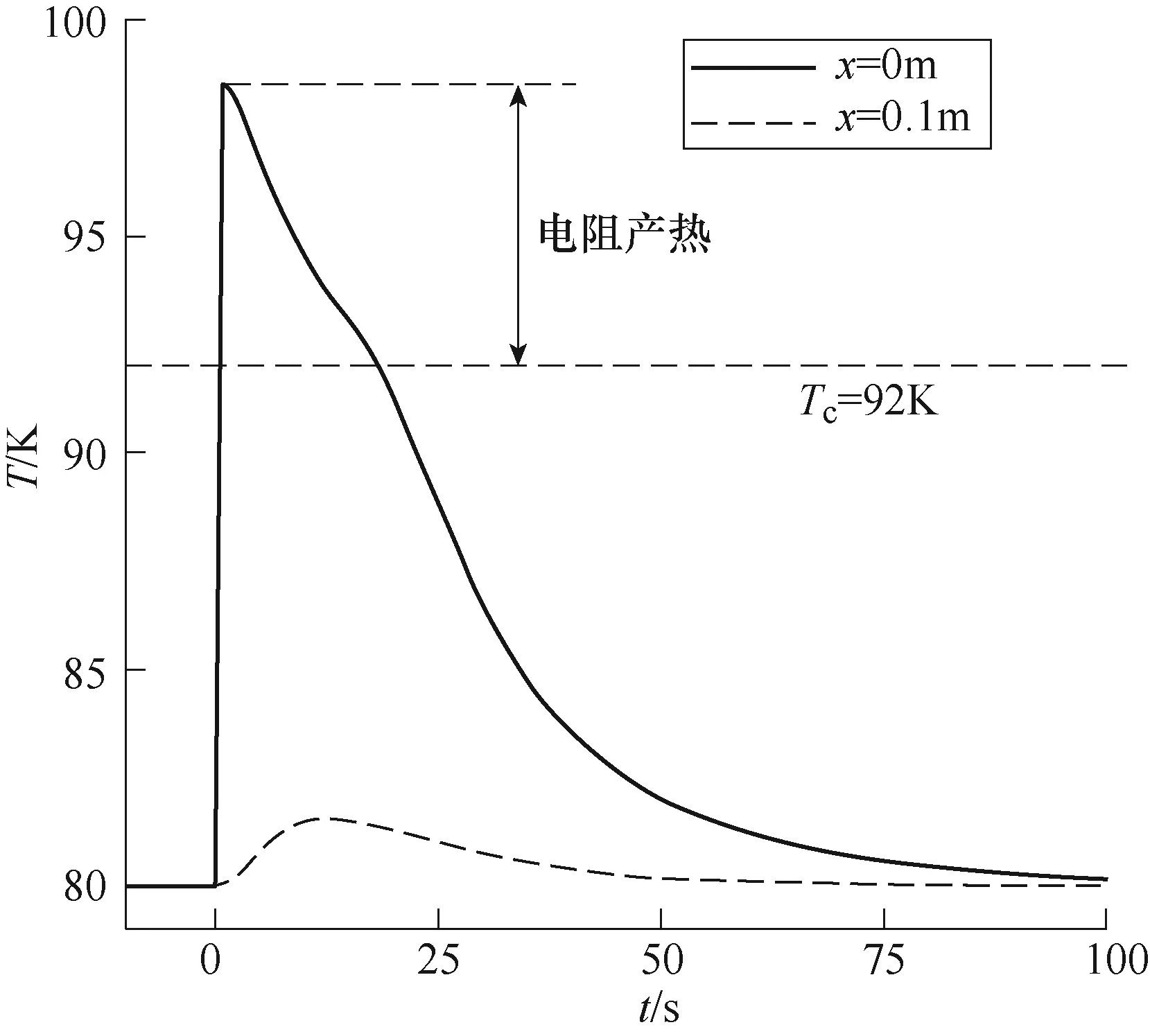
图6 电缆本体左端x=0m和x=0.1m处的温度变化 Fig.6 Temperature varies with time at x=0m and x=0.1m at the heat point of the HTS cable
3.2 热流脉冲对失超恢复的影响
为探究热流脉冲对高温超导电缆失超恢复过程的影响,本文计算了不同热流脉冲能量下电缆左端点温度变化情况,不同脉冲热量下电缆左端温度随时间变化如图7所示(液氮流速0.07m/s)。当脉冲能量小于330J时,电缆左端点最高温度不会超过电缆临界温度92K,故不会失超。当脉冲能量为400J和500J时,电缆左端点温度超过92K,致使电缆左端失超,随后在液氮的强制对流冷却下逐渐恢复。 而当脉冲能量为550J时,液氮的冷却不足以使电缆的失超恢复超导态,失超段会沿着电缆轴向传播。因此,存在两个临界热脉冲能量:临界失超能量和临界恢复能量。
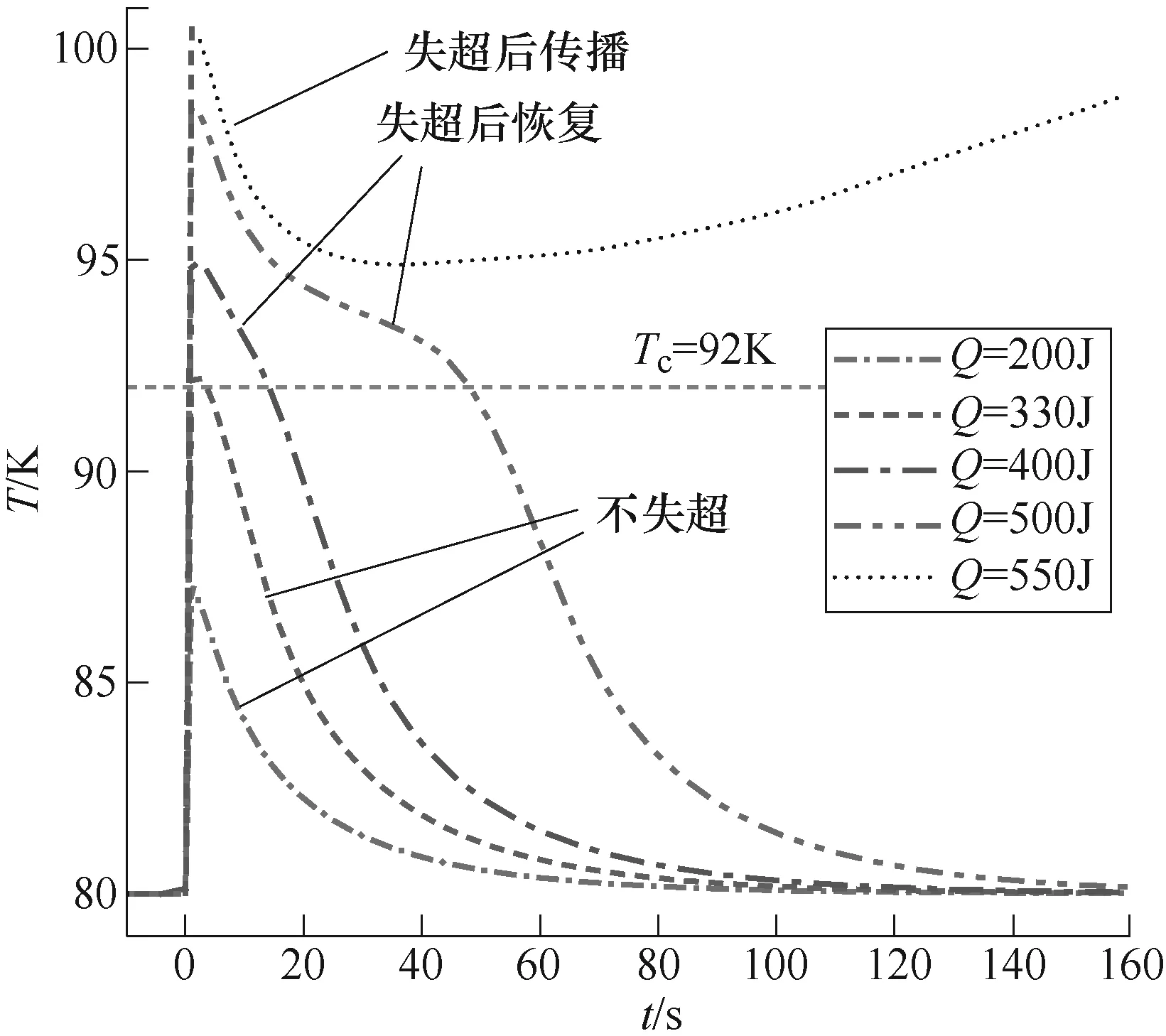
图7 不同脉冲热量下电缆左端温度随时间变化 Fig.7 The temperature at the heat point of the cable varies with time under different heat pulse energy
图8展示了在相同的脉冲能量下脉冲持续时间对电缆左端温度变化的影响(液氮流速0.07m/s)。可见,脉冲持续时间对电缆恢复过程的影响不大。

图8 不同脉冲时间下电缆左端温度随时间变化 Fig.8 The temperature at the heat point of the cable varies with time at different pulse times
3.3 液氮流速对失超恢复的影响
为探究液氮流速对高温超导电缆失超恢复过程的影响,本文计算了不同液氮流速下电缆失超恢复情况。图9展示了不同液氮流速下电缆左端温度随时间的变化情况。图中可见,在不同液氮流速下,电缆左端点在1s时能达到的最高温度都在98.5K左右。当液氮流速大于或等于0.07m/s时,左端点温度能够被冷却到92K以下,即恢复超导态,且液氮流速越大,降温的速率越大。当液氮流速小于或等于 0.06m/s时,电缆左端点温度一直保持在92K以上,且先降低后持续升高,电缆一直处于失超状态,且不断向右传播。

图9 不同液氮流速下电缆左端温度随时间变化 Fig.9 The temperature at the heat point of the cable varies with time at different liquid nitrogen velocity
在不同的换热情况下,电缆临界热脉冲能量在不同努塞尔数下的分布如图10所示。随着努塞尔数的增大,临界失超能量呈线性增大,而临界恢复能量呈指数增大。
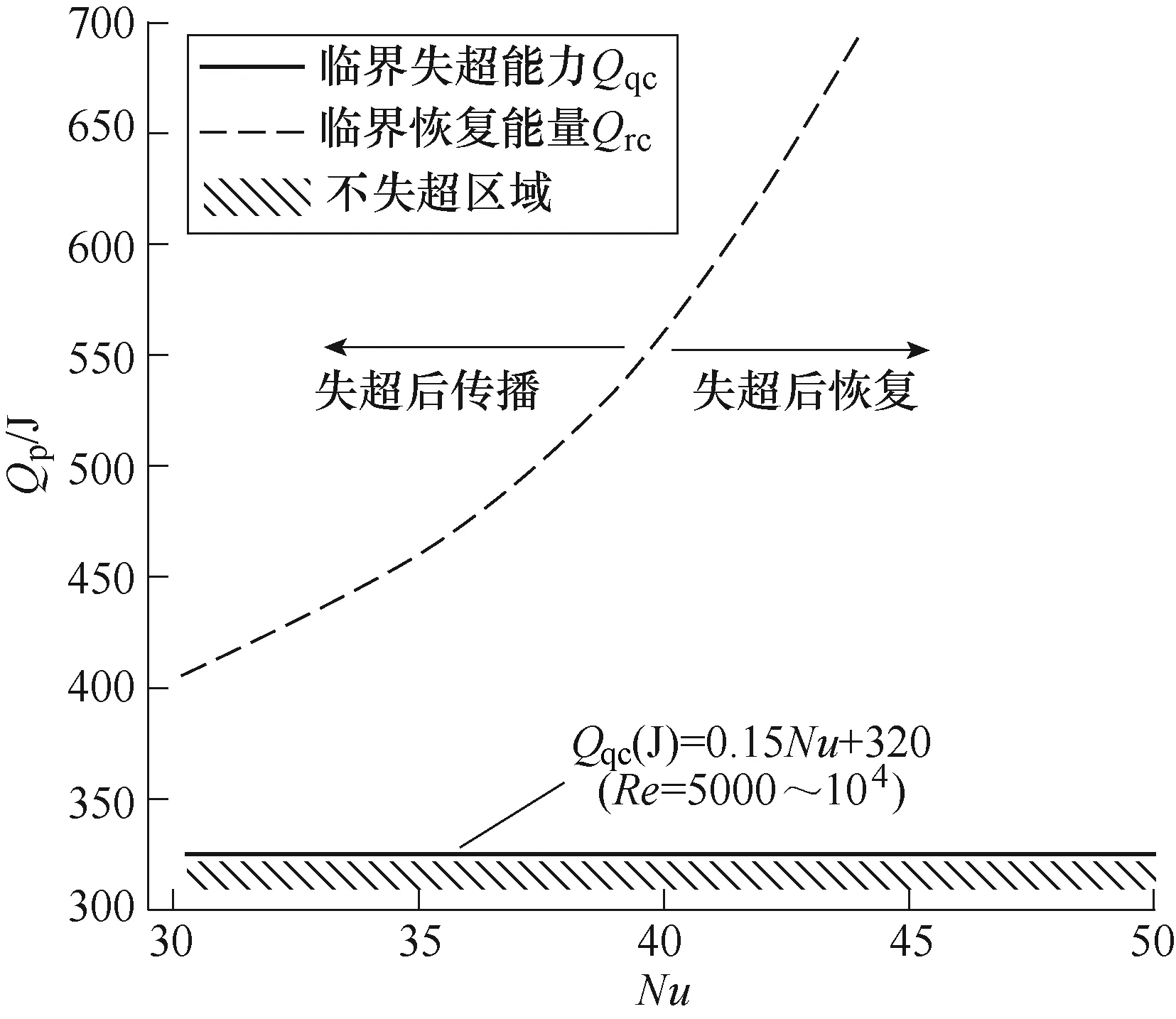
图10 临界失超能量和临界恢复能量随努塞尔数的分布 Fig.10 The critical pulse energy of quench and recovery vary with the Nusselt number
当失超发生后,铜骨架上承载了工作电流,对于恢复过程,当铜骨架上不再承载电流时,电缆的失超被认为是完全恢复,此时的耗时被认为是恢复 时间。图11展示了在不同热流脉冲能量的情况下,液氮流速对恢复时间的影响。热流脉冲能量越大,失超恢复的时间越长。随着液氮流速的增大,超导电缆失超恢复时间不断降低,且呈幂律关系。
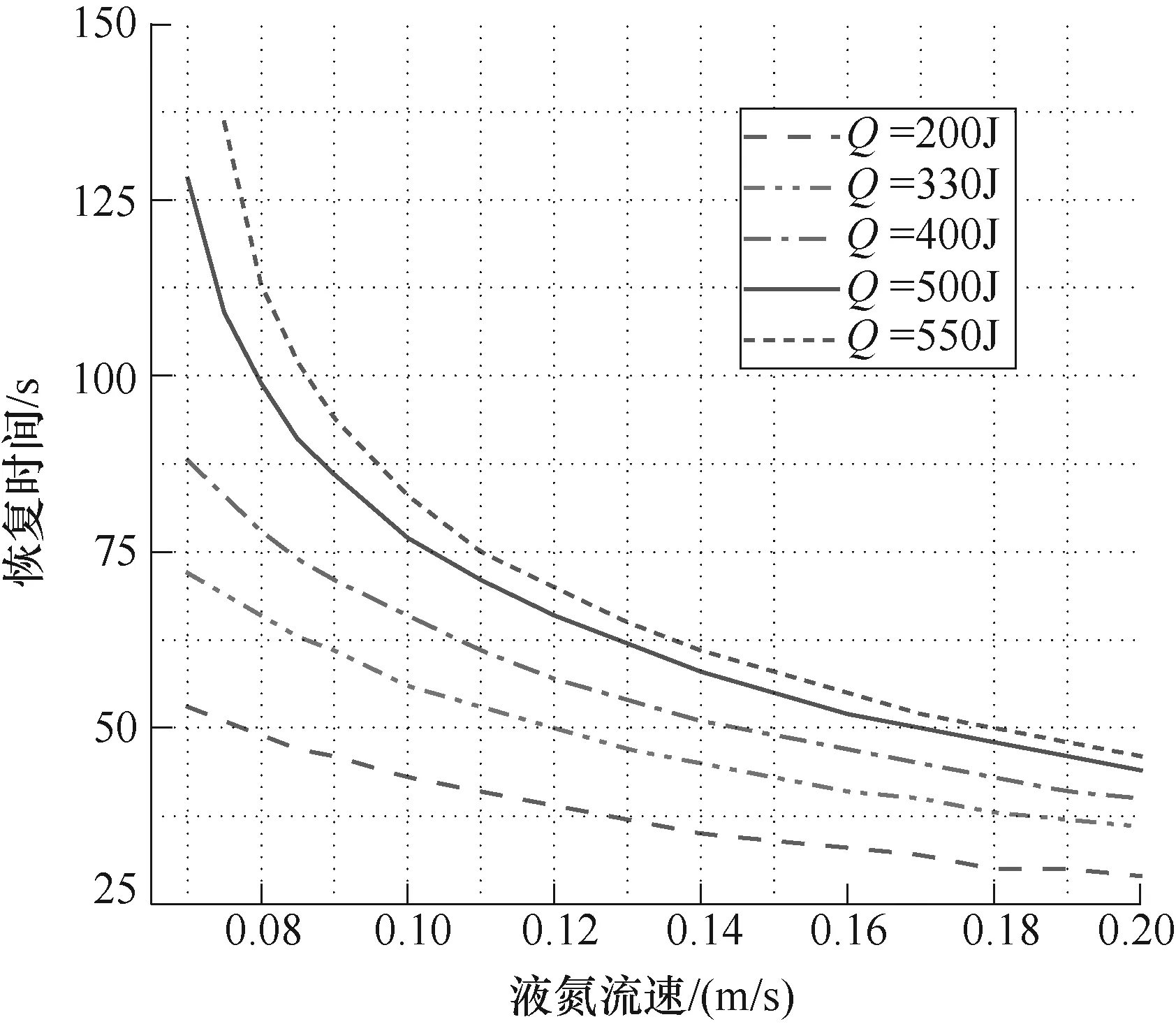
图11 不同热流脉冲下液氮流速对失超恢复时间的影响 Fig.11 The influence of liquid nitrogen velocity on recovery time of quench under different heat pulse energy
4 结论
本文针对外径10mm的高温超导电缆在3kA电流传输时的局部失超传播过程建立了一维仿真模型,模拟了在热扰动冲击下高温超导电缆的失超恢复特性。本研究模型有别于传统的失超模型,通过有限差分法对电缆长度和时间进行离散,可同时实 现电流分布仿真和沿电缆轴向一维导热的耦合模拟,获得高温超导电缆失超过程沿轴向的瞬态分布和演变情况。针对本文研究的超导电缆结构和工况,得到以下结论:
1)本研究中,当热扰动能量小于临界失超能量Qqc时,电缆不会发生失超;当热扰动能量大于Qqc且小于临界恢复能量Qrc时,电缆发生失超,且在液氮冷却下逐渐恢复至超导态;当热扰动能量大于Qrc时,电缆的失超不能被液氮的冷却所抑制,失超段沿轴向传播,导致整体失超。
2)临界失超能量Qqc随努塞尔数的增大呈线性增大,临界恢复能量Qrc随努塞尔数的增大呈指数增大。可通过合理设计低温冷却流体的流动工况,增加强制对流冷却强度,以提高电缆安全运行的热扰动裕度。
3)当热扰动能量低于临界恢复能量时,电缆恢复时间与液氮流速呈幂律关系。故在高温超导电缆结构设计时,应结合电缆管道结构,合理设置液氮流量,以确保超导电缆被充分冷却,使局部失超得到有效抑制。
