不平衡磁悬浮转子自动平衡仿真分析

王丛涛，郭 辉，孙 凤

(沈阳工业大学 机械工程学院,辽宁 沈阳 110870)

0 引言

磁悬浮轴承是一种利用可控磁力将转子悬浮于空中，使定子与转子之间实现无接触支承的一种新型高性能轴承。从产生磁力的方式上划分，磁悬浮轴承可划分为三大类，即主动磁悬浮轴承(Active Magnetic Bearing，AMB)、被动磁悬浮轴承(Passive Magnetic Bearing，PMB)和混合磁悬浮轴承(Hybrid Magnetic Bearing，HMB)[1]。其中，主动磁悬浮轴承是基于闭环反馈控制的典型机电一体化产品，由于主动控制的存在，使得主动磁悬浮轴承具有刚度和阻尼可控、可补偿转子不平衡振动等特点，因此在工业应用中最为广泛，目前其主要应用于透平机械[2]、机械加工[3]、航空航天[4,5]、人工心脏[6,7]、核能发电[8]等领域。

而在旋转机械中，由于材料均匀性、加工误差等原因，再加上高精度的动平衡成本高昂，使得转子存在不平衡量成为普遍现象，不平衡量是引起旋转机械振动的主要原因。由于磁悬浮轴承的支承刚度相对较小，转子的不平衡量随着转速的增加，离心力增大，轴承所产生的电磁力并不能完全约束转子绕其几何对称轴旋转，而是限制转子绕其惯性主轴和其几何主轴之间的某一未知轴线旋转[9]。其中，旋转轴偏离几何轴产生不平衡位移，使系统产生振动位移，导致转子的径向跳动增大；转轴偏离惯性主轴产生不平衡力，使系统产生振动力，从而降低整个系统的稳定性。如何对不平衡振动进行抑制，已经成为主动磁悬浮轴承向更高转速发展的主要障碍。而自动平衡补偿控制便是针对后者的一种主动抑振控制方法。

本文从转子动力学出发，分析得出磁轴承不平衡转子响应表达式，解释了自动平衡补偿控制的实现原理；并基于MATLAB的Simulink工具箱建立了主动磁悬浮轴承系统模型，通过仿真验证了理论计算的正确性。

1 转子不平衡响应分析

本文研究对象为一台五自由度主动磁悬浮轴承实验平台，它由两组径向磁轴承与一组轴向磁轴承构成，分别约束转子的4个径向自由度与1个轴向自由度。如图1所示，首先对转子进行受力分析，在质心处建立空间直角坐标系。由于转子为刚性转子，将径向磁轴承与轴向磁轴承视为无耦合，径向磁轴承对转子施加的两个相互垂直的力相互独立。其中，Fx、Fy分别为左侧磁轴承对转子施加的水平与竖直方向的电磁力，m为转子质量，g为重力加速度，ω为转子角速度。

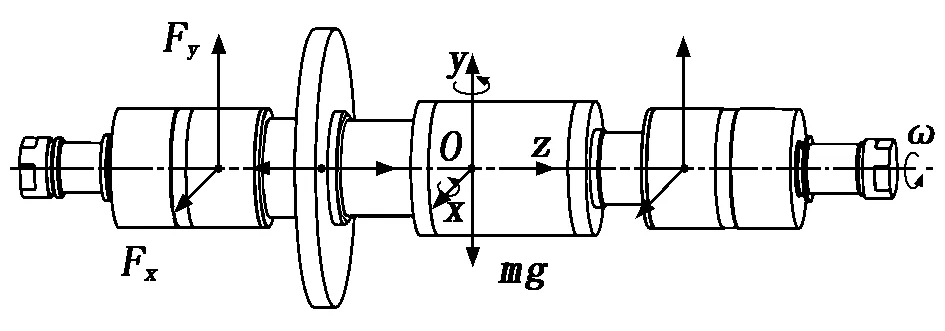
图1 转子受力分析简图

图2为质心截面示意图。由于不平衡量的存在，导致质心Om与几何中心Or不重合。

图2 质心截面示意图

设fx与fy分别为不平衡量所产生的离心力在x、y轴上的分量，大小为：

(1)

其中：e为偏心距；t为时间。当转子以角速度ω旋转时，质心Om的加速度在坐标轴上的投影为:

(2)

其中：x、y分别为几何轴心在x、y轴上的位移分量；xm、ym分别为惯性轴心在x、y轴上的位移分量。在弹性支撑的状态下，有：

(3)

z=Aeiωt.

(4)

(5)

其中：A为振幅。

由式(4)与式(5)可知，几何中心Or的响应频率与不平衡量的激振频率相同，而且相位或相等或相差180°。这说明，点O、Or、Om始终在一条直线上。由于磁轴承的支撑刚度较低，因此通常角速度ω>ωn，A<0，但|A|>e，O点落在Or与Om之间。随着角速度ω的上升，当ω≥ωn时，A≈-e，振动很小，转动反而比较稳定。由于偏心距的存在，导致转子几何中心存在与转速同频的规律性变化，控制器采集含有与转速同频不平衡响应的位移信号，同时输出带有转速同频的电流控制信号，从而约束由于质量偏心产生的扰动。而这也导致不平衡振动通过磁轴承传递至外部壳体，引发外部壳体的振动。同时，由于线圈中存在转速同频的电流，导致功放容易饱和，降低了主动磁悬浮轴承系统的稳定性。

由式(5)可知，A的大小与ωn的大小相关，当ωn足够小时，即刚度k足够小时，转子将绕着质心轴旋转。在上述分析中，为方便分析计算，将磁轴承假想成定刚度的理想弹性支撑。而实际磁轴承的支撑刚度是通过控制器采集位移信号实时计算出的动态刚度，控制器将位移信号与设定的平衡位置进行对比，通过控制算法计算从而得到对应线圈中的电流值，控制功率放大器产生驱动电流，产生电磁力对转子进行约束，因此其刚度主要由控制算法决定。由于不平衡量的存在，导致转子旋转偏离转子的几何中心，当转子围绕其质心轴旋转时仍然存在偏离，这都将导致位移信号中存在转速同频的变化量。如果控制器不对由于不平衡量所产生位移量进行控制，即理解为刚度k≈0 N/m，转子即可实现围绕转子质心轴旋转，并且当|A|→e时，转子轴心轨迹半径减小，转子旋转精度将有所提升。

由上述可知，不平衡响应信号具有与转速同频的特点，同时位移信号中也存在转速同频的变化量，而位移信号的变化则直接导致控制器产生控制作用。通过自动平衡补偿控制算法滤除位移信号中的转速同频分量，即可削弱控制器对由于不平衡量所产生位移量的控制作用，从而只降低转速频率点附近的磁轴承支撑刚度。随着径向磁轴承线圈中的电流大小逐渐趋近稳定，便可以认为此时刚度k≈0 N/m，转子此时围绕其惯性轴旋转。

2 基于Simulink的自动平衡控制仿真分析

本文建立基于Simulink的主动磁悬浮轴承控制系统模型如图3所示。模型中考虑电磁力的非线性、位移传感器误差以及不平衡量大小与转速对系统的影响，并在模型中加入以陷波滤波环节为核心的自动平衡补偿算法。设定转子转速为12 000 r/min(200 Hz)，偏心距e=5 μm。仿真结果如图4～图6所示。其中，图4为滤波前后控制器输入位移信号频谱图。图5为滤波前后轴心轨迹变化情况。图6为滤波前后轴承竖直方向外传力变化情况。

图3 基于Simulink的主动磁悬浮轴承控制系统仿真模型

图4 滤波前后控制器输入位移信号频谱图

图5 轴心轨迹变化情况 图6 轴承竖直方向外传力变化情况

由仿真结果可知：系统在稳定运行0.5 s后开启自动平衡补偿算法，补偿算法开启后，控制器输入端位移信号中的转速同频分量被滤除，转子轴心轨迹半径由10 μm减小至5 μm附近，接近偏心距e，磁轴承外传力幅值也由约15 N降低至5 N左右。

3 小结

针对主动磁悬浮转子不平衡振动的问题，本文首先从理论角度分析了主动磁悬浮振动产生的原因，讨论了自动平衡补偿控制使转子围绕惯性轴旋转的原理，并通过计算得出自动平衡补偿控制在抑制系统振动的同时，可在一定程度上提高磁悬浮轴承转子旋转精度，适合应用于高速磁悬浮系统的控制中。建立了含有自动平衡补偿控制算法的磁悬浮轴承控制系统仿真模型，并通过仿真验证了理论计算的正确性。