二自由度并联机构的逆解算法与性能优化

2021-10-11单东升

机械工程与自动化 2021年5期

牛彪，梁全，单东升

(沈阳工业大学机械工程学院，辽宁沈阳 110870)

0 引言

并联机构是个复杂的运动学和动力学系统，工作能力强、运动精度高、反应速度快，因此有广阔的应用前景[1]。对于并联机构运动学的研究分为正运动学和逆运动学两种[2]，由于正运动学非常复杂难以解决，所以采用逆运动学对二自由度并联机构进行研究。当给定上平台目标位移或角度时通过运动学逆解算法求解出两个液压缸的伸缩位移，进而实现上平台期望的位姿变换。由于并联机构本身存在非线性特性以及不确定因素的扰动影响，使得上平台运动时会出现动作迟缓和位姿精度不高的现象。为解决上述问题，本文对二自由度并联机构采用极点配置进行性能优化，以得到良好的控制效果。

1 二自由度并联机构设计

二自由度并联机构由底座、平台及两组液压系统组成，左液压缸与上平台和底座的连接均为旋转副，右液压缸与底座的链接为固定连接、与上平台的链接为旋转副，如图1所示。

图1 并联系统结构图

2 运动学分析

已知上平台的位姿求解各个支腿的长度叫做位置姿态逆解[3]。为了对上平台的运动进行描述，选取两个坐标系，即底座的静坐标系O-XY和上平台的动坐标系O1-X1Y1[4]。

上平台的运动位姿用广义坐标d=[θ,y](θ为旋转角度，y为位移)来描述，即d1=θ、d2=y。这两个参数确定后，上平台的位姿就能唯一确定。

上平台沿OY轴方向平移y,得到的变换矩阵T1为：

(1)

上平台在O-XY平面内转动θ角，得到的变换矩阵T2为:

(2)

上平台的铰点坐标由动坐标系变换到静坐标系下的齐次变换矩阵T为:

T=T2·T1.

(3)

上平台运动时在静坐标系中的速度vp和加速度ap分别为:

(4)

(5)

上平台运动时在静坐标系中的角速度ωp和角加速度εp分别为:

(6)

(7)

在动坐标系中用4×2阶矩阵A表示上平台的两个铰点坐标，齐次坐标描述为:

(8)

在静坐标系中用4×2阶矩阵B表示底座的两个铰点坐标，齐次坐标描述为:

(9)

初始位置时，上平台的铰点在动坐标系和静坐标系下的坐标值不变；运动时，上平台的铰点在静坐标系中的坐标值发生了改变。设上平台的铰点在静坐标系中的坐标C为:

C=T·A.

(10)

两组液压缸活塞的伸缩位移由连接液压缸上、下铰点之间的距离Li(i=1,2)减去液压缸初始长度L0来确定：

(11)

其中：cki为矩阵C的各个元素；bki为矩阵B的各个元素。

对式(11)求导可以求得液压缸的速度：

(12)

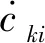
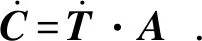
(13)

对式(12)求导可以求出液压缸的加速度：

(14)

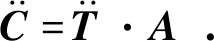
(15)

3 极点配置

液压系统是二自由度并联机构的驱动器，对液压系统进行极点配置控制，最终可实现机构的性能优化。

3.1 阀控缸的基本方程

(1)滑阀的流量方程：

qL=kqxv-kcpL.

(16)

其中：qL为负载流量；kq为流量增益；xv为阀芯位移；kc为流量压力系数；pL为负载压力。

(2)液压缸流量连续性方程：

(17)

其中：Ap为液压缸有效作用面积；xp为液压缸活塞的位移；Ctp为液压缸总泄漏系数；Vt为液压缸总体积；βe为液压缸体积弹性模量。

(3)液压缸力平衡方程：

(18)

其中：mt为活塞及负载折算到活塞上的总质量；Bp为活塞及负载的黏性阻尼系数；KL为负载弹簧刚度；FL为作用在活塞上的外负载力。

液压缸几乎没有泄漏，总泄漏系数Ctp=0；液压缸体积弹性模量βe=7×108Pa；不给系统加外负载，因此KL=0、FL=0；液压油密度为850 kg/m3；流量压力系数kc=1.4×10-8；流量增益kq=2.385 5；活塞及负载折算到活塞上的总质量mt=1 000 kg；液压缸腔体的有效长度L=1 m；液压缸有效作用面积Ap=4.908 7×10-4m2；液压缸总体积Vt=4.908 7×10-4m3；阻尼系数Bp=0.001。

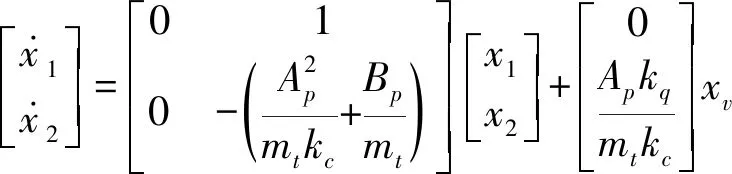
(19)

对式(19)进行如下的能控性判定：

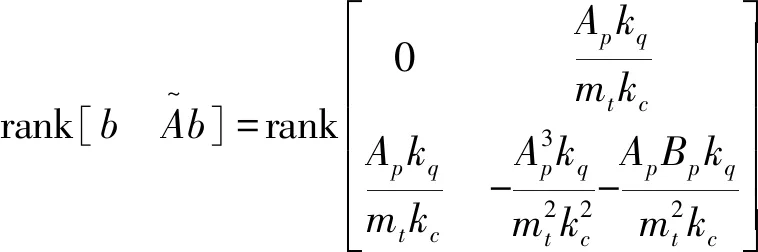
(20)

3.2 极点配置算法

其中：I为单位矩阵；a1，…，an为系数。

(2)求闭环系统的期望特征多项式：

(3)计算：

(4)计算：

(5)求P=Q-1。

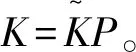
4 Visual Studio与AMESim联合仿真

应用Visual Studio与AMESim联合仿真，用C语言对极点配置算法进行编程，在AMESim中搭建并联机构仿真模型,如图2所示。

图2 AMESim中搭建的并联机构仿真模型

用C语言编写的极点配置算法程序与AMESim模型之间进行数值交换的程序如下：

setplace1 =output[6];

setplace2 =output[7];

dstatevalue1[0][0] =output[2];

dstatevalue1[1][0] =output[3];

dstatevalue2[0][0] =output[4];

dstatevalue2[1][0] =output[5];

input[2] =-(output[6] * L-k1[0][0] * dstatevalue1[0][0] -k1[0][1] * dstatevalue1[1][0]);

input[3] =-(output[7] * L-k0[0][0] * dstatevalue2[0][0] -k0[0][1]*

dstatevalue2[1][0]);

input[0] =output[0];

input[1] =output[1];

程序中：output[0]、output[1]为采样时间，output[2]为左边液压缸的位移反馈值，output[3]为左边液压缸的速度反馈值，output[4]为右边液压缸的位移反馈值，output[5]右边液压缸的速度反馈值，output[6]为上平台期望旋转角度值，output[7]为上平台期望位移值，input[2]为输入左边比例阀的值，input[3]为输入右边比例阀的值，dstatevalue1[0][0]、dstatevalue1[1][0]为左边阀控缸系统的状态变量，dstatevalue2[0][0]、dstatevalue2[1][0]为右边阀控缸系统的状态变量，K1、K0分别为左、右两液压缸的状态反馈增益矩阵。