鼓泡箔片动压气体径向轴承库仑阻尼耗散的数值分析
2021-10-11赵琪侯予任雄豪陈双涛赖天伟
赵琪,侯予,任雄豪,陈双涛,赖天伟
(西安交通大学能源与动力工程学院,710049,西安)
气体箔片轴承是一种弹性表面的自作用式气体动压轴承。由于其具有稳定性高、环境污染低和工作转速快等优点[1],被广泛应用于高速轻载的旋转机械中,如车载燃料电池空压机、低温透平膨胀机、空气循环机和微型透平机械等[2-4]。目前较为常见的轴承结构包括悬臂型、多楔型、波箔型和鼓泡型等[5-6]。
目前国内外对气体箔片轴承的研究主要集中在热管理、箔片涂层、静态特性、动态特性以及转子动力学分析等,针对气体箔片轴承的库仑阻尼耗散的研究虽有一定成果但总体而言仍比较少。箔片轴承在高转速下运行时,阻尼是影响其稳定性的一个关键因素[7],库仑阻尼耗散的求解则是气体箔片轴承性能分析的核心问题。气体箔片轴承通过库仑阻尼耗散吸收不稳定涡动能量,转子振幅减小,使得其所支承的高速旋转机械在一定的振动冲击和涡动范围内保持良好的稳定性[8]。1975年Walowit等根据波纹箔片和轴承座之间不同摩擦因数和各种波纹拱形角度推导载荷挠度的关系式,最早给出了单个波纹箔片的刚度计算公式[9]。2013年徐方程等研究了库仑摩擦效应对波纹箔片刚度特性的影响规律[10]。Zywica等在分别考虑动摩擦和静摩擦的情况下对波箔轴承的阻尼特性进行了研究,并将数值模拟和实验结果进行了验证[11]。Arghir等提出了一种简化的波箔变形模型,考虑了箔片间隙和库仑摩擦的相互作用,使数值模型更接近于实际情况[12]。
从2008年开始,西安交通大学开展了单层鼓泡型箔片轴承的理论及实验研究[13],之后进一步提出了具有优异性能的鼓泡型多层弹性箔片动压气体轴承新结构,图1所示为双层鼓泡箔片动压径向轴承[14]。目前对鼓泡箔片轴承的研究主要集中在实验方面[15-16],理论研究大多是关于静态参数和动态性能的数值计算,如承载力、偏位角、动态刚度和阻尼系数分析等[17-20],鼓泡箔片轴承的库仑阻尼耗散研究还不全面。为了研究鼓泡轴承的动态特性与稳定性,本文采用基于能量耗散的思想评价鼓泡箔片轴承阻尼[21],进而对鼓泡箔片轴承的库仑阻尼进行了分析。

图1 双层鼓泡箔片动压径向轴承Fig.1 Double-layer protuberant foil journal bearing
1 结构与数值模型
1.1 鼓泡箔片轴承结构模型
根据鼓泡箔片的结构特点,本文将箔片简化为薄板模型。图2所示为双层鼓泡箔片轴承变形示意图。图2a表示施加压力前箔片相对位置关系,图2b为顶层平箔受到压力作用产生变形的示意图,图2c表示由于中层鼓泡箔片发生形变引起顶层平箔产生附加位移。

(a)初始位置示意图
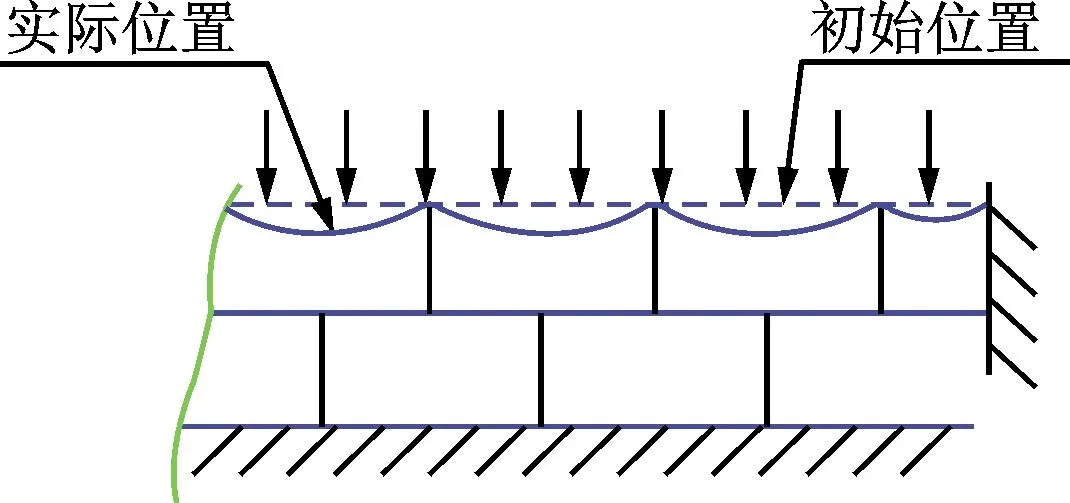
(b)平箔受力变形示意图

(c)平箔和鼓泡箔片变形示意图图2 双层鼓泡箔片轴承变形示意图Fig.2 Deformation diagram of double-layer protuberant foil bearing
1.2 鼓泡箔片轴承数值模型
本模型中假设箔片只在周向发生滑移,图3a所示为周向方向弹性单元相对位置关系。不考虑轴向方向滑移量,为了计算单个鼓泡支承点相对滑移量,弹性单元位移分析如图3b和图3c所示。弹性单元间距为S,弹性单元平衡后,假设顶层平箔沿Y方向产生位移δy,平箔右支承点X方向对应的相对滑移量为δx,α和β为平箔变形前与变形后位移夹角,根据几何关系其表达式如下
δx=X1+X2-S
(1)

(a)周向弹性单元相对位置图

(b)弹性单元平衡位置图
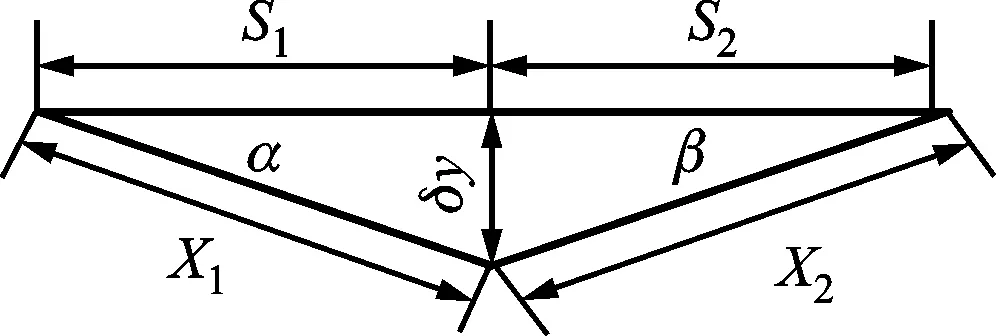
(c)箔片相对位移图图3 箔片位移示意图Fig.3 Schematic diagram of foil displacement
其中
(2)
平箔第一个弹性单元右支承点由于摩擦产生的能量为E1=μF1δx1,其中F1为支承点正压力。为了简化模型,本文只考虑动摩擦力,不考虑静摩擦力。μ根据文献[22]模型(Heshmat公式)进行选取,μ=f/N,其中f为动摩擦力,N为接触点正压力。
相应地,其他支承点上由于摩擦产生的能量可以用同样的方法求解。不同的是,当支承点靠近自由端时,由于箔片滑移量的累加,其支承点相对滑移量为其弹性单元滑移量与固定点之间所有弹性单元相对滑移量之和。因此,平箔耗散能量E为
μ(F1δx1+F2δx2+F2δx2+…+Fnδxn)
(3)
同样,鼓泡箔片库仑阻尼耗散能量也可以采用类似的方法进行计算。本文基于有限元2D薄板单元模型将顶层平箔片与中层鼓泡箔片简化为2D弯曲板,使用矩形弯曲板单元对顶层平箔与中层鼓泡箔片进行离散从而计算箔片y方向变形量δy。假设鼓泡支承点只提供弹性支承且不发生变形,则鼓泡箔片可按平箔片处理。计算域通过四节点矩形单元离散,每个节点的力约束条件和位移自由度如图4所示。P为每个单元所受载荷,θxk和θyk为节点转角大小,wk为节点位移大小,Mxk和Myk为节点所受力矩,Fk为节点受力(k=m,n,i,j)。薄板尺寸为长78.5 mm,宽25 mm,网格密度为36×20。模型中材料为铍青铜和Inconel合金。平箔片与鼓泡箔片都有一端固定在轴承座上,属于0位移的边界条件;由于上层箔片与下层箔片的接触点位移相同,因此下层箔片鼓泡点的位移作为上层箔片的附加位移边界条件;由于下层箔片存在变形位移,因此属于非位移的边界条件。模型的正确性已在课题组2016年发表的论文(文献[6])中得到了验证。

(a)简化的顶箔矩形单元

(b)节点位移分析

(c)节点力分析图4 有限元矩形单元示意图Fig.4 Schematic diagram of finite rectangular element
箔片轴承阻尼分为结构阻尼和干摩擦阻尼,结构阻尼相对于干摩擦阻尼较小。通常研究以干摩擦阻尼为主,本文主要研究的是鼓泡箔片轴承中由于箔片摩擦引起的库仑摩擦阻尼。在定摩擦因数条件下,库仑摩擦阻尼大小只与箔片所受压力有关。本文先分析了无量纲均布压力P=p/p0(p0为大气压)条件下箔片结构参数与库仑阻尼耗散的关系,进而在耦合气膜压力下研究了转速和偏心率对库仑阻尼耗散的影响。
2 结果分析与讨论
2.1 均布压力条件下平箔片厚度对库仑阻尼耗散的影响
当平箔片厚度较小时,箔片变形量较大,箔片间相对滑移量会发生变化从而导致库仑阻尼发生改变。从图4可以看出:随着平箔片厚度增大,单层和双层鼓泡箔片轴承库仑阻尼耗散能量均出现减小的趋势;当平箔片厚度增大到一定程度时,库仑阻尼耗散能量减小趋势放缓并逐渐趋于定值。当无量纲均布压力增大时,平箔片厚度变化对库仑耗散能量的影响更加明显,这也说明平箔片厚度变化在大载荷时对箔片轴承库仑阻尼耗散影响更加显著。通过图5a和图5b的对比发现,在无量纲均布压力为1.6、平箔片厚度为0.07 mm时,双层和单层鼓泡轴承耗散能量分别为100 μJ和55 μJ,双层鼓泡箔片轴承的库仑阻尼耗散远大于单层鼓泡箔片轴承。这说明双层鼓泡箔片轴承相比于单层鼓泡箔片轴承更容易通过库仑摩擦力耗散能量。分析图6可知:双层鼓泡箔片轴承改变中层鼓泡箔片厚度耗散能量效果优于改变顶层平箔厚度。
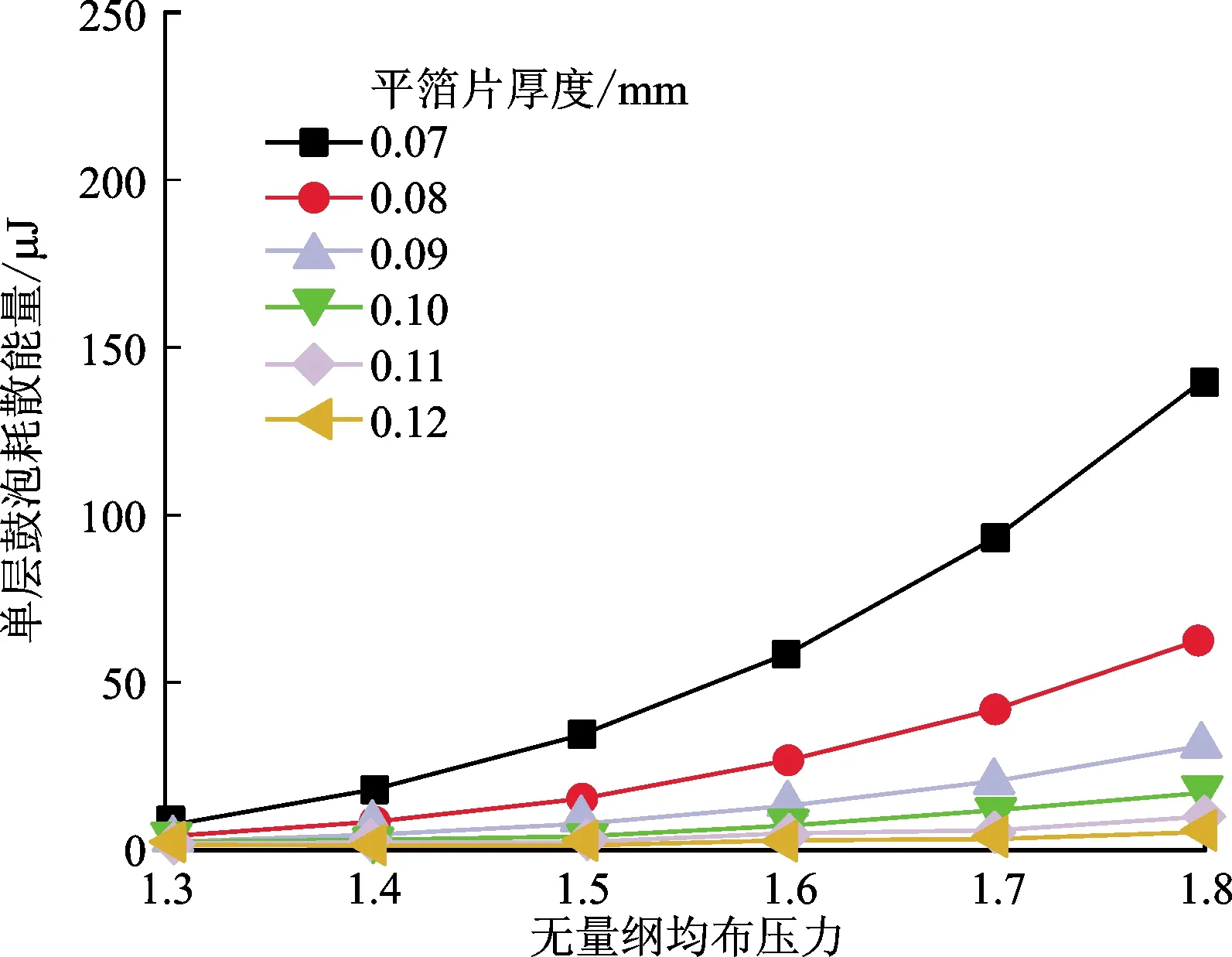
(a)单层鼓泡轴承平箔片厚度变化

(b)双层鼓泡轴承平箔片厚度变化图5 箔片厚度对耗散总能量的影响Fig.5 Influence of foil thickness on the total energy dissipation

(a)平箔片厚度变化
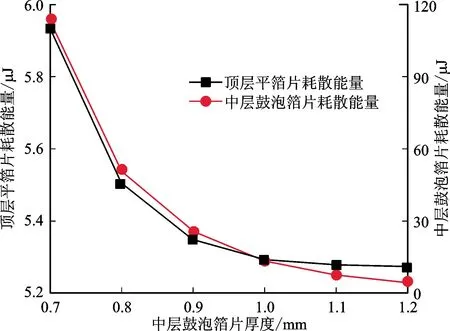
(b)中层鼓泡箔片厚度变化图6 双层鼓泡轴承箔片厚度对耗散能量的影响Fig.6 Influence of the thickness of the double-layer protuberant bearing foil on the energy dissipation
2.2 均布压力条件下轴向间距和周向间距对库仑阻尼耗散的影响
滑移方向鼓泡支承点越密集,箔片变形量的减小使得鼓泡箔片轴承支承刚度提高越显著;同时由于箔片滑移量减小,库仑阻尼耗散能量也会相对减小。从图7可以看出:周向鼓泡节点间距增大时,箔片滑移量变大,箔片库仑阻尼耗散明显增大;周向间距减小时,耗散能量逐渐减小。这说明选择鼓泡轴承箔片参数时,应综合考虑箔片参数对轴承刚度和阻尼系数的影响,以求满足工作条件。图8展示了鼓泡支承点轴向间距对库仑阻尼耗散能量的影响。鼓泡支承点轴向间距越小,支承点越密集,总的耗散能量就越多。当轴向间距相对较大时,库仑阻尼耗散能量趋近于定值。

图7 周向间距对库仑阻尼耗散能量的影响Fig.7 Influence of the circumferential pitch on the energy dissipation of Coulomb damping

图8 轴向间距对库仑阻尼耗散能量的影响Fig.8 Influence of the axial pitch on the energy dissipation of Coulomb damping
2.3 均布压力下箔片材料特性对库仑阻尼耗散的影响
由于不同材料的特性不同,其刚度和阻尼特性也有明显差异,所以要综合考虑材料属性对鼓泡箔片轴承耗散能量的影响。从图9可以看出:在定摩擦系数下,双层鼓泡箔片轴承选用铍青铜时库仑阻尼耗散能量最大,单层鼓泡箔片轴承选用Inconel合金时库仑阻尼耗散能量最小。这是由于Inconel合金刚度大,箔片滑移量减小,其库仑阻尼耗散量也相对较小。对比实验数据也可以发现同样的规律。从图10中可以看出:两种径向鼓泡箔片轴承都有近似线性的刚度特性。根据载荷位移曲线计算的斜率表明,PGFB-QBe1.7(双层铍青铜鼓泡箔片轴承)和PGFB-0Cr18Ni9(双层不锈钢鼓泡箔片轴承)结构刚度分别约为0.3×106N/m和0.5×106N/m。可见径向轴承PGFB-0Cr18Ni9的结构刚度比PGFB-QBe1.7要大一些,这与不锈钢0Cr18Ni9的弹性模量较大有关。采用平行四边形的面积近似计算载荷-位移循环的功耗。经计算,径向鼓泡箔片轴承PGFB-QBe1.7在一个载荷位移循环内的功耗为4.5×10-4J,而PGFB-0Cr18Ni9在一个载荷位移循环内的功耗为2.9×104J。这也表明径向鼓泡箔片轴承PGFB-QBe1.7的阻尼远大于径向鼓泡箔片轴承PGFB-0Cr18Ni9的阻尼。符合材料刚度变大在一定程度上导致库仑阻尼耗散减小的规律。
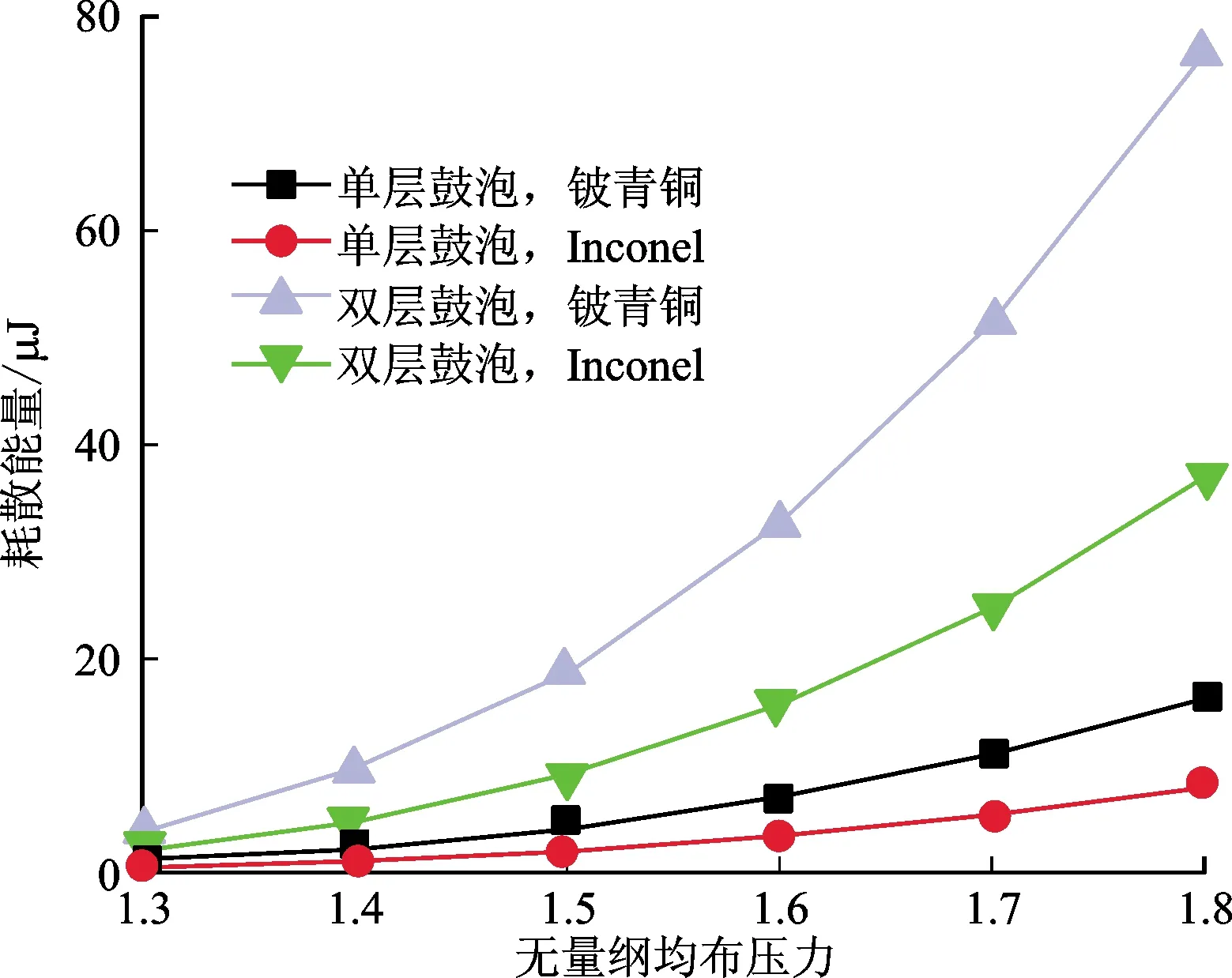
图9 材料对库仑阻尼耗散能量的影响Fig.9 Effects of materials on the energy dissipation of Coulomb damping

(a)PGFB-QBe1.7
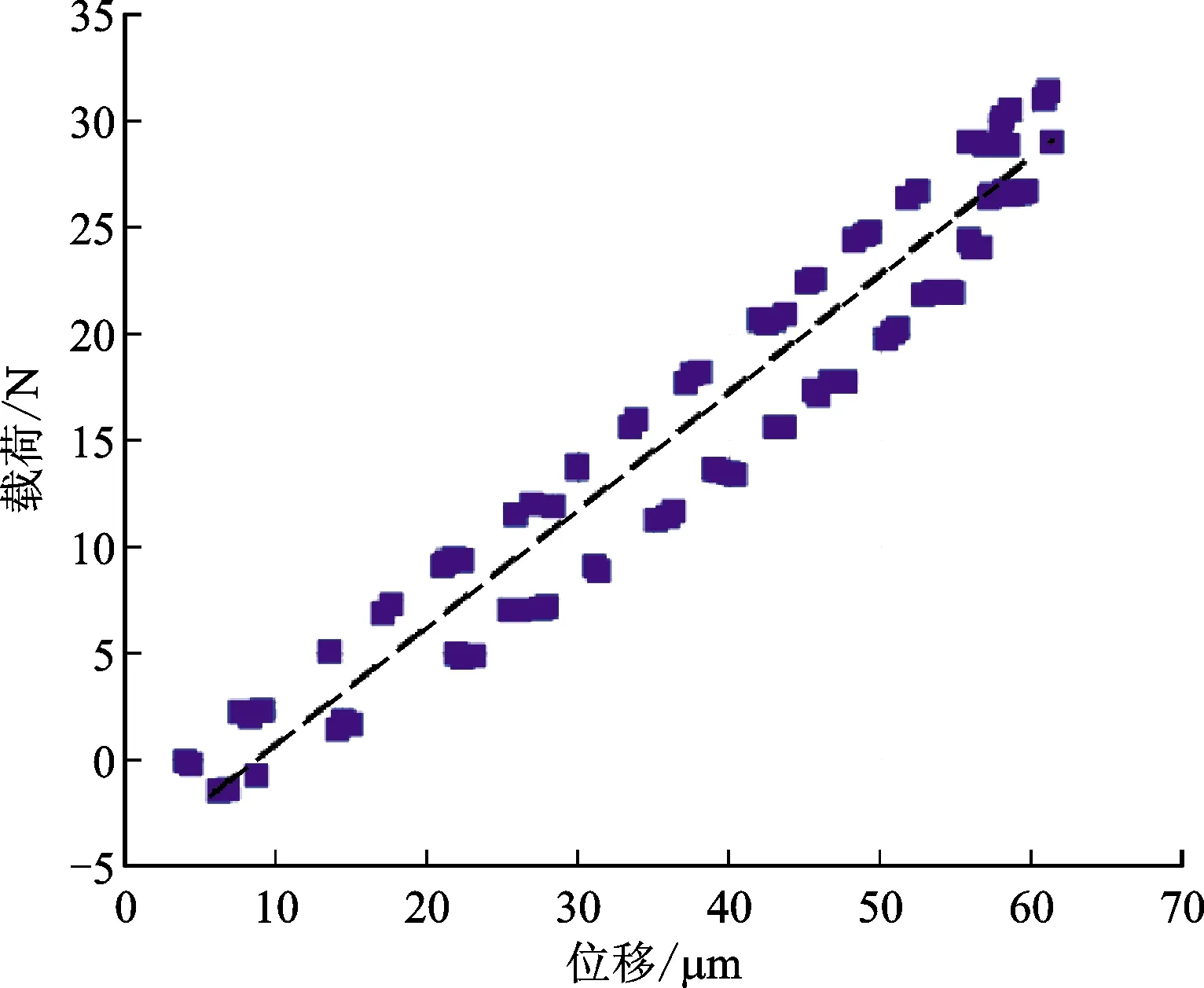
(b)PGFB-0Cr18Ni9图10 径向双层鼓泡箔片轴承的载荷-位移实验测试结果Fig.10 Load-displacement test results of radial double-layer protuberant foil journal bearing
2.4 耦合气膜压力下鼓泡轴承耗散能量分析
实际运行过程中,气膜压力和箔片弹性变形存在双向耦合,通过迭代求解耦合气体Reynolds方程可得到实际压力分布。从图11可以看出,随着偏心率增大和转速升高,库仑阻尼耗散能量大幅增加。与施加均布压力不同,在耦合气膜压力作用下,由于只有正压区在压力作用下可以通过库仑阻尼耗散能量,所以总的耗散能量远小于施加均布压力时的耗散能量。
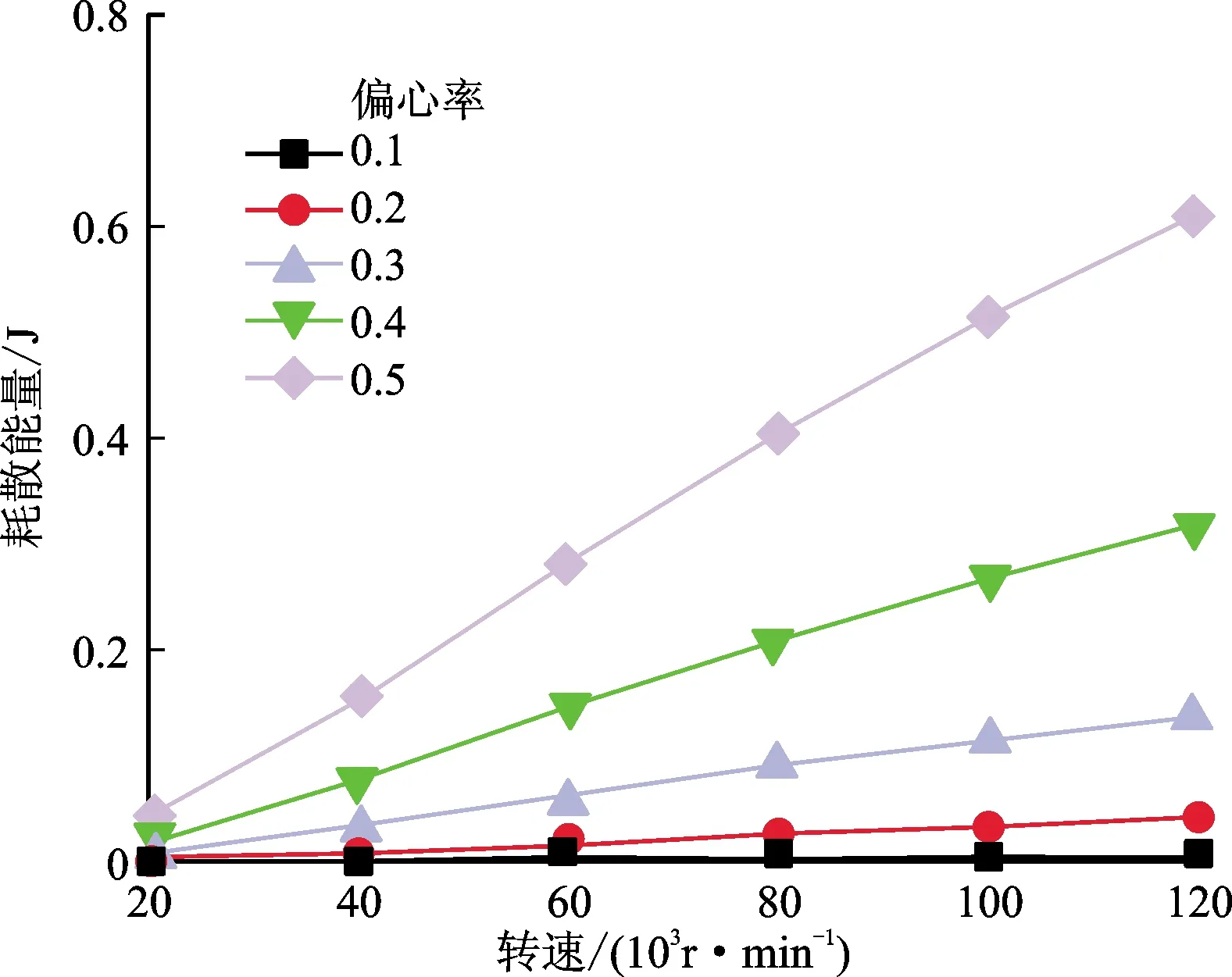
图11 双层鼓泡箔片轴承偏心率对耗散能量的影响Fig.11 Effect of the eccentricity of double-layer protuberant foil bearing on the energy dissipation
3 结 论
本文采用能量耗散法对鼓泡箔片动压气体轴承的库仑阻尼耗散能量进行分析,得到的结论如下。
(1)随着平箔片厚度增大,单层和双层鼓泡箔片轴承库仑耗散能量均出现减小的趋势。当平箔片厚度增大到一定程度时,库仑阻尼耗散能量减小趋势放缓并逐渐趋于定值。在相同工况下,双层鼓泡箔片轴承的库仑阻尼耗散明显大于单层鼓泡箔片轴承,且双层鼓泡箔片轴承改变中层鼓泡箔片厚度耗散能量效果优于改变顶层平箔厚度。
(2)周向鼓泡间距增大时,箔片滑移量变大,箔片库仑阻尼耗散能量明显增大。鼓泡支承点轴向间距越小,轴向支承点越密集,总的库仑阻尼耗散能量越大,越有利于抑制高速转子的涡动,从而进一步提高动压箔片轴承的稳定性。
(3)高弹性模量材料的硬度更高,箔片滑移量较小,会减小库仑阻尼耗散能量。相同工况下,鼓泡箔片轴承选用高弹性模量材料其库仑阻尼耗散能量更小。
(4)随着偏心率增大和转速升高,库仑阻尼耗散能量大幅增加。这说明鼓泡箔片轴承具有很好的稳定性。
