离心压缩机尺寸效应修正模型

任昊,罗金平,牛大勇,孙玉莹,刘立军

(1.西安交通大学能源与动力工程学院,710049,西安;2.沈阳鼓风机集团股份有限公司,110869,沈阳)

工程实际中,离心压缩机常通过模化法来设计。模化法的理论基础为相似理论,完全相似条件包括几何相似、运动相似、动力相似及热力相似。现实中,产品离心级与基准离心级的雷诺数不同,导致二者不满足完全动力相似,尤其当雷诺数小于临界雷诺数时,流动未进入自动模化区,此时雷诺数的不同引起的性能偏差相当显著。同时,密封间隙、叶顶间隙、叶片厚度、表面粗糙度等很难满足完全几何相似,也会导致产品级与基准级之间存在性能偏差。由于以上完全相似条件无法严格满足,因此由基准级模化缩放而得到的产品级的气动性能与基准级不完全相同。模化设计中,产品级与基准级之间的这种性能偏差被称为离心压缩机的尺寸效应。因此,研究离心压缩机尺寸效应并对其进行修正,具有重要意义。由于叶片厚度只有在少数情况下不满足完全几何相似,而密封间隙、叶顶间隙偏离几何相似的程度并无固定的规律可循,需要根据转子动力学计算结果以及轴承间隙等具体结构参数来确定。因此,为使研究更具普遍性,本文以雷诺数和粗糙度为两大主要因素来研究并修正离心压缩机的尺寸效应。

目前,针对离心压缩机性能尺寸效应,文献[1-9]通过性能实验观测、计算流体动力学(CFD)等手段进行了定性研究。而关于离心压缩机性能尺寸效应的定量修正研究[10-17]主要包括:1955年Pfleiderer通过类比光滑圆管充分发展流动实验给出了雷诺数引起离心压缩机效率偏移的经验修正公式[10];2011年,Casey和Robinson通过类比粗糙平板流动实验,提出了雷诺数及相对粗糙度引起离心压缩机效率及流量系数偏移的经验修正公式[12]。2013年,Pelz和Stonjek通过离心压缩机性能实验数据及类比粗糙圆管流动实验,拟合出了效率修正公式,然后通过效率主曲线假设,得到了流量系数修正公式[13]。

综上,目前对于离心压缩机尺寸效应的定量修正研究偏少,已有的研究多将离心级内的流动简化类比为圆管或平板流动,从而得到性能修正公式的基本形式,再通过有限的实验来测定公式中的经验系数。通过以上方法获得的修正公式缺乏物理直观性,相关经验系数物理含义不明确。为此,本文将直接以离心级为研究对象,主要考虑雷诺数和相对粗糙度对离心压缩机性能的影响,提出修正模型,以理论推导为主要手段,获得离心压缩机模化设计中效率及流量系数修正方程,并赋予修正系数明确的物理意义,从而减少对经验因素的依赖。

1 理论分析及修正模型

产品级效率及其对应的基准级效率分别用η和ηm表示,其中下标m表示基准级。雷诺数和相对粗糙度引起的效率偏移分别用修正因子θ1与θ2来表示。当仅考虑雷诺数的影响时,产品级效率η1与对应的基准级效率ηm满足

η1=θ1ηm

(1)

当仅考虑相对粗糙度的影响时,产品级效率η2与对应的基准级效率ηm满足

η2=θ2ηm

(2)

当同时考虑二者的影响时,产品级效率η与对应的基准级效率ηm满足

η=θ1θ2ηm

(3)

1.1 离心压缩机模化设计中的效率偏移

首先,我们针对雷诺数引起的效率偏移(即修正因子θ1)进行研究。由于雷诺数主要表征流动受黏性影响的大小,因此可以将离心级中的能量损失分为黏性损失和非黏性损失2大类,其中由于流体黏性而产生的能量损失总和称为黏性损失(如轮阻损失、涡流损失等),而除此之外的能量损失总和称为非黏性损失(如泄漏损失、部分激波损失等)。然而,离心级中的实际流场十分复杂,有诸如分离涡、激波等复杂流动结构,难以直接从理论上进行严格的数学推导,为此本文提出如下2个简化假设:

(1)离心级在模化前后,级中的黏性损失不随总功耗等比例变化,非黏性损失随总功耗近似等比例变化;

(2)离心级中所有黏性损失均存在于边界层内,边界层内流体不可压。

在此假设下,构造一组满足相似条件且进口状态相同的产品级与基准级,特征尺寸分别为L和Lm,其模化比为L/Lm,雷诺数分别为Re和Rem。对于这样一组产品级与基准级,由相似条件及透平压缩机欧拉方程可得

(4)

式中,Wth和Wth,m分别为产品级与基准级的理论功。结合假设(1),又考虑到离心级的总功耗主要为理论功,近似有关系

(5)

式中:W和Wm分别为产品级与基准级的总功耗;Wn-vis和Wn-vis,m分别为对应的非黏性损失。由于边界层相对于流体域足够薄,边界层内的流体质点距离壁面足够近,因此可近似地将离心级流道壁面上任一面积元dS处的边界层流动等同于无限大不可压缩平板边界层流动。边界层厚度为δ,由无限多层流质单元构成,主流速度用U表示,层内表观动力黏性系数为μ,并假设层内的速度分布为二次抛物线形式。利用牛顿内摩擦定律积分得出面积元dS处对应的边界层内的黏性耗散功率P为

(6)

考虑到不可压缩平板边界层Navier-Stokes方程中黏性项与惯性项量级相等,因此有

(7)

式中,δ和δm分别为产品级与基准级的边界层厚度。联立式(6)和式(7),结合几何相似条件可得

(8)

式中:Wvis和Wvis,m分别为产品级与基准级的黏性损失。

定义:基准级中的黏性损失在其总功耗中的占比为基准级的黏损比函数Xm,表示为

(9)

联立式(1)(5)(8)及式(9),并结合效率的物理含义可得

(10)

综上,式(10)即为本文得到的离心压缩机模化设计中由于雷诺数不同而引起的效率偏移修正因子θ1的表达式。由式(10)可知:当模化比L/Lm大于1时,产品级效率高于基准级;反之,产品级效率低于基准级,这与定性研究结果相符合[1-9],初步显示了本修正模型的合理性。由本文定义的基准级黏损比函数Xm的物理含义,可将其表示为基准级的流量系数φm与叶轮出口直径Dm的二元函数Xm=Xf(φm,Dm),其具体形式可以由实验研究或者数值计算获得。若采用实验研究,实验量及成本巨大。因此,本文将利用数值模拟获得基准级黏损比函数Xm的具体表达式。

对于修正因子θ2的确定,将通过后文的数值模拟计算,得到在雷诺数不变的情况下,不同相对粗糙度引起的离心级效率缩放比例η2/ηm,进而拟合出修正因子θ2的具体表达式。

1.2 离心压缩机模化设计中的流量系数偏移

当流体通过一根内壁粗糙的圆管通道时,内部流场的情况如图1a所示,由于实际壁面的粗糙元往往非常密集,因此相邻两粗糙元之间的流体被截留形成细小旋涡,粗糙元上方通过的流体跟被截留流体之间仅有少量动量交换,基本上无质量交换。所以粗糙度对通道内流动的阻塞作用,可等效为缩小流道流通直径,如图1b所示。这就是清华大学杜东兴博士与过增元院士于2000年提出的流道收缩效应模型[18],他们估计流道实际通流直径相对于流道几何直径d的减小量为粗糙元高度Ra的2倍,即等效通流直径为

de=d-2Ra

(11)

(a)实际流态

(b)等效流动图1 流道收缩效应模型Fig.1 The model of flow path shrinkage effect

上述模型只考虑了粗糙度对通流的阻塞影响,没有考虑黏性边界层对通流能力的影响。为此,本文在原模型基础上,同时考虑黏性边界层对流动产生的阻塞效应,改进了流道收缩效应模型,如图2所示,则等效通流直径为

de=d-2Ra-2δ*

(12)

图2 流道收缩效应改进模型Fig.2 The improved model of flow path shrinkage effect

在二次抛物线速度分布假设下,边界层排挤厚度δ*为

(13)

同时考虑了粗糙度和黏性边界层影响的等效通流直径de为

(14)

对离子压缩机而言,用离心级入口截面的水力直径d来表征其流道几何直径。引入流量系数来表征离心级通流能力的大小,定义离心级流量系数φ为

(15)

式中:Qv为离心级入口体积流量;D为叶轮出口直径;u为叶轮出口圆周速度。对此组产品级与基准级(前文1.1小节中构造),显然有

(16)

式中:Qv和Qv,m分别为产品级与基准级的入口体积流量,de和de,m分别为产品级与基准级的等效通流直径。

联立式(7)(14)(15)及式(16),结合离心压缩机相似条件,可得模化设计中离心压缩机流量系数的修正方程为

(17)

式中:φ和φm分别为产品级与基准级的流量系数;δm为基准级流道内边界层名义厚度;d和dm分别为产品级与基准级入口截面的水力直径;产品级与基准级具有相同的粗糙度Ra。

由式(17)可知:当模化比L/Lm大于1时,有φ>φm,即产品级的通流能力大于基准级;反之,产品级的通流能力小于基准级。

2 数值计算

2.1 雷诺数引起的性能尺寸效应

2.1.1 数值模型与计算条件 如图3所示,本文采用的几何模型为三元离心级,由离心叶轮、扩压器、弯道、回流器这4大主要部分构成。计算中采用了流量系数不同的6组模型级,分别编号为1、2、3、4、5、6号模型级,针对每组模型级分别计算6个不同叶轮出口直径D,分别为200、300、400、500、600、800 mm,各不同叶轮出口直径下的工况互为相似。以上计算对应的模化比范围为:0.25～4.0。

图3 离心级结构Fig.3 Structure of centrifugal stage

本文采用NUMECA FINE/TURBO对离心级进行单通道定常数值模拟,采用S-A湍流模型,数值求解三维雷诺平均N-S方程。S-A湍流模型,具有求解量小、计算准确度高等优点[19]。空间项使用二阶精度的中心差分格式,并采用完全多重网格技术加快计算收敛。计算域网格为全结构化三维网格,如图4以D=500 mm的1号模型级为例,给出了网格示意图。对靠近壁面区域的网格进行加密处理,其中靠近壁面的第一层网格厚度均设为0.005 mm,以保证能捕获边界层内部的流动状况。压缩工质为空气,入口设置为轴向进气,入口空气状态设定滞止温度为30 ℃、滞止压力(总压)为1×105Pa;固壁边界均设置为光滑、绝热、无滑移边界,出口条件设为定质量流量。所有工况经过4 000步以上的迭代计算,当全局残差小于10-4量级,进出口质量流量相对误差均小于0.1%,效率、压比曲线趋于恒定时,认为计算达到了收敛[20]。

图4 模型网格Fig.4 Generated grid of the model

2.1.2 模型验证 本文以D=500 mm的1号模型级为例,做了网格无关性验证并与实验进行对比,如图5所示。可以看出,当网格节点数N大于360×104后,多变效率ηpol与压比ε趋于定值,认为满足网格无关。为节省计算成本,其余尺寸级的网格节点数依此进行适当调整。如图6所示,可以看出压比、效率的计算值和实验值在趋势上吻合较好,计算曲线的高效点流量系数值与实验值也相符,且高效点附近的压比及效率相对误差均在4%以内,因此,本文的数值建模和计算结果是可靠的。

图5 网格无关性验证Fig.5 Verification of grid independence

图6 计算值与实验值比较Fig.6 A comparison between calculated values and measurements

2.1.3 计算结果 图7为1号模型级在不同叶轮出口直径D下的多变效率计算曲线。可以看出向大尺寸模化时,效率曲线呈现上移规律,其余5组模型级规律类似。同时计算得1～6号模型级的高效点流量系数φh如表1所示。

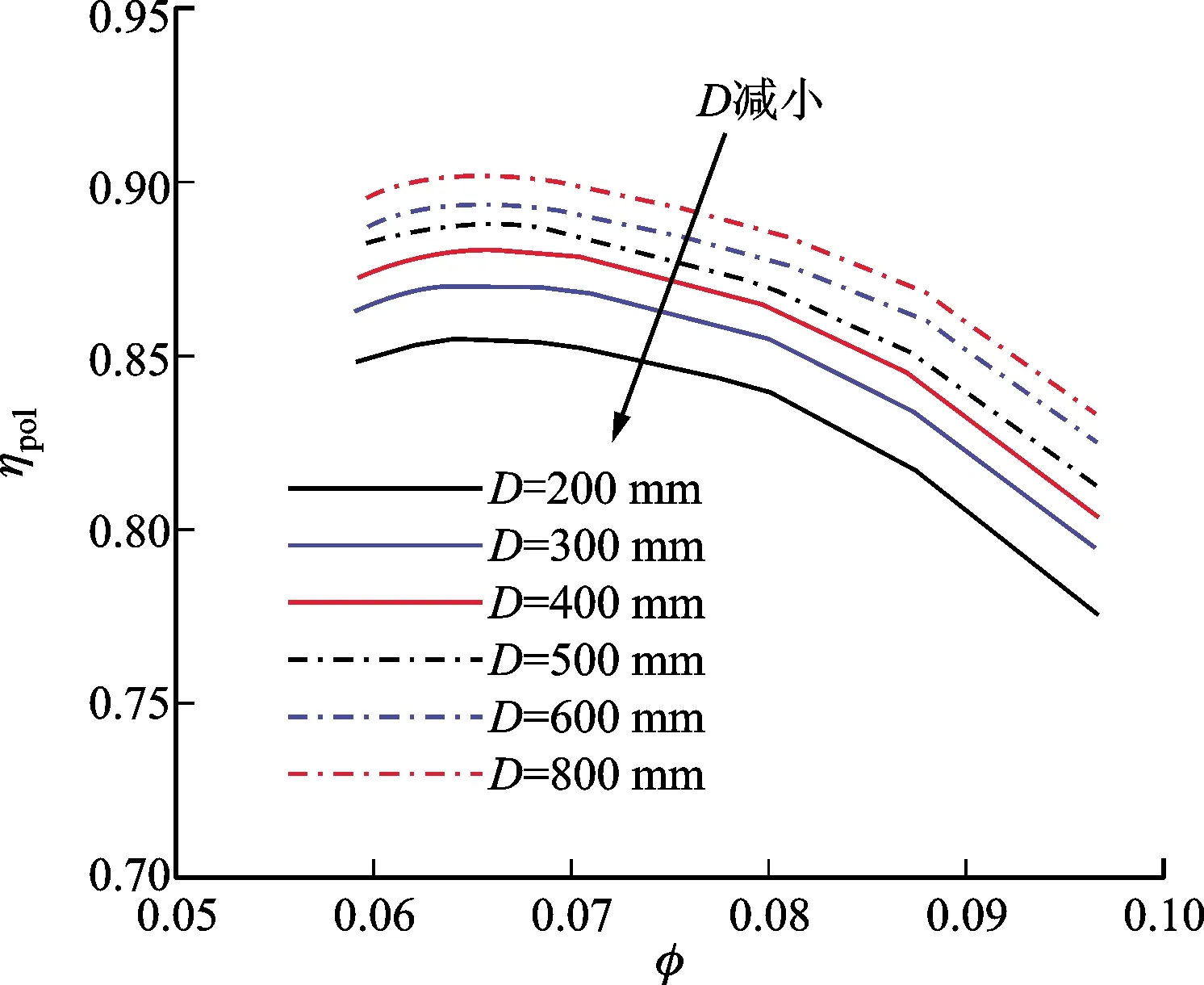
图7 1号模型级多变效率曲线Fig.7 Polytropic efficiency curves of model 1

表1 1～6号模型级的高效点流量系数计算值Table 1 Calculated values of flow coefficient at high efficiency point of model 1 to 6

图8以1号、3号及6号模型级为例,给出了不同参数模型级尺寸效应的对比,可以看出:小流量系数级,效率随尺寸变化更明显;对于同一组模型级,小尺寸级的效率偏移更显著。这是因为小流量系数级的流道更狭窄,边界层相对更厚,因而尺寸效应更明显;小尺寸级的雷诺数更小,流动受黏性的影响更大,因而尺寸效应更明显。这同时印证了前文的理论判断:Xm=Xm(φm,Dm)。

图8 不同参数模型级尺寸效应的对比Fig.8 A comparison of scale effects with different parametric stages

图9以1号和2号模型级为例,给出了不同尺寸下高效点流量系数变化的情况,可以看出:随着模型级向大尺寸模化,流量系数增大;反之,流量系数减小。

图9 流量系数的偏移Fig.9 Deviations of flow coefficient

以1号模型级为例,在其叶轮出口附近、扩压器、回流器处分别选取了3个监测截面(如图3所示)。图10a～10c分别给出了不同尺寸级叶轮出口处(图3中监测截面1)流道中的子午速度Vm、比熵产s及多变效率ηpol随距离轴盘侧壁面的无因次距离l变化的分布曲线。由图10a可以看出,在近壁面处速度分布近似抛物线形状,体现出了明显的边界层流态,与前文(1.1节)中的假设相吻合;且级尺寸越小,边界层相对越厚(边界层厚度δ定义为99%U处到壁面的距离,从图10a估计δ约为流道宽度的5%),因此级通流能力越小,与图9的现象相符合。由图10b可以看出,高熵产区在近壁面处,说明级内的不可逆损失主要集中在边界层内,且级尺寸越小,损失相对越大。如图10c所示:级尺寸越小,效率越低。对于图3中截面2、3处也有类似的规律。

(a)子午速度

(b)比熵产

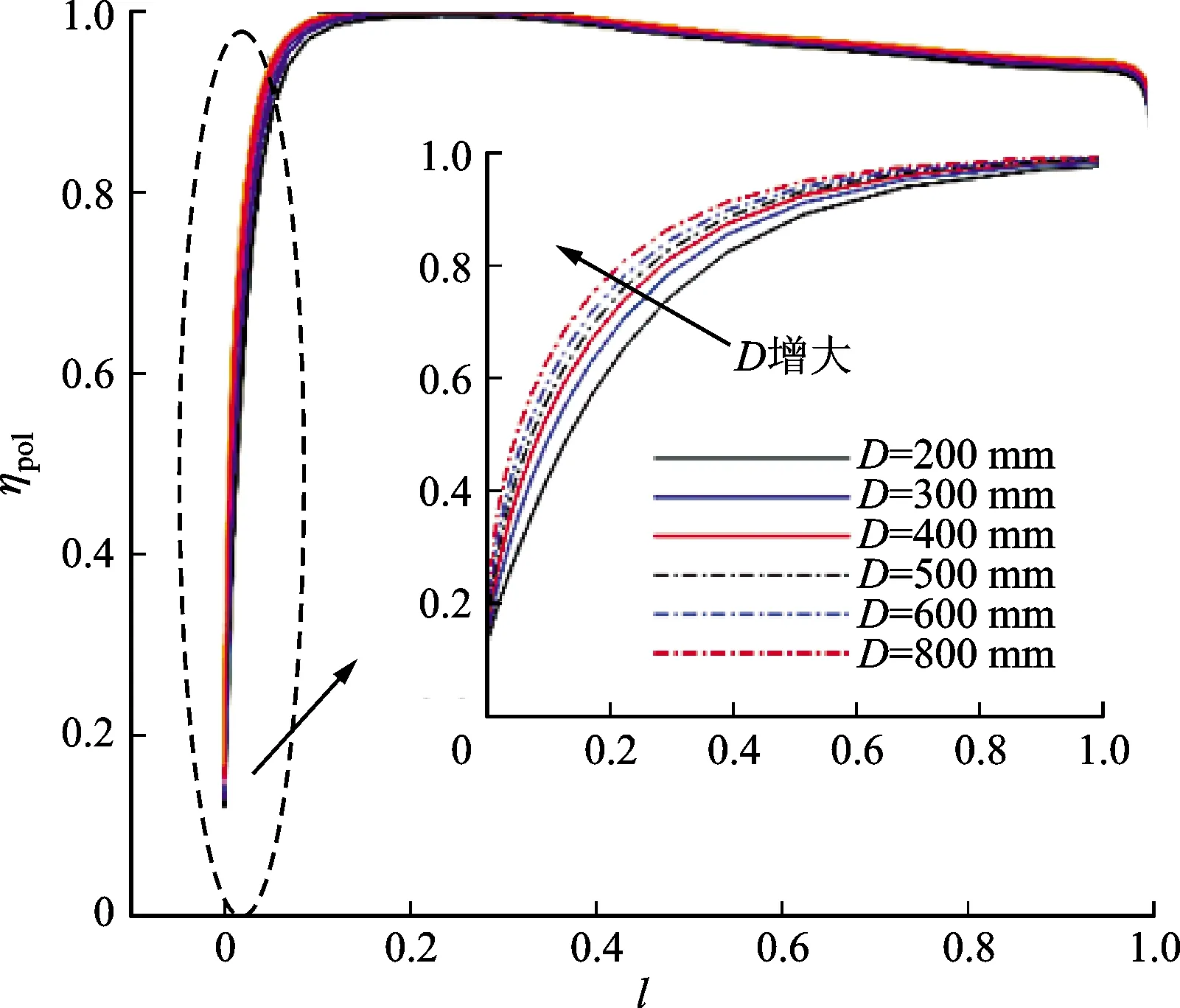
(c)多变效率图10 周向平均参数沿叶轮出口宽度的变化曲线Fig.10 Variation curves of circumferentially averaged parameters along the width of impeller outlet

通过以上数值计算得到不同流量系数φm及叶轮出口直径Dm的基准级效率ηm与对应的产品级效率η1,相应的基准级黏损比函数Xm可通过下式计算得出Xm的计算值如表2所示。

表2 Xm的计算值Table 3 Calculated values of Xm

(18)

将黏损比函数Xm=Xf(φm,Dm)拟合成二次多项式

Xm=a0+a1φm+a2Dm+a3φmDm+

a4(φm)2+a5(Dm)2

(19)

式(19)中各系数的拟合结果如表3所示,其中基准级直径Dm取国际单位制m。

2.2 粗糙度引起的性能尺寸效应

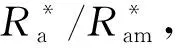
表4 θ2计算值Table 4 Calculated values of θ2

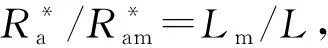
(20)

3 修正方程的验证

3.1 效率修正方程的验证

联立式(3)(10)(20)即得到本文提出的在离心压缩机模化设计中由雷诺数与粗糙度共同引起的效率修正方程

(21)

式中:ηm为基准级效率;L/Lm为模化比;Xm为基准级黏损比函数,具体形式见式(19);η为修正后的产品级效率。

表5给出了效率修正方程预测结果与实验值的对比,具体实验数据为:某高效点流量系数为0.068的模型级A由D=0.85 m模化至D=0.45 m时,其高效点多变效率由0.828偏移至0.809;某高效点流量系数为0.15的模型级B由D=0.4 m模化至D=0.8 m时,其高效点多变效率由0.802偏移至0.819。定义效率偏移量为产品级效率与基准级效率之差(Δη=η-ηm),可以看出,针对模型级A与模型级B,效率修正方程所预测出的产品级效率值与实测的产品级效率值之间的相对偏差在0.2%以内,所预测出的效率偏移量与实测的效率偏移量之间的相对偏差(定义相对偏差为预测值与实测值之差除以实测值)在9%以内,具有较好的修正效果。

表5 效率修正方程预测值与实测值的对比Table 5 A comparison of predicted values from efficiency correction equation and measured values

3.2 流量系数修正方程的验证

前文(1.2节)经理论推导给出了流量系数修正方程式(17)。从图10a中看出离心级流道内边界层名义厚度约为水力直径的5%左右,即δm～0.05dm。本文研究的离心级叶轮出口直径范围为0.2 m

(22)

(23)

上式说明,在离心压缩机模化设计中,粗糙度引起的流量系数偏移远小于雷诺数(边界层)的影响,因此略去小量(粗糙度Ra项)后,可得到忽略粗糙度影响时的流量系数修正方程为

(24)

由于离心压缩机的性能曲线在高效点附近相当平缓,且模化设计中流量系数的偏移幅度非常小,流量系数偏移量的精确测量十分困难,因此,本研究尚缺乏相关的实验数据。由CFD计算可以相对方便地获得高效点流量系数的偏移量,为此,本文利用CFD计算结果对流量系数修正方程进行验证。图11给出了由修正方程(24)得到的流量系数预测值(偏移预测曲线)与CFD计算结果的对比,图中实验点为CFD计算结果,曲线为修正方程预测结果,L/Lm=1时为基准级。数值计算结果为分别以D=200 mm的1号和2号模型级为基准级,模化至D=300,500,800 mm时的高效点流量系数φh。由图11可得:流量系数修正方程的预测结果与数值计算结果基本吻合,在0.25～4.0模化比范围内预测出产品级高效点流量系数与实测值之间相对偏差在1%以内。

图11 流量系数预测值与计算值比较Fig.11 A comparison of predicted values of discharge coefficient and calculated values

4 结 论

本文以离心级为研究对象,通过理论分析提出了一种新的效率偏移效应修正模型;同时引入边界层的影响,进一步发展了流道收缩效应模型对流量系数进行修正。由理论及数值模拟研究,给出了离心压缩机模化设计中的尺寸效应修正方程,并得出:模化设计中离心压缩机效率的偏移主要由雷诺数及粗糙度两方面因素引起;而流量系数(通流能力)的偏移则主要由雷诺数引起,粗糙度的影响可以忽略。通过与实验测试结果比较,经本文提出的效率修正方程预测出产品级效率与实测值之间的相对偏差在0.2%以内,预测出效率偏移量与实测值之间的相对偏差在9%以内,具有较好的修正效果。经理论推导获得的流量系数修正方程能在较宽模化比范围内预测流量系数偏移,其预测结果与通过CFD计算获得的结果较为一致,在0.25～4.0模化比范围内预测出产品级高效点流量系数与实测值之间相对偏差在1%以内。本文提出的以上2个修正方程的推荐应用范围为0.25

致谢:诚挚感谢沈阳鼓风机集团研究院副总工程师孙玉莹为本研究提供了D=500 mm的1号模型级实验性能曲线,以及模型级A、模型级B模化前后的性能实验数据。