带落角约束的中远程地空导弹高抛弹道优化设计∗
2021-10-11陆巍巍代进进唐嘉钰杜海东
陆巍巍 代进进 唐嘉钰 张 鑫 杜海东
(1.海军航空大学 烟台 264001)(2.91614部队 大连 116044)(3.92497部队 陵水 572425)
1 引言
无论是倾斜发射,还是垂直发射,地空导弹采用“高抛”飞行弹道,可以在导弹外形尺寸和重(质)量一定的情况下,通过提高导弹的飞行高度,在大气密度较小的高空飞行一段时间,以节约能量消耗,可以大大提高地空导弹的射程[1~2]。对于中远程地空导弹来说,最优的飞行弹道应该是“高拋”弹道。地空导弹飞行过程中,其固体发动机工作时间一般10s~20s,因此,大部分飞行时间内地空导弹处于被动飞行段,即依靠惯性飞行。当发动机停止工作后,地空导弹采用“高拋弹道”,从高空向低空飞行,将势能转化为动能,从而使地空导弹保持较高的平均飞行速度,直到命中目标为止[3~4]。
现代空袭作战中,超低空突防已成为空袭目标的一种主要战术手段。受地海杂波的影响,中远程地空导弹雷达导引头对超低空目标的测量精度会下降,若不对视线角进行约束,将导致制导精度严重恶化。研究表明,当视线角在布鲁斯特角附近时,地海杂波反射系数最小,导引头测量精度较高[5]。因此,在中远程地空导弹的弹道设计中应考虑弹道的末端视线角约束。
本文将综合考虑高抛特性和末端约束特性对中远程地空导弹的飞行弹道进行优化设计。
2 高抛弹道设计模型
中远程地空导弹,由于导弹飞行时间较长,不同飞行阶段导引信息获取方式也不同,从而中远程空空导弹一般采用“初制导+中制导+末制导”三阶段制导的复合制导方式。初制导主要依靠地空导弹武器系统对目标探测解算预测命中点信息,对导弹进行控制参数装订,采取程序指令控制实现;中制导依赖地空导弹自身的惯导设备+地面制导设备的修正指令完成飞行;末制导主要是依靠地空导弹导引头捕获目标而进行主动寻的飞行[6]。中制导是导弹制导过程中控制时间最长的且对导弹射程影响最大的阶段。一般来说,中制导在设计时要充分衡量能量耗散的问题,尽量减小能量的消耗,使导弹在中制导过程中达到尽量远距离并且在结束时能供给末制导尽量大的初始能量[7]。因此,本文重点讨论中远程地空导弹中制导弹道的优化设计。
经过大量的分析研究和多种途径的比较,飞行弹道选择四次方程曲线:y=Ax4+Bx3+Cx2+Dx+E,这种弹道与弹道式弹道比较接近,其能量消耗是最节约的,四次方程中系数通过优化设计计算确定[8]。
2.1 选取坐标系
地空导弹弹道设计一般按照纵向平面和侧向平面分别设计,高抛弹道的设计仅针对纵向平面。
如图1所示,高抛弹道的起点为O点和终点(遭遇点)为E点。建立以下两种坐标系。
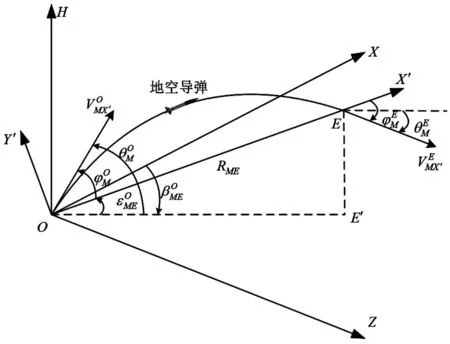
图1 中远程地空导弹高抛弹道示意图
1)地面参量坐标系OXHZ:取弹道起点O为坐标原点,OX轴指向平行目标速度矢量在水平面投影,方向相反,OH轴垂直于水平面向上,OZ轴由右手定则确定。
2)基准坐标系 OX′Y′Z′,取弹道起点 O 为坐标原点,OX′轴从起点指向遭遇点E,OY′轴垂直于OX′轴向上,OZ′轴由右手定则确定。


2.2 模型建立


3 参数优化
3.1 目标函数

3.2 约束条件
通常高抛弹道有两种形式:一是对应于最大飞行距离和最大飞行高度[9];二是对应于最大飞行距离和最小飞行高度,这里采用前者对高抛弹道进行约束。
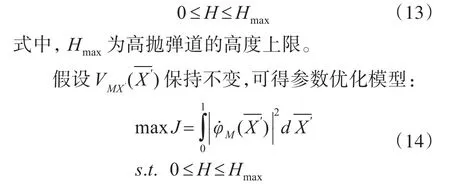
4 弹道滚动优化流程
某在中制导阶段,地空导弹高抛弹道的解算是循环进行的,弹道起点是地空导弹解算时刻的坐标点,终点是当前态势条件下地空导弹与目标的遭遇点[10~11]。在地空导弹飞向目标过程中,目标不可避免地要进行机动飞行,遭遇点和相应的高抛弹道也随之不断地变化。为了避免这种变化引起地空导弹的频繁机动飞行,只要与目标的遭遇点的变化不超出一定范围,地空导弹的飞行方向将不作或仅作小的调整,对于引起的误差,将在末制导飞行段由末制导律来消除[12]。弹道滚动优化流程如图2所示。
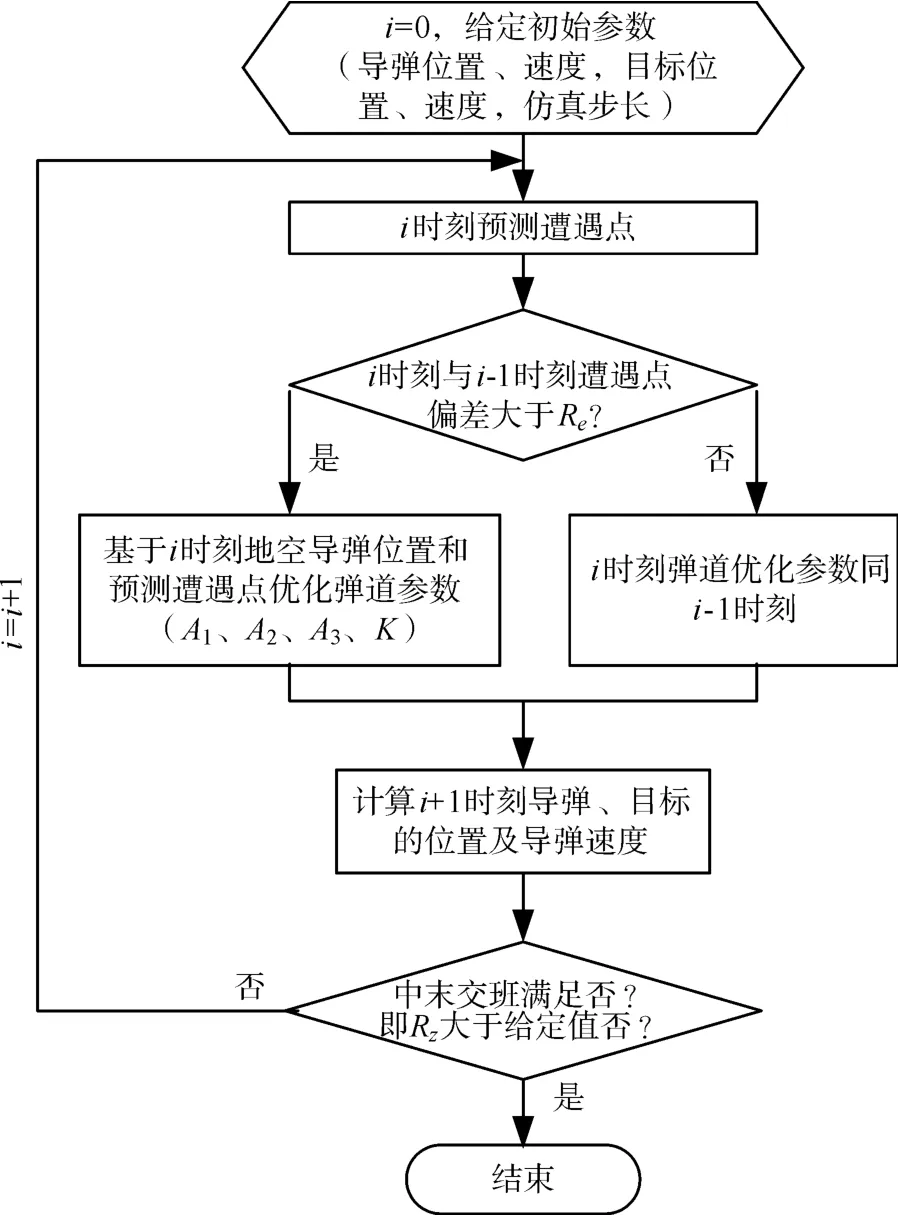
图2 弹道滚动优化流程
使用i时刻遭遇时间:
OXHZ坐标系下,i时刻导弹位置为(XMi,HMi,ZMi),导弹速度为(VxMi,VhMi,VzMi),i时刻目标位置为 (XTi,HTi,ZTi),目标速度为(VxTi,VhTi,VzTi),则i时刻遭遇时间为
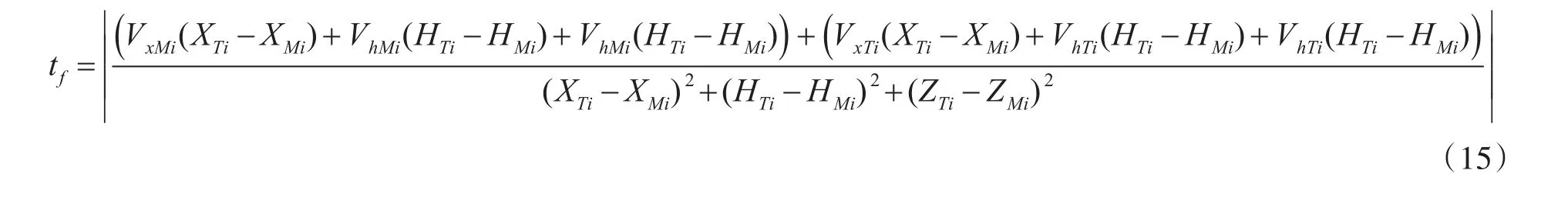
i时刻遭遇点坐标:

5 仿真验证
5.1 初始参数
地面参量坐标系OXHZ下导弹初始位置即弹道起点O 为(0,0,0),导弹初始弹道倾角=60°,导弹位遭遇点时弹道倾角=-10°,导弹飞行速初始度vm=1000m/s。
目标飞行速度vT=300m/s,速度倾角=-180°,目标位置 T 为(96000m,500m,0),根据遭遇点计算公式可得初始时刻弹目遭遇点E为(60000m,500m,0)。
高抛弹道的高度上限Hmax=30000m,i时刻与i-1时刻预测遭遇点调整的最小距离偏差为Re=1000m,末制导开机距离Rzd=8000m。
5.2 仿真结果
弹道归一化系数:A1=0.1849,A2=1,A3=0.5142,K=-0.0418,即高拋弹道归一化形式为
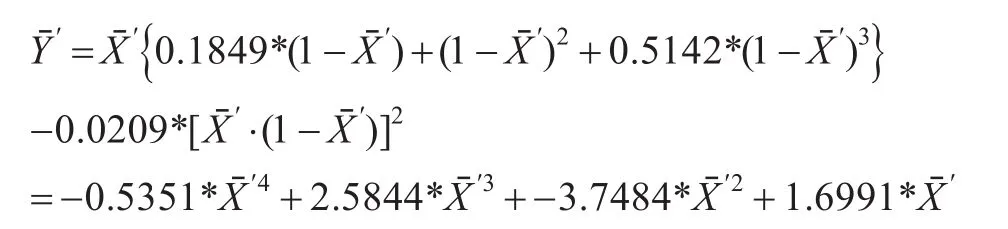
高抛弹道仿真结果如图3所示。
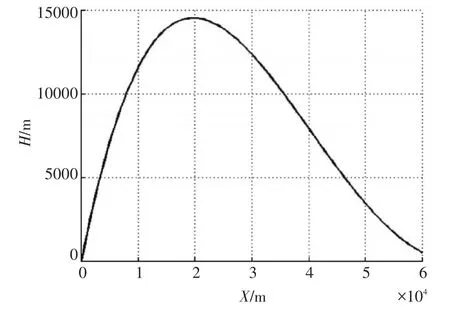
图3 高抛弹道示意图
导弹弹道倾角仿真结果如图4所示。
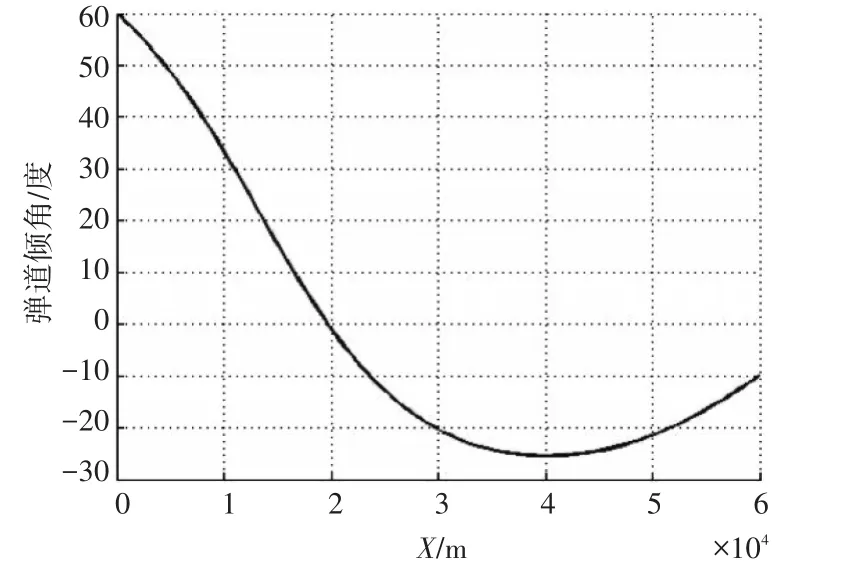
图4 弹道倾角变化示意图
6 结语
本文选取四次多项式方程作为高抛弹道设计模型,以能量效率最优为目标,在末端落角和高度限制约束下,建立高抛弹道优化设计模型,采用滚动优化求解方法对弹道优化模型的弹道系数进行求解。仿真结果表明,该弹道优化设计方法能有效解决高抛弹道的优化设计问题。
