改进遗传算法在计算机数学建模中的应用研究

2021-10-10张琳娜

电子设计工程 2021年19期

张琳娜

（陕西国防工业职业技术学院，陕西西安 710302）

遗传算法的基础思想就是对生物界遗传过程的模仿，整个过程通过3 个基本操作构成，分别为选择、交叉和变异，用染色体表示二进制，用基因表示参数，最后得到群体。在层数较多时，基本遗传算法存在编码冗长和寻优效果差的问题。所以，为了解决基本遗传算法的问题，通过深入研究与分析，提出改进遗传算法。该算法的遗传编码操作简便，方便交叉与操作，提高了操作的便捷性与简单性，还能够减小矩阵编码长度，在理论与实践方面有一定的突破与创新[1-2]。

1 遗传算法的设计

1.1 遗传算法设计步骤

在使用遗传算法求解问题时，首先要设计并改进算法，其步骤为：

1）确定编码方案。遗传算法利用编码的解决方案进行求解；

2）确定适应度函数。适应度值能够度量解的好坏，大部分都是基于目标函数来表示；

3）确定选择函数。使用优胜劣汰选择机制，提高高适应度值个体的存活概率；

4）选择控制参数。包括算法执行最大迭代代数、种群规模、不同遗传操作执行概率；

5)设计遗传算子。包括选择、交叉和变异；

6)确定算法终止规则；

7）编程上机运行。根据遗传算法结构编程，得到问题求解[3]。

1.2 编码方法

如何使用编码方案完善具体应用问题，是遗传算法主要研究方向，一般都是利用两条操作性较强的编码原则进行参考[4]。

1）二进制编码。二进制编码利用符号集{0,1}，其创建个体基因型为二进制符号串，长度和问题解精度具有密切关系。假如某参数取值范围为[Vmin，Vmax]，利用二进制编码符号串对此参数表示，其能够产生2i种不同基因个体，关系为式（1）：

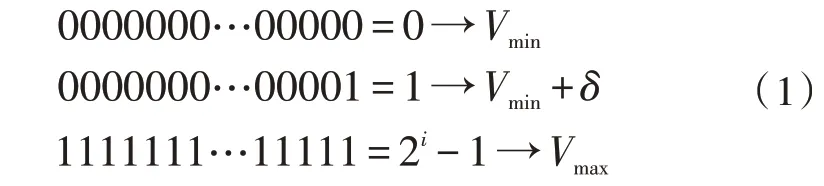
该方案精度表示为式（2）：

假设某个体编码表示为：X:bi,bi-1,…b1，解码公式表示为式（3）：

二进制编码方案主要优势为编解码操作较简单，方便实现交叉等遗传算法，直观且易懂[5]。

2）浮点数编码。浮点数编码方法对浮点运算使用的范围进行定义，表示个体长度与决策变量，代表基因个体价值。因为此编码方法为决策变量真正的价值，所以浮点编码也是真正价值编码方法。比如，某优化问题具有4 个设计变量xi，变量都具有与其相对的上下限，那么得到式（4）：

相应的表现形式为式（5）：

与其他编码相比，此编码能够应用到高遗传算法精确度范围中，使运算效率得到提高[6]。

1.3 基本遗传算子

遗传算法是将搜索算法与自然选择算法作为基础，是一种基于自然选择与遗传机理的随机搜索方法，主要包括变异算子、交叉算子、选择算子。通过交叉算子与选择算子实现遗传算法的搜索功能，接近最优解能力。

1）选择算子。选择指的是通过群体对优良个体进行选择，淘汰劣质个体，其能够使目前群体中的个体根据适应度值成为新群体中的幅值[7]，具体过程为：

假设第t代种群A(t)个体数指的是m，也就是m(H,t)。在对操作进行选择的过程中，位串Aj通过概率被选中并且复制，fi指的是个体Aj(t)的适应度。假设一代中群体大小为n，而且个体两两不相同，那么模式H在第t+1 代中样本数表示为式（6）：

公式中的f(H)指的是t时刻所对应平均适应度值，假设群体平均适应度值表示为式（7）：

假设模式H平均适应度比群体适应度要高，高出部分表示为cfˉ，c指的是常数，那么得到式（8）：

2）随机竞争选择。随机竞争选择根据轮盘赌选择个体时，利用个体竞争选中高适应度值的个体，进入到下一代个体中，淘汰低适应度值的个体[8]。

2 遗传算法的改进

2.1 自适应改进遗传算法运算流程

交叉算子能够通过基因重组得出优良个体，假如群体所有个体没有基因，通过交叉算法无法得出缺失基因，但是可以利用遗传算法得到。变异算子是指生物界基因突变的模拟，寻找群体个体缺乏的优质基因，对新个体进行计算。文中提出改进的自适应遗传算法[9]，执行流程为：

1）实现初始群体编码，并且设置收敛条件、种群大小、染色体长度；

2）全面计算个体的适应度值；

3）判断收敛条件是否满足需求，如果满足，就输入结果；如果不满足，就进入到下一步；

4）判断arcsin(fave/fmax)≥π/6 是否成立，成立则说明种群最大适应度和适应度平均值比π/6 要大，此时判断适应度值的集中度比较简单。这时对交叉和变异进行判断，有效执行选择操作；如果不成立，则说明种群适应度平均值不接近最大适应度，此时具有较大的种群差异度值。

5）回到第2）步[10]。图1 为改进算法的求解流程。

图1 改进算法的求解流程

2.2 改进算法的交叉概率与变异概率

为了能够充分发挥交叉概率Pc与变异概率Pm的适应度的集中分散程度，提出两者自适应选取计算公式：

当arcsin(fave/fmax)＜π/6 时，说明种群适应度平均值和最大适应度值并不接近，小于π/6 时能够判断此时种群适应度值分散，这时的种群差异较大、种类丰富，具有良好的多样性。提高交叉概率Pc值，交换染色体基因，进化优质新个体，降低变异概率Pm值和优良个体破坏的可能性，促进收敛的速度[11]。

另外，当arcsin(fave/fmax)≥π/6 时，表示种群适应度平均值接近最大适应度值，超过π/6 时要判断种群适应度较集中，缩小了种群差异度，缺乏丰富种群和优质个体，还会占据大量的算法执行时间。这时降低交叉概率Pc值和交叉操作，提高变异概率Pm值，避免陷入到局部极值，搜索全局最优解[12]。

2.3 最优保存策略

在实际使用的过程中，自适应遗传算法变异概率与交叉概率会在某个时刻变大，使良好优质体系遭到破坏。所以，文中利用最优保存策略对遗传每代最优个体进行保留[13]。对遗传操作后每代产生的全新群体和前一代群体中的最高适应值进行全面对比，假如比前一代最高适应值要小，就要将新一代个体淘汰，增加前一代高适应值。最优保存策略能够破坏最优个体遗传操作，这是文中自适应算法收敛性改进的基础[14]。

3 案例分析

文中遗传算法在改进之后具有较强的能力，能够避免传统遗传算法在辨识问题的复杂计算方法，辨识初始模型公式（10）为：

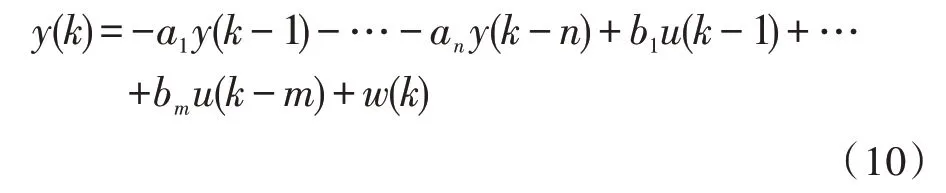
此辨识初始模型根据最小二乘法求出上述公式参数a1、a2b1、b2，为常见辨识方法。然后基于矩阵编码改进遗传算法，具体优化流程为：

1）根据待求参数个体确定矩阵串的列和行，假如有6 个待定参数，那么要确定3×2 或者2×3 个矩阵，此特定6 个参数利用6 个元素表示[15]；

2）在搜索参数过程中要确定其范围，遗传算法在搜索范围对参数存在相应极限，此范围是以具体问题进行确定；

3）合理评价个体适应度，文中根据最小二乘定义实现选择和评价。选择平方值平均最小一个组成为最优值输出，此为矩阵编码遗传算法与辨识度最小二乘两相结合的重点，在此过程中，矩阵编码结合最小二乘法，然后得到矩阵编码遗传算法搜索关键点。最后对比参数值与实际测量参数值差额取平方数，使其成为遗传算法适应度函数[16]；

4）为了避免优秀父串在交叉与变异过程中出现破坏，工作人员会使两个最优子代避免变异或者交叉，而是直接选择其子代。以下公式为Pc、Pm的说明：

4 实验结果

在此实践过程中，三阶线性离散系统输入输出数据一共40 个，最后以矩阵编码遗传算法最小二乘法实现参数估计工作[17]，在此试验计算过程中给定初始条件为公式（11）：

通过以上公式表示，y(k)为实际测量值，J(k)指的是矩阵编码遗传算法的最优参数[1.756 4 0.942 3 0.151 8 0.999 8 0.521 7 0.069 5]，但是在解码前要确定参数变化范围[18]，辨识结果表示为V=1.698 7 0.932 1 0.149 9 1.00 2 0.521 5 0.693。