某抽水蓄能电站引水调压室底部大直径三梁钢岔管优化研究

2021-10-10姚敏杰汪剑国李高会王颂翔

大坝与安全 2021年3期

姚敏杰，汪剑国，李高会，王颂翔

（中国电建集团华东勘测设计研究院有限公司，浙江杭州，311122）

水电站钢岔管主要结构型式有三梁岔管、月牙肋岔管、球形岔管、无梁岔管及贴边岔管五种，其布置形式有对称Y形、非对称Y形、三岔形等[1]。钢岔管通常应用于水电站机组前主管与支管连接部位，起到分散水流、连接不同发电机组的作用，其主管与支管轴线多位于同一水平面内。但在水电站工程的某些特定部位，有时也会根据需要设置一些特殊形式的钢岔管。例如在水电站调压室底部与输水道连接部位，当地质条件不适合布置混凝土衬砌时，钢岔管则成了连接输水道主管与调压室竖井连接管的必然选择。目前针对这类钢岔管研究较少。

结合某抽水蓄能电站实际工程情况，对其引水调压室底部设置的大直径钢岔管结构进行研究分析，通过运用ANSYS 数值分析软件进行三维有限元计算，最终得出合理的设计体型。

1 工程概况

某抽水蓄能电站枢纽工程地质条件复杂，主要表现在地质构造发育、岩层复杂、岩溶发育等，为解决输水系统沿线渗漏问题，引水隧洞全线（含上平段）采用全钢衬布置，在上平洞末端设置引水调压室。调压室型式为阻抗式，大井直径18.0 m，阻抗孔直径4.5 m，阻抗孔小井内套钢管与上平洞钢管呈90°垂直连接。因此，必须在该部位设置钢岔管，其中主管（调压室上游侧钢管）直径8.5 m；一支管（阻抗孔连接管）直径4.5 m，与主管夹角为90°，与主管采用锥形渐变连接；另一支管（调压室下游侧钢管）直径8.5 m，与主管在同一轴线上。

该钢岔管与常规钢岔管相比具有以下几个显著特点：（1）直径大，主管直径8.5 m，支管直径4.5 m，在同规模抽蓄中位于前列；（2）分岔角大，一支管（阻抗孔连接管）与主管垂直连接，分岔角达90°，结构受力不利；（3）地质条件差，隧洞沿线岩溶发育，围岩抗力不均。

2 有限元计算模型

2.1 岔管设计体型

钢岔管采用三梁岔管设计，三梁岔管可利用U梁和腰梁作为加强构件，共同起到加固管壁和承受外荷载的作用[2]。钢岔管体型示意见图1，包含引水上平洞主管、阻抗孔连接管支管、两U 梁以及腰梁。其中主管内径为8.5 m，阻抗孔连接管支管内径为4.5 m，岔管部位最大内水压力为0.89 MPa。通过公式估算和工程类比，并考虑该部位岔管的制造加工难度，岔管管壁厚度取30 mm。

图1 引水调压室底部三梁岔管体型（单位：mm）Fig.1 The three-girders reinforced branch pipe at the bottom of surge chamber(unit:mm)

2.2 有限元模型建立

根据岔管的体型参数，在大型通用有限元软件ANSYS 中建立了有限元模型，模型包括主、支管管壳及加强梁。由于管壳及加强梁厚度较薄，属于板壳薄壁结构，模型均采用四节点壳单元SHELL63。有限元模型在主、支管端部取固端全约束，为了减小固端约束对岔管的局部应力影响，主、支管段轴线长度取最大公切球直径的1.5 倍以上[3]。钢岔管计算模型网格离散见图2～3。考虑到岔管部位围岩地质条件差，引水调压室底部三梁钢岔管按明管设计，即不考虑围岩的分担作用，按钢管单独承担水荷载进行计算。

图2 三梁岔管整体计算模型网格划分Fig.2 Mesh of the whole model of three-girders reinforced branch pipe

2.3 钢岔管优化方案拟定

三梁岔管主、支管直径及管壳厚度一定的前提下，影响三梁岔管结构受力状态的主要是加强梁的设计参数，包含：加强梁厚度、U梁和腰梁外露高度以及U梁内伸高度[4]。为分析加强梁各设计参数对岔管结构受力的影响，得到最优设计体型，拟定以下计算方案进行有限元计算分析。各计算方案及相关参数如表1所示。

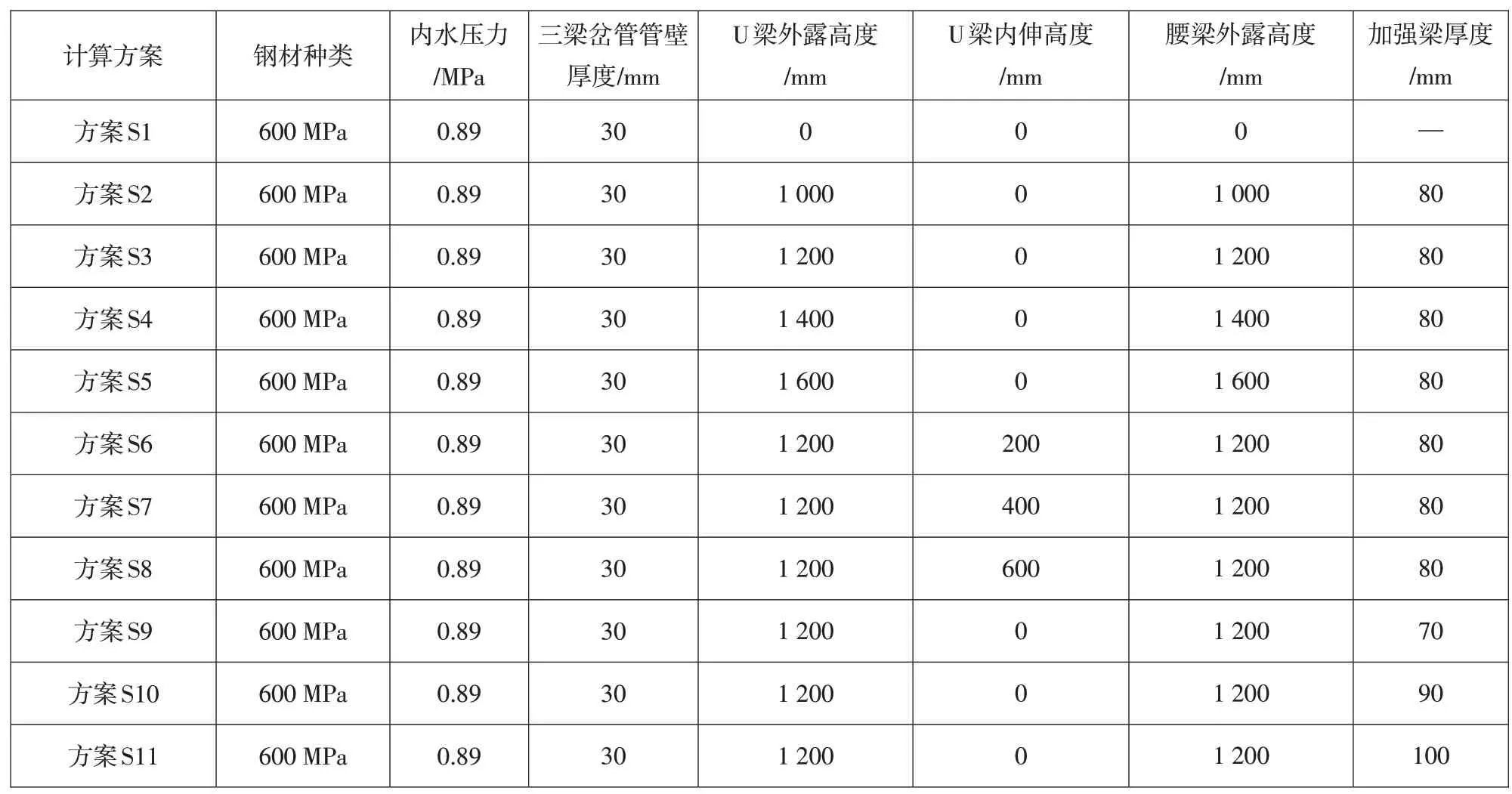
表1 三梁岔管计算方案及相关参数Table 1 Calculation schemes and parameters of three-girders reinforced branch pipe

为了减小岔管管壳及加强梁尺寸，三梁岔管管壳和加强梁均采用600 MPa 级高强钢。钢材容重γs=7.85×10-5N/mm3，弹性模量Es=2.06×105MPa，泊松比vs=0.30，相应的抗力限值按照规范NB/T 35056-2015[1]《水电站压力钢管设计规范》确定，具体数值详见表2。

表2 钢材抗力限值Table 2 Allowable stress of steel

图3 三梁岔管加强梁网格划分Fig.3 Mesh of reinforced girders

3 计算结果与分析

3.1 计算结果

对表1 中S1～S11计算方案分别建立有限元模型并提取有限元计算结果，得到各方案下岔管管壁及加强梁的位移、Mises应力，计算结果见表3～4。

表3 各计算方案管壳和加强梁最大位移（单位：mm）Table 3 The maximum displacement of the branch pipe and reinforced girders in different schemes(unit:mm)

表4 各计算方案管壳和加强梁最大Mises应力值（单位：MPa）Table 4 The maximum Mises stress of the branch pipe and reinforced girders in different schemes(unit:MPa)

方案S1 不设加强梁，此时岔管最大位移达115.5 mm，管壳表面峰值应力达1 335.3 MPa，远远超出局部膜应力+弯曲应力的抗力限值308 MPa。在设置加强梁后，岔管最大位移和应力值明显下降，说明加强梁作为岔管加强构件，对加固管壁、改善岔管受力有明显作用。

3.2 加强梁设计参数敏感性分析

3.2.1 加强梁外露高度敏感性分析

对比计算方案S2～S5，得到加强梁外露高度对岔管整体最大位移和应力的影响如图4 所示。由图4 可以看出，在加强梁厚度（80 mm）和管壳厚度（30 mm）相同，加强梁都不内伸的情况下，增加加强梁外露高度，管壳和加强梁最大位移基本呈线性减小的趋势；分布于管壳部位的整体膜应力、局部膜应力、局部膜应力+弯曲应力以及加强梁应力均有所减小，但整体膜应力变化很小，且各方案下整体膜应力均小于相应的抗力限值，不成为控制的应力种类。控制应力主要是局部膜应力+弯曲应力以及加强梁应力，加强梁外露高度达1 600 mm时，管壳和加强梁最大应力同时满足相应的抗力限制要求。同时可以看到，在梁外露高度增加至1 400 mm后，局部膜应力+弯曲应力几乎没变化，说明仅靠增大加强梁外露高度，对改善岔管管壳应力分布效果较为有限。

3.2.2 加强梁内伸高度

加强梁不内伸情况下，外露高度需达1 600 mm，管壳和加强梁最大应力才能同时满足相应的抗力限制要求，且此时管壳局部膜应力+弯曲应力达到307.8 MPa，距离抗力限值308 MPa裕度很小。考虑到加强梁外伸高度太大时需增大开挖体型和回填混凝土量，对施工便利及经济合理性不利，选择对U 梁1 和U 梁2 进行内伸，各加强梁外露高度保持1 200 mm 不变。对比计算方案S2 与S6～S8，得到加强梁外露高度不变时，U梁内伸高度对岔管整体最大位移和应力的影响，见图5。由图5 可以看出，在加强梁厚度（80 mm）和管壳厚度（30 mm）相同、且加强梁外露高度1 200 mm 不变的情况下，增加U 梁1 与U 梁2 的内伸高度，管壳和加强梁的最大位移、应力减小均较为明显。对比图5 与图4 的变化趋势，说明增大U梁内伸高度比增大外露高度对改善岔管整体应力分布更明显，各加强梁外露高度保持1 200 mm不变时，U梁内伸400 mm，管壳和加强梁最大应力同时满足相应的抗力限制要求，且此时都留有一定的安全裕度。

图4 加强梁不同外露高度岔管最大位移和应力曲线Fig.4 The maximum displacement and the stress of branch pipe with different exposure height of reinforced girders

图5 加强梁不同内伸高度岔管最大位移和应力曲线Fig.5 The maximum displacement and the stress of branch pipe with different internal extension height of reinforced girders

3.2.3 加强梁厚度

加强梁厚度直接影响加强梁的整体刚度和应力分布，对比计算方案S2与S9～S11，得到加强梁厚度对岔管整体最大位移和应力的影响如图6 所示。由图6 可以看出，在加强梁外露1 200 mm、不内伸且管壳厚度（30 mm）相同的情况下，增大岔管加强梁壁厚，管壳和加强梁的最大位移、应力均呈减小趋势，但可以看到，加强梁厚度由90 mm 增至100 mm时，分布于管壳部位的局部膜应力+弯曲应力基本没变化。加强梁厚度需增至100 mm，管壳和加强梁最大应力才能同时满足相应的抗力限值要求。考虑加强梁厚度增加不仅不经济，还会增加焊接安装的施工难度，故加强梁厚度采用80 mm。

图6 加强梁不同厚度岔管最大位移和应力曲线Fig.6 The maximum displacement and the stress of branch pipe with different thickness of reinforced girders

3.3 推荐方案

通过对加强梁外露高度、内伸高度、厚度这三个关键设计参数对岔管整体受力影响的敏感性进行分析，得出增大这三个设计参数值均能一定程度改善岔管管壳和加强梁的应力分布。其中增加U 梁内伸高度对改善控制性管壳部位的局部膜应力+弯曲应力，加强梁本身应力大小效果尤为明显，且更为经济合理。综合以上分析，采用方案S7 作为岔管的推荐设计体型，即加强梁外露高度1 200 mm、U 梁内伸高度400 mm、加强梁厚度80 mm，该方案下岔管管壁及加强梁的位移、Mises应力分布见图7。

图7 方案S7三梁岔管位移、应力分布图Fig.7 The displacement and stress distribution of branch pipe in scheme 7

从变形来看，受加强梁的约束作用，钢岔管沿主管水平两侧向外膨胀，在U梁及腰梁相交部位的主管中部位移比较大，其中岔管管壁最大位移为12.8 mm，加强梁最大位移为7.5 mm。从应力来看，钢岔管管壁中面的较大Mises应力出现在主管与锥管、锥管与支管交界处，但最大值155.0 MPa 远小于相应的局部膜应力抗力限值261 MPa；钢岔管管壁表面Mises 应力最大值出现在主管与锥管交界处，数值大小为292.7 MPa，小于相应的抗力限值308 MPa；加强梁Mises应力最大值出现在U梁内侧中部，数值大小为238.3 MPa，小于相应的抗力限值261 MPa。