植被根吸水对植被斑图的影响研究∗
2021-10-10阿卜杜许库尔热合曼阿布都热西提阿布都外力
阿卜杜许库尔·热合曼,阿布都热西提·阿布都外力
(新疆大学 数学与系统科学学院,新疆 乌鲁木齐 830046)
0 引言
干旱-半干旱的生态系统覆盖了地球约40% 的陆地面积[1−2],沙漠化进程成为全世界面临的重要生态问题.此外,联合国可持续发展司表示,沙漠化和土壤水流失的加剧影响世界约25%的人口生存[3].了解植被斑图模式的产生机制是治理荒漠化的前提[4].因此,干旱-半干旱区植被斑图的形成是生态动力学家关注的重要课题之一.
众所周知,在不同的区域会观察到许多种不同的植被斑图模型[4],比如:点状分布的植被斑图、间隙状分布的植被斑图、斑纹状灌木丛植被斑图、环状草丛植被斑图、迷宫形分布的植被斑图以及带状分布的植被斑图[5−10].一般来讲,植被斑图模型的形成与水资源匮乏、植物对水的竞争、水扩散和流动的分布、牲畜的放牧、气候的变化、土地特征以及土壤中素有关[9,11−14].最近对干旱生态系统中植被斑图空间组织和植物与有限资源之间的正反效应方面已取得了很大的进展[15].Lefever 和Lejeune[16]建立的模型指出植被模式的形成仅取决于植物的特征.Klausmeier[6]构建的模型中,考虑了土壤水分动态,并指出植物增加局部水分利用率会更有利于它们的生长.Okayasu 和Riretkerk 等人[10,17]引入水平衡并分解为土壤水和地表水,指出这两个水资源与植被的不同相互作用.
了解植被斑图模型的产生机制以及对环境的适应能力是研究气候变化和过度放牧破坏自然平衡而导致的荒漠化的重要前提[18].Reinier 等人[19]提出了包括物种(灌木)、土壤水及地表水-植物系统:

其中:P 表示植物量或者密度(g/m2),W,O 分别表示土壤水量和地表水量或密度(mm);cgmaxP 是植物生长率;c 表示植物吸收水分转化为植物生长的过程(g/mm m2);gmax表示植物最大的土壤比吸水量(g m2/mm d);k1表示半饱和常数(mm);d 表示由于死亡率和放牧造成的植物密度的特定损失率(d−1);αO 表示地表水渗透率,αO 是描述地表水最大入渗率的术语;αOf0为无植物时的最小入渗量(如果P=0);α 表示可渗透的地表水比例(d−1);k2表示入渗饱和常数(g/m2);f0表示在没有植物的情况下最小的水分渗入量(无刚量);r 表示由于蒸发和排水造成的特定土壤水分损失(mm).R 表示降雨量(mm/d);D1,D2,D3分别表示植被密度扩散(m2/d),土壤水和地表水的扩散(m2/d).△表示拉普拉斯算子.

其中:D21的大小体现土壤水扩散反的强度,间接地反映了植被根部对土壤水的吸收能力.△(D2W −D21P)描述了植被对水的扩散的影响.反应方程g1,g2,g3可以写成如下形式:

本文先分析模型(2) 对应的常微分方程的常数解的稳定性,然后在常微分方程稳定性基础上分析偏微分系统的稳定性,并得到了植被斑图产生的参数条件,最后通过有限差分法验证了模型.
1 Turing 不稳定性
首先分析模型(2)对应的常微分方程

通过简单的计算,可以得到模型(3)有两个常数平衡点,分别是裸土平衡点E1和具有植物的平衡点E2.

由于f0<1(地表水渗入地下水的比例在P 中没有增加),可知α1,β,δ,ν,η 是正常数.
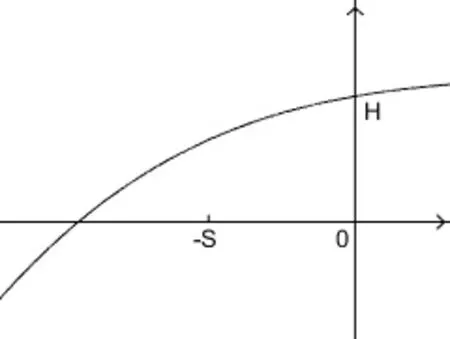
定理1(1) 如果 证明(1)求特征值det(λI −J(E1))=0 得 (2) 直接求平衡点E2特征值比较复杂,因此利用一元三次函数的性质和零点二分法确定平衡点E2的特征值即可.求特征方程N(λ)=det(λI −J(E2))得 其中:s=δ+ν,h=δα1β+α1δη,l=δν+α1β.显然s,l 和h 是正常数.N(0)=h,N(−s)=−sl+h.由h>0,至少存在一个负实根的零点. 假设N(−s)=−sl+h>0,相当于 则N(0)N(−s)>0,可知λ1∈(−∞,−s).由一元三次方程根的性质知 容易知道λ2,λ3具有正实部的根. 假设N(−s)=−sl+h<0,相当于 则N(0)N(−s)<0,λ1∈(−s,0).由一元三次方程根的性质知 λ2,λ3是负实根或者具有负实部的根. 在恒定平衡点E=(P∗,W∗,O∗)上,模型(2)的线性化系统可以写为 因此,线性化问题的稳定性取决于矩阵−µD+A 的特征值,其中 定理2如果那么模型(2)的平衡点E1是稳定的. 证明当E=E1时,求−µD+J(E1)的特征值.det(λI+µD−J(E1))=0,解得 注:裸土平衡点上常微分系统和偏微分系统都是线性稳定的,所以该平衡点上不产生植被斑图. 定理3假设d,模型(2)有一个正平衡点E2.并有以下结论: (1)(a)如果α1δη<δν(δ+ν)+να1β,D21 (b)如果α1δη<δν(δ+ν)+να1β,D21>min那么平衡点E2是不稳定的.这里分别表示: (2)当α1δη>δν(δ+ν)+να1β 时,那么平衡点E2是不稳定的. 证明和定理1中(2)的证明方法一样,直接求平衡点E2的特征值比较复杂,利用一元三次函数的性质和零点二分法确定平衡点E2的特征值即可.求平衡点E2的特征函数 S,L 和H 是实常数,其中的S>0. 先证(1).当H<0 时,存在一个正实数根(见图1).H<0 相当于 图1 H<0 Fig 1 H<0 当D21>时,有H<0,因此模型(2)是不稳定的. 当H>0 时,容易知道M(λ)存在一个实根λ1<0. (a)假设H>0,−SL+H>0,有λ1<−S (见图2).由λ1+λ2+λ3=−S,有 图2 −SL+H<0 Fig 2 −SL+H<0 因此至少存在一个正实部根.−SL+H>0 相当于 假设α1δη<δν(δ+ν)+να1β,定义 当D21>时,有H>SL. (b)假设H>0,−SL+H<0,得知L>0,有λ1>−S (见图3).可以将另外的两个根λ2,λ3的和的形式表示出来,即 图3 −SL+H>0Fig 3 −SL+H>0 因为S,L,H>0,M(0)=H>0,不存在正实根.因此λ2,λ3是负实根或者具有负实部的共轭复根.−SL+H<0 相当于 假设α1δη<δν(δ+ν)+να1β,当D21<时,有SL>H. 综合D21 (2)假设α1δη>δν(δ+ν)+να1β,µ=µ1=0 时,H>SL. 图灵不稳定性是指常数平衡点对于常微分方程是稳定的,但对于偏微分方程是不稳定的.因此模型(2) 带交叉扩散时会产生Turing 不稳定性[20]. 利用有限差分法[21]进行模型(2)的二维数值模拟,研究区域是干旱-半干旱地区,参考灌木类的植被做植物模型.由于条件有限,无法实地调查,因此本文选取文献[10]的参数值.模型(2)的参数值 下面随机取初始值P0=0,W0=5,O0=25,研究区间50×50 作为固定,取不同交叉扩散率D21,进行了数值模拟. 从图4 可知,D21的变化会影响植被的分布状态,深黄色表示植物密度高或者植物量多.由图4(a) 可知,D21很小时对模型的影响不大,由图4(b),图4(c) 可知,D21足够大时形成斑图形式.由图4(d)可知,D21比较高时,植物密度减少或者植物量较少.因此D21的大小会影响植被斑图的形成. 图4 干旱区内植被分布状态的二维模拟结果Fig 4 Two dimensional simulation results of vegetation distribution in arid area 本文主要研究了植被斑图的产生原理.利用偏微分方程的线性稳定性方法得到了产生Turing 斑图的条件.通过数值模拟可以知道,植物根部可以防止有限的水资源的流失.用数学语言来说,在水-植被动力系统中各个参数的影响下会出现图灵(不)稳定性.因此进一步研究半干旱-干旱区域植被斑图模型的形成机制,对防止土壤沙漠化具有重要的实际意义.




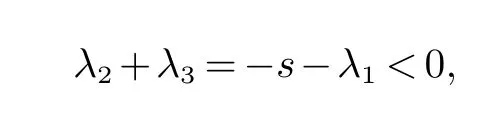

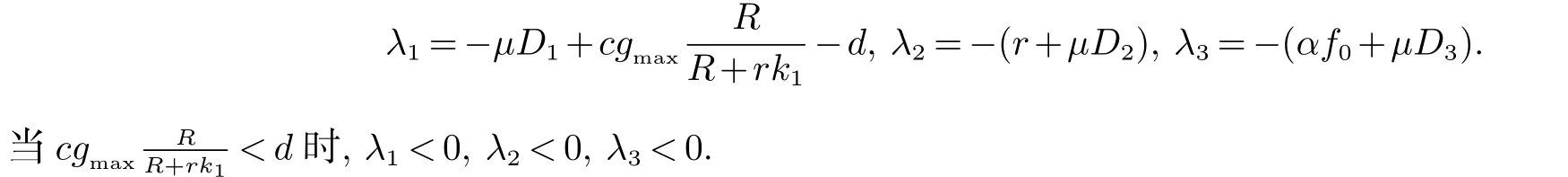
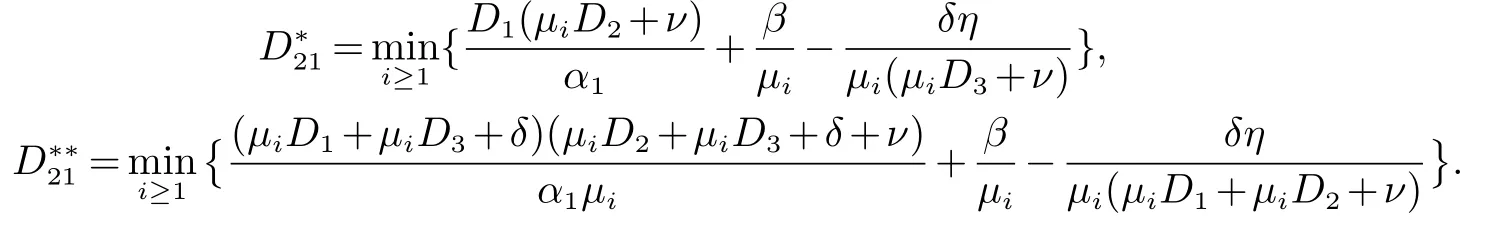
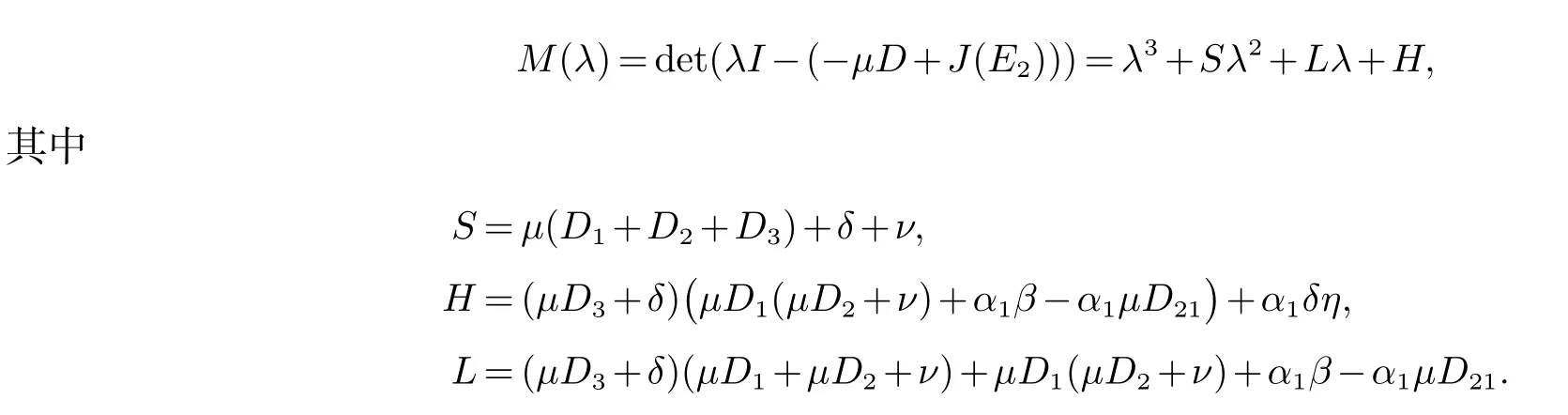


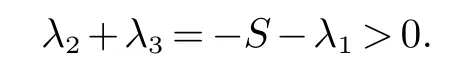





2 数值模拟
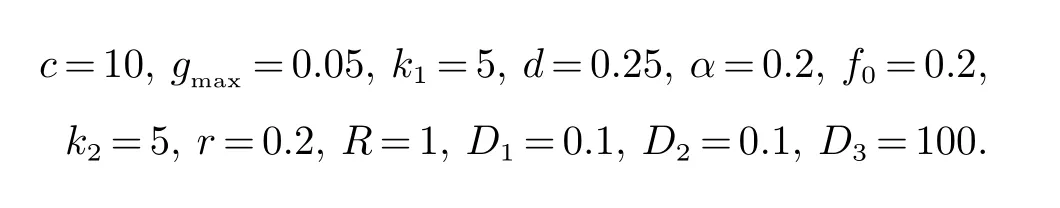

3 结 论
