基于GSO-BP的数控机床进给轴热误差补偿研究
2021-10-10张红欣
张红欣
(昌吉学院,新疆 昌吉 831100)
0 引 言
现代机械制造中,精密和超精密加工技术已成为制造强国的关注点,机床在加工过程中,各部件受到环境温度、切削过程、冷却液、电机等热源的影响而产生热变形[1]。大量研究显示[2],机床因受热而形成的热误差占机床总误差的40%~70%。因此,减小机床热误差对提高机床加工精度至关重要。若采用误差防止法(即利用设计和制造途径减少或消除可能的热误差源,或通过控制温度因素来满足加工精度要求)会形成昂贵的系统成本,不仅易受外界环境干扰引起误差,而且现有的加工能力将遭到限制。误差补偿法是采用某种控制策略,利用计算机技术和传感器技术,由执行机构对误差源进行分析、建立数学模型,快速计算补偿量,并反馈到控制系统中,实现驱动量的修正,最后实现减小加工误差的目的[3-4]。
为使被加工件可能获得比“母机”更高的加工精度,本文采用萤火虫优化算法优化BP神经网络,使得BP神经网络具有最优的网络初始值和阈值,通过传感器技术实时检测关键点温度,通过各进给轴热误差模型实时推断和预测热变形误差的情况,并将预测所得的热误差补偿量输出至PMC,可在一定程度上提高热误差补偿的精度,使得数控机床实时补偿更有效。
1 各进给轴补偿建模方法
1.1 萤火虫优化算法
萤火虫算法(Glowworm Swarm Optimization, GSO)是一种基于萤火虫群体随机搜索而形成聚集在少数位置现象的一种智能优化算法[5]。分布在目标函数定义区间内的每只人工萤火虫各自携带自身的萤光素,并拥有各自的活动区间,该区域称为决策范围。各萤火虫的亮度与各自所在位置的目标函数适应度值有关,越亮的萤火虫表示它成为目标值的可能性更大。GSO算法主要由初始化萤火虫信息、更新荧光素、更新萤火虫位置、更新决策域四阶段构成。
该算法模拟萤火虫通过个体发光来吸引同伴或猎物,从而实现绝大多数个体最终聚集在若干个具有较优目标函数值位置的目的。
假设目标群体中共有N只萤火虫,其中(xi, yi)表示第i只萤火虫所在的位置,对应目标函数为f(xi, yi),Ti为该处萤火虫荧光素的值,每只萤火虫的决策半径采用式(1)实现更新:

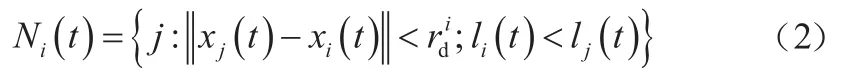
式中:||x||为x的范数;xj(t)为第j只萤火虫在第t代的位置;lj(t)为第j只萤火虫在第t代所具有的荧光素值。
第i只萤火虫向其邻域的萤火虫j移动的概率表示为Pij:

第i只萤火虫的位置更新公式为:
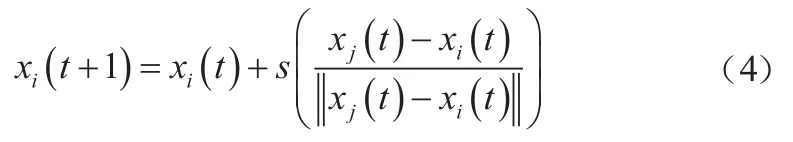
式中,s为萤火虫移动的步长。
第i只萤火虫的荧光素值的更新公式为:

式中:li(t)为第i只萤火虫经t次迭代后的荧光素值;ρ∈(0, 1),为荧光素所占的权重;γ为荧光素的更新频率;f(xi(t))为适应度函数值。
萤火虫算法在具体迭代运算中进行数据处理的流程如图1所示。

图1 萤火虫算法工作流程
1.2 BP神经网络
BP神经网络[6]应用广泛,具有非线性映射等特点,其学习过程由正向数据传播和反向误差传播组成。
数控机床各进给轴在运动过程中所需的补偿量应在较短时间内进行预测,本文考虑到原始BP神经网络算法在训练过程中收敛较慢,为满足控制系统的实时应用,结合共轭梯度学习算法对传统BP神经网络进行了改良。
通过解析BP算法的推演过程可知[7],原始算法利用梯度下降法实现逐步逼近,但该方法在具体仿真时所耗费的仿真时间较长,不能满足系统要求的实时性。因此本文在原有基础上加入了共轭梯度学习算法,这种方法可以在更少迭代次数的情况下达到收敛。它带来的额外代价是迭代计算的工作量有所增加。尽管如此,许多应用已表明,共轭梯度学习算法总的收敛速度相比常规BP算法提高了数十倍甚至更多。
共轭梯度学习算法原先应用于求解非线性多变量函数的极值,共轭梯度求解的计算流程如图2所示。

图2 共轭梯度学习算法求解过程
2 GSO-BP算法模型分析
2.1 模型建立基本思想
BP神经网络算法随着训练样本维数的不断增加,其收敛速度将变慢,网络性能降低,若网络的初始值和阈值选择不当,将导致网络难以收敛[8]。因此,通过萤火虫优化算法为改良后的BP神经网络提供最优的初始值和阈值,可使整个网络得到较为准确的预测值,为各进给轴提供较精确的补偿,从而实现在热因素环境下的误差补偿。
2.2 GSO-BP实现原理
对于神经网络而言,若把神经网络看成是一个预测函数,萤火虫算法优化网络中得到的最优预测值为BP神经网络提供最优初始权值和阈值,优化后网络的预测效果明显优于未优化的网络。网络经训练后输出的预测值更准确,系统实时性更强。将萤火虫算法与BP神经网络算法相结合进行运算的工作流程如图3所示。

图3 GSO-BP网络工作流程
2.3 GSO-BP算法仿真分析
GSO-BP神经网络有6个输入参数、1个输出参数,所以设置的神经网络结构为6-12-1,即输入层有6个节点,隐含层有12个节点,输出层有个1节点,共有84个权值,13个阈值,所以萤火虫算法个体编码长度为97。其他参数设置见表1所列。

表1 GSO参数设置表
萤火虫算法优化过程中最优个体适应度值变化如4图所示。可以看出,萤火虫算法在种群为10的情况下,经过70次进化即收敛于最佳适应度值0.26,说明萤火虫算法仅需要很小的代价,就能寻找到最优BP神经网络权值和阈值。采用萤火虫算法优化BP神经网络的初始权值和阈值可行且高效。
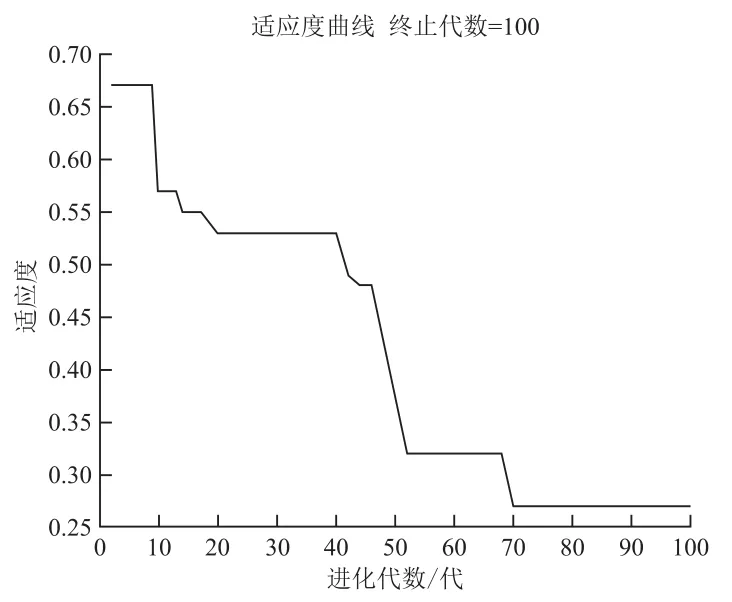
图4 GSO算法进化过程
3 补偿试验及分析
通过上述建模分析,建立了在不同温度条件下各进给轴的定位误差模型,并结合PMC端口[9]利用CNC系统中的D地址进行存储,调用R地址中的数值实现误差补偿控制。在VDM-75型机床上进行各进给轴补偿的试验取得了不错的补偿效果,波动幅度较小。热误差补偿实验对比结果如图5所示。

图5 热误差补偿实验结果对比
4 结 语
本文结合萤火虫算法和优化后的BP神经网络,建立了基于GSO-BP神经网络的数学模型,该模型在VDM-75型机床试验中证明,即使受到热误差环境的影响,误差波动范围最低也可减少43.6%。该方法具有概念简单、运算速度快、预测结果较准确等特点,具有一定的工程应用价值。
