测量误差对营养流行病学研究的影响及校正方法研究进展*

四川大学华西公共卫生学院/华西第四医院流行病与卫生统计学系(610041)胡逸凡 肖 雄 唐 丹 杨 帆 赵 星

测量误差是指测量值与真实值之间的差异。营养流行病学是受测量误差影响最严重、对测量误差关注度最高的流行病学研究领域[1]。其可能的原因在于，第一，膳食摄入很难直接测量，因而主要依靠“自报”式调查，如食物频率表、24小时膳食回顾调查等[2]。调查对象准确回忆膳食摄入量的难度较大，这种“自报”的调查方式通常会带来较大的测量误差[3]。第二，慢性病的发生被认为与长期膳食摄入而非短期食物摄入有关，因此通常需要关注长期膳食摄入量。然而，个体的膳食摄入情况本身存在波动，因此用某个时点收集的膳食数据来估计长期膳食摄入也会受随机误差的影响。

膳食研究可以分为膳食描述性研究和膳食与疾病间关联性研究。对于描述性研究，测量误差可能会使得观测到的膳食分布变异性更大，还可能使得膳食分布均值有偏[4]。对于关联性研究，测量误差不但会降低统计检验效能，使得研究所需样本量大大增加；通常还会导致单误差变量关联性分析的关联系数被低估(稀释偏倚)，从而使膳食与疾病之间的真实关联无法被检出；多误差变量关联性分析的关联系数可偏向任何方向，从而使得关联性分析结果不可信[5-7]。

鉴于测量误差在膳食数据中普遍存在，且对膳食研究造成严重影响，自20世纪70年代起，膳食领域涌现出许多关于测量误差校正的研究[3]。本文将对测量误差对膳食研究的影响和校正方法进行综述。

膳食领域常见的误差类型

测量误差可以分为随机误差(random error)和系统偏倚(systematic error)两大类[8]。随机误差在膳食领域通常指一个个体在不同时间点多次测量的膳食摄入与其长期膳食摄入之间的差异。仅含有随机误差的测量值是无偏的，因此可以通过重复测量的方式来减少误差。系统偏倚是指测量值始终朝一个方向偏离真实值。系统偏倚将造成测量值有偏，因此无法通过重复测量减少误差，只能用金标准测量值来校正误差。

1.经典测量误差模型

经典误差模型是最基本的测量误差模型，它假设测量值W为真实值加上均值为0，方差为Var(ε)的随机误差ε，且误差与真实值X独立，见公式(1)[9]。经典误差模型仅考虑了随机误差，没有考虑系统偏倚，即假设测量值相对于真实值是无偏的。然而“自报”式膳食调查工具获得的摄入量通常都是有偏的[3]，因此经典误差模型在膳食调查中通常无法满足。

W=X+ε

(1)

2.线性测量误差模型

线性误差模型(linear measurement error model)无需假设测量值无偏，因而被广泛用于描述膳食调查数据的测量误差，其模型假设见公式(2)[1]。其中位置偏倚(location bias)α0是与真实值X无关的偏倚；比例偏倚(scale bias)α是与真实值X成比例变化的偏倚。通常位置偏倚的取值大于0，比例偏倚的取值小于1，代表一种“坡度变缓现象”(flattened slope phenomenon)[10]，即真实摄入量较高者倾向于低报其摄入量，真实摄入量较低者倾向于高报其摄入量；随机误差ε均值为0，方差为Var(ε)，且与真实值X独立。当α0为0，α为1时，即为经典测量误差模型。

W=α0+αX+ε

(2)

3.异方差模型

在经典误差模型和线性误差模型中，都假设误差项ε的方差恒定，当该假设不能满足时，如散点图发现测量值的变异随着真实值增大而增大，可假设异方差模型(heteroscedastic error model)。假设公式(1)、(2)中ε的方差取决于真实值X的大小，且通常随着X增大而增大，表述为公式(3)[11]。在异方差模型的情况下，可尝试变量变换，如对数转换或一般的Box-Cox转换，使得方差齐，再使用上述同方差模型的误差校正方法[11]。

(3)

此外，根据误差是否与疾病结局相关，还可以将测量误差分为差分误差(differential error)和非差分误差(non-differential error)。非差分误差是指在给定真实值X和测量准确的协变量Z时，测量值W与疾病结局Y独立，可用公式表述为P(Y|W，X，Z)=P(Y|X，Z)[1]。通常认为在队列研究中，基线测量值的误差满足非差分误差模型，而在病例对照研究时，受回忆偏倚的影响，测量值的误差为差分误差[5]。上述经典测量误差、线性误差、异方差模型都属于非差分误差。差分误差对膳食研究的影响以及校正方法更加复杂。

测量误差对膳食研究的影响

膳食研究可以分为膳食描述性研究和膳食与疾病关联性研究两大类。膳食描述性研究是指通过膳食调查了解人群膳食摄入分布情况，中国居民营养与健康状况调查[12]及美国国家健康与营养调查(National Health and Nutrition Examination Survey，NHANES)[13]都属于这类研究。膳食与疾病关联性研究则更加常见，且探讨测量误差对其影响的研究也更多，本文探讨的重点在关联性研究。

1.膳食描述性研究

(1)经典误差模型

当调查的膳食变量存在经典测量误差时，由公式(1)可知E(W)=E(X)，Var(W)=Var(X)+Var(ε)，即调查的膳食分布均值无偏，但其膳食调查值的变异较真实的膳食摄入值变异更大。

(2)线性误差模型

当调查的膳食变量存在线性测量误差时，由公式(2)可知E(W)=αE(X)，Var(W)=α2Var(X)+Var(ε)，即调查的膳食分布均值有偏，由于α取值通常为0～1，故膳食调查值的变异较真实变异大小无法判断。

2.膳食与疾病关联性研究

测量误差对膳食与疾病关联性研究的影响取决于假定的测量误差模型以及疾病模型。本文仅探讨误差存在于连续性暴露变量的情况，对于错分类(misclassification)和结局变量存在测量误差的问题不作讨论。疾病模型中仅有一个含测量误差的变量称为单误差变量疾病模型，疾病模型中有多个含测量误差的变量称为多误差变量疾病模型。

(1)单误差变量疾病模型

①经典误差模型

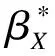
E(Y|X，Z)=β0+βXX+βZZ

(4)

(5)

(6)

(7)

②线性误差模型

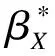
(8)

(2)多误差变量疾病模型

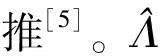
(9)

(10)

β=(ΛT)-1β*

(11)

(3)非线性疾病模型

以上结论都是从线性疾病模型推导而来，对于常见的非线性模型，如logistic回归模型，Cox比例风险模型，仍可近似得到以上结论。对于logistic回归，只要测量误差较小，或者真实的关联系数βX为低、中等大小，近似效果都较好[9]。对于Cox比例风险模型，若结局事件发生率极低，且失访对象为随机缺失，即保证随访过程中处于风险集中的个体协变量分布保持稳定，则测量误差的影响近似于线性疾病模型中的结论[14]。在不同情形下测量误差对膳食研究的影响总结于表1[1]。

表1 测量误差对膳食研究的影响

常见的测量误差校正方法——回归校正

一项关于膳食领域测量误差校正的综述显示，由于使用简单、适用性广等优点，目前90%以上的研究使用了回归校正法进行测量误差校正[15]。因此本文将回归校正法作为主要的误差校正方法进行阐述。对于一些营养素，如能量、蛋白质、钠、钾，可以使用恢复生物标志物(recovery biomarker)来准确测量其真实摄入量。虽然这种测量方式成本较高，但可以测量小样本的真实值来校正全人群含误差的测量值。然而目前可用的生物标志物非常有限[16]，对于许多食物和营养素无法测得真实值。我们从真实值已知和真实值未知两个方面来归纳回归校正法的使用。

1.真实值已知

(1)单误差变量疾病模型系数的校正

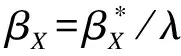
E(X|W，Z)=λ0+λW+λZZ

(12)

(13)

(2)多误差变量疾病模型系数的校正

多误差变量疾病模型系数的校正也可以用两种方法。第一种是按多误差变量疾病模型计算稀释沾染矩阵Λ，再按照公式(11)校正有误差的关联系数。第二种方式是先按公式(14)获得真实值的预测值E(X|W，Z)，其中Xi代表第i个含测量误差变量的真实值，共有n个变量含有测量误差。将预测值再带入疾病模型(9)中拟合的关联系数βX即为校正关联系数[11]。此时用Delta法计算多变量校正关联系数的方差较为复杂[18]，用bootstrap法计算校正方差更简便。

i=1…n

(14)

2.真实值未知

(1)测量值仅存在随机误差：经典测量误差模型

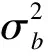
E(W2|W1，Z)=λ0+λW1+λZZ

(15)

(16)

(17)

(2)测量值存在系统偏倚：线性测量误差模型

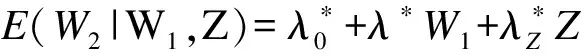
(18)

(19)

其他测量误差校正方法

1.模拟外推法

模拟外推法最早由Cook和Stefanski提出[21]，经Carroll发展完善[9]。模拟外推法的基本思想是在有测量误差的观测值上逐级增加测量误差，观察对关联系数的影响，然后外推到误差为0时的关联系数，即为真实的关联系数。与回归校正法相比，模拟外推法对于复杂的疾病模型更具有普适性，且无需知道部分样本的真值，但它只适用于经典测量误差模型。然而膳食数据通常无法满足经典测量误差假设，这可能是其目前在膳食领域应用有限的原因。

2.矩法重建法(moment reconstruction)

矩法重建法由Freedman[22]提出，它与回归校正法的相似之处在于都是寻找一个校正值来替代观测值。在回归校正法中是用给定测量值时真实值的期望作为校正值，而在矩法重建法中是用给定结局变量时与真实值的第一阶矩和二阶矩相等的值XMR作为校正值，即：E(XMR|Y)=E(X|Y)，Var(XMR|Y)=Var(X|Y)。矩法重建法在线性疾病模型中校正值与回归校正法校正值一致，而在logistic回归模型中，模拟研究显示其校正系数比回归校正法得出的校正系数更接近真实系数[22]。相对于回归校正法，矩法重建法考虑了结局变量信息，因此可以用于差分误差模型，而回归校正法只能用于非差分误差模型。

3.多重填补法(multiple imputation)

多重填补法本是由Rubin[23]提出用于缺失值填补的方法，Cola[24]提出将含有误差的连续性变量视作缺失数据，用多重填补法进行填补。多重填补通常会插补出多个数据集，将多个数据集数据分别与疾病进行关联后的关联系数用Rubin法则[23]进行合并。由于多重填补用到了结局变量的信息，因此与回归校正法相比，多重填补也可以用于差分误差模型的情况。

4.似然法(likelihood method)与贝叶斯法(Bayesian method)

Carroll[9]按是否对真实值假设分布，将测量误差校正方法分为两类：函数模型(functional models)和结构模型(structural model)，前者将膳食摄入量的真实值视为固定值，前述的所有方法都属于这一类；后者将膳食摄入量的真实值视为随机变量，服从一定的分布，这类方法包括似然法、贝叶斯法。结构模型依赖模型分布假设，而函数模型则不依赖模型分布假设。但在模型假设稳健性较好的情况下，结构模型在高度非线性等复杂的研究情境下结果更可靠。似然法的基本步骤如下：首先假设真实值X已经被观测到，从疾病模型出发，建立给定真实值X时疾病Y的分布；确定误差模型；基于前两步构建似然函数并最大化似然。贝叶斯法也需要构建似然函数，故与似然法有一些关联，但贝叶斯法将参数视为随机变量，最终得到待估计参数的后验分布。相对于似然法，贝叶斯法更受欢迎，这可能与WinBuGs等自动软件的使用大大降低了计算难度有关。

讨 论

近年来，营养流行病学研究的可靠性倍受争议，膳食数据测量误差严重是原因之一[3，25]。本文综述了目前测量误差对膳食研究的影响和校正方法，希望能提高营养流行病学研究者对测量误差的重视程度，并方便研究者们选择合适的误差校正方法使膳食研究结果的可信度更高。

测量误差会使得膳食因素与疾病之间的关联估计不准确。由于膳食数据通常含有系统偏倚，因此需要“金标准”校正。然而，大部分膳食数据没有“金标准”测量方法。24小时膳食调查(24HDR)数据以随机误差为主，系统偏倚较小[26]，因此目前多次24HDR数据通常被作为膳食研究校正的参考测量方法[16]。为了达到金标准校正效果，参考测量方法至少需要满足两个假设，即参考测量方法的误差与主调查工具的误差不相关，且与真实值不相关，然而这两个假设24HDR均不满足[27]。有研究对蛋白质、钾、碘等有“金标准”测量的营养素，用24HDR这种“伪金标准”校正的后果进行了探究，结果显示24HDR会高估稀释因子的大小，从而低估这些膳食因素与疾病之间的关联[16，27-28]。因此，研究者们也在不断开发衡量膳食摄入的客观指标，如浓度生物标志物(concentration biomarkers)[29]、基于代谢组学的膳食标志物(metabolomics-based dietary biomarkers)[30]等。

测量误差通常会降低统计检验效能，且此问题无法通过误差校正解决，其最直接的影响是使研究所需样本量大大增加。因此，膳食研究通常需要很大的样本量[5]。如美国癌症中心开展的NIH-AARP队列纳入了188 736名绝经后女性，探究从脂肪中摄入能量占总能量比例与乳腺癌发病的关联，结果显示风险比的95%置信区间仅为1.00～1.24[31]。若非大样本研究，则很可能无法发现一些膳食因素与疾病之间的关联，目前仍可能有许多膳食因素与疾病的关联被测量误差掩盖。

由于使用简单和适用性广，回归校正法是目前最受欢迎的测量误差校正方法。该方法通过建立真实值与测量值及协变量的线性回归来估计校正值，然而该线性假设不一定能满足。在非线性等复杂疾病模型情况下回归校正法的校正效果可能较差[9]。今后在使用回归校正法时应该充分考虑回归校正法的适用条件，如当参考测量方式并非金标准时开展敏感性分析。此外，应该多尝试回归校正法之外的其他误差校正方法，并进一步发展新的测量误差校正方法。