基于组合赋权的水利工程基础设施PPP项目风险综合评价

孙维民

（山东省水利工程局有限公司,山东 济南 250000）

0 引言

基础设施PPP项目具有建设周期长、投资大以及资金回笼慢等特点,也决定了在项目建设过程中面临着诸多的风险。在风险评价方面,陈斌、王蕾等人构建了PPP项目风险指标体系,并建立AHP—熵值法评价模型,对识别出的风险指标进行赋权,根据权重数值大小确定各风险因素对PPP项目的影响程度。石振武、宋莹琪等人提出德菲尔调研法、网络分析法、模糊综合评价法相结合的Delphi—FANP风险评价模型。王帅、郝生跃等运用粗糙集理论对风险因素进行约简,利用熵值法与G1 法综合集权的方式进行权重赋值,为构建海绵城市PPP项目风险评价提高新的方式。鉴于风险评价工作比较看重行业专家的实践经验,本文提出AHP（层次分析法）—CPA（变异系数法）主客观相结合的组合赋权法对基础设施PPP项目风险指标进行评价。

1 基础设施PPP项目风险指标体系的建立

结合基础设施PPP项目特点,根据项目生命周期特点划分为决策阶段、准备阶段、实施阶段及运营阶段四个阶段,对每阶段的风险因素进行识别,再将风险因素划分为经济、建设、法律、政治、运营与市场收益六个层面,形成六个一级指标、25 个二级指标的基础设施PPP项目风险指标体系,见表1。

表1 基础设施PPP项目风险指标体系

2 模型的构建

2.1 层次分析法

层次分析法（AHP）是一种评价者通过分析复杂系统所包含的因素以及相互关系,将问题或者对象系统分解为多个层次并注入深入进行分析的方法。

第一步：构造两两判断矩阵。层次结构反应因素之间的关系,判断矩阵表示针对上一层元素而言评价层各元素的相对重要性。

第三步：对矩阵进行一致性检验。

1）计算一致性指标CI：

2）计算一致性比例CR：

当CR＜0.10时,判断矩阵的一致性是可以接受的,否则需要对判断矩阵进行调整,直到满足条件为止。

第四步：计算二级指标对总目标的合成权重。求出二级指标相对总目标层的权重向量为W0=（W10,W20,…WN0）T,则：

式中：Wi1、Wi2分别表示一级指标与二级指标相对总目标层的归一化权重。

2.2 变异系数法

变异系数法（CPA）是一种根据各个指标在所有被评价对象上观测值的变异程度大小对其进行赋权的方法。其核心思想是通过指标的变异系数来衡量各评价值的差异程度。

第一步：对评价指标进行无量纲化处理。设Xik表示第i个评价指标中第k个评价对象的权值,m为被评价对象的数量,Yik表示无量纲化处理后第i个评价指标中第k个评价对象的权值。

第二步：计算各指标的变异系数。设变异系数为δi,1≤i≤N,则：

其中,

第三步：计算各指标的变异系数权重,并对变异系数进行归一化处理。

得出二级指标变异系数权重向量为W=（W1,W2,…WN）T。

2.3 组合赋权模型的构建

通过层次分析法得到所有二级指标相对总目标的主观权值向量：W0=（W10,W20,…WN0）T。通过变异系数法得到所有二级指标相对总目标的客观权值向量：W=（W1,W2,…WN）T。则组合向量权重为：ζ=（ζ1,ζ2,…ζN）T,其中

α、β表示组合权重中的线性表示系数。其中α≥0, β≥0,α2+β2=1。

假设所有评价指标之间的总离差为Ω,则：

基于离差最大化思想,建立最优模型,如下：

2.4 模型求解

构建Lagrange函数：

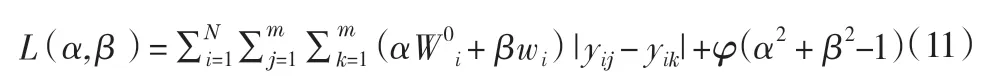
其中, φ为Lagrange乘子,之后对L（α,β ）求导,令：

求解,得出：

求出α、β后带入组合权向量：ζ=aW0+ βW,进行归一化处理,最终得到评价结果。

3 实证分析

某市计划兴修某水利枢纽工程,总工期为三年。本项目计划采用PPP模式进行建设,社会资本与地方政府部门组成平台公司（spv）,负责项目的融资、建设以及后期的运营维护工作,特许经营期为20 年。

3.1 主客观赋权

首先,邀请相关行业专家和一线工作者根据Saaty1-9 级标度法对系统层指标进行两两打分并计算权重；其次,采用变异系数法计算客观赋权权重,本文利用matlab软件进行计算,结果见表2。

表2 系统层判断矩阵计算结果

其次,依旧根据行业专家和一线技术人员进行两两打分,计算二级指标权重,具体见表3~表8。

表3 经济风险指标判断矩阵计算结果

表4 建设风险指标判断矩阵计算结果

表5 法律风险指标判断矩阵计算结果

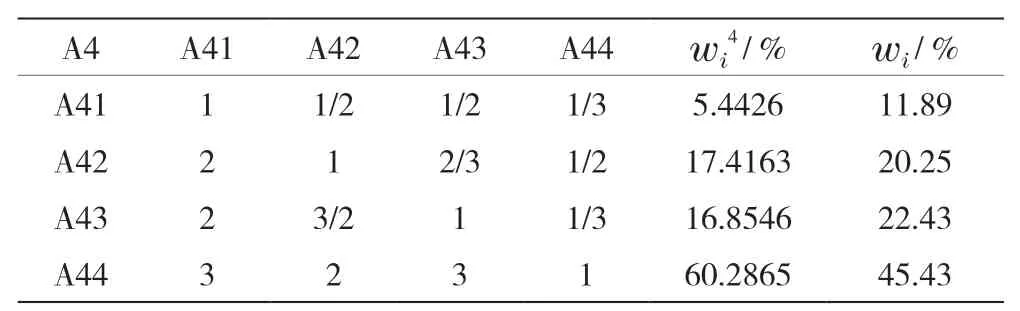
表6 政治风险指标判断矩阵计算结果

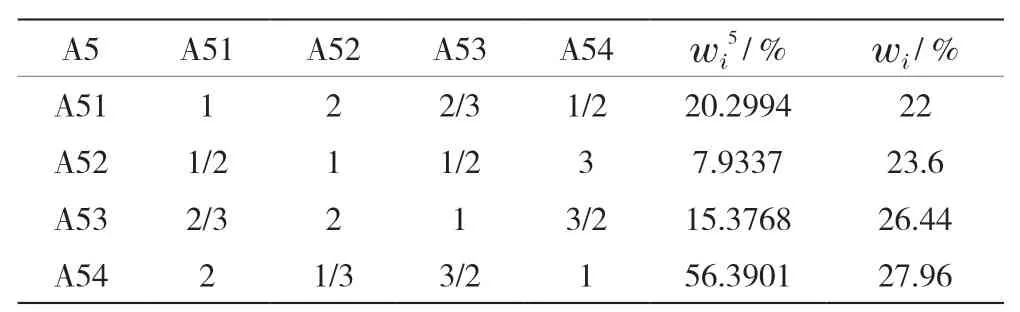
表7 法律风险指标判断矩阵计算结果

表8 市场收益风险指标判断矩阵计算结果

3.2 组合赋权

在求得主观权重与客观权重之后,将权重数据代入公式（13）,得出α=0.5918,β=0.8061。利用公式求得组合权重,并进行归一化处理,具体数据见表9。

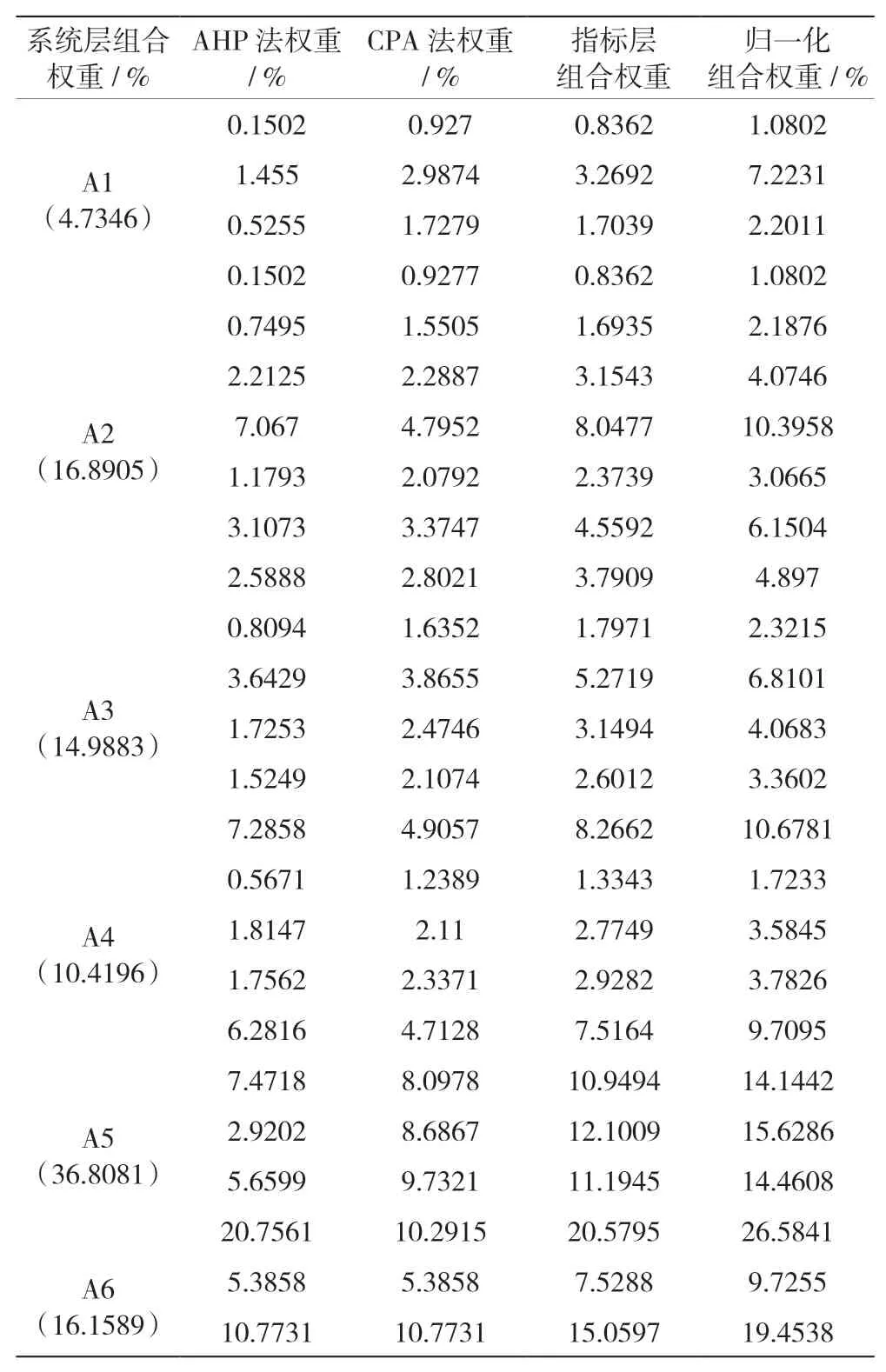
表9 权重处理结果

层析分析法与变异系数法组合赋值二级指标权重计算结果为：ζ=（0.8362,3.2692,1.7309,0.8362,1.6935,3.1543,8.0477,2.3739,4.5592,3.7909,1.7971,5.2719,3.1494,2.6012,8.2662,1.3343,2.7749,2.9282,7.5164,10.9494,12.1009,11.1945,20.5795,7.52 88,15.0597）。

将二级指标综合权重进行归一化处理,得出最终二级指标综合权重：ζ=（1.0802,7.2231,2.2011,1.0802,2.1876,4.0746,10.3958,3.0665,6.1504,4.897,2.3215,6.8101,4.0683,3.3602,10.6781,1.7233,3.5845,3.7826,9.7095,14.4608,26.5841,9.7255,19.4538）。

系统层指标综合权重：ζ=（4.7346,16.8905,14.9883,10.4196,36.8081,16.1589）。

系统层指标综合排名为：A5＞A2＞A6＞A3＞A4＞A1,即就风险指标评分而言,运营风险＞建设风险＞市场收益风险＞法律风险＞政治风险＞经济风险。因此在项目生命周期中,要积极制定运营阶段和建设阶段的风险应对策略。在指标层中,建设成本超支风险、法律变更风险、运营成本超支风险、残值风险、环境污染风险、不可抗力风险与市场竞争风险的综合评价得分均高于10,表明风险发生的可能性较高,应提前制定针对性的应对方案,达到避免或者减轻风险带来的损失。

4 结论

运用AHP-CPA组合的赋权方法对水利工程PPP项目风险进行综合评价,克服了层次分析法主观性太强的问题,同时,也解决了忽视专家经验的缺陷,使得主客观权重更合理。从建立的PPP项目风险评价模型来看,评价过程清晰,计算相对简单,实现了对工程PPP项目风险因素的定量评价。由此可见,这种风险评价方法不仅克服了单一评价方法的不足,也使得整个风险评价过程更具有可操作性,评价的结果更科学合理,有利于PPP项目的建设发展。