物流中心选址问题的二元语义决策方法*
2021-10-09魏宗田
师 铭 魏宗田
(西安建筑科技大学理学院 西安 710055)
1 引言
随着我国物流行业的快速发展,物流中心选址问题[1-2]受到众多学者的关注。目前,传统的研究方法主要有重心法[3]、整数规划法[4]、层次分析法[5]等。但重心法无法求出物流中心的最优位置,整数规划法对于规模较大的问题难以求解,层次分析法易受主观影响,评价过程比较粗糙。Herrera教授于2000年提出二元语义评价方法[6],在一定程度上可以避免语言评价中信息的损失和扭曲。本文引入三角模糊数将语言评价信息量化,再通过二元语义对物流中心选址方案进行综合评价,使计算结果更加精确。
2 基于二元语义的物流中心选址方法
2.1 构建物流中心选址的指标体系
物流配送中心的选址理论最初由Weber于1909年提出[7]。物流配送中心选址是指在一个具有若干供应点及若干需求点的经济区域内,选取一定数量的地址设置配送中心的规划过程[8~9]。在物流中心选址过程中应同时遵守适应性原则、协调性原则、经济性原则和战略性原则。徐杰、郑凯等[10]将相关影响因素进行分组,对物流中心选址的指标划分为以下几个层次。
1)目标层表示决策的目的和要解决的问题。将物流中心选址方案的综合评价作为目标层。
2)准则层表示考虑的因素和决策的准则即采取方案所涉及的中间环节。根据物流中心选址原则,将自然环境、经营环境、基础设施状况、其他四个因素作为准则层。
3)指标层表示决策时的备选方案。在充分考虑准则层影响因素的情况下,指标层可分为气候条件、地质条件、水文条件、地形条件等十三个因素。物流中心选址的指标体系如图1所示。
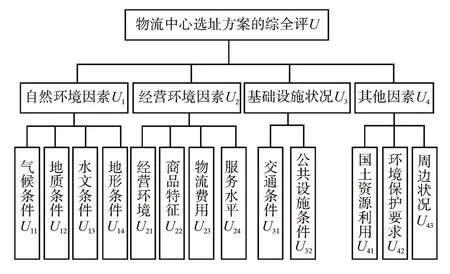
图1 物流中心选址的指标体系
本文使用此体系建立物流中心选址模型,引入三角模糊数对各评价指标量化,用二元语义对物流中心选址方案进行综合评价,从而选出最优方案。
2.2 二元语义及其集结算子
二元语义[2,10~15]是利用一个二元组(si,αi)表示语言评价信息,其中si表示预先设定好的语言评价集中 第i个 语 言 短 语,αi表示评价语言与si之间的偏差。
定义1定义映射θ:S→S×[0 .5,0.5],利用θ将si转化为二元语义形式:
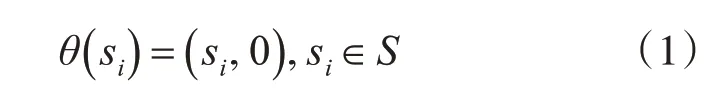
定义2定义映射Δ:[0 ,g]→S×[- 0.5,0.5],即

其中β(∈[0 ,g])表示si通过集结运算得到的实数。i=round(βg),round(·)表示四舍五入取整运算;。
定义3定义Δ的逆映射Δ-1:S×[- 0.5,0.5]→[0 ,g],将(si,αi)映射成数值β,即

定义4设(sm,αm)和(sn,αn)是两个二元语义,则有如下性质:
1)当m>n时,(sm,αm)>(sn,αn)。
2)当m=n时,
(1)如果αm=αn,则(sm,αm)=(sn,αn);
(2)如果αm>αn,则(sm,αm)>(sn,αn);
(3)如果αm<αn,则(sm,αm)<(sn,αn)。
其中,“<”表示“好于”,“=”表示“等于”,“<”表示“差于”。
由于映射Δ和Δ-1可以毫无信息损失地将数值转换为二元语义形式,所以一些数值集结算子被用来处理二元语义信息。目前常用的二元语义集结算子主要有以下两个[2]。
1)二元语义算术平均算子(T-AA)
假设二元语义评价集合{(s1,α1),(s2,α2),…(sn,αn)},则二元语义的算术平均算子定义为
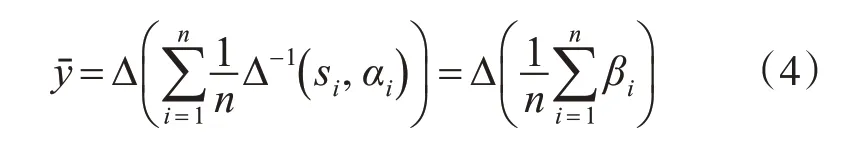
2)二元语义加权平均算子(T-WA)
假设二元语义评价集合为{(s1,α1),(s2,α2),…(sn,αn)},其中(si,a)i对应的权重为wi,i=1,2,…,n。则二元语义加权平均算子定义为

2.3 问题描述
根据物流公司的要求,需要在某地区设置一个物流中心。现有n个物流中心备选点,记集合X={X1,X2,…,Xn},Xi表示第i个备选点,其中i=1,2,…,n。物流中心选址的指标集U={U1,U2,…,Um},其中Uj表示影响因素依次对应图1各指标,其中j=1,2,…,m。设有k个决策专家参与选址决策,记集合E={E1,E2,…,Ek}。决策专家Eg从事先设定好的语言评价集S和权重评价集Sw中选择一个元素作为对物流中心备选地址Xi对应指标Uj的评价值,其中,g=1,2,…,k。语言评价集S和权重评价集Sw是事先设定好由奇数个元素组成的集合。
2.4 决策步骤
物流中心选址的二元语义决策步骤如图2所示。
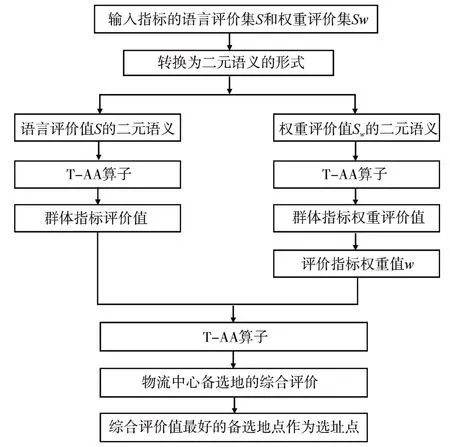
图2 二元语义决策步骤
Step1:通过θ(si)=(si,0),si∈S将专家组的评价等级和权重语义评价短语转化为二元语义形式。
Step2:利用二元语义算术平均算子(T-AA):对专家组给出自然语言评价值和权重值集结。
Step3:利用Δ(β)=(si,αi)求得各级指标的评价等级和权重的二元语义。
以备选地址X1为例,将专家组的定性评价评价结果转换为二元语义形式,见表7。
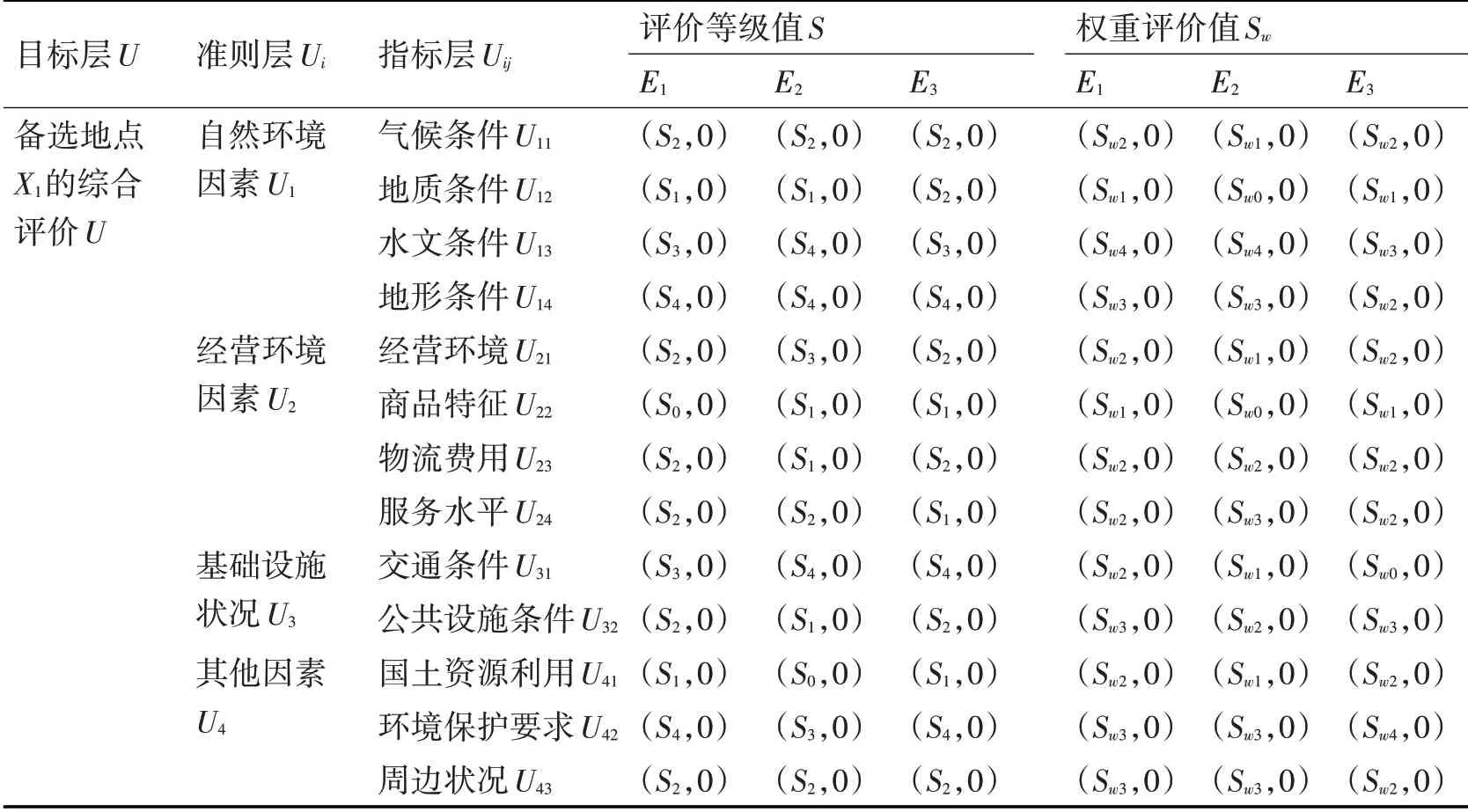
表7 备选地点X1各指标的语言评价值的二元语义和权重评价值的二元语义
以“自然环境因素U1”下的“气候条件U11”这个评价指标为例,利用二元语义算术平均算子(T-AA)计算其值为U11=(S2,0),W11=(Sw2,-0.08)。
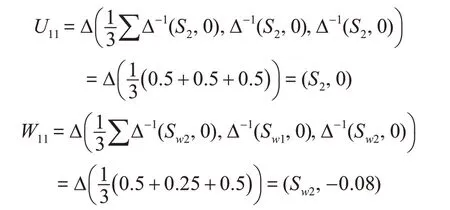
3 算例分析
根据某物流公司的要求,需要在某地区设置一个物流中心。经过初步考察和分析,该区域有四个备选点,结合物流中心选址方案评价体系。建立物流中心语言评价集S的三角模糊数(表1)和权重评价集Sw三角模糊数(表2)。
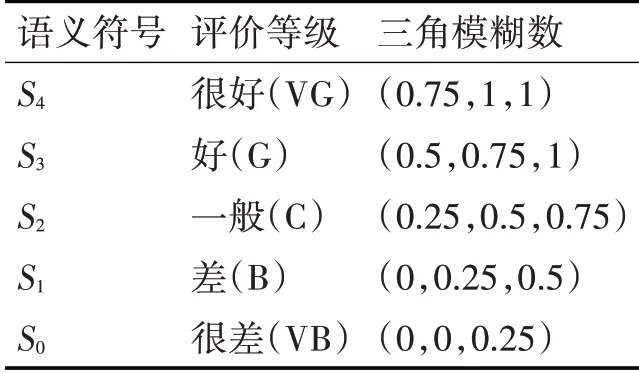
表1 语言评价集S的三角模糊数
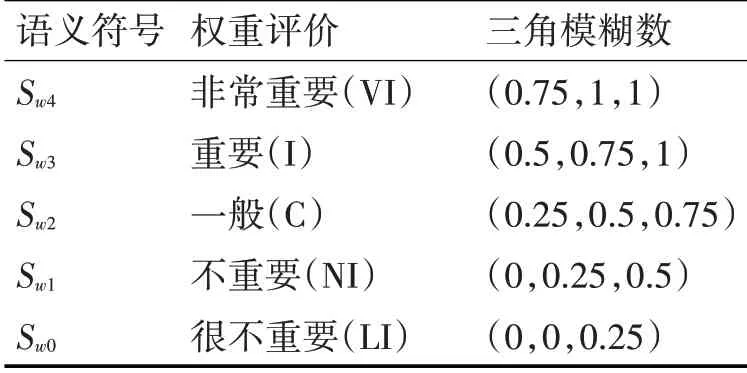
表2 权重评价集Sw的三角模糊数
三名相关专家依据既定指标和备选地址的具体情况对物流中心选址进行决策。三位专家对四个备选地址给出的评价等级值S和权重评价值Sw具体见表3~表6。
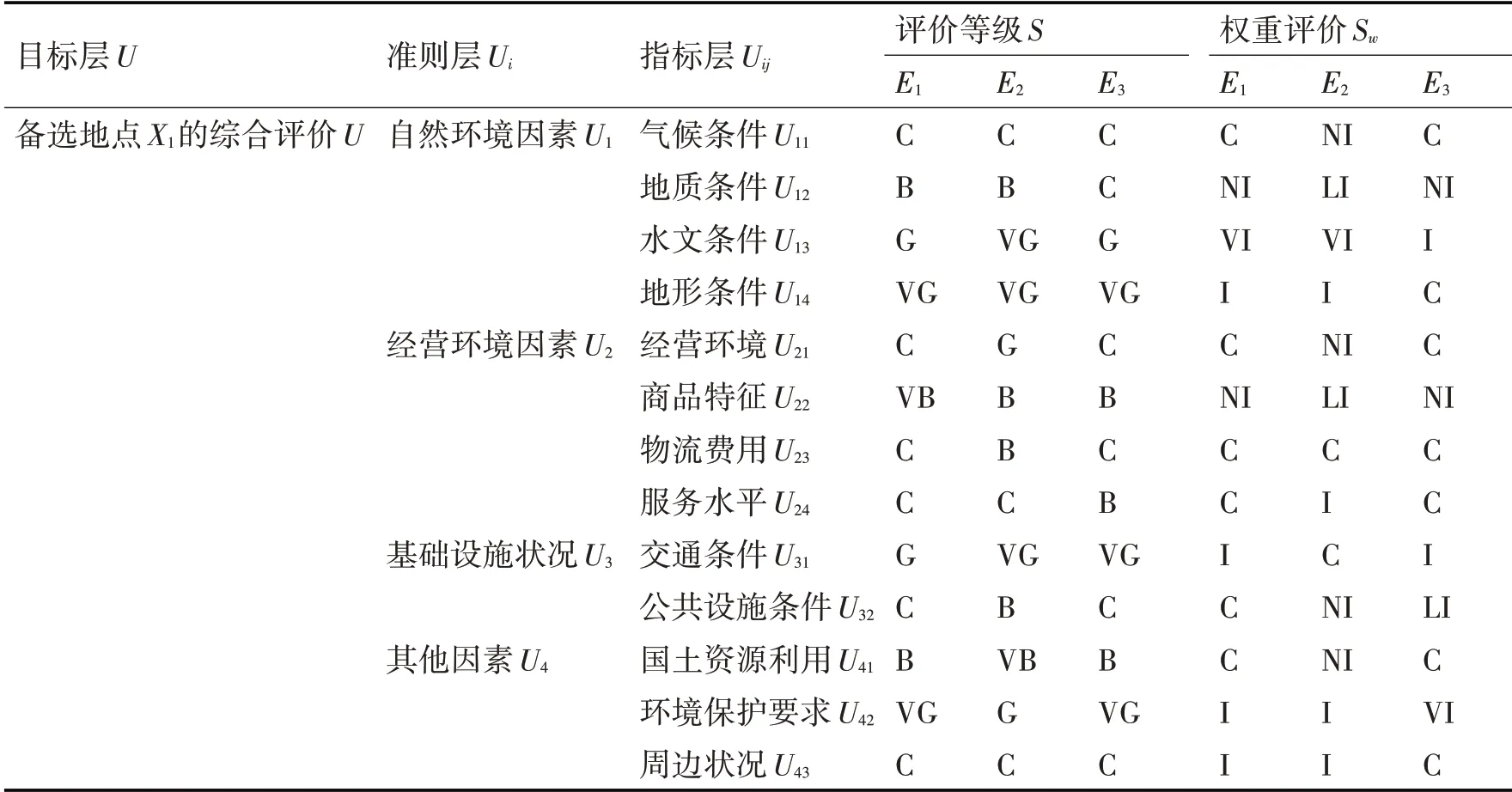
表3 专家对备选地点X1各指标的语言评价和权重评价
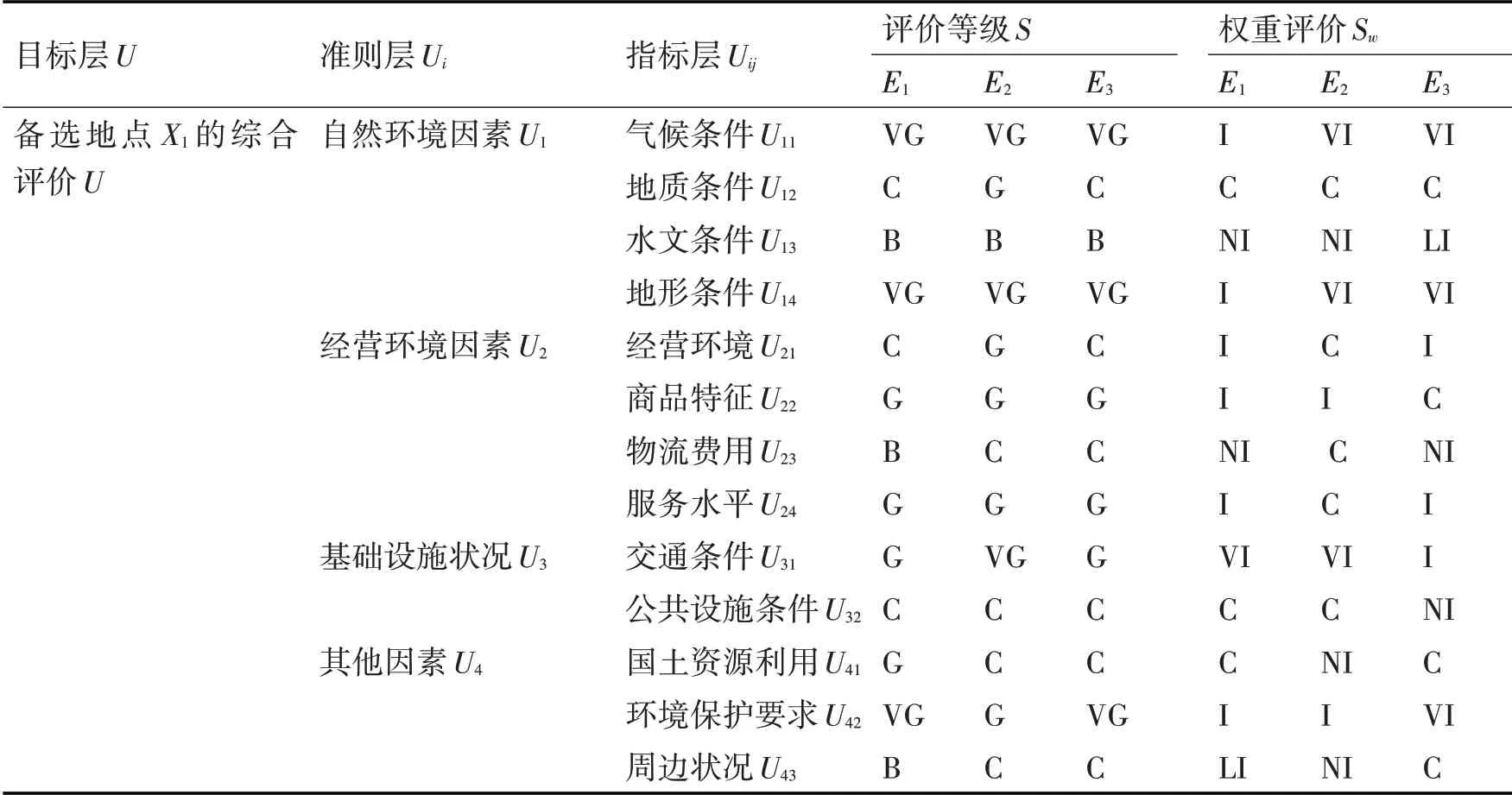
表6 专家对备选地点X4各指标的语言评价和权重评价
同理可得其余评价指标的测算结果,见表8。

表8 指标层评价指标的测算结果
以“自然环境因素U1”为例,用T-WA算子计算得为U1=(S3,0.03),用T-AA算子计算得为W1=(Sw2,-0.08)。
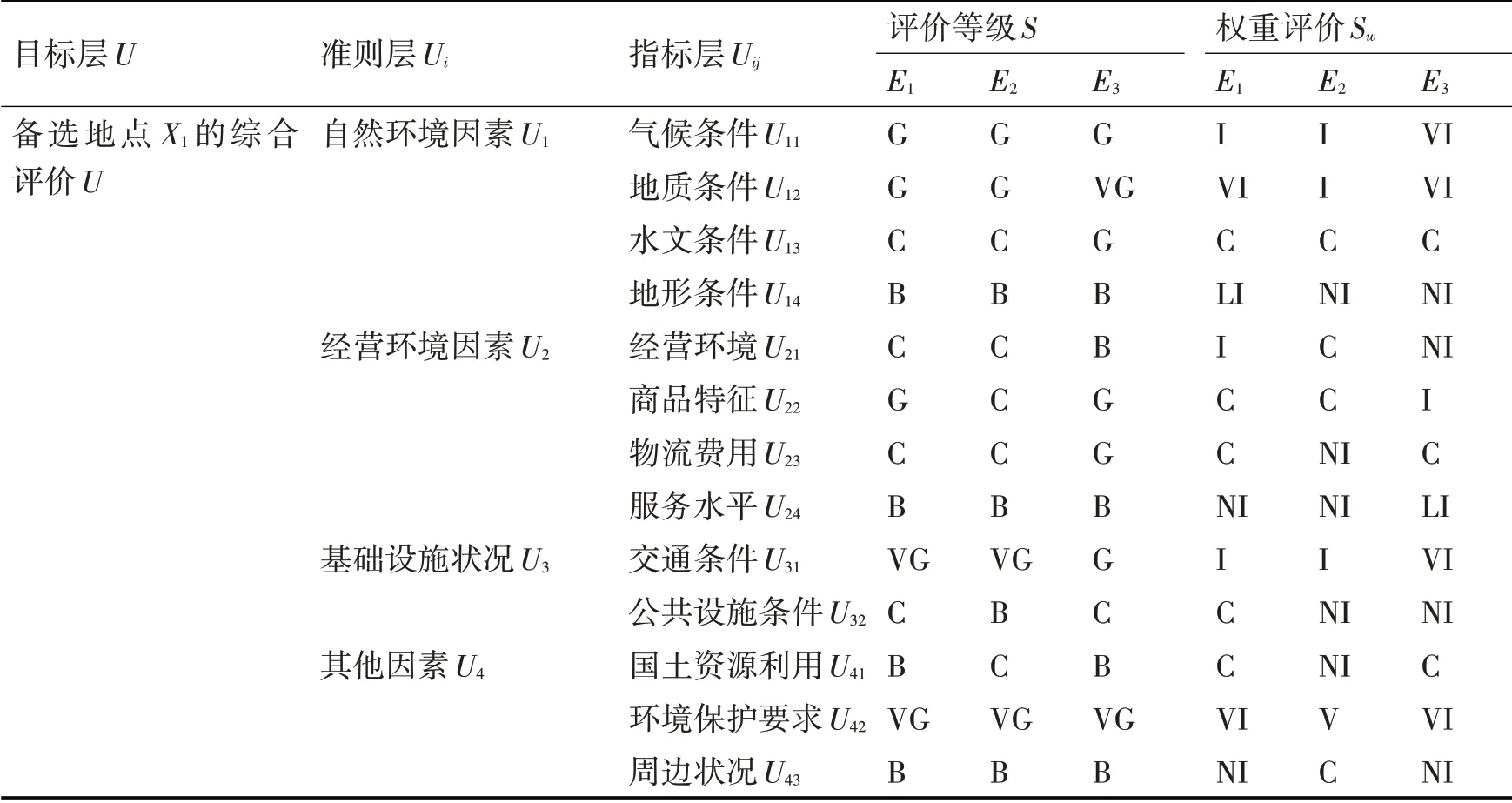
表4 专家对备选地点X2各指标的语言评价和权重评价
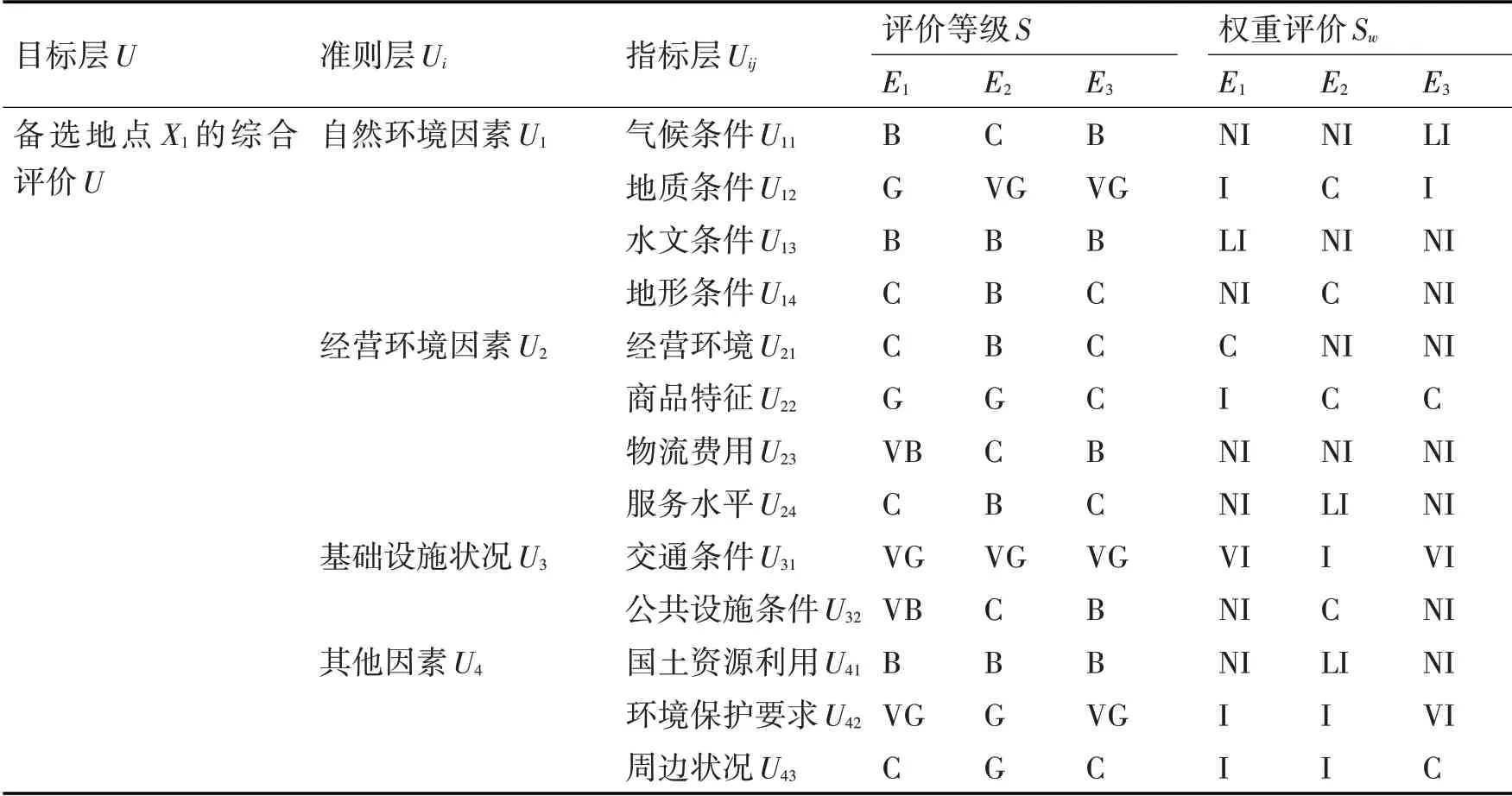
表5 专家对备选地点X3各指标的语言评价和权重评价
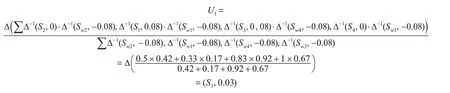
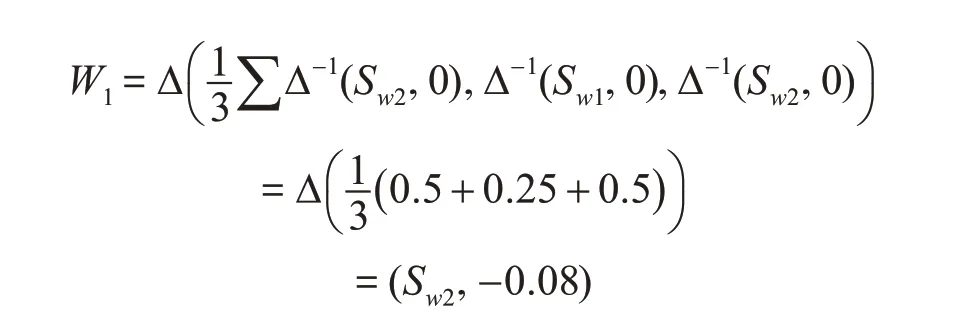
同理可得其余评价指标的测算结果,见表9。
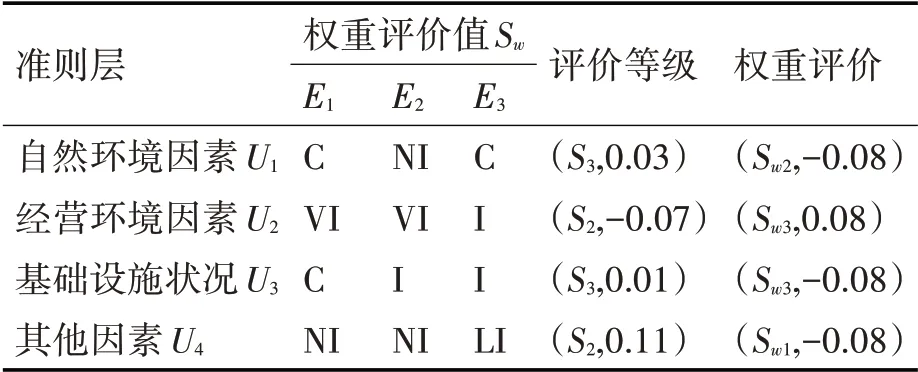
表9 准则层评价指标的语言评价值和权重评价值
通过T-WA算子测算求得备选地址X1的综合评价结果。

同理,采用二元语义T-WA算子,对每个物流中心备选点各个指标群体评价值进行集结计算,从而获得各个备选点的综合群体评价值如表10。

表10 各个备选点的综合群体评价值
通过各个物流中心备选点的综合群体评价值可以看出,物流中心最佳选址点为第四个物流中心备选点。同时,根据定义四对各个物流中心备选点的优劣排序为X4>X2>X3>X1。
4 结语
物流中心选址问题的复杂性及影响因素的不确定性,使得备选地址很难精确量化。本文通过引入三角模糊数将不确定影响因素定量化,提出了基于二元语义的物流中心选址方法,该方法可以有效避免收集和计算语言评价信息过程中的信息丢失和失真,使语言信息的计算结果更加准确,在物流中心选址决策中具有更好的实用性。
