走出误区 走向光明

徐永清

同学们在运用全等三角形的性质和判定解决问题时，常会因为一些误区而做错题目。只有找出错因，克服盲点，才能走向光明。下面列出一些本章的易错题，同学们可以试着做一做，对易错类型进行總结，避免在同一类问题上犯同样的错误。

易错类型1：不能正确找出全等三角形中的对应边、对应角

1.如图1所示，点E在△ABC外部，点D在BC边上，DE交AC于F，若∠1=∠2=∠3，AD=AB。猜想AC与AE之间的数量关系，并说明理由。

考点：全等三角形的判定和性质、三角形的内角和定理。

易错类型2：不能正确运用三角形全等的条件

2.如图2，已知AC=DB，要使△ABC≌△DCB，只需增加的一个条件是（）。

A.∠ABC=∠DCB   B.∠ACB=∠DBC

C.∠ABD=∠DCA   D.∠A=∠D

考点：全等三角形的判定。

易错类型3：在运用全等三角形的知识解决问题时思考不全面

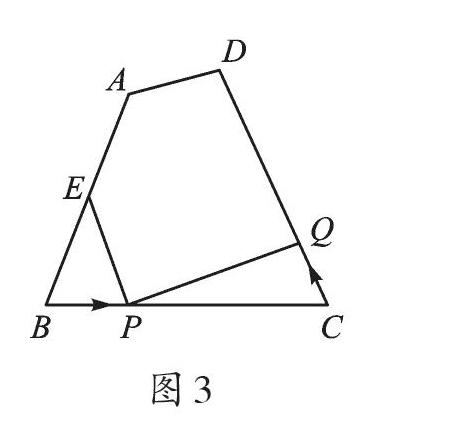
3.如图3，已知四边形ABCD中，AB=10厘米，BC=8厘米，CD=12厘米，∠B=∠C，E为AB的中点。如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动。当点Q的运动速度为               厘米/秒时，△BPE与△CQP全等。

考点：全等三角形的判定。

（作者单位：江苏省盐城市腾飞路初级中学）