型钢混凝土闸墩的时变可靠度分析
2021-10-08张小飞肖天培
吴 健,张小飞,陈 丹,肖天培,覃 培
(广西大学土木建筑工程学院,广西 南宁,530004)
0 引 言
闸墩是一种用于支承闸门、分隔闸孔及连接两岸的墩式结构。作为水利枢纽泄水建筑物的重要组成部分,随着大流量、高水头泄水建筑物的不断增多,闸墩承受的作用力越来越大,单纯采用普通钢筋混凝土结构难以满足大推力闸墩结构的安全要求。以型钢代替普通钢筋混凝土闸墩中扇形钢筋的新型闸墩结构被提出[1-3],初步研究表明,型钢混凝土闸墩具有刚度大,承载力高等优点,能较好地满足大推力情况下闸墩承载能力的要求。
由于型钢混凝土闸墩是一种由多种材料构成的复杂结构,很难采用传统积分方法求解其结构可靠度。目前对于型钢混凝土闸墩的结构可靠度方面研究还比较少,尤其是时变可靠度。Yasuhiro[4]提出了一种结合条件期望的自适应蒙特卡罗模拟方法,并验证了此方法对结构的时变系统可靠度分析的可行性,认为自适应重要抽样评估系统失效概率的精度对概率的顺序相对不敏感。田浩[5]等建立了基于改进响应面法和确定性的混凝土桥梁退化过程分析方法相结合的混凝土桥梁时变可靠度分析方法,克服了复杂体系结构极限状态方程通常是隐式的问题,实现了混凝土桥梁时变可靠度的求解目标。本文借鉴已有的研究成果,把时间作为变量,利用ANSYS概率设计模块的响应面法拟合出响应面方程,并将拟合方程作为闸墩的功能函数进行可靠度分析。利用得出的响应面方程结合JC法求解型钢混凝土闸墩在不同时间点的可靠指标,研究其在设计基准期内的可靠指标的变化趋势,并通过灵敏度图分析闸墩的型钢尺寸、型钢屈服强度、混凝土抗压强度等参数对闸墩可靠度的影响。
1 结构可靠度分析
1.1 结构可靠度分析的响应面法
实际工程中,结构复杂的工程基本随机变量存在各种不确定性,用结构可靠度理论的传统积分方法难以确定极限状态功能函数的显式方程,进而计算结构的可靠度。因此,求解复杂结构的可靠度需采用新的计算方法。目前,主流的结构可靠度计算方法包括二阶矩法、蒙特卡罗法[6]以及响应面法。其中响应面法是针对隐式功能函数的一种有效可靠的建模和计算方法。其原理是选用一个适当的、可以明确表达的响应面函数来近似代替无法明确表达的真实函数,即通过一些确定性的数值模拟和试验研究,并通过有限次的计算拟合出响应面,以代替未知的、真实的极限状态曲面。具体实现方法是利用ANSYS所建立的简化有限元模型,根据结构参数的不确定性来定义输入变量,利用输入变量的均值、标准差以及参数服从的分布类型,根据失效模式定义输出变量,进而利用ANSYS中概率设计模块自动进行抽样再拟合得出所需的输出变量。目前响应面函数的主要形式是二次多项式,其形式分为包含交叉项和不包含交叉项两种。考虑到计算效率和精度问题,本文采用包含交叉项的二次多项式,函数形式如下:

式中:a,bi,dij(i=1,2,…,n)表示公式中的待定系数;Z表示结构的功能函数;Xi,Xj表示影响结构的随机变量。
公式中的待定系数可以通过样本点拟合进行求解,其中样本点的选取通过试验设计的方法实现。常用的试验设计包括二水平因子设计和中心复合设计。为保证拟合响应面函数的精度并减少计算代价,本文采用中心复合设计。拟合的响应面示意图如图1所示。

图1 响应面示意图
1.2 可靠指标的计算
计算结构可靠度指标可利用得出的响应面方程结合JC法进行计算,即用ANSYS所得出的响应面方程作为能够表征结构可靠度的功能函数,再根据JC法计算结构的可靠指标。JC法是一种通过当量正态化将非正态随机变量等价为正态分布的可靠指标计算方法。由于本文通过响应面法得出的输出变量并不确定其分布形式,仅得出了响应面函数,利用JC法计算结构可靠指标较为合理,该方法适用于随机变量为任意分布下结构可靠指标的求解,运算简捷,且对非线性程度不高的结构功能函数,其精度能满足工程实际需要,并已为国际联合委员会(JCSS)所采用[7],其表达式见式(2)。

式中:β(t)表示结构的可靠指标;μz(t)表示Z的均值;σz(t)则是Z的标准差。
在分析型钢混凝土闸墩的时变可靠度时,难以得到每个参数的统计资料以及其变化的随机性,且某些参数随时间变化幅度非常小,因此在分析时只考虑随时间变化敏感的参数。对于型钢混凝土闸墩而言,把每一时刻都作为研究对象,这是不切实际的。目前对结构时变可靠度的研究主要是转化成时不变可靠度,即认为在某个时间段或某个时间点的可靠度保持不变,通过研究在设计基准期内多个时间点的可靠度来表示结构在整个设计基准期内的时变可靠度。考虑到计算的复杂性,本文以10年作为一个时间点,通过研究型钢混凝土闸墩的时不变可靠度,进而对整个基准期内的可靠度进行分析。
1.3 闸墩结构灵敏度分析
灵敏度分析是研究与分析一个系统(或模型)的状态或输出变化对系统参数或周围条件变化的敏感程度的方法。在结构运行过程中,材料、几何参数的变化会影响结构的承载能力,对结构进行敏感度分析可以确定影响可靠度较大的参数,有利于保证结构的安全。本文通过在响应面方程上进行蒙特卡罗抽样,得出影响参数的灵敏度图,分析得到对结构可靠度影响较大的因素,按照要求提高或降低其数值来实现结构的优化。
2 闸墩有限元模型建立及模型参数确定
2.1 有限元模型建立
为了更贴近实际,本文按广西邕宁水利枢纽泄水闸坝的结构形式和尺寸建立三维有限元模型,取一个长41.6m的独立坝段作为分析对象,闸墩高38.2m、厚3.2m,闸坝结构按力学计算模型进行了一定程度的简化。根据《水工混凝土结构设计规范SL191-2008》的相关公式计算确定型钢的配钢量为800cm2,取型钢尺寸为415mm×363mm×26mm×26mm(型钢高度×型钢宽度×翼缘厚度×腹板厚度)。型钢的布置方式根据相关研究[1,2,8-10]采用三型钢,保护层厚度为 400mm,长度为20m,角度为25°的布置方式,并在闸墩两侧内配置横、竖向构造钢筋,同时设有横向联接型钢。闸坝的有限元模型如图2、图3所示。

图2 闸坝有限元模型示意图

图3 单侧型钢有限元模型示意图
闸坝有限元模型的墩体和堰体采用C30混凝土,牛腿支座处选取C40混凝土。工程安全等级为Ⅱ级,破坏类型为2类。采用solid65单元对混凝土进行模拟,选用随动强化模型(MISO)对混凝土单元进行分析,破坏准则为William-Wamke五参数破坏准则。根据文献[2],型钢混凝土闸墩中布置的型钢为Q345牌号H型钢,采用beam188单元模拟型钢,其本构关系选用多线性随动强化模型(MKIN)。
根据工程中实际运行情况,本文考虑了两侧弧形闸门均关闭的对称工况和一侧闸门关闭,另一侧闸门开启的非对称工况,基于广西邕宁水利枢纽泄水闸坝的设计资料,不同工况下所受的弧门推力荷载如表1所示,弧门闸墩牛腿支座各方向受力示意图如图4所示。弧门支座承受来自弧形闸门的推力作用,通过牛腿处的型钢和混凝土将荷载传递到整个闸墩,为避免施加荷载的过程中因局部施加荷载而导致局部应力集中,出现假收敛与实际不符的现象,在牛腿支座的荷载受力面施加均布面力荷载。均布荷载的大小是单位受力面积下的弧门单侧推力,受力面积为2.2m×4.6m。此外,在将弧门单侧推力作为变量时,需考虑其均值系数,根据文献[11],本文取均值系数为1.08。

表1 闸墩牛腿支座处在闸门关闭或开启时受力情况 kN

图4 闸墩牛腿支座受力简图
2.2 模型输入参数
响应面方程中 G、SFC、TFC、FFC、T、W 分别是闸墩的输入参数,包括弧门均布荷载、型钢强度、墩体混凝土抗压强度、牛腿处混凝土抗压强度、型钢厚度、型钢宽度,其取值如表2。

表2 型钢混凝土闸墩统计参数
由于型钢的保护层厚度较大,在设计基准期内型钢出现锈蚀的可能性不大,型钢的强度和有效面积以及型钢与混凝土的粘结强度不会随时间的变化而发生较大变化。本文把混凝土的抗压强度作为随时间变化的参数来研究型钢混凝土闸墩的时变可靠度。文献[12]给出了混凝土立方体抗压强度随时间变化的均值和标准差的变化,且任意时刻的混凝土抗压强度服从正态分布。具体表达见式(3)和(4)。

式中:μfcu(t),σfcu(t)表示第 t年混凝土立方体抗压强度的均值和均方差,MPa;μfcu,0,σfcu,0表示混凝土立方体抗压强度的均值和均方差,MPa。
根据式(3)和(4)求出混凝土立方体抗压强度的平均值、标准差,再根据式(5)和式(6)转化为混凝土轴心抗压强度平均值和标准差见表3。

式中:δfcu为混凝土抗压强度的变异系数;δfc为混凝土轴心抗压强度的变异系数;δft为混凝土轴心抗拉强度的变异系数;μfc为混凝土轴心抗压强度平均值。
2.3 闸墩的目标可靠指标和承载力极限状态失效模式
目标可靠指标是规范规定结构应达到的可靠指标。本文根据《水工钢筋混凝土结构设计规范》(DL/T 5057-2009)通过校准法得到的水工钢筋混凝土结构的加权平均目标可靠指标;由于本文结构参数依据的工程的安全等级为Ⅱ级,根据规范要求其加权平均目标可靠指标β为3.7。
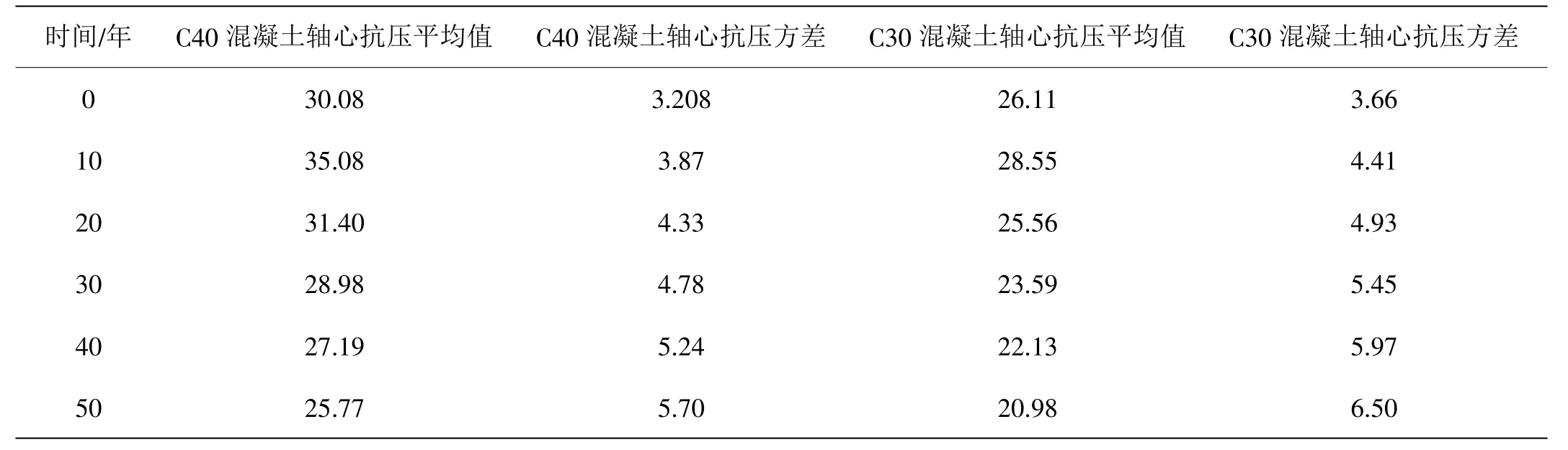
表3 混凝土抗压强度均值和标准差随时间变化 MPa
考虑到型钢混凝土闸墩的材料性能随时间不断发生变化,因此把时间当做影响结构抗力的因素,将时间作为变量。根据结构极限状态方程的定义,型钢混凝土的极限状态方程如式(7)所示。

式中:Z表示结构的功能函数;R(t)表示结构的抗力效应;S(t)则是结构的荷载效应。
型钢混凝土闸墩达到其承载极限状态主要是承受弧门推力的支座附近的型钢发生屈服和闸墩开裂出现过大的变形。由水工钢筋混凝土结构学[13]可知,当受拉钢筋进入屈服阶段,即认为结构进入破坏状态;文献[14]计算极限承载能力时,按照型钢达到屈服应力进行计算。因此,本文主要是以型钢混凝土闸墩的型钢应力失效即以型钢的最大应力达到屈服应力作为失效判据。因此上式的极限状态方程的具体形式如式(8)所示。

式中,[σ]为型钢的屈服应力,MPa;σmax为型钢混凝土闸墩在荷载作用下的型钢最大的应力,MPa。
3 闸墩时变可靠度分析
3.1 对称工况时变可靠度分析
在对称工况下,在设计基准期内每间隔10年对型钢混凝土闸墩的可靠度进行分析。限于篇幅只介绍第50年时的型钢混凝土闸墩可靠度分析。对于50年这个时间点,由于随着时间的增加,抗力也发生变化,输入参数中,混凝土抗压强度值按照表3变化,均布荷载、型钢屈服强度、型钢宽度和厚度按照表2取值,输出参数Z见式(8)。为保证结果有95%的准确性,计算时置信区间为0.95,利用响应面法得出型钢混凝土闸墩在对称工况时的响应面方程为:

根据响应面方程和表2、表3统计参数的均值、标准差以及分布类型,利用JC法计算得出可靠指标β=3.780 6,大于目标可靠指标3.7,满足可靠度要求。
为了分析型钢混凝土闸墩的型钢尺寸、型钢屈服强度、混凝土抗压强度在设计基准期第50年时对闸墩可靠度的影响,本文通过在响应面方程上进行100 000次蒙特卡罗抽样得到的灵敏度图见图5;为了进行对比,以相同方法得到闸墩刚建成时的灵敏度图见图6;在50年这个时间点上,由于抗力减小,因此,可靠指标也减小。从图6中可以看出,灵敏度图中比刚建成时增加了型钢厚度这一输入变量,表明在混凝土抗力减小时,型钢承担荷载作用增加,对闸墩可靠度的贡献增加。

图5 对称工况第50年灵敏度图

图6 对称工况刚建成时灵敏度图
对50年内的各年份依次分析,得出型钢混凝土闸墩各年可靠指标的时变可靠指标见表4。

表4 对称工况时变可靠指标
通过可靠指标的变化趋势可以看出,由于混凝土的抗力在0~10年期间略有上升,闸墩可靠度指标也稍变大,10年后型钢混凝土闸墩可靠度指标总体趋于下降,在20~30年期间下降幅度较大,因此,可以在20~30年左右进行适当维护。
3.2 非对称工况时变可靠度分析
在非对称工况下,以设计基准期第40年为例分析型钢混凝土闸墩的可靠度。选取表3中第40年混凝土抗压强度的均值和均方差为输入参数。均布荷载、型钢屈服强度、型钢宽度和厚度按照表2取值,输出参数Z见式(8)。计算时置信区间为0.95,利用响应面法得出型钢混凝土闸墩在单侧受力时的响应面方程为:

根据响应面方程和表2、表3统计参数的均值、标准差以及分布类型,利用JC法计算得出可靠指标β=4.805 4,相比于刚建成时的可靠指标β=6.596 9,可靠指标降低明显。
通过在响应面方程上进行100 000次蒙特卡罗抽样得出的40年时灵敏度图见图7,以相同方法得到闸墩刚建成时的灵敏度图见图8。从灵敏度图中可以看出,闸墩在非对称工况时,均布荷载、型钢强度、墩体C30混凝土抗压强度、牛腿处C40混凝土抗压强度、型钢厚度、型钢宽度等输入变量在设计基准期内对可靠度的敏感性均较高。在第40年时,由于混凝土抗压强度的减小以及方差变大,因此混凝土对可靠度的作用也相应减小,混凝土的承载能力减小,灵敏度图中混凝土抗压强度的敏感性也降低。
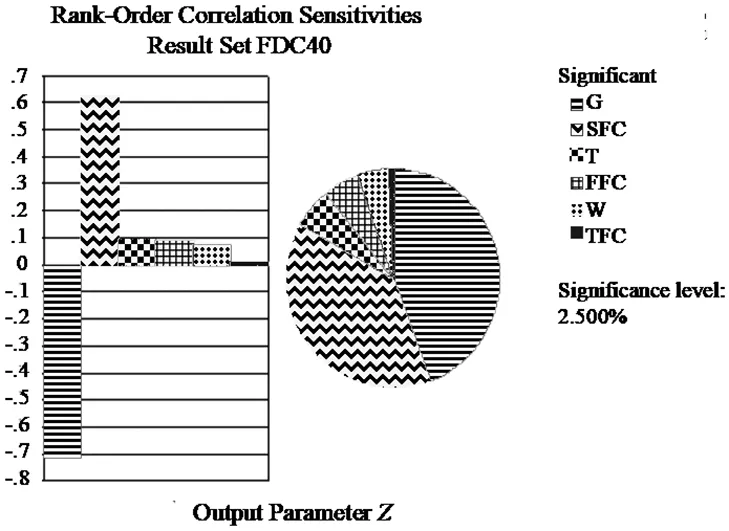
图7 非对称工况第40年灵敏度图

图8 非对称工况刚建成时灵敏度图
对各个时间段进行可靠度分析得出的可靠指标见表5。

表5 非对称工况时变可靠指标
随着时间的增加,在非对称工况下,型钢混凝土闸墩可靠指标也是先稍微增大后减小,总体呈现下降的趋势。10~20年区间下降较大,因此可以在10~20年期间进行适当维护。
4 结论
通过对型钢混凝土闸墩在设计基准期内时变可靠度的分析,得出如下结论:
(1)型钢混凝土闸墩在对称工况和非对称工况下,其可靠度的变化趋势均是先增大再减小,总体变化趋势是减少的。对于对称工况而言,闸墩在20~30年可靠指标下降较快,对于非对称工况在10~20年期间的下降幅度较大。因此,建议在10~20年期间进行适当的维护,保证其可靠度。
(2)根据设计基准期内可靠指标变化可知,对称工况在设计基准期内可靠指标下降了20.17%,非对称工况下可靠指标下降了30.07%,说明在设计基准期内,和对称工况相比,非对称工况下可靠指标降幅更大,减小的速度更快。应尽量减少闸墩在非对称工况下运行的时间。
