基于两步聚类算法的数字化数学教学资源归并分类方法

褚正清

(安徽新华学院 通识教育部，合肥 230088)

充分利用数字化教学资源，提升授课过程中课程直观性，具有开阔视野、增强学生思维能力的优势。数字化数学教学资源指针对数学课程所制定的数字化资源，学生学习数学课程时需具有较高的学习兴趣。数学课堂教学的生动性极为重要，对数学教学资源实施数字化处理，有助于提升数学教学质量。聚类算法是依据不同类别事物所存在的相似性实施分类的重要算法。聚类算法又称为点群分析，依据待分类事物间所存在的特征精准分类事物，属于多元统计的重要方法。事物间存在特征类别众多，依据事物间所存在的特征，无须先验知识即可获取分类结果[1]。聚类方法目前已广泛应用于社会学、教育学、心理学、经济学等众多领域中。

巴志超等人提出基于主题语义扩展的混合类型数字资源分类方法[2]，通过可行性分析对数字图书馆资源进行特征提取，构建语义主题模型进行数字图书馆资源语义扩展，实现数字资源自动分类。李植等人提出一种适于Docker容器资源控制的分类预测方法，通过cgroups技术进行Docker容器资源服务质量分类，利用谱聚类算法进行容器资源使用次数预测，实现有效容器资源。以上两种方法分别针对数字资源以及容器资源分类问题进行研究[2-3]，并获取较高的分类效果，但以上方法应用于数学教学资源中，分类效果较差。

为此，提出一种基于两步聚类算法的数字化数学教学资源归并分类方法。提取数字化数学教学资源特征，依据所提取特征利用两步聚类算法对资源实施归并分类。特征提取可将具有较高维度的数字化数学教学资源降低至较低维度中，依据固定变换规则，降低原始教学资源数据维数，为后续数字化数学教学资源的精准归并分类提供数据技术。通过实验验证采用该方法对数字化教学资源实施归并分类具有较高有效性，可应用于数字化教学资源归并分类实际应用中。

1 两步聚类算法的数字化数学教学资源归并分类

1.1 数字化数学教学资源特征提取

数字化数学教学资源应用过程中，随着教学课程课时增加，资源数据呈增量发展趋势。提取数字化数学教学资源特征过程中，应同时考虑新增数据以及历史数据，基于全局角度实现特征提取，避免忽略资源中所蕴含的隐藏信息。采用自适应滑动窗口互信息方法处理数字化数学教学资源的历史数据以及增量数据，实现数字化数学教学资源特征提取。

用矩阵X1=[x1,x2,…,xm]表示原始窗口数据，矩阵X2=[xm+1,xm+2,…,xm+r]表示增量窗口数据；数字化数学教学资源中所包含全部数据用X=[X1,X2]表示；Z1与Z2分别表示数字化数学教学资源原始窗口数据以及新增窗口数据的互信息矩阵；Z表示全部数字化数学教学资源样本的互信息矩阵。

依据互信息定义可得互信息矩阵表达式如下：

(1)

对角化处理利用单位阵表示Z1的特征分解公式如下：

(2)

利用G1所张成的空间接收Z2的投影，可得公式如下：

(3)

求公式(1)与公式(2)之和可得：

(4)

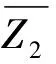
(5)

将公式(5)代入公式(4)，获取表达式如下：

(6)

通过以上过程即可获取全部数字化数学教学资源特征分解结果。

通过公式(2)可知：

(7)

公式(7)中，Λ1∈Rm×k与B1∈Rn×k分别表示数量为前k个特征值所组成的矩阵以及原始数字化数学教学资源主成分决策矩阵。

通过以上过程获取新增窗口数据互信息矩阵的特征值Λ2以及特征向量P2，且Λ2=[μ1,μ2,…,μn]，P2=[β1,β2,…,βn]。

依据特征向量以及特征值获取全部数字化数学教学资源样本特征值公式如下：

(8)

公式(8)中，m表示历史数字化数学教学资源样本数据；r表示新增数字化数学教学资源样本数据。

可得数字化数学教学资源特征向量公式如下：

P=G1βi.

(9)

利用所获取的特征向量建立主成分决策矩阵，将数字化数学教学资源映射至所建立的主成分决策矩阵即可实现数据降维[4]。后续窗口重复迭代以上过程实现全部数字化数学教学资源样本特征提取。

1.2 两步聚类算法的归并分类

两步聚类算法主要包括构建特征树以及层次凝聚算法分组两部分。

(1)构建特征树。利用所提取的数字化数学教学资源样本特征构建特征树。依据所设定固定顺序扫描数字化数学教学资源全部样本数据特征，完成扫描后确定数据类别以及不同类别中心，将待分类数字化数学教学资源依据固定标准划分至不同类别中，以上过程即建立特征树的过程[5]。所构建特征树利用叶节点根部存储数字化数学教学资源观测量，所包含变量信息均通过叶节点体现。将已存在节点以及后续观测量利用相似性测度对比，比较结果为相似时，将相似观测样本加入现有节点中；比较结果为不相似时，在特征树中建立新节点，直至全部数字化数学教学资源数据比较完成，实现特征树构建。

(2)特征树叶节点分组。选取层次凝聚算法分组所构建特征树叶节点，算法运算过程通过欧式平方距离的平方根实现连续变量测度，欧式距离度量公式：

(10)

连续变量以及分类变量的处理利用似然对数距离实现，似然对数距离是基于距离所获取的概率值。似然对数在不同类别合并为相同类别时有所降低，不同类别间距离有所变化。

连续变量以及分类变量在似然对数运算过程中需符合正态分布以及多项式分布[6]，采用似然对数距离应用于数字化数学教学资源合并与分类时，设置不同变量均为独立状态。

定义类别j与类别s间距离d(j,s)表达式如下：

d(j,s)=xj+xS-x〈j,.s〉.

(11)

公式(11)中，〈j,s〉表示通过归并处理所获取的类别。

利用BIC判据以上过程的分类运算结果，初始估计所获取分类数量。初始分类中最为相近的两种类比间，存在最大增长距离的聚类数即最终聚类数量。

用R表示聚类数量，可得最终归并分类计算公式如下：

(12)

(13)

以上公式中，HA与N分别表示归并分类过程中连续变量总数量以及观测量总数量，mj表示叶节点数量，LH与HB分别表示待分类数字化数学教学资源归并分类第k个变量编号以及归并分类过程中所采用全部分类变量总数量。

2 实例分析

选取某高校数理学院数字化数学教学资源作为实验对象，所采集数字化数学教学资源大小为5.98 GB，采用两步聚类算法的数学教学资源归并分类方法对所采集数字化数学教学资源实施归并分类，验证此方法归并分类结果。

设置数字化教学数学资源作为测试变量，采用BIC结果确定最佳分类，BIC自动聚类结果如表1所示。

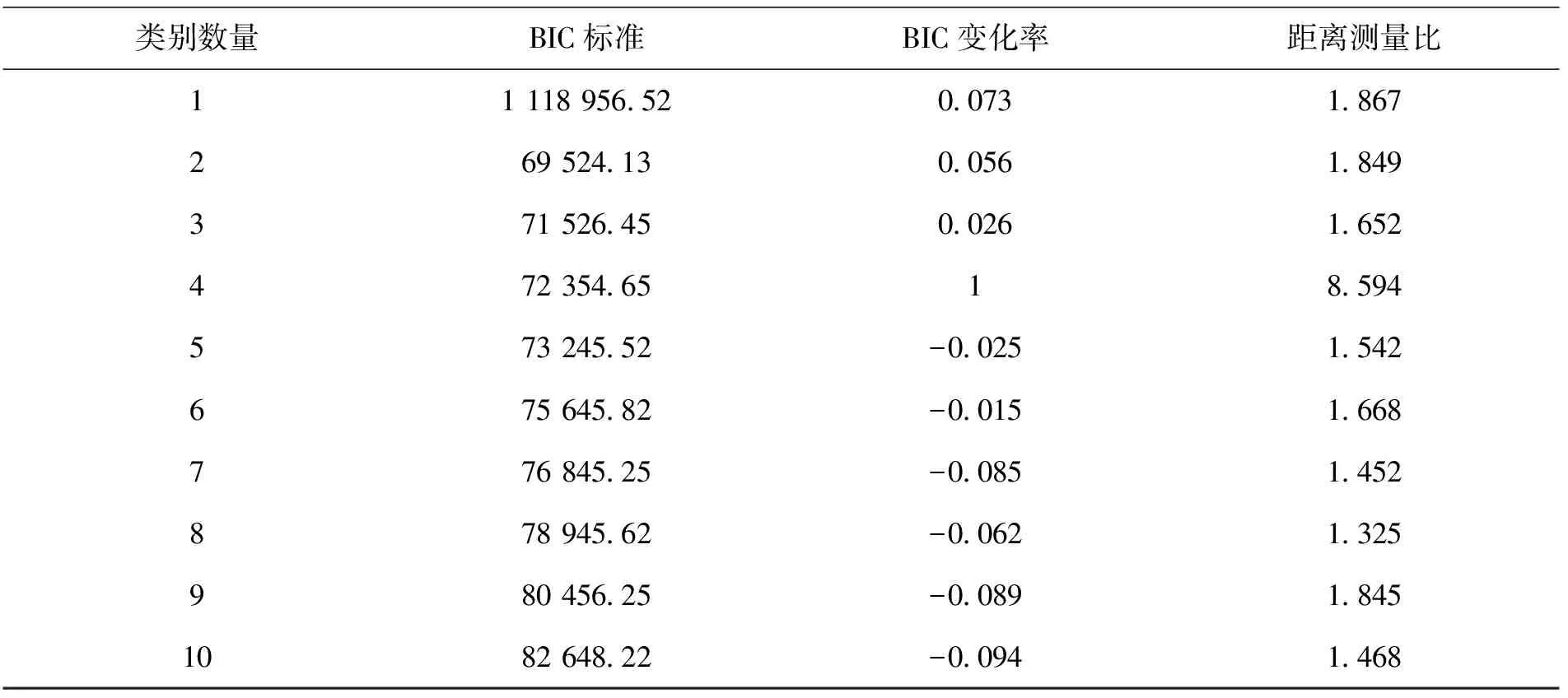
表1 自动聚类结果

通常情况下，通过聚类算法所获取的BIC值越小，表示该聚类算法聚类性能越优，所生成聚类数据质量最高。通过表1可以看出，聚类数量提升时，所获取BIC值有所降低，因此需衡量距离测量比以及BIC变化率决定最佳聚类数量。聚类测量比结果较高，且BIC变化率同样较高时，该聚类方案为最佳。表1实验结果可以看出，所获取聚类类别为4类时，通过聚类所获取聚类测量比最高，同时BIC变化率最高。因此将数字化数学教学资源分为4类。

选取文献[5]方法以及文献[6]方法作为对比方法，不同方法对数字化数学教学资源归并分类结果如表2所示。

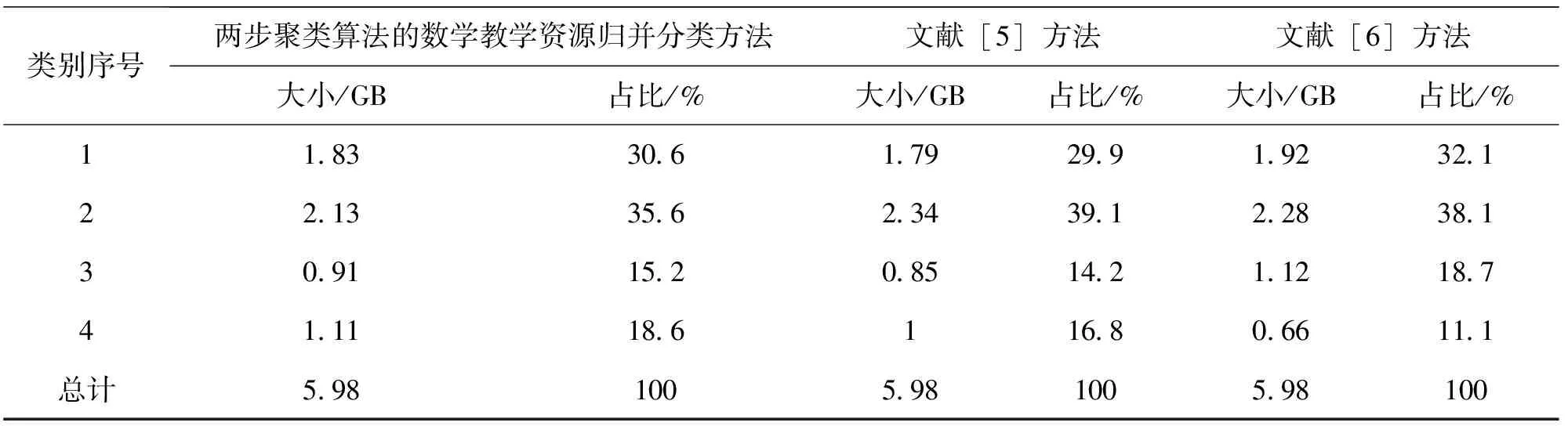
表2 不同方法归并分类结果

由表2可以看出，采用三种方法均可实现数字化数学教学资源的有效分类。采用两步聚类算法的数学教学资源归并分类方法依据BIC变化率以及距离测量比结果，将数字化数学教学资源分为4类，各类分别占总数的30.6%、35.6%、15.2%以及18.6%。

统计不同窗口大小时，三种方法对数字化数学教学资源的归并分类效率，对比结果如图1所示。

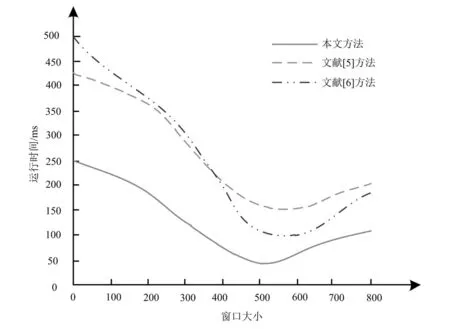
图1 窗口大小对归并分类效率的影响

由图1可以看出，不同方法归并分类数字化数学教学资源的运行时间随着窗口大小增加呈下降趋势；窗口大小高于600时，不同方法归并分类数字化数学教学资源运行时间有所提升。主要原因是运算窗口过小时，方法需从缓冲区域提取数据，占用过多时间；运行窗口大小过大时，提升了数字化数学教学资源特征分解时间。因此窗口区间处于300～600时，数字化数学教学资源归并分类效率最佳。相比于另两种方法，两步聚类算法的数学教学资源归并分类方法的归并分类效率在不同窗口大小时均为最高，说明该方法归并分类运算效率高于另两种方法。

采用常应用于归并分类中的评价指标查全度、准确度以及F1估计值评价不同方法归并数字化数学教学资源分类准确率。归并分类应用中，F1估计值高于90%时，表示该方法具有较高的归并分类效率。统计采用两步聚类算法的归并分类数字化数学教学资源的归并分类性能，统计结果如表3所示。

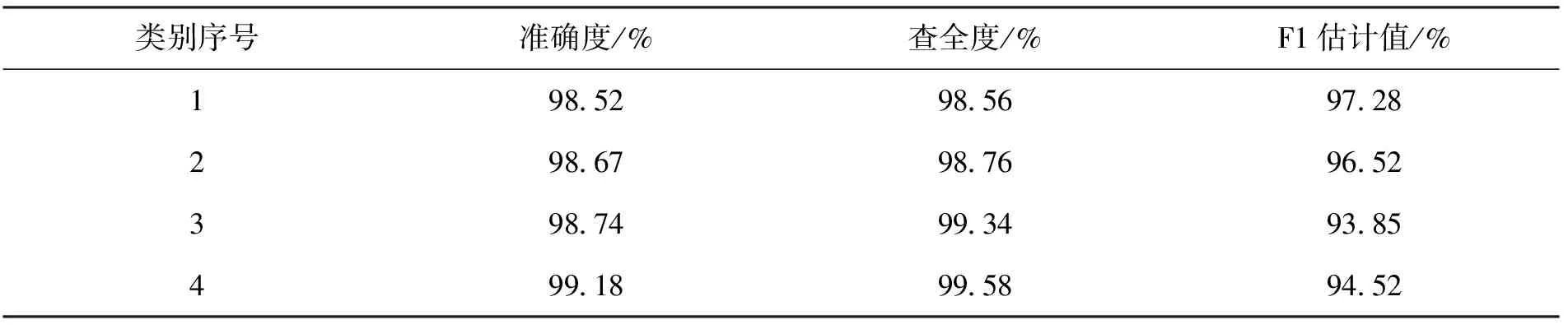
表3 归并分类性能统计结果

表3实验结果可以看出，采用两步聚类算法的归并分类数字化数学教学资源的准确度以及查全度均高于98%； F1估计值均高于93%。统计结果有效验证此方法具有较高的归并分类性能，具有较高准确率，应用性较高。

3 结论

将两步聚类算法应用于数字化数学教学资源归并分类中，利用两步聚类算法所具有的海量样本聚类性能，提升数字化数学教学资源归并分类有效性，具有优秀的运算连续变量以及离散变量能力，智能性高，具有分类严谨、操作简便的优势。①效率最高仅为250 ms。②准确率均值为98.78%，查全度均值为99.06%，F1估计均值为95.54%。

这说明所提出来的归并分类有效性较高，处理海量数字化数学教学资源时，处理可靠性高，可在数字化数学教学资源归并分类中发挥重要作用，取代以往人工归并分类的低效率方法。