一种基于支持向量机的心电信号处理算法
2021-10-05任澄飞
任澄飞,方 明
(西安石油大学 计算机学院,西安710065)
0 引 言
心电信号(Electrocardiography,ECG)是心脏病学领域中广泛采用的一种分析人体心脏状况的方法,代表心脏的电活动,广泛应用于心律失常的检测和分类[1]。人类心脏进行生理活动时,通过体表电极采集所得到的时变电位信号中,包含了丰富的生物学信息,在医学诊断和研究中具有重要意义[2]。经验丰富的心脏病专家可以通过肉眼检查心电图波形来检测心律失常。然而,心律失常在问题的早期阶段容易发生间歇,因此很难在较短的心电波形时间窗内对其进行检测。所以,日常生活中持续监测患者的心跳对心律失常的检测至关重要。
目前,对心电信号识别分类的主要方法有统计模式分类、结构分析分类法等。文献[3]中提出,通过高阶统计量的方法,将最初波形转换到3个累积量,然后利用一个基于粗糙集理论的决策表分类器进行分类,最终得到决策表的分类精度达到了90.2%。Desai等人先采用常规方法进行心电滤波和分割,然后采用离散余弦变换算法进行特征提取,使用主成分分析方法进行特征缩减,最后采用K近邻算法进行分类,最终得到的总体平均准确率为98.61%[4]。Saeed等人提出了一种基于小波变换和多个长短期记忆神经网络新的分类算法。该算法成本低,能够满足可穿戴设备上的时序要求,优于以往的算法[5]。在心电信号的识别分类流程中,主要是通过一些比较成熟的算法提取信号的关键特征值,然后通过不断优化网络参数进行训练,依据训练结果进行病理分析。在实际生活中,心电图的识别分类算法对医生只能起到辅助的作用,具体的诊断及治疗方案需由医生去实施,因而心电图的理论和算法还需进一步研究。本文在支持向量机的基础上,采用台湾大学林智仁教授开发的libsvm工作包作为分类器对ECG信号进行分类,构建出了一个基于支持向量机的心电信号处理算法,可以有效提高心电信号分类的敏感度。
1 ECG信号的预处理
心电信号是一种微弱的生理电信号,易受噪声干扰[6],因此在信号处理之前需要进行预处理。预处理的目标是消除噪声,没有噪声的波形特征看起来更单一。在心电信号中,最显著的特征值是QRS波群,看起来相对干净的信号,能够为后续特征值的提取和分类提供方便。
1.1 ECG信号预处理中自适应阈值的设计
要完成QRS波群的定位,主要通过设置自适应阈值来实现。由于心电信号是非平稳信号,在进行检测时,仅靠固定阈值难以满足所有的R波,易造成误检和漏检,而自适应更新阈值能较好地解决这个问题[7]。自适应的意思是能够自动适应不同类型的记录。自适应机制较好的算法,是能够在各种类型的记录下区分目标与非目标,从而达到很高的准确率和可用度。
1.1.1 自适应阈值的设计原则
(1)自适应阈值机制中的经验参数需固定。在自适应阈值的变化机制中,有些参数需要根据经验提前设定,对于不同的记录,已经设定好的经验参数不允许再改变。
(2)自适应阈值要随着心电信号波形即时的变化。该阈值并不是只给一整条记录计算好一个阈值后就一成不变了,而是要跟随波形实时地变化。例如,当检测到的QRS波振幅呈总体上升态势时,自适应阈值也要相应地提高,反之则要相应降低。一般可以通过设定上下限的方式来限定自适应阈值,确保该阈值变化更加稳健。
(3)想要提高自适应阈值的效率,还需要设置特定的机制,防错检、漏检。该机制主要是利用“不应期”的概念,在检测到一个QRS波后,在0.24 s内不再检出QRS波,通过回溯已经检测过的波形信号来达到防止漏检和错检的目的[8]。
1.1.2 自适应阈值的设置
(1)自适应阈值要跟随波形信号即时变化。在连续监护过程中,心电信号的幅值、形态都会随着时间发生变化,因此算法的2个检测阈值不能一直固定不变[9]。为了让阈值更加准确,采用双阈值的方法,设置一高一低2个阈值。当信号中的某个波峰超过设定的低阈值时,就判定为一个QRS波,依据高低阈值与波峰振幅之间的联系,调整阈值的大小。
(2)为了保持心电信号波形变化的稳健,阈值还需进行调整,调整的依据是之前检测到的正确波峰振幅变化,保证阈值不会太高或者太低。
综上所述,本文设计的自适应机制如式(1)、式(2)所示:

式中,THR1为高阈值;mean(peak_buffer)为峰值均值;peak为此刻检测到的信号峰值;THR1_lim为经验常数,代表阈值变化的上界,在本文中取值为0.3;THR2为低阈值;peak_buffer为存储此刻峰值之前的8个连续峰值的缓冲值;THR2_lim也为经验常数,代表阈值变化的下界,在本文中取值为0.23。
(3)防漏检与错检。设计双阈值可以在一定程度上防漏检。因为设置高、低2个阈值,相比只有一个阈值来讲,可以在很大程度上捕捉到更多层次的波峰。在防错检方面,采用了“不应期”的方式。当2个波峰距离较近时,只选取较大的波峰。这个“过近”指的是时间距离低于0.24 s,即不应期的长度;双阈值的数值存在下界,也在某种程度上防止了一些噪声被错检为QRS波。另外,双阈值的初始化参数是被提前设置好的经验系数,一旦确定就不会因记录的不同而改变。
1.2 ECG信号预处理中QRS波定位算法的设计与评估
(1)预处理总体步骤
在对心电信号预处理时,首先使用带通滤波器去除频率在15~20 HZ之间的噪声成分,采用“双斜率”方法,获得QRS波群的斜率信息后,将低通滤波器的截止频率设定为5 Hz,以滤除高于截止频率的波形,最后使用滑动窗口积分对波形信号进行平滑处理。
(2)使用“双斜率”方法预处理滤波后的波形信号。“双斜率”的基本算法思想是:在一个点左侧的某个区间内寻找最大平均斜率和最小平均斜率,然后在这个点的右侧的某个区间内寻找最大平均斜率和最小平均斜率,即可得到4个斜率值,接着求左侧最大平均斜率与右侧最小平均斜率之差,求右侧最大平均斜率与左侧最小平均斜率之差,最后再求两个差值中的最大值[10]。“双斜率”基本思想主要在于QRS波群的宽度相对固定[11],其基本动机主要利用QRS波两侧较陡的性质,其尖峰在经过双斜率处理时会有很大的响应,一般设置寻找斜率的区间是左右两侧0.015~0.060 s处为经验参数。
(3)滑动窗口积分。心电信号的波形由于受到滤波或是求斜率的影响,其幅度值会越来越小,而过小的幅值其实不利于检测,利用滑动窗口积分[12],会让绝对振幅的值变大,波形更加光滑,本文中设置滑动窗口宽度为17个采样点的经验参数。
2 基于支持向量机的心律失常识别
2.1 基本概念
2.2 心律失常识别过程
2.2.1 SVM算法原理
(1)线性不可分问题
在现实应用中,样本一般都是线性不可分的问题,对于给定的样本集:
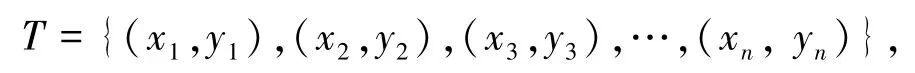
其中,yi∈Y={+1,-1}表示类标记,分别用+1和-1表示,分别对应正样本和负样本。支持向量机最终的优化问题可以转化为:

其中,x为输入向量;w是权重向量;b是偏置项;ξi是松弛变量;C为惩罚因子。
(2)对偶问题
由于上面的优化问题带有大量不等式约束,不易求解,因而使用拉格朗日函数,将其转化为对偶问题。构造拉格朗日函数:
事情过去两天后,项目部副经理开始找我谈话。主题是我在这件事情上欠考虑,影响了正常的生产工作。我脑子热的已经冷静不下来了,心里倍感委屈,觉得自己并未做错什么,冷冷地甩下两句话:“我履行了自己的职责,处罚通报也是经你们同意的,如果你不满意我的工作,可以换人。”随后夺门而出。接下来的几天时间里,我完全没有工作的心,每天就在办公室做做资料,浏览一下网页,再也没去现场。
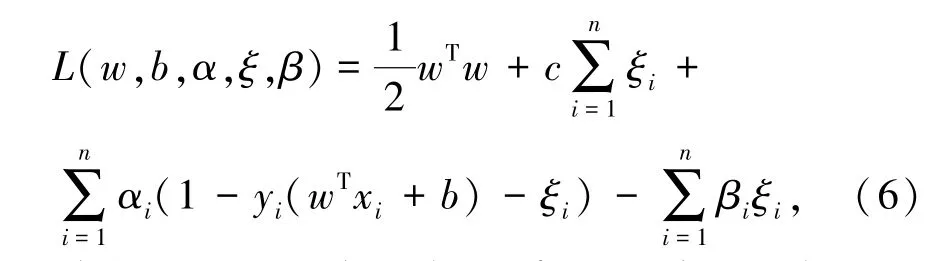
其中,α和β是拉格朗日乘子,为求得对偶问题的解,即求:
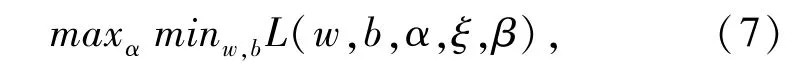
求拉格朗日函数的极小值,则对w、b、ξ求偏导数,并令其都为0。将w代回拉格朗日函数中,消除w和b,即可得到关于α和β的函数。经过一系列转化后,等价于最大化函数为:
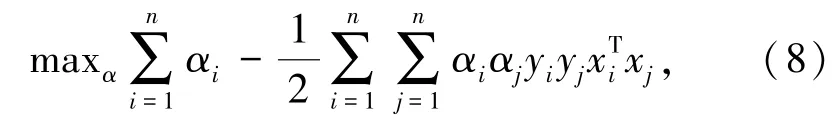
其约束条件为:
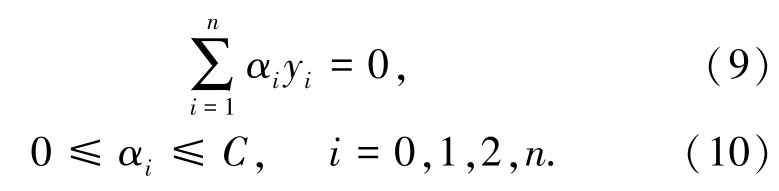
(3)核函数
虽然加入松弛变量和惩罚因子后可以处理线性不可分问题,但支持向量机还是一个线性分类器,只是允许错分样本的存在。因此,引入核函数使得支持向量机成为非线性分类器,决策边界不再是线性的超平面,而是形状非常复杂的曲面,从而可以将样本从原始空间映射到更高维度的特征空间,使问题得到有效地处理。
假设φ(x)为映射后的特征向量,则在该特征空间上的讨论模型即可变为:
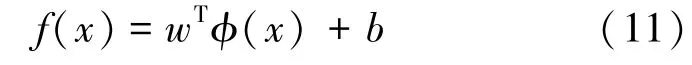
同样求得对偶问题:
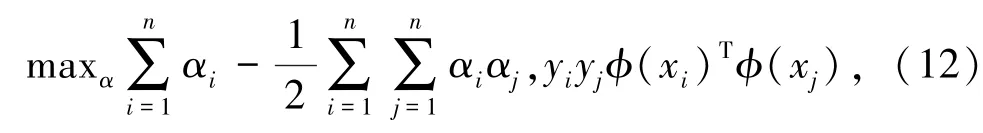
也就是求解:

约束条件为:

假设核函数:
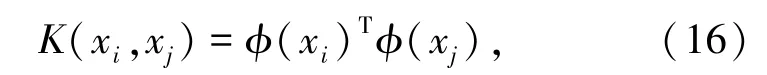
于是可以解得:
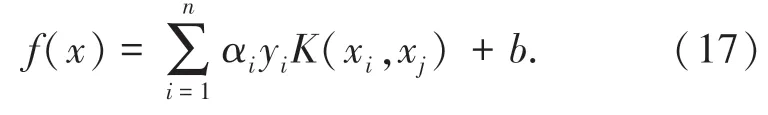
常见的核函数有线性核、多项式核、高斯核、sigmoid核等。
2.2.2 基于SVM在心电信号中的应用
(1)心电信号特征提取。首先加载ECG信号数据集,然后对数据集中的每个心拍进行5阶的小波分解,小波函数利用db6小波[14]。经过5阶小波分解和2倍下采样后,取小波变换系数中原信号的“近似”系数,即5阶分解后的a系数,选取这些系数作为每个心拍的特征值。
(2)数据集选取与划分。对于数据集,随机划分训练集和测试集,即训练集和测试集各有10 000个样本。随机选取可通过立建randperm函数随机打乱样本索引,然后截取前10 000个索引对应的样本作为训练集,剩余的作为测试集来实现。
(3)特征归一化。为了加快SVM的收敛,对数据进行了特征归一化处理。实际操作时,先使用归一化函数的正常模式,对训练集特征归一化到0~1之间,得到归一化后的训练集和归一化信息后,使用归一化函数的apply模式,将训练集得到的归一化信息应用至测试集,完成测试集的归一化。
(4)模型训练与测试。调用libsvmtrain函数和libsvmpredict函数训练和测试模型。libsvmtrain函数训练的默认核函数为RBF核函数,需要人为设定2个超参数——惩罚因子系数c和核函数参数g,分别将其设定为2和1。不同取值的c和g可能会导致差异较大的结果,如果想要取得更好的效果,必须进行“调参”,减轻欠拟合与过拟合问题。常用的调参方法除了手动调整,还有网格搜索、随机搜索、启发式寻优等方法[15]。
3 实验结果与分析
3.1 数据来源
本实验使用的心电信号均来自于MIT-BIH Arrhythmia Database数据库。该数据库是PhysioBank项目的子数据库,是一套用于评估心律失常检测器的通用标准测试数据。其中包括48条双导联ECG记录,约65万个采样点。实验平台为Core i7-8700、8GB内存的64位Windows10操作系统;代码基于matlab语言编写,每条记录对应3个文件:
(1).atr标记文件。记录人工标注的心拍位置和类型,格式为二进制数。
(2).dat:数据文件。记录所需要的心电信号。
(3).hea头文件。存储记录的附加信息。如,记录编号、信号通道、导联数、采样率、采样点数、文件的格式编码等。
3.2 实验结果
首先读取了编号为100的记录,指定读取的点数为1024,绘制出的2个导联的信号如图1所示。在命令行输入plot(M(:,1));grid on;之后即可单独绘制出第一个导联的信号图,如图2所示。
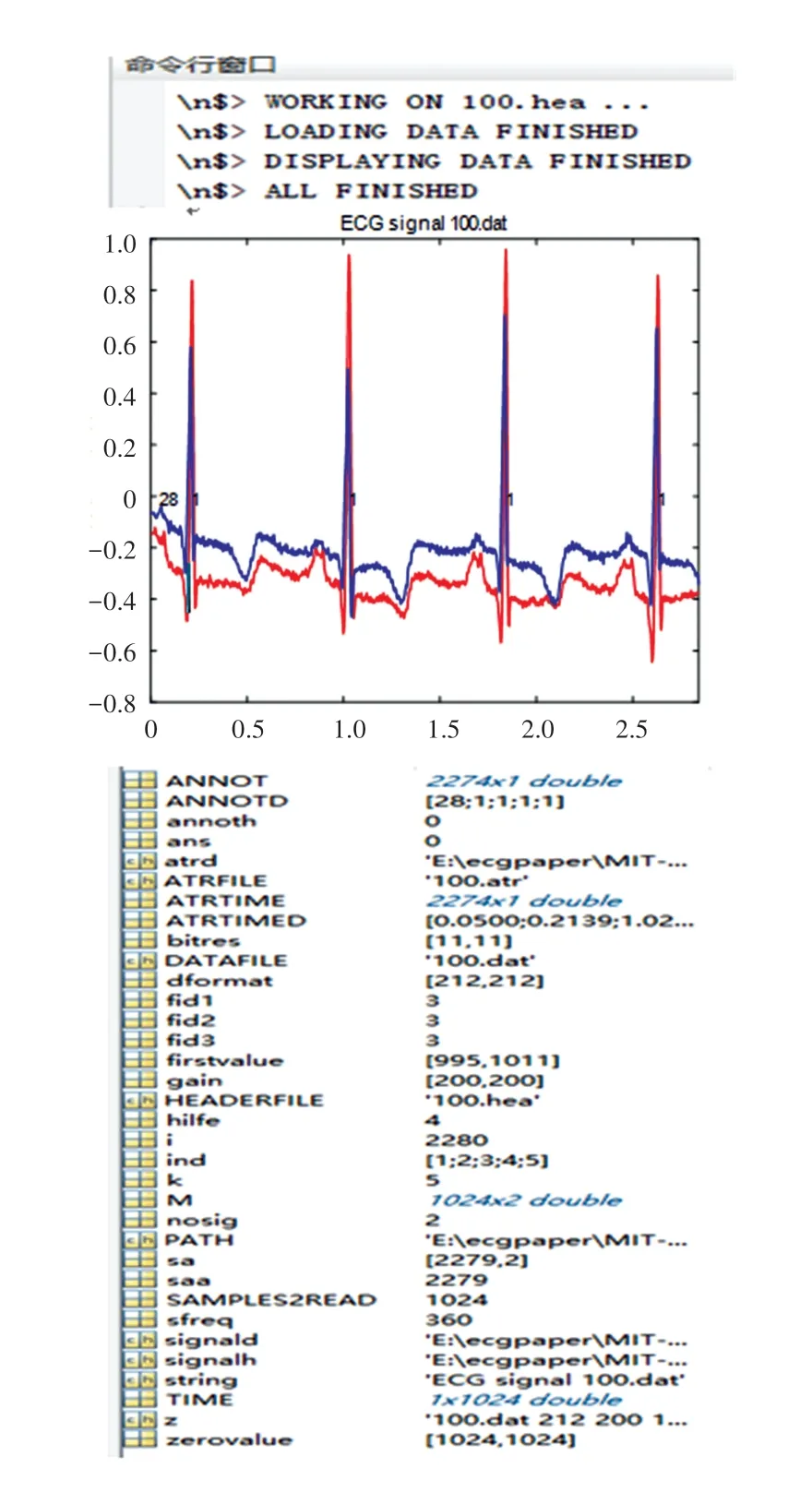
图1 记录号为100的心电信号Fig.1 ECG signal recorded as 100

图2 第一个导联的信号Fig.2 Signal diagram of the first lead
经过双斜率处理后,波形模式更为单一,QRS波的变化更为突出。但是,心电信号波形出现了双峰现象,从某个角度来看,检测的精准度不够高。
因此在双斜率处理之后,须采用低通滤波方法以使波形变得非常光滑,杂波基本消失,模式也非常单一,基本上达到了进一步阈值处理的要求。
滑动窗口积分后的波形如图3所示。

图3 滑动窗口积分后波形图Fig.3 Waveform after sliding window integration
3.3 算法评估
为了评估所提出方法的性能,采用QRS波检测算法的2个惯用指标:敏感度(Sensitivity,SE)和正预测率(P+)。其敏感度和正预测率指标定义如下:

其中,TP(true positive,TP)代表正样本中被分类器判定为正确的心拍个数;FP(false positive,FP)代表检测错误的心拍个数;FN(false negative,FN)代表正样本中被分类器检测为漏检的心拍个数。对整个数据库的实验结果见表1。
从表1中可以看出,共错检出648个心拍,漏检了380个心拍,总体Se达到了99.65%,P+达到了99.41%。

表1 数据库的实验结果Tab.1 Database experiment results
经典的pan_tompkin算法开发了一种QRS波群检测算法。该算法采用了带通滤波器,利用坡度、振幅和宽度检测了QRS波群,最终检测的正预测率达到了99.3%。而本文不仅采用了自适应阈值算法、双斜率算法,还设置了漏检和错检机制,最终检测到的正预测率为99.38%。本文实现的算法与经典的pan_tompkin的99.3%相比,正预测率提高了约0.08%,具有较高的准确率和可用度。
3.4 基于支持向量机的算法的分类结果统计
基于高效的QRS波算法,本文采用支持向量机对心电信号进行了分类。经过特征提取、选取与划分数据集、特征归一化、训练与测试等操作后,可以看出:在本次实验中,SVM模型的总体预测准确率为96.69%。其中4类目标类型的准确率分别为:正常(N)99.68%,室性早搏(V)90.90%,右束支阻滞(R)97.58%,左束支阻滞(L)98.49%.
4 结束语
本文通过对MIT-BIH数据库进行预处理后,使用自适应阈值对心电信号进行波形处理,最后使用敏感度以及正预测率对算法进行了评估,实验表明其结果优于传统的pan_tompkin算法。总体而言,本文提出的算法为心电信号的预处理和精确特征提取进行了拓展。在未来的工作中,还需要进一步改进算法,减少计算时间,提高鲁棒性。
