基于不变量的机器学习算法分析

宁一璇

(浙江理工大学 信息学院，杭州311121)

0 引 言

近年来，人工智能与机器学习技术已经越来越成熟，已经渗透到人们生活的方方面面。例如，图像识别、无人驾驶等领域。伴随着智能技术的发展，人们对于机器学习程序高质量的需求日益增加，但现阶段对机器学习算法的分析与理解不足，并且传统的软件测试方法和评价标准也并不适用机器学习算法［1］。如何分析机器学习算法，已成为亟待解决的问题。

目前对机器学习进行质量分析，主要集中在以下几种方法:

（1）提高数据集质量。如Chakarov等人［2］提出PSI工具。认为对于分类任务，训练集中的错误会导致大量的分类错误。

（2）测试训练好的模型。如Groce等［3］提出了WYSIWYT／ML框架，帮助终端用户测试机器学习系统。

（3）利用蜕变测试方法，来测试机器学习程序代码。如Xie等人［4］尝试用蜕变测试来进行机器学习程序的测试。但从算法上对机器学习进行质量分析的研究甚少。

程序不变量常被用于追踪软件缺陷［5］、硬件错误［6］和软件评估［7］。在程序运行时，能够反映程序代码在整个运行过程中，具有不变性质的逻辑断言。不仅如此，还可以反映程序数据结构等各方面的信息，在程序的设计、测试等各方面都发挥着巨大的作用［8］。因此，可以将程序不变量用于机器学习算法的质量分析。

基于此，本文提出了基于不变量的机器学习算法分析。该分析方法将程序不变量与关键变量筛选提取方法相结合，通过对不同参数输入下的机器学习算法进行程序不变量的生成，然后对生成得到的不变量集合进行关键变量的提取，进而对机器学习算法进行分析。本文使用5种机器学习算法作为示例算法，并对每个示例算法选取一种对算法性能产生影响的参数作为输入。实验结果表明，本文提出的方法可以从算法内部的属性特点，分析机器学习算法的参数设置对算法准确率的影响。

1 方法概述

1.1 问题描述

通常的软件测试方法，是通过执行测试用例集来发现程序源代码中的错误。但机器学习算法与普通的代码不同，其输出是没有对错之分的，只有一个更适合于某个问题（数据集）的模型。机器学习算法的好坏程度，需要从正确率、时间空间复杂度以及数据集大小对算法效率的影响等几个方面去比较分析［9］。若要保证算法结果的正确性，最重要的是:算法推导的正确性、算法效果的正确性以及算法应用的正确性。总而言之，仅用软件测试的方法考虑机器学习是不充分的，应该从统计理论的角度，去分析一个机器学习算法是否优秀，是否有足够高的正确率。

软件分析技术可以应用在开发阶段、维护阶段以及复用阶段。文献［10］中，将软件分析定义为:对软件进行人工或者自动分析，以验证、确认或发现软件性质（或规约、约束）的过程或活动。软件分析技术分为静态分析与动态分析技术。

静态与动态分析技术的一个基本过程如图1所示。

图1 静态分析与动态分析的基本过程Fig.1 The basic process of static analysis and dynamic analysis

在软件分析技术中，程序不变量检测技术是一种将静态分析和动态监测相结合的有效分析方法。程序不变量是影响软件质量的要素之一，其在程序运行的整个过程中，反映了程序代码具有不变性质的逻辑语句。不但能表现代码的各种属性特点，还能够反映程序数据结构等各方面的信息［10］。

在程序开发过程中，程序不变量检测技术已经开始被人们广泛应用。程序不变量可以作为断言插入到程序中，保证程序在进一步测试时随着代码的变化不被改变；可以过滤失效测试用例、验证并改进测试套件、检测软件缺陷并对软件进行精确的错误定位；可以检测程序是否发生并发错误［11，14］等等。

因此，对于机器学习算法来说，可以应用程序不变量检测技术，从算法内部的逻辑属性，来分析机器学习算法是否拥有足够高的正确率。

1.2 方法提出

本文方法的实现步骤以及工作流程如图2所示。其中最重要的2个步骤分别是生成不变量与关键变量筛选。

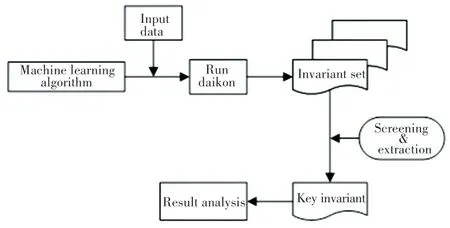
图2 基于不变量的机器学习算法分析流程图Fig.2 The flow chart of machine learning algorithm analysis based on invariants

1.2.1 Daikon生成不变量

Daikon［13］是一个应用十分广泛的不变量生成工具，其通过程序的动态运行来产生可能的不变量，可以对Java、C和C++等程序语言生成程序不变量。其产生不变量的过程如图3所示。

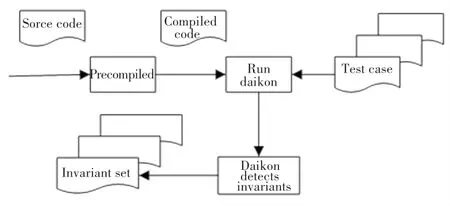
图3 Daikon处理流程图Fig.3 Daikon processing flowchart

Daikon利用机器学习的原理，使用前端对程序注入特定的程序监测点，动态分析运行程序后，得到相应的数据轨迹文件（数据轨迹即为变量的行为，它反映了程序变量之间的关系），分析数据轨迹文件便能得到程序不变量。例如，本文使用一个名为Kvasir的前端对c++机器学习代码生成数据轨迹文件，然后Daikon对数据轨迹文件进行处理，从数据轨迹文件中动态提取似然不变量，这些似然不变量在程序的某一或几个特定的程序监测点上保持成立［11-14］。

1.2.2 关键变量筛选

尽管程序不变量是观察代码内部逻辑关系、检测错误的有效方法，但由于机器学习算法是智能算法，运行时需要巨大的开销，且其中产生的不变量过于庞大，而对系统中每个变量的监控是不必要的。基于此，本文提出了对关键变量进行筛选。在关键变量筛选阶段，首先采用动态过滤机制Ⅰ和动态过滤机制Ⅱ，对成功执行程序后得到的所有变量进行过滤，得到一个关键变量集合［15］；然后使用静态约简机制，对关键变量集合进行进一步的约简；最后从约简的关键变量集合中，手动对算法正确性产生最大影响的关键变量提取。

1.2.2.1 动态过滤机制Ⅰ

动态过滤机制Ⅰ可以过滤第一类非关键变量。在程序分析阶段，这类非关键变量并不会随着参数的改变，对程序的结果产生关键的影响，因此不需要被监控。文中使用增量△来表示变量值的增加或减少。△是通过当前观察值减去上一次的观察值来获得的［16］，如式（1）、式（2）所示。

△:＝CurrentValue-LastValue if LastValue≠Ø，（1）

△:＝0if LastValue＝Ø.（2）

动态过滤机制Ⅰ可以过滤掉第一类非关键变量，并将筛选出的关键变量储存到集合KEY1中。动态过滤机制Ⅰ在训练阶段的处理过程如下:

（1）当观察到第一个值Obersvation1时，给△赋值为0，最后一个值Last＿Observation更新为第一个值Obersvation1。

（2）在 下 一 次 观 察 时，将 新 观 察 到 的 值Obersvation2和最后一个值Last＿Observation之差更新为△。

（3）每次观察后，生成一个更新的△（△2），并将其与当前△进行比较。若新△等于当前的△，则继续进行判断，否则将保存一个false标志，并将该变量的信息储存到集合KEY1中。

（4）退出训练过程，并返回关键变量集合KEY1。

1.2.2.2 动态过滤机制Ⅱ

使用动态过滤机制Ⅱ的目的，是从关键变量集合KEY1中再次过滤掉对算法的结果不产生影响、不需要被监控的非关键变量。动态过滤机制Ⅱ从关键变量集合KEY1中过滤掉这类非关键变量后，将剩余的关键变量储存到新的关键变量集合KEY2中。动态过滤机制Ⅱ在训练阶段的处理过程如下:

（1）在程序第一次执行期间，范围不变量Range＿Invariable会随着给定变量的每次观察而不断更新，并将其范围赋值给最新的Last＿Range＿Invariable。

（2）在下一次成功执行后，得到新的范围不变量观察值Range＿Invariable。判断新的Range＿Invariable是否在上一次执行得到的Last＿Range＿Invariable范围内。若在范围内，则继续进行下一次执行；否则保存一个false标志，并将该变量的信息储存到集合KEY2中。

（3）退出训练，并得到一个更新的关键变量集合KEY2。

1.2.2.3 静态约简机制

静态约简机制是通过分析函数之间的调用关系，对KEY2集合中的关键变量进一步的过滤约简，并得到新的关键变量集合KEY3。

函数调用图可以描述一个程序中各个函数之间的调用关系［17］。一般来说，函数调用图可以分为静态函数调用图和动态函数调用图两类，静态函数调用图展示了程序在不运行状态下的函数调用情况，而动态函数调用图记录了程序运行时的函数调用情况。在本文中，使用工具Cflow和Graphviz，构建静态函数调用图。例如，本文利用遗传算法，解决TSP问题的tsp.cpp程序的静态函数调用图如图4所示。

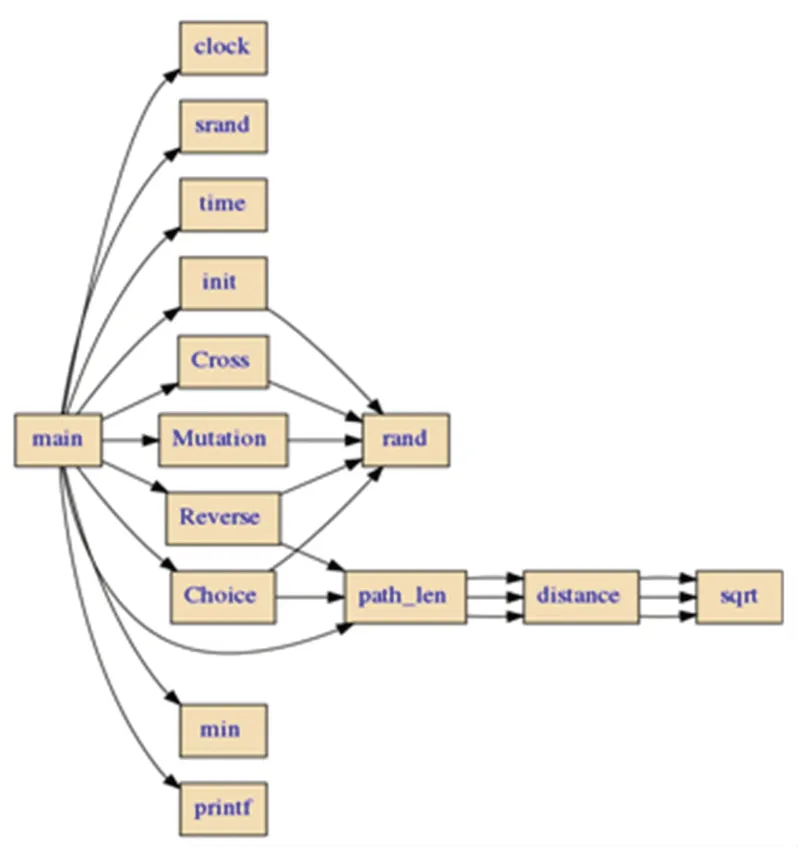
图4 GA-tsp.cpp程序的函数调用图Fig.4 Function call graph of GA-tsp.cpp program

1.2.2.4 关键变量提取

使用2个动态过滤机制和静态约简机制对程序中的变量进行过滤后，得到了一个关键变量集合KEY3。通过运行程序，调整程序运行时的输入参数。在KEY3中发现，随着参数的改变，将有一个变量会产生明显的变化，而这个变量在程序中也与欧氏距离有着直接的关系，则定义这个变量为关键变量，并对其进行提取分析。

2 实验与分析

实验中共有5个机器算法程序，见表1。

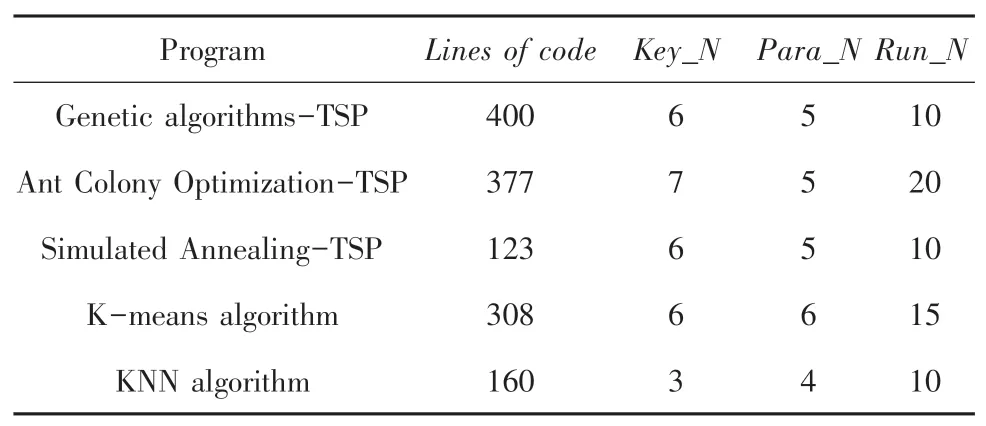
表1 5种机器学习算法参数表Tab.1 5 machine learning algorithms

其中，Key＿N表示每个程序关键变量集合中关键变量的个数；Para＿N表示每个程序所取参数的个数；Run＿N表示每个参数运行次数。

2.1 遗传算法

本文使用的第一个程序，是用遗传算法求解TSP问题（Traveling Salesman Problem，旅行商问题）。

旅行商问题（TSP）是引起数学家和计算机科学家广泛关注的一个问题，特别是因为其描述起来既容易又难以解决。问题简单地表述为:如果一个旅行推销员希望一次访问m个城市列表中的每个城市一次（从i到j的旅行成本为cij），然后返回家乡，那么旅行推销员如何选择最短的路径［18］。

以规模较小的城市为例（这里取14个）。其中，种群数目sizepop＝100；交叉概率pc＝0.8；变异概率pm＝0.02；染色体长度（即城市个数）Lenchrom＝14。选择最大进化代数maxgen为可变参数，并取20、40、60、80、100这5种参数和14个城市坐标作为输入。首先，对最大进化代数为20的程序进行不变量生成，以14个城市的坐标点为输入。通过2次动态筛选机制和静态筛选机制，过滤掉了一些非关键变量，并得到关键变量集合见表2。

表2 GA-TSP中关键变量集合Tab.2 Collection of key variables in GA-TSP

接下来，对表2中的关键变量集合进行关键变量提取，提取出main（）:::EXIT程序点中的关键变量::min＿distance进行对比分析。由已经生成的主函数调用图4中可以发现，关键变量::min＿distance是用欧式距离定义的变量。

得到关键变量后，需对其它4个参数（最大进化代数为40、60、80、100）的程序进行不变量的生成和关键变量::min＿distance的提取。由于遗传算法每次运行得到的结果波动较大，因此对每一个参数都进行10次运行和关键变量的筛选与提取，并做了平均数比较。如图5所示，图中横轴是每个参数运行的次数，纵轴是关键变量::min＿distance的大小。从图中可知，随着参数的变化，即最大进化代数的增大，::min＿distance逐渐趋于稳定，不会轻易产生较大的结果波动，也不会轻易地陷入局部最优解。如图6所示，在做了平均值对比后，随着参数（最大进化代数）的增大，::min＿distance是一个持续减小的过程，更加说明了机器学习算法的正确率与稳定性，会随着参数的变化越来越好，从而印证了该方法的可行性。

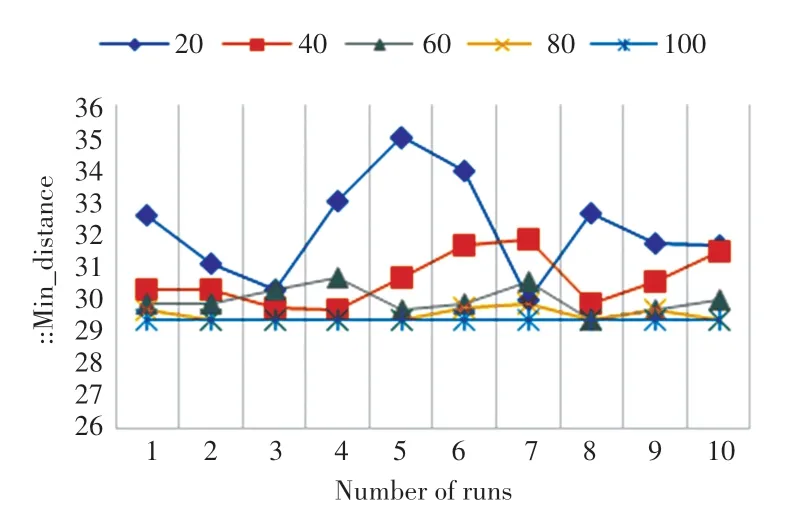
图5 每个参数运行10次Fig.5 Run 10 times for each parameter

图6 不同参数的关键变量Fig.6 Key variables for different parameters

2.2 蚁群算法

本文使用的第二个程序，是以蚁群系统为模型的蚁群算法程序（非蚂蚁周模型），并以TSP问题为测试对象。蚁群算法是一种基于种群的启发式随机搜索算法，具有正反馈、鲁棒性、并行性等优点，可以使用蚁群算法解决最短路径问题。在计算最短路径时，使用最近邻方法是从源节点出发，每次选择一个距离最短的点来遍历所有的节点得到的路径（距离可以用欧式距离公式来表示）。但蚁群算法在计算两节间的最短距离时易陷入局部最优，且随着算法复杂程度的增加其收敛速度慢，还有可能出现停滞现象。

在蚁群算法中，主要有6个参数:信息启发因子α，期望启发因子β，全局信息素挥发参数ρ，局部信息素挥发参数α1，蚂蚁数量M，以及最大循环次数NcMax。本实验探究最大循环次数NcMax与蚁群算法性能之间的关系。函数调用如图7所示。

图7 ACO-tsp.cpp程序的函数调用图Fig.7 Function call graph of ACO-tsp.cpp program

通过2次关键变量筛选机制和关键变量提取，得到直接反应欧氏距离的关键变量::Lnn。对每个参数进行20次运行和关键变量的筛选与提取，并做了平均数比较，结果如图8所示。得到的关键变量集合见表3。

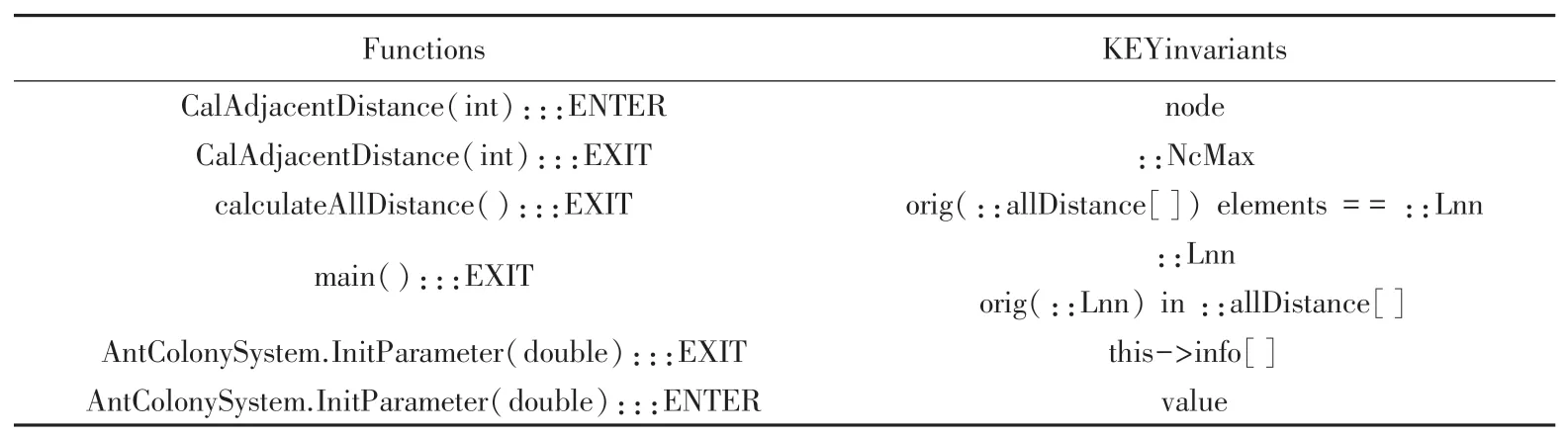
表3 ACO-TSP中关键变量集合Tab.3 Set of key variables in ACO-TSP

由图8可知，最大循环次数NcMax对算法的正确性以及稳定性有较大影响，可以直接从与欧氏距离相关的关键变量中反映出来。当循环次数越大，蚁群算法的性能越好，也越稳定。

2.3 模拟退火算法

本文使用的第三个程序，是用模拟退火算法解决TSP问题。该问题给定平面上10个点的名称与坐标，2点之间的距离为其欧几里得距离。求一条路径，刚好经过每个点一次，使其路径长度最短。

模拟退火算法是一种基于自身退火原理的随机搜索算法，其准确率与最优解的精度主要与退火速率Δ、初始温度T、终止温度e、以及循环代数L有关。根据实验可得:当循环代数L越大时，与欧几里得距离直接相关的关键变量this-＞loc＿distance和this-＞min＿distance越来越小，模拟退火算法越能跳出局部最优解，得到最短路径。关键变量集合与实验结果见表4和图9所示。

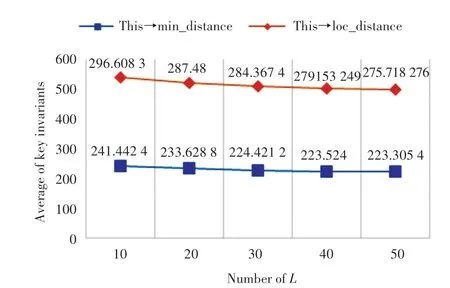
图9 不同参数的关键变量Fig.9 Key variables of different parameters

表4 SA-TSP中关键变量集合Tab.4 Set of key variables in SA-TSP

2.4 K-means聚类算法

第四个示例程序，是一个K-means聚类算法实现。输入数据集为所有点的集合，是一个二维矩阵。给定k值，将数据集中的所有点分为k类，计算k个中心点（质心）、每个点所属的归类以及距离值。其中，每个点与质心的距离由欧氏距离定义与计算。如图10所示，取k＝｛2，3，4，5，6｝后发现，当k值越大时，聚类效果越好。

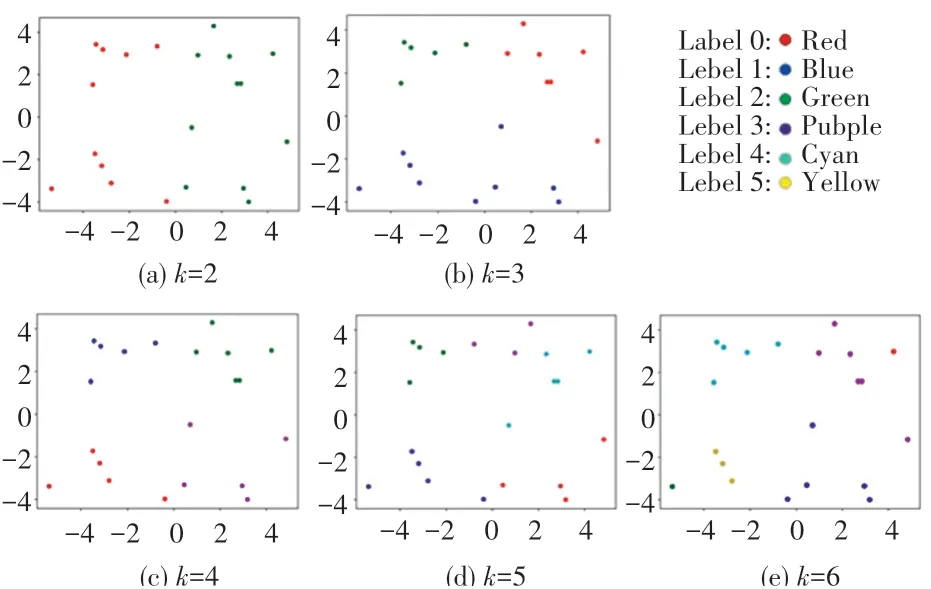
图10 k-means聚类结果Fig.10 K-means clustering results

从不变量角度看，取k＝｛2，3，4，5，6｝后，会产生｛2，3，4，5，6｝个类别。每个类别里，质心与归类的每个点之间的欧氏距离，即关键变量＿＿first［］.minDist会越来越小，如图11所示。关键变量集合见表5。

图11 关键变量趋势图Fig.11 Trend chart of key variables

表5 k-means中关键变量集合Tab.5 Set of key variables in k-means

2.5 KNN分类算法

第五个示例程序假设了一个场景，用KNN分类算法为坐标上的点进行分类，如图12所示。由图所见，共提供13个坐标点，每个坐标点都有相应的坐标（x，y）以及其所属的类别A或B。现给定一个点坐标（1.5，-0.5），判断其属于类别A或类别B。对于KNN分类算法:参数k是指选择样本数据中前k个最相似数据；计算待分类点与已知类别点之间的欧氏距离；选择k个最相似数据中出现次数最多的分类，作为测试数据的分类。

图12 KNN示例程序Fig.12 KNN sample program

本次示例中选取k＝｛3，5，7，9｝。经过不变量的生成和关键变量的筛选与提取后，可以发现，前k个欧式距离最短的关键变量在分类中起着决定性的作用。而随着k的增大，最相似数据的数量不断增大，欧式距离最短的关键变量所代表的数据标签出现的可能性也会越来越大，这时分类结果也会更加的准确。关键变量集合见表6，其中:distance即为该实例程序中与欧氏距离直接相关的关键变量。

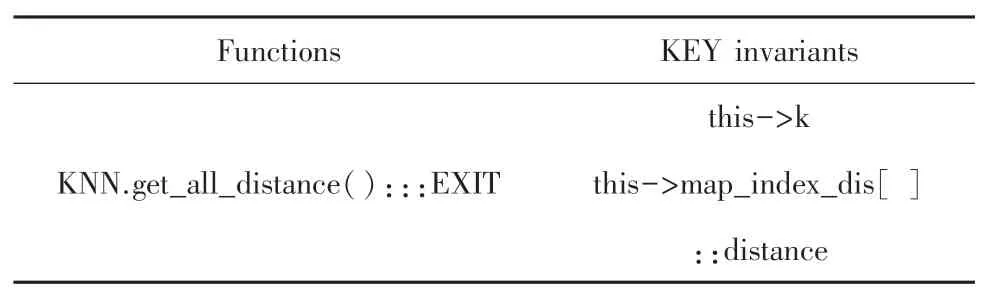
表6 KNN中关键变量集合Tab.6 Set of key variables in KNN

3 结束语

本文提出了一种基于不变量的机器学习算法分析方法。通过改变算法的参数，得到不同参数下的关键变量并分析其变化。可以得出:当机器学习算法的准确性，随着参数的调整越来越好时，基于欧氏距离的关键变量总会以一种特定的规律变化。使用静态分析加动态分析的方法，从程序不变量的角度初步探索了机器学习算法的质量，验证了对应算法的鲁棒性；探索了机器学习算法中的不变量，有别于普通程序和并发程序的不变量；机器学习算法中的不变量数量庞大，并且具有很大的不稳定性，需要进行反复多次的实验和变量的筛选。

进一步的研究将把本文方法扩展到更大、更复杂的机器学习算法中，改进关键变量的筛选机制，研究是否有更多的关键变量对算法正确率有影响，以及不同的算法与关键变量之间的关系。希望可以通过除Daikon以外其它的工具来生成不变量。此外，需要改进和研究的方面主要包括:开发一种方法来获得更加完整的关键变量集合；在更庞大、更复杂的机器学习算法上进行实验验证。