准确把握习题关键点 多维提升数学思考力

张育丽

（福建省厦门市第六中学）

在教学中我发现，有些学生只会跟着教师的节奏走，只懂得教师讲过的类型题，不懂得如何灵活运用这些类型题里所涵盖的知识解决新问题。为什么会出现这样现象？其原因是多方面的，而不会对问题进行全面分析与思考是其中的重要原因之一。要解决这个问题，教师需要注意以下三点：一是使学生获得系统的数学知识，二是掌握解决实际问题的技能，三是注意培养学生的思维能力。要教会学生思考问题的方法，使学生形成数学意识。

《义务教育数学课程标准（2011 年版）》提出的十大核心概念基本上是融合在数学思考内容里的，这充分体现了培养学生思考问题方法的重要性。让学生更好地思考数学问题，这是数学教学中的一门艺术，其方法与形式是多种多样的，学生思考问题的质量如何，反映了其数学素质的一个重要方面。在教学过程中，教师既要鼓励学生勤于思考，还要引导他们善于思考，教给他们一些思考问题的方法。数学思考的培养应该融合于知识与技能、解决问题之中，侵润于数学课堂教学的每一个环节中。

一、依托例题寻找最佳途径，快捷解决问题

在讲解例题时，应着重分析为什么这样做，而不是只满足让学生知道怎么做。特别是讲解几何证明题时，教师要讲清证明思路，让学生知道为什么这样做，这种方法是如何想出来的，为什么会这样想，为什么不是从其他方面想，若从其他方面想，又可能会产生什么样结果。思考问题的方法是数学的核心和灵魂，只有掌握了正确的数学方法，才能在看似错综复杂的数学问题前从容不迫，得心应手，并且进行深入地探索与研究。正如著名数学家笛卡尔说的那样：“没有正确的方法，即使有眼睛的博学者也会像没有眼睛一样盲目摸索。”由此可见，把思考问题的方法教给学生，进而选择恰当的数学方法进行解题是至关重要的。

如图1，AE是ΔABC的外接圆O的直径，AD⊥BC于D。求证:ΔADC～ΔABE。

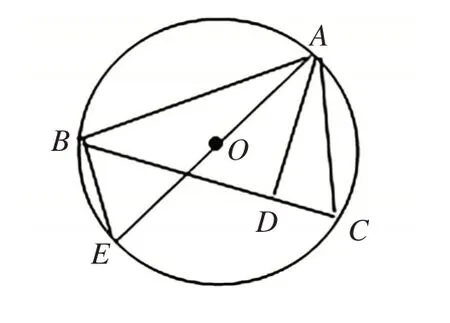
图1

在讲解此题时，可引导学生从求证的问题出发，结合相似三角形的判定定理，至少有三种方式去解决ΔADC～ΔABE：两角对应相等；两边对应成比例且夹角相等；三边对应成比例等。可以从上述三种方法选择合适的一种求证即可。

接着，可以引导学生观察所给的几何图形和已知条件，要证明上面三种情况之一成立，证明哪一种情况成立较为简便。这个题目分析到这里，大部分学生很快就能判断出证明第一种情况成立较为方便简单。因为题目所给图形和已知条件中，不难发现：∠E=∠C，∠ADC=∠ABE=90°。在充分分析下，学生选择最佳方案，教师再进行总结提升，写出规范的证明过程，完善整个思维过程。

本题的思考方法是演绎推理分析法，教师在教学时若能充分注意分析与综合，就可以启发学生去积极思考，培养他们分析问题和解决问题的能力。如果学生在学习中能运用分析法和综合法，很容易就能找到解题的途径，避免盲目摸索。因此，教师必须把分析法和综合法作为演绎推理中的有机部分，随时渗透到教学中。分析法和综合法虽然是两种相反的思维方法，但是在解题时经常把两者有机融合，避免造成思路单一的情况，这种方法就是综合分析法。本例题就体现了转化（化归）的分析综合法：由弧相等转化成圆周角相等。在整个初中数学教学中，转化（化归）方法一直贯穿其中。它是把一个未知(待解决)的问题化为已解决的或易于解决的问题来解决，如化繁为简、化难为易，化未知为已知，化高次为低次等，是解决问题的一种最基本的方法，也是数学基本思想方法之一。

二、变单一思维为多向发展，提高分析能力

学生的认知水平是逐渐上升的，在数学复习课的教学中，除了让学生对所学的知识要进行查漏补缺外，还需要“让学生再一次发展”。在教学中，要让学生把所学的知识结构化，在学科系统内有机融合、整体构建、创新方式、有效推进，这需要教师智慧地整合教学资源，把已学知识串成“线”，织成“网”。如果说新授课是数学教学的“画龙”之作，那么复习课则是“点睛”之处。以复习课“实数运算”为例，可以将整个教学设计得图文并茂、形象直观，创设各种问题情境，激发学习兴趣，进而更好地发展和提升数学思考力。

如图2，一张长方形纸片，长为2，宽为1。

问题1：长方形纸片的周长是多少？

问题2：长方形纸片的面积是多少？

问题3：将长方形纸片按图2，折出一个边长为1 的正方形，则正方形的面积是多少？

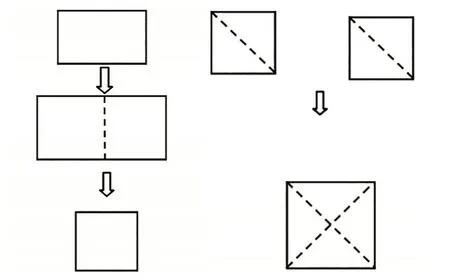
图2

问题4：如果将上述边长为1 的两个同样的正方形拼成一个的新正方形。此新正方形的边长是多少？

通过问题组的设计，可以将运算的视角引入到乘方运算，让学生感受乘方与开平方是互为逆运算。这样，既降低了对开方运算的认识难度，又让学生感受了数学中的某些规则具有一致性、相容性、和谐性。同样的，还可以得到开立方运算，立方根的概念。在问题4 中，如果学生不会求新正方形的边长，可启发他们从两个方向入手，一是通过追问：拼成的新正方形的面积可求吗？进而让学生通过新正方形的面积求出边长。二是直接利用勾股定理，得：边长=让无理数登场，以便学生更深层次地理解无理数、研究无理数。

通过以上的回忆与思考，还可以引导学生进一步探究。

如图3，如果我们沿所得边长为1 的正方形的对角线剪出一个等腰直角三角形，记为ΔABC。沿CE折叠ΔABC纸片，使A点落在BC边上的D点处。

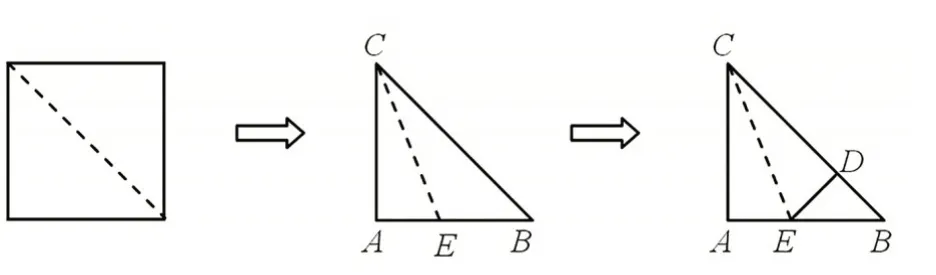
图3

问题5：求BD的长度。

问题6：如图4，继续折叠，使点B与点D重合，折痕为FQ，请你求出此时线段DQ的长度，并比较此时的DQ的值与的大小关系。

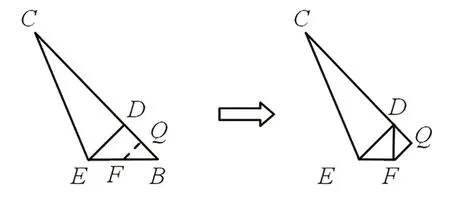
图4

问题7：对于an=b，若给出a、n，求b，是乘方运算；若给出b、n，求a，则是开方运算；若给出a、b，求n，这又是一种什么新的运算呢？

在这个设计中，由“形”出发，从互为逆运算的角度，重温数系的发展进程，让学生感受了数学六种运算的发展过程。重走发现之路，基于算理，回归估算，让学生感受到要研究这种运算的必要性和可能性，体验思维推理活动。问题7 则让不同的学生在数学上都能得到良好的发展，延续了本节课研究运算的一般方法与规律，让他们有研究运算的意识呈现，有怎样定义运算的方法倾向，有研究问题的经验积累，而这也是初高中知识衔接的重要方式之一，是教学的价值所在。

三、借助题目变式教学，拓宽逻辑思维空间

学生具有合理的逻辑习惯和较强的思维能力，不但有助于透彻地理解和系统地掌握数学知识，而且有助于提高运用数学知识解决实际问题的能力。数学教学不应该以知识的密度来代替对学生思维能力、思想方法的考查，而是应将合理推理和演绎推理巧妙地融合其中，从根本上提高学生的数学素养。对于内涵丰富的题型，若能深入挖掘，加以变化，往往能举一反三，达到以例代类的效果。即能通过做一道题达到会一类，甚至知一片的目的。

如图5，点E是△ABC的边AC延长线上的一点，点D为边AB上一点，BD=CE，连结DE，交BC于F，DF=EF，求证：AC=AB。

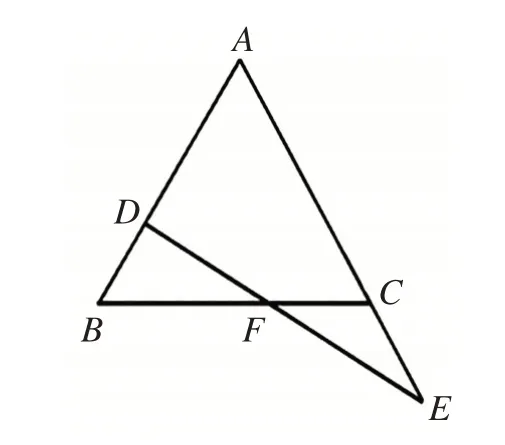
图5

解法一：在线段BF上截取GF=FC，连结DG；

解法二：过点D，作DG∥CE交BC于点G；

解法三：延长FC至P，使得FG=BF，连结EG；

解法四：过点E作EG∥BD交BC的延长线于点P。

同一个题目，从不同的角度去分析研究，可以得到不同的启发，要引导学生延伸思维的触角，激发学习兴趣，从而提高思维的广阔性、灵活性和深刻性，使其更具有思考力。还可以把题目再进行变式训练。

【变式训练1】如图5，ΔABC中，AB=AC，延长AC到E，使得CE=BD，DE交BC于F。求证：DF=EF。

启发学生多种方法去思考：利用全等三角形，利用中位线，利用平行四边形性质，进而类比相似三角形的知识。

【变式训练2】如图6，BD=CE，求证：AC·EF=AB·DF。

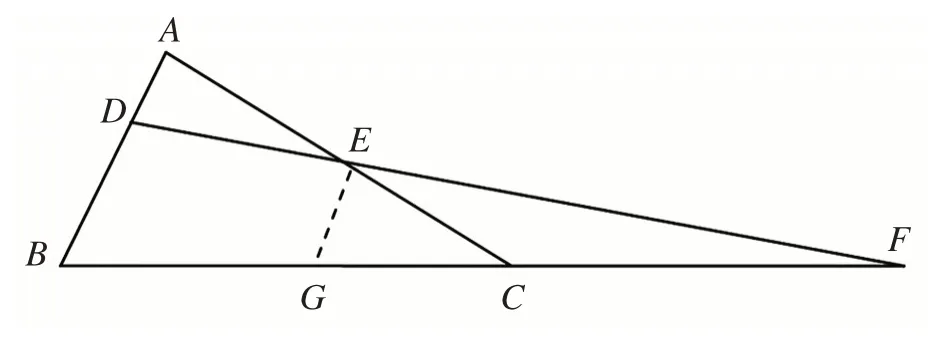
图6

有了以上两题的图形模型，结合相似三角形的有关知识，欲证等积式，只须证比例式即可。从图6中可知，AC与AB不在同一直线上，而DE与EF在同一直线上，联想到有关证明比例式的内容不外乎平行或相似得到比例式，DE与EF在同一直线上启发我们可过E点作AB的平行线。这样，就符合要求了。

“变一变，天堑变通途，换一换，陌生成熟悉。”教学中通过对例题、习题做多角度、多方面的发展，寻求问题的增长点，有意识地引导学生通过一题多解、一题多变等训练，不断摸索结解题的捷径，能够使学生思维的广阔性得到发展，思维能力得到提升。

四、抓住习题本质强化探究，走出数学思维盲区

学生错题的原因是多样的，包括：隐含条件分不清，漏条件，分类不当或不分类造成逻辑上的混乱，由于思路不清晰造成计算、推理上的漏洞，主观臆断、消极定势而“误入歧途”等。这些都体现了学生思维的单一化、表面化、无序化盲区。要走出这些思维的盲区，应对他们的学习活动进行观察，选择“典型”例题进行剖析，精心引导，强化训练，并要运用变通性的动态思考。

如有这样一个题目：

在本题的解答中，很多学生往往是没有对两个方程组的构造进行比较研究，而是按部就班地将x、y的值代入第一个方程组，求出m、n，再把它们代入第二个方程组。这个方法也是正确的，但是整个计算过程比较繁冗，还容易产生计算错误。作为填空题题型，这样的题目对于学生来说失分率颇高。我们知道，对于同一类方程（组），方程的解取决于它所含的系数，而与它采用的字母无关。此题中两个方程组虽然表面不一，但只要把第二个方程组的（2x+y）、（2x-y）分别看成两个整体换元，那么它与第一个方程组的系数就相同，因而它的解也应该相同，即有这样就抓住了习题的本质，运用了解方程的思想进行了处理。在平时教学中，应使知识的发生过程与结论浑然一体，以强化探究的教学方式去克服学生数学思维的盲区，使学生的思考力得到更进一步的发展。

美国数学家波利亚认为，中学数学教育的根本目的是“教会学生思考”。我们应当明确，数学教育的目的不是培养知识的记忆者，而是培养积极的思考者。教师的角色起着关键性的作用，特别是要准确把握习题的关键点，精心设计习题，组织学生操作实验、观察现象、提出猜想、推理论证等，引导其灵活、多角度地思考，有效提升思考力。