小学数学结构化教学的三个维度

张 静

（江苏省盐城市串场河小学）

数学中的每一个知识点都隶属于某一个知识体系，而不是孤立存在的，有时需要考虑学生的认知规律及教材的编排。教材切断了知识链条，使知识点在其中犹如“散落的珍珠”分散在不同的学段里，有时还穿插着其他的数学知识。因此，教师需要像海边的“捡贝”一样，要将学生分散的、断裂的“碎片化”知识这种“珍珠”串成“项链”，将知识结构化，让学生看清知识完整的样子，明白知识的形成过程，联结学生的认知结构和思维体系，构建整体的结构化思维。

一、以研读教材促知识结构化，为深度学习提供保障

数学教材是进行数学教学的媒介，也是数学知识的载体，但它仅为课堂教学提供了最基本的材料。因此，需要教师认真地研读教材，去调整、去丰富、去完善，使数学教学过程更能站在学生的立场，贴近学生的思维，使其更富有挑战性。

（一）以通读了解教材整体架构

德国数学家克莱因认为，数学教师的职责是“应使学生了解数学并不是孤立的各门学问，而是一个有机的整体。”对于教师来说，要认真研读《义务教育数学课程标准（2011年版）》，将小学数学知识和内容真实、准确地理解并在教学中实施，帮助学生形成自己的知识体系，建构自己的知识结构。了解教材的整体知识架构，可分两条线，一条是按学段、分年级进行，另一条按照知识发展的先后顺序。

如北师版《义务教育教科书·数学》六年级上册教材，教师首先要通读课程标准中关于六年级数学上册的教学目标及具体要求，了解新学期安排了哪些学习内容，需要掌握哪些新的知识，了解各单元教材的课时安排及怎样突破各单元重难点，教师只有整体把握教材结构，才能有效地实施教学活动。可以将教材整体知识结构进行整理。（如图1）

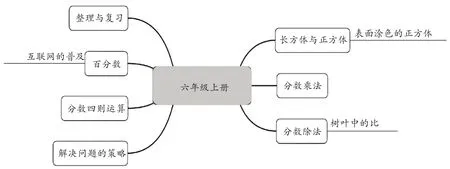
图1 六年级上册整体知识结构

整体把握教材还可以按照知识结构体系，小学数学教材分四个领域去编排，分别是数与代数、图形与几何、统计与概率、实践与综合运用。如图形与几何这个知识领域，可以用结构图，帮助我们直观解读图形与几何领域的知识架构。图形与几何领域分两类，平面图形和立体图形，平面图形由点、线、角、面（多边形与圆）组成，然后再按照边和角的特征把多边形进一步分类，随着分类，它们之间的联系和区别逐渐呈现出来。而如图2 的结构图，能直观地把平面图形知识之间的关系联结起来。同样，立体图形分两块：一块是长方体、正方体、圆柱和圆锥的基本特征，另一块是这几个立体图形的表面积和体积计算公式及推导之间的逻辑关系，以及运用这些公式解决生产生活中的实际问题。

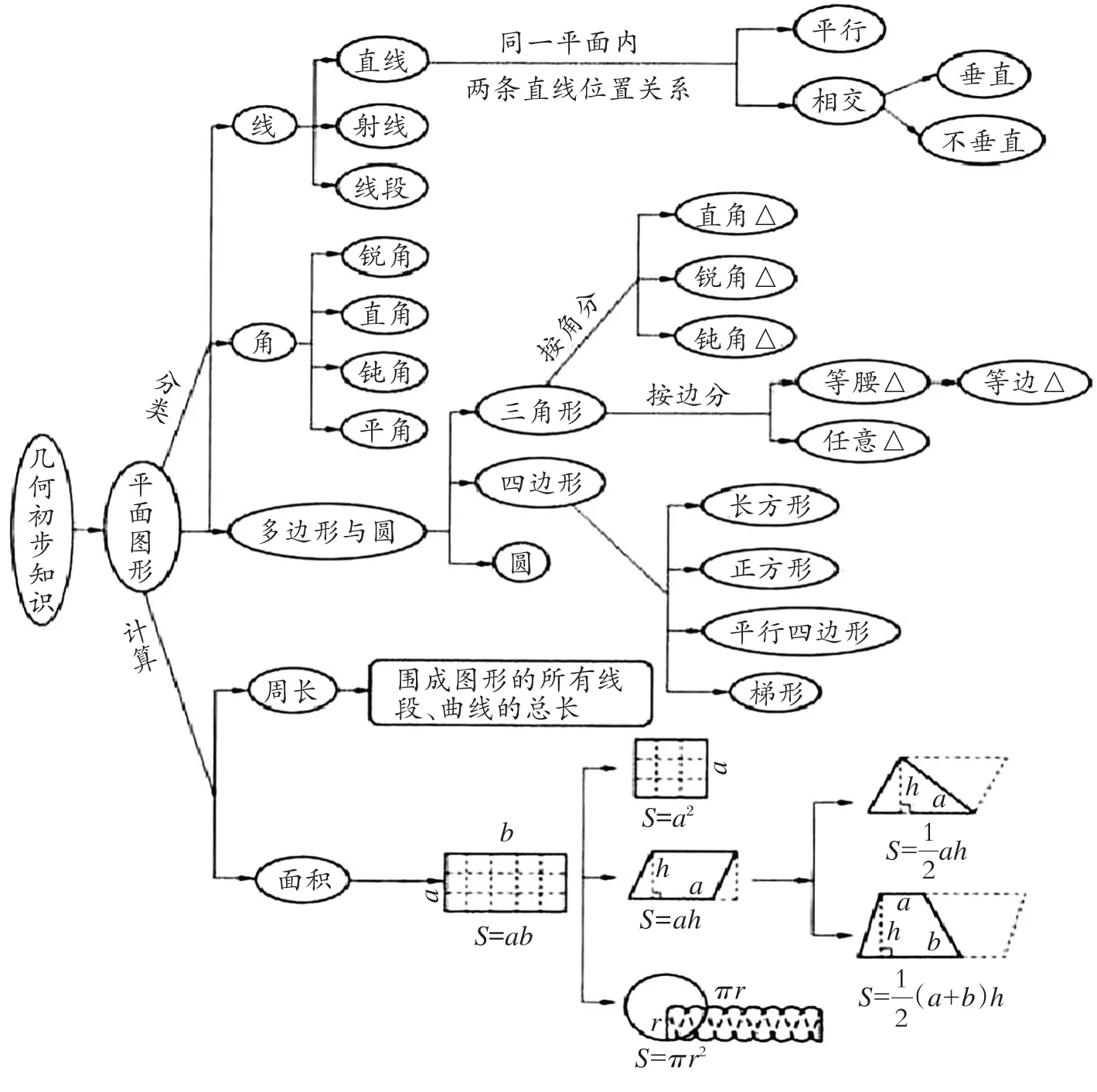
图2 平面图形知识结构

（二）以联读把握单元教材结构

在教学具体单元内容时，首先要了解这个单元教材设置了哪些内容，课时怎样划分，知识前后有什么联系，配套例题与练习是怎样安排的。其次，要多提几个问题，促使自己进一步去解读教材。最后，教师一定要了解学生在学习本单元知识前，他们已经具备了哪些生活经验和学习经验，本单元知识的安排有怎样的层次，知识之间有怎样的联系，将本单元知识进行梳理，形成清晰的单元教材结构。

如以五年级“式与方程”单元为例，根据课程标准和对教材的解读，本单元的知识结构导图可设计如图3。

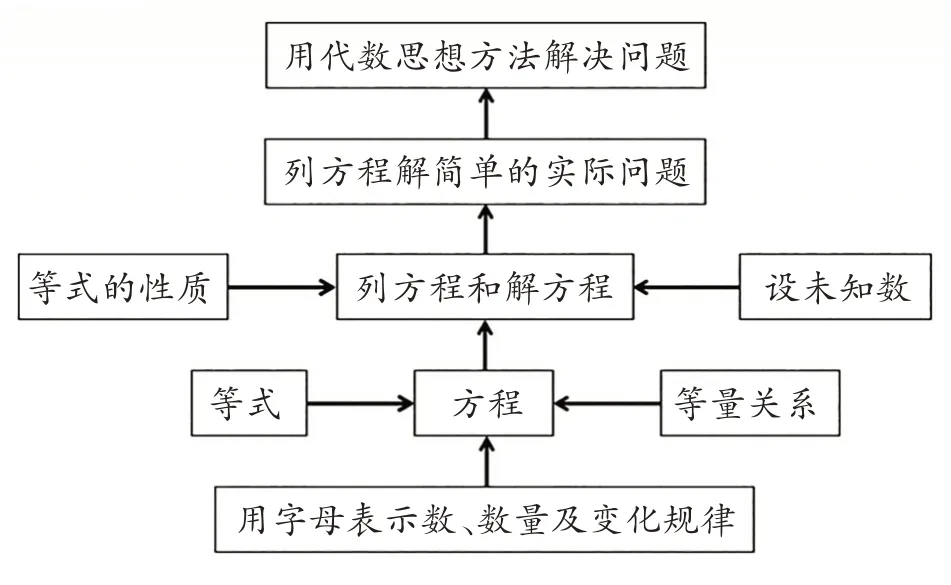
图3 “式与方程”知识结构

有了对单元教材结构的解读，可以采取相应的教学策略：首先，让学生在一定的现实情景中体味用字母表示数及数量关系的好处，理解方程的意义，学会分析现实情境中的数量关系，能根据等量关系列方程，熟练运用等式的性质解方程，在解决具体问题的过程中，相机渗透方程思想，培养代数意识。其次，创设丰富的教学情境，解决教学中的难点，让学生掌握找等量关系的方法，明确同一问题，由于等量关系的不同，所列方程不一样，进一步沟通不同解法之间的区别及联系，帮助学生掌握列方程解决实际问题的思考方法，提升学生解决问题的能力。最后，通过列方程解决实际问题，体会顺向思维的优势，培养学生代数思维，有助于初小衔接，为学生的可持续发展奠定坚实的基础。

（三）以比读理解课时教材结构

在了解了教材的整体知识结构和把握一个单元的内容结构之后，教师还要考虑课时备课，除了要了解本课时的教学内容以及前后知识之间的联系，还需要通过对不同版本教材的比读，便于我们更清晰地认识教材，更精准地实施课堂教学。

如“三角形的认识”，苏教版修订版教材通过学生画三角形，加深了学生对三角形本质属性的理解，其沿袭了实验版教材的一些好的做法，从生活情境中抽象出三角形，将三角形的高与生活中的高密切联系起来，有助于学生对数学中“高”的意义理解。而人教版教材给出用字母表示三角形三个顶点的方式，便于学生表述具体三角形，其对锐角、钝角、直角三角形的高进行了比较，帮助他们形成了比较清晰的认知结构。浙教版教材则是将内容整合，按图形的边、图形的角、图形的高与底分课时进行学习。因此，我们在教学时，可以借鉴人教版教材内容，增加用字母表示三角形的环节，也可以借鉴浙教版教材内容，介绍钝角三角形短边上的高。

二、以研究课堂促认知结构化，为深度学习提供实践支撑

结构化学习，是指努力去寻找知识点之间的连接，将零散的、碎片化的知识连成线、织成网，形成块，让学生不仅看清知识的来时路，还能看清知识的整体架构。同时，帮助他们依据自己的理解、用自己的语言重新梳理一个新的知识框架，形成一套属于他自己所熟悉的、全面的知识体系，建构起的认知结构。如六年级“平面图形的面积”一课，可分三个层次进行教学，以促进学生的认知结构化。

（一）通过整理，看清知识的来龙去脉

课前，应组织学生再次阅读教材，完成学习单，引导他们形成复习的一般思路。课中，可以让学生说一说、议一议平面图形的面积公式及这些公式的推导过程，寻找公式推导之间的联系，再试着将它们进行梳理。学生在独立整理中会对这些面积公式及推导过程进行再次复习，并自主整理，看清知识的本质。在教学中，不仅让学生学会自主整理的同时，还应介绍、推荐整理的新方法——思维导图法。

（二）通过建构，完善系统知识链

建构主义理论强调，学习不是简单地让学生占有别人的知识，而是主动地建构自己的知识经验，形成自己的独特见解。为此，在本中我课进行了两次建构：第一次建构，以长方形的面积为中心，建构平面图形面积推导之间的联系，学生经过独立思考、组内学习、集体交流，理清了知识之间纵向、横向的内在关联，了解各个平面图形面积推导公式之间的相互联系，构建了清晰的知识网络结构。在获得数学知识的同时，也学会了归纳整理的方法，构建完善的系统链。（如图4）第二次建构，以梯形的面积计算为中心的结构图，成聚拢状结构。在梯形面积变化过程中，让学生体会到平面图形面积公式是有联系的，平面图形的面积计算方法都是相通的、可以相互转化的，可以统一用梯形的面积公式去计算。（如图5）

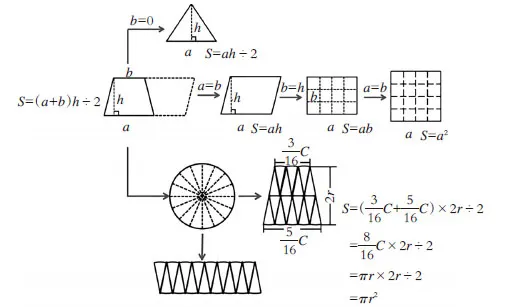
图4 平面图形面积推导联系

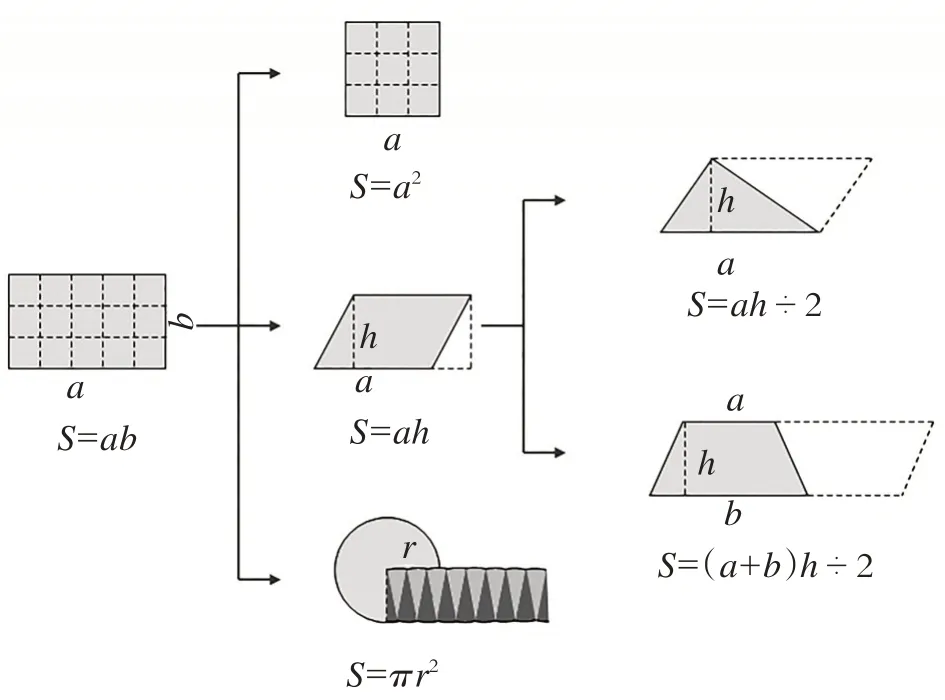
图5 平面图形面积计算联系

（三）通过应用，构建完整的认知结构

在练习环节，我设计了“画出面积是18 平方厘米的三角形、平行四边形和梯形”的练习，并追问：当它们的高（底）和面积相等，底（高）之间有怎样的关系？这不仅是对本课所学计算方法联系的再次应用，更提升了学生的画图能力。最后，我设计了一个数学故事作为结尾，不仅渗透了周长相等，圆的面积最大，还阐释了数学与人生的哲理，对学生的情感态度价值观再一次洗礼，提升了学生的数学素养。

结构化，不仅要帮助学生沟通知识间的一般联系，更要让他们在此基础上构建完善的认知结构；不仅要让学生通过梳理知识，完善认知结构，还要帮助他们形成方法结构、思维结构，帮助其对所学知识进行整体架构，形成完整的知识链，实现知识的同化或强化。

三、以研究学生促思维结构化，让深度学习真正发生

结构化教学，不仅要研究教材、研究课堂，更要研究学生。当学生在面对数学问题时，能从已有的众多的经验中，抽取出与当前问题相关的经验，迅速作出判断、解决问题的合适方法，并能有效解决，这种让他们经历发现与分析问题、探索与解决问题的过程，就是将知识结构化逐渐内化为学生的认知结构化，进而形成结构化思维。

（一）让知识成“串”

有些数学知识表面看起来毫无关联，但实际上它们之间却是纵横联系的。如在教学“圆柱的表面积”时，我首先让学生回忆圆的面积公式是怎么推导的，把圆沿直径切成n等分，拼成近似的长方形，根据长方形的面积推出圆的面积公式。接着，再让学生画出圆柱体表面积展开图，即把侧面沿高剪开得到一个大长方形，把两个底圆沿直径平均分成若干等份，分别拼成两个近似的小长方形，已知小长方形的长是底圆周长的一半（πr），此时有学生将两个近似小长方形放在大长方形的正上方，正好构成一个新的长方形，这个新长方形的长就是2πr，高就是h+r。这样新长方形的面积即为S=2πr（h+r），也就是圆柱体的表面积（如图6）。这样，圆的面积看上去好像跟圆柱的表面积无关，学生却利用几何图形形象生动地诠释了圆柱体表面积公式S=2πr（h+r）。由于抓住学生善于利用形象思维来认知事物，充分让他们经历了“数”与“形”的诠释过程，巧妙地把以前学过的圆面积的知识和圆柱表面积串连起来，这样纵向勾连，有助于形成结构化的思维方式。

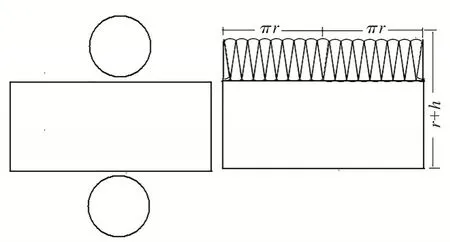
图6 圆柱体表面积展开

（二）让策略成“续”

教材非常注重解题策略的教学，从基本策略（从条件想起，从问题想起）到特殊策略（列举、画图、转化、假设等），其在策略单元教学安排中，都有一个很好的教学环节，就是回忆以前的数学教学中哪些地方用到相关的策略。作为教师，不仅要透彻了解本课时的教材内容，还要从策略链的视角全面研读教材，握教材的持续性，掌握新知识的生长点。如在教学“转化”这节课时，我先让学生回忆以前在哪里运用过转化的策略，有的学生说是在学习异分母分数加减法时，转化成同分母分数加减法；有的学生说学习小数乘除法时，转化成整数乘除法计算；还有的学生说平面图形的面积公式推导也是用转化。此时，需要让学生思考：为什么要转化？用什么知识转化？为什么能转化？这些知识表面看似毫无关联，但因为它们所用的策略相同，续接成串，形成了清晰的知识链。

（三）让结构成“系”

学生的经验不仅包括知识经验，还包括方法经验、思维经验等，结构化教学关注方法结构的形成，让学生在旧知学习中形成的方法迁移到新知中，使方法在循序连环的使用中扎根生长。教材中有很多探究规律的知识，如小数的性质、商的变化规律、间隔排列、运算律等。在教学中，要引导学生经历探究发现规律的一般性过程：猜想、验证（列举）、结论、解释、应用等环节，让他们模拟经历一个科学家发现的过程，激发其的探究热情，体验成功的愉悦，建立解决问题的方法结构及思维结构，形成整体、系统的意识。这样，在遇到新问题时他们才能自觉地去寻找方法，将新问题纳入旧的知识结构中，实现知识的同化和顺应。

总之，实施结构化教学有助于教师用整体、连续的视角理解教材，合理地把握知识的整体架构。在教学中，教师要用结构化思维研读教材，设计教学流程，根据学生的年龄特点和认知规律，合理有效地开展教学活动，帮助学生理解和掌握数学的知识结构及方法结构，形成较完善的认知结构和数学思维结构，促进深度学习。