基于多变量最小二乘法和粒子群优化的金团簇结构预测

孙悦 刘佳奇 侯冬雪 高闯

摘  要：团簇科学是凝聚态物理领域中非常重要的研究方向，该文以金属团簇金Au20为研究对象，利用999组已知的结构数据，运用最小二乘法通过最小化误差的平方和寻找数据的最佳函数匹配简便地求得未知的模型参数，进而建立金团簇Au20的Gupta能量预测模型。结合金团簇的能量预测模型，利用粒子群优化算法进行对原子结构进行优化，最终运用VMD软件进行金团簇的全局最优结构重构，验证模型的有效性和可行性。

关键词：原子团簇   结构优化   Gupta势能函数   粒子群算法

中图分类号：TB383.1                      文献标识码：A文章编号：1672-3791（2021）06（c）-0188-04

Structure Prediction of Gold Clusters Based on Multivariable Least Square Method and Particle Swarm Optimization

SUN Yue   LIU Jiaqi   HOU Dongxue  GAO Chuang*

（School of Electronic and Information Engineering， University of Science and Technology Liaoning， Anshan， Liaoning Province， 114051  China）

Abstract： Cluster science is a very important research direction in the field of condensed matter physics. This paper takes Metal Cluster Gold Au20 as the research object， uses 999 groups of known structural data， uses the least square method to find the best function matching of the data by minimizing the sum of squares of errors， easily obtains the unknown model parameters， and then establishes the Gupta energy prediction model of gold cluster Au20. Combined with the energy prediction model of gold clusters， particle swarm optimization algorithm is used to optimize the atomic structure. Finally， VMD software is used to reconstruct the global optimal structure of gold clusters to verify the effectiveness and feasibility of the model.

Key Words： Atomic clusters; Structure optimization; Gupta potential energy function; Particle swarm optimization

团簇研究正在迅猛发展，是跨越原子、分子物理、固体物理、表面物理、量子化学等诸多学科的一个交叉学科。但由于团簇的势能曲面上存在着大量的局部极值，同时需要考虑相对论效应等，所以要想找到团簇的全局最优结构是十分困难的。传统的计算方法中随着原子数的增加，高精度的理论计算时间呈现指数型增长，耗时严重。所以，团簇能量预测模型的研究在很多方面还需要不断完善。基于惯性权值非线性递减的改进粒子群算法或结合自适應免疫优化算法和动态格点搜索操作以及无偏优化算法优化了团簇的最稳定结构，具有较高的计算速度和成功率，但需要指出的是团簇的初始构型是随机生成的，内部操作也有一定的随机性，因此应对该方法进行进一步的改进[1-3]。基于CALYPSO结构预测方法和密度泛函理论的第一性原理、粒子群优化算法，结合随机学习、竞争机制以及变异算子、多种经典启发式算法、动态格点搜索算法以及遗传算法结合密度泛函TPSS对势能面提出了一些高效的、无偏的优化算法[4-8]。与上述文献的建模方法不同，该文采用多变量最小二乘法和粒子群优化算法，通过智能方法建立金团簇的能量预测模型，并利用该模型找到金团簇的最优原子结构，最后通过VMD软件对原子结构进行重构，进行稳定性分析，验证所提出模型有效性。

1  模型的建立与求解

1.1 数据预处理

选取999组金团簇Au20的结构异构体数据，利用MATLAB软件进行数据预处理，具体步骤如下。

Step 1：将每组的三列数据放至一列，设置两个变量n1，n2，分别从0～99，100～154，156～199，200～299，300～399，400～499，500～599，600～699，700～799，800～899，900～999对其赋值，共11组。

Step 2：利用for循环和num2str函数先将i变量转换为字符型。

Step 3：用textread函数对数据进行读取得到A1 cell文件，后用str2num函数将其转换为double型进而得到向量m。

Step 4：设置一个空矩阵B，将m中的一列数据分为每列61行存放在矩阵A中，将A赋值给B，得到最终处理好的数据。

Step 5：重复Step2～4，完成全部11组数据的预处理，得到999列的建模数据B。

1.2 基于多变量最小二乘法的Gupta能量预测模型

为了建立金团簇的Gupta能量预测模型，基于999组实际数据，可采用多变量最小二乘法回归出金团簇的势能预测模型。Gupta势函数可描述金团簇中金原子之间的相互作用。Gupta势函数可以分解为斥力项Vr（i）和引力项Vm（i），对于原子总数为N的团簇势能函数Vn表述为[1]：

（1）

（2）

其中，N为团簇原子总数;rij代表原子i和j之间的距离;rij是最近邻近平衡距离;Aij是斥力项系数;ξij代表原子i和j之间的有效跳跃积分参数;pij和qij分别描述为对斥力与引力作用的权重。

上述模型中的除了N和rij的其他5个参数可采用多变量最小二乘法，结合999组数据，对参数进行辨识，最小二乘法是一种常用的数学优化方法，它通过最小化误差的平方和寻找数据的最佳函数匹配。它可以用于函数曲线拟合。在无约束最优问题中，其目标函数可表示为：

（3）

其中，Li（x）是x的非线性函数，该题的Li（x）选择为Gupta势函数。具体建模步骤如下。

Step 1：读取999组实际数据，设定5个待辨识参数的初值。

Step 2：根据数据中的坐标信息，计算出各个原子之间的距离rij。

Step 3：在MATLAB中调用最小二乘lsqcurvefit函数，将初值和距离rij代入函数中进行计算。

Step 4：通过lsqcurvefit函数的返回值Cof，得到辨识后的5个参数实际值。完成金团簇的Gupta能量预测模型建模。

1.3 基于粒子群算法的金团簇结构优化模型

建立Gupta能量预测模型后，可利用粒子群优化算法对各原子之间的距离进行优化，得到势能更低的金团簇结构异构体。该算法具有独特的搜索机制，是受鸟群捕食行为的启发而提出来的一种群体智能优化算法，其数学描述为：設在一个D维搜索空间中，每个粒子是一个点，粒子规模为N，第i个粒子的位置矢量可以描述为xi=（xi1，xi2，…，xid），速度矢量可描述为vi=（vi1，vi2，…，vid），第i个粒子搜索到的最优位置为pi=（pi1，pi2，…，pid），称为个体极值，表示粒子的个体经验;整个种群搜索到的最优位置为pg=（pg1，pg2，…，pgd），称为全局极值，表示粒子的群体经验[4]。粒子的速度和位置更新公式如下：

（4）

式中，w为惯性权重;k为当前迭代次数;C1和C2为加速因子，是非负的常数;r1和r2是分布在[0，1]之间的随机数。

利用上述公式，可完成金团簇原子距离的优化，具体建模步骤如下。

Step 1：初始化种群数量、迭代次数以及原子数量等粒子群参数。

Step 2：随机生成初始种群（原子坐标）的初始解，将初始解代入Gupta势函数（1）和（2）中，计算出各个势能值。

Step 3：根据当前的最优解，利用式（4）的更新规则求出种群下次迭代的位置。

Step 4：重复Step 2和3，达到最大迭代次数时，得到最优解，即为本次运行的全局最优解，其对应的20个原子坐标组成的金团簇是全局最优结构。

2  结果检验

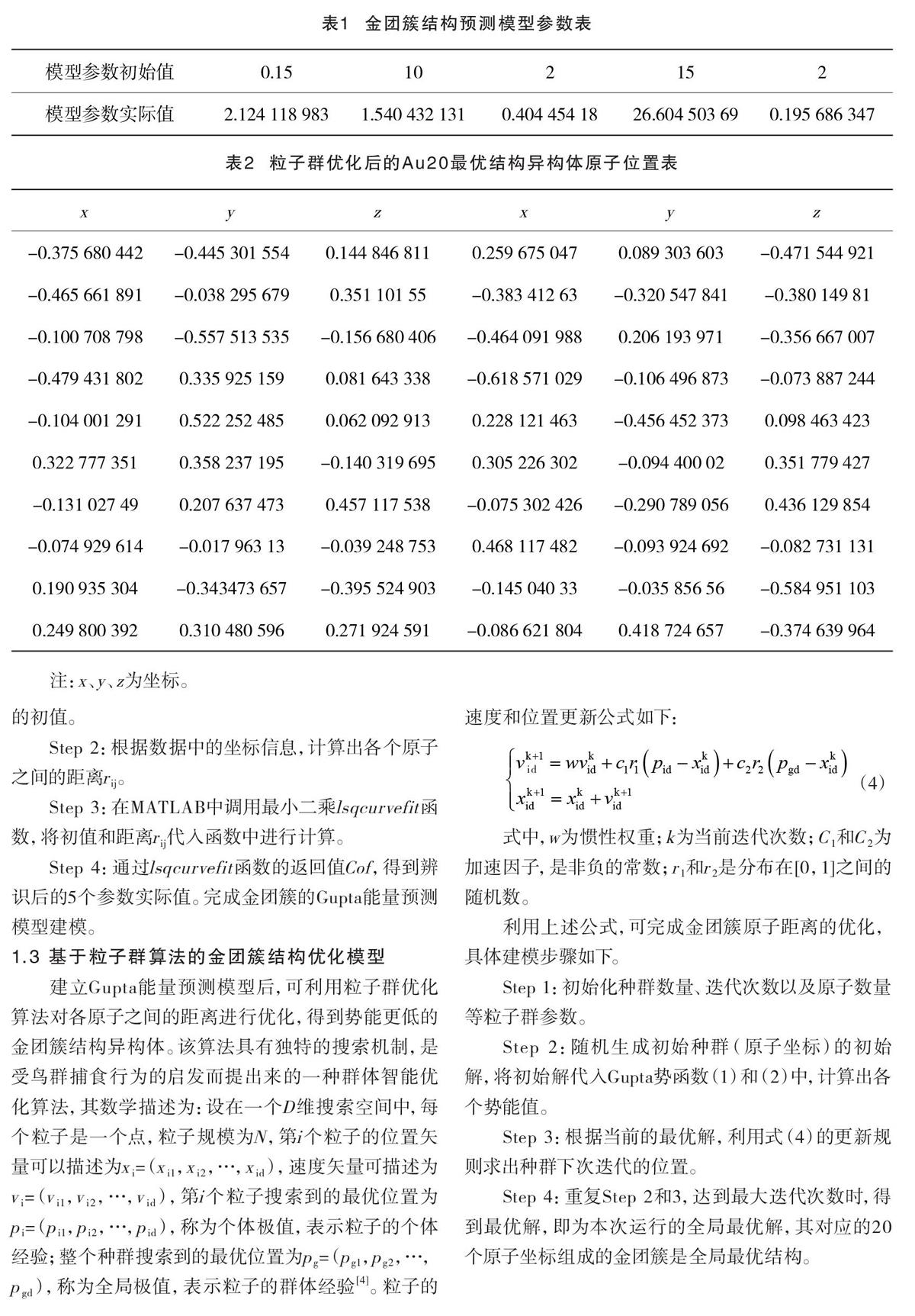
根据1.3的建模步骤，利用MATLAB软件进行仿真，可建立金团簇结构预测模型。模型的初始值和实际值见表1。

根据1.3的建模步骤，设置PSO的种群数量为50，迭代次数为2 000，可找到金团簇Au20的全局最优结构，最优结构的原子坐标信息见表2。

Au20的全局最优结构见图1，从图中可以看出，四面体结构的Au20纳米团簇具有配体保护的金纳米团簇中的荧光将团簇聚集源与定制的离子光学和大量选择过程相结合，创造出了一束裸Au20簇，然后把它们植入固体氖基质中。它们是通过沉积具有氖背景气的团粒束获得的，然而氖气是一种惰性气体，与其他物质相互作用较弱。氖中固有的结构和光学团簇性质在实验中能够得以保留，因此稳定。

3  结语

该文利用多变量最小二乘法，可以更简便地获取模型所需参数，提高了模型的预测效率;Gupta模型的适用范围很广，能够允许除该文所用的数据进行能量预测，进而找到可能存在的最优化结构，体现了模型的实用性和合理性。后续工作，可采用更高效的元启发式优化算法替代，可获得更准确的模型参数;粒子群算法的程序里较大，算法复杂，可采用更简便的优化算法替换，例如鲸鱼群优化算法等，优化策略更简单高效。

参考文献

[1] 吴夏，董彦杰.Gupta与Sutton-Chen势函数的金团簇稳定结构[J].计算机与应用化学，2014，31（11）：

1333-1336.

[2] 周营成.基于群智能和机器学习的新型纳米团簇结构预测研究[D].北京：北京化工大学，2020.

[3] 宋婉婷，孙彤，张如杰，等.Au_mY_n（m+n≤6）团簇的结构、稳定性及电子特性研究[J].分子科学学报，2019，35（6）：503-508.

[4] 华勇，王双园，白国振，等.基于惯性权值非线性递减的改进粒子群算法[J].重庆工商大学学报：自然科学版，2021，38（2）：1-9.

[5] 周营成.基于群智能和机器学习的新型纳米团簇结构预测研究[D].北京：北京化工大学，2020.

[6] 熊荆武.预测Au团簇基态结构的启发式优化算法[D].武汉：华中科技大学，2017.

[7] 汪光炼.预测Au团簇基态结构的动态格点搜索算法[D].武汉：华中科技大学，2015.

[8] 田志美.配体保护金团簇的结构预测及电子结构分析[D].合肥：安徽大学，2018.