最大化子阵列增益的多用户大规模MIMO混合预编码*
2021-09-29高俊枫
张 雷,高俊枫,向 博
(成都大学 电子信息与电气工程学院,成都610106)
0 引 言
大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)是第五代移动通信系统(5G)及未来移动通信的关键技术之一,它通过在基站配置数十至数百个天线,并结合发射预编码和接收合并处理,能极大提升系统频谱效率和功率效率[1-3]。在下行传输中,大规模MIMO理论上需采用全数字预编码以获取最优性能。然而,基带的数字化处理要求天线阵列每个阵元具有独立的射频链路。相较于传统MIMO,大规模MIMO阵元数量巨大,导致复杂度、成本和功耗急剧上升,从而制约了其实际应用。由此,学术界提出了射频链路数远小于基站天线数的“基带低维数字预编码+射频高维模拟预编码”的模数混合预编码方案[4]。
模拟预编码通常用移相器实现,而早期大部分混合预编码针对全连接结构设计[4-6],即每个射频链路通过移相器与所有天线相连,所需移相器数等于天线数与射频链路数之积,成本和功耗仍然较高。因此,又提出了基于部分连接结构的模数混合预编码[7-10],即射频链路仅与互不交叠的天线子阵列相连,故所需移相器总数等于天线数。其中,文献[7]和[8]分别研究了单用户混合预编码中单载波情形的串行干扰消除预编码算法和多载波情形的并行预编码处理框架,文献[9]设计了注水结合迭代算法的单用户最佳混合预编码器,文献[10]则提出了同时适用于单用户全连接和部分连接结构的通用混合预编码算法。上述研究表明,部分连接结构能获得比全连接结构更好的成本、复杂度和性能折中。然而,它们也存在两点不足:一是都针对单用户系统研究,所用奇异值分解等方法难以推广至多用户情形,不能实现多用户复用增益;二是多采用迭代或搜索类等高复杂度算法,难以用于实际系统。针对采用部分连接结构的多用户大规模MIMO系统,文献[11-12]提出了“基于空口信道相位信息的块对角模拟预编码+基于等效信道矩阵的迫零数字预编码”的混合预编码方法,能获得简单闭合解和较好性能;文献[13]也将其中的模拟预编码方法用于单用户混合预编码设计。但是,这种模拟预编码方法固化了用户和天线子阵列之间的匹配关系,其性能还有较大提升空间。
本文针对文献[11-12]的不足,面向部分连接结构的多用户大规模MIMO混合预编码系统,提出一种新的低复杂度高性能模拟预编码方法。利用不同天线子阵列到不同用户的信道增益存在差异这一特点,基于最大化用户子阵列增益原则将用户和子阵列匹配,再提取每个用户对应子阵列的空口信道相位信息生成该用户的模拟预编码向量。由此构建的模拟预编码矩阵具有比文献[11-13]中块对角模拟预编码矩阵更通用的块稀疏结构,且每个用户能获得更大子阵列增益,并进而提升总体预编码增益。仿真表明,基于所提匹配准则的混合预编码相较于基于传统固定匹配的混合预编码能获得更高的系统和频谱效率。
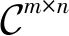
1 系统模型
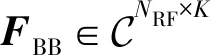
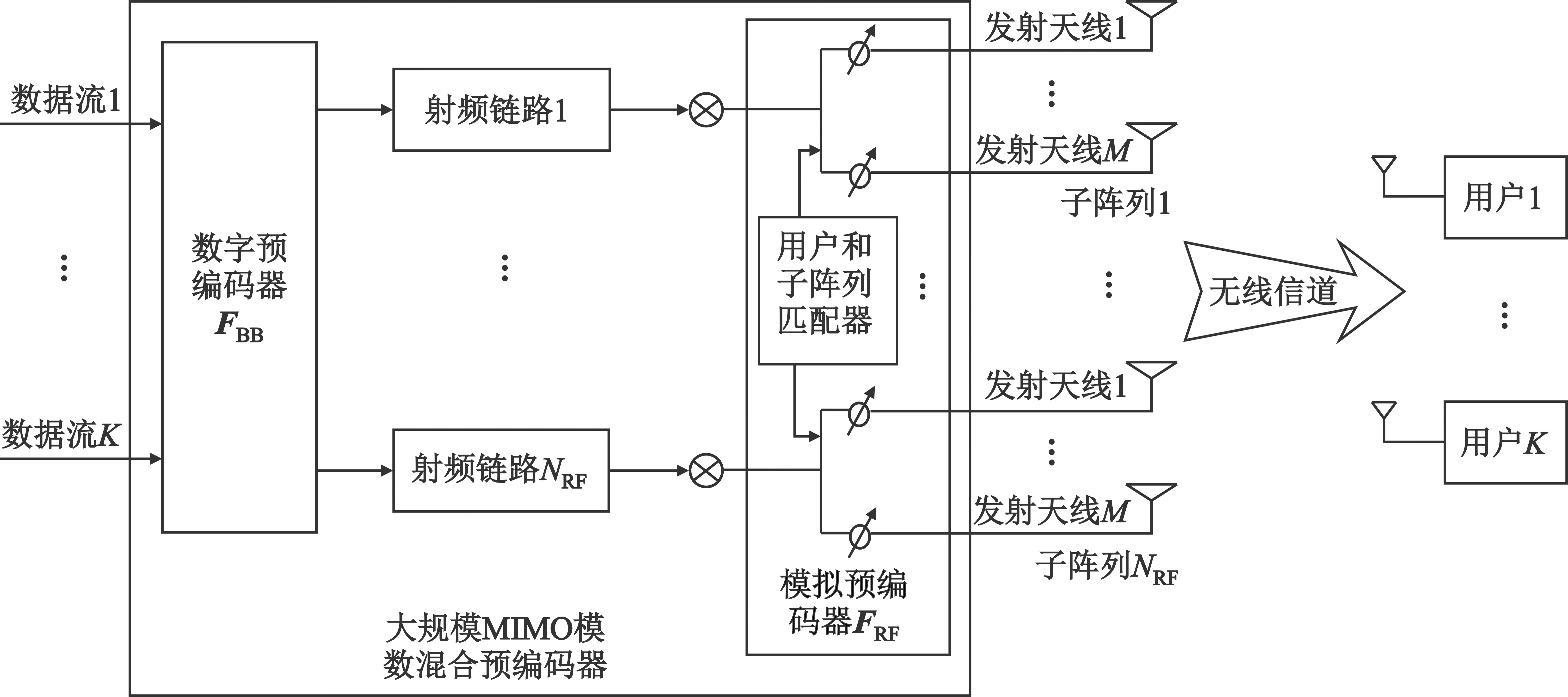
图1 部分连接结构的大规模MIMO模数混合预编码系统模型
考虑窄带平坦衰落信道。所有用户的接收信号用向量表示为
r=HFRFFBBs+n。
(1)
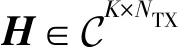
(2)
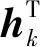
(3)
2 最大化子阵列增益的的多用户混合预编码
2.1 总体思路
设基站能通过上下行链路互易性或用户端反馈获得下行信道矩阵H。考虑到多用户的分布式接收特点,为得到混合预编码矩阵的简单闭合解,本文仍采用与文献[11-12]类似的“基于空口信道相位信息的模拟预编码+基于等效信道矩阵的迫零数字预编码”基本框架。因迫零数字预编码技术较为成熟且得到广泛应用[5-6],且已有研究表明模拟预编码获得较大子阵列增益可改善混合预编码的和频谱效率性能[12],故本文主要优化模拟预编码。从子阵列模拟预编码向量设计入手,分析发现不同子阵列到不同用户的子阵列增益存在差异,遂提出能最大化用户子阵列增益的用户和子阵列匹配准则,从而最终提升系统的和频谱效率。
2.2 子阵列的模拟预编码向量
用移相器实现模拟预编码时,通过提取H的共轭转置的相位信息实施相位控制,由此可获得类似传统等增益发送的子阵列增益[11-13]。部分连接结构中整体的模拟预编码矩阵由每个子阵列对应的模拟预编码向量组成,由此,将H按天线维度划分为NRF个子矩阵,即
(4)
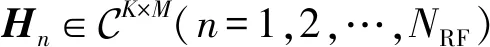
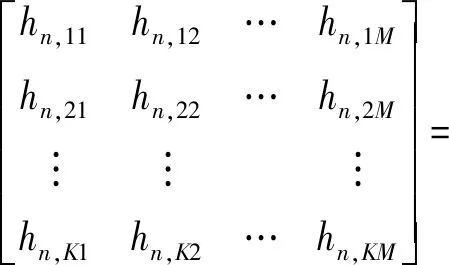
(5)
式中:hn,km(k=1,2,…,K;m=1,2,…,M)表示基站第(n-1)M+m个天线到第k个用户的信道系数,|hn,km|和φn,km分别表示hn,km的幅度和相位。
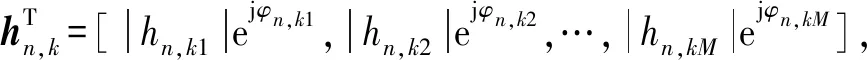
(6)
由此,可认为通过该准则在用户k和子阵列n之间建立了一个匹配关系。
2.3 用户和子阵列的传统匹配准则
在文献[11-12]的方案中,子阵列n和用户k之间的匹配关系是固定的:子阵列1、K+1、2K+1…和用户1匹配,子阵列2、K+2、2K+2…和用户2匹配,…,子阵列K、2K、3K…和用户K匹配。由此,fn可表示为(上标“C”表示传统匹配准则)
(7)
对应的模拟预编码矩阵具有如下块对角结构:
(8)
2.4 最大化用户子阵列增益匹配准则
在信道向量hn,k和模拟预编码向量fn共同作用下,用户k可获得子阵列增益ηk(n)为
(9)
注意到当M和k确定时,不同n值对应的|hn,km|值不同,因此ηk(n)是关于n的函数。因此,本文提出两种新的匹配准则,以最大化用户k的子阵列增益ηk(n)。
匹配准则1:用户顺序固定时最大化子阵列增益
设用户序号集合为U={1,2,…,K},子阵列序号集合为A={1,2,…,NRF},具体如下。
第1轮匹配。首先,对用户1,根据式(9)计算其对应的所有子阵列增益{η1(n)|n∈A},再从中选择使η1(n)具有最大值的子阵列n1∈A匹配给用户1。其次,对用户2,计算其对应除子阵列n1以外的其余所有子阵列增益{η2(n)|n∈A{n1}},再从中选择使η2(n)具有最大值的子阵列n2∈A匹配给用户2……以此类推,直至为用户K匹配了子阵列nK。
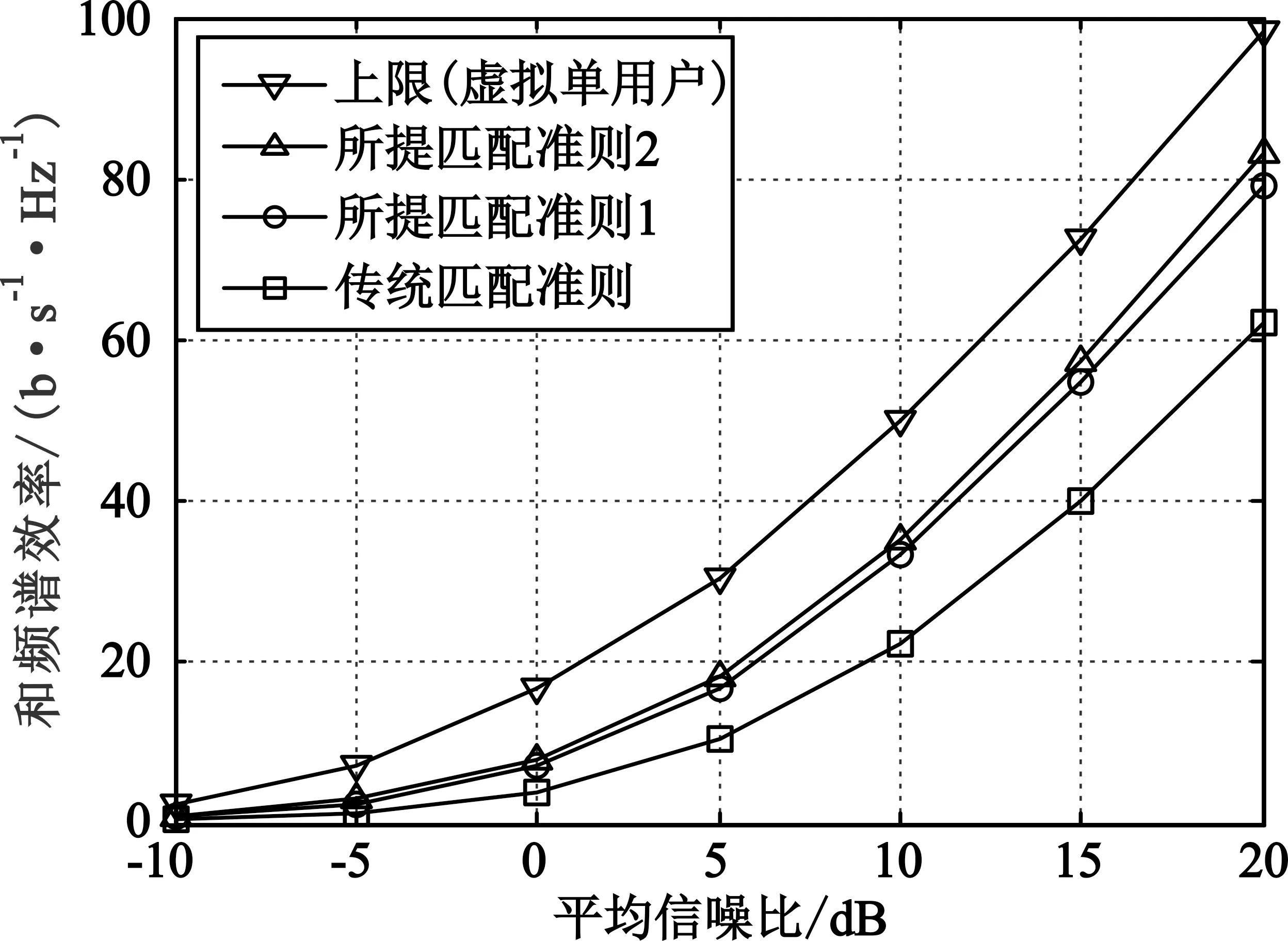
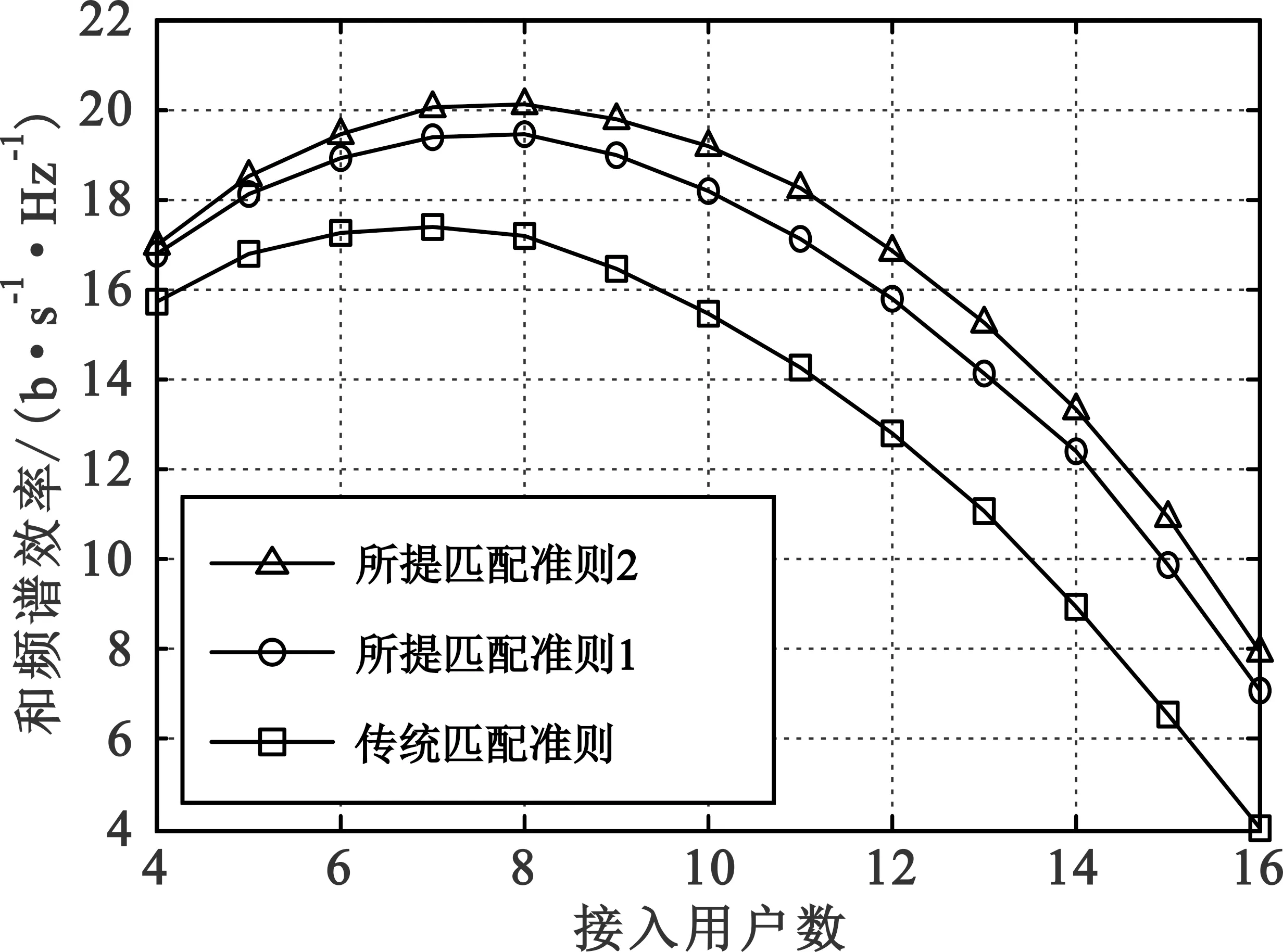
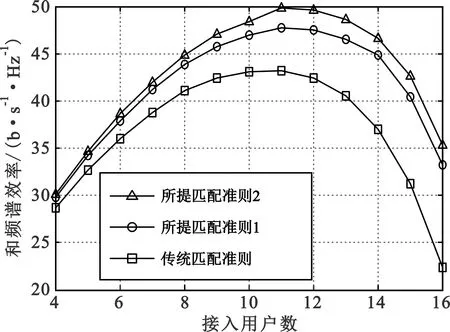
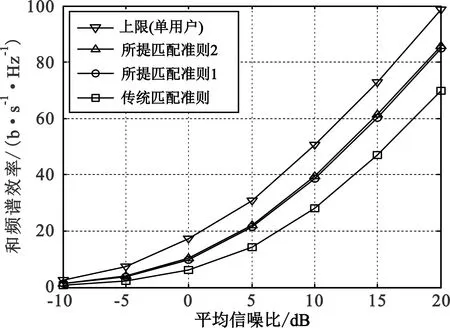
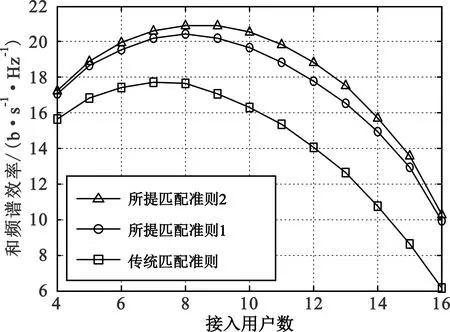
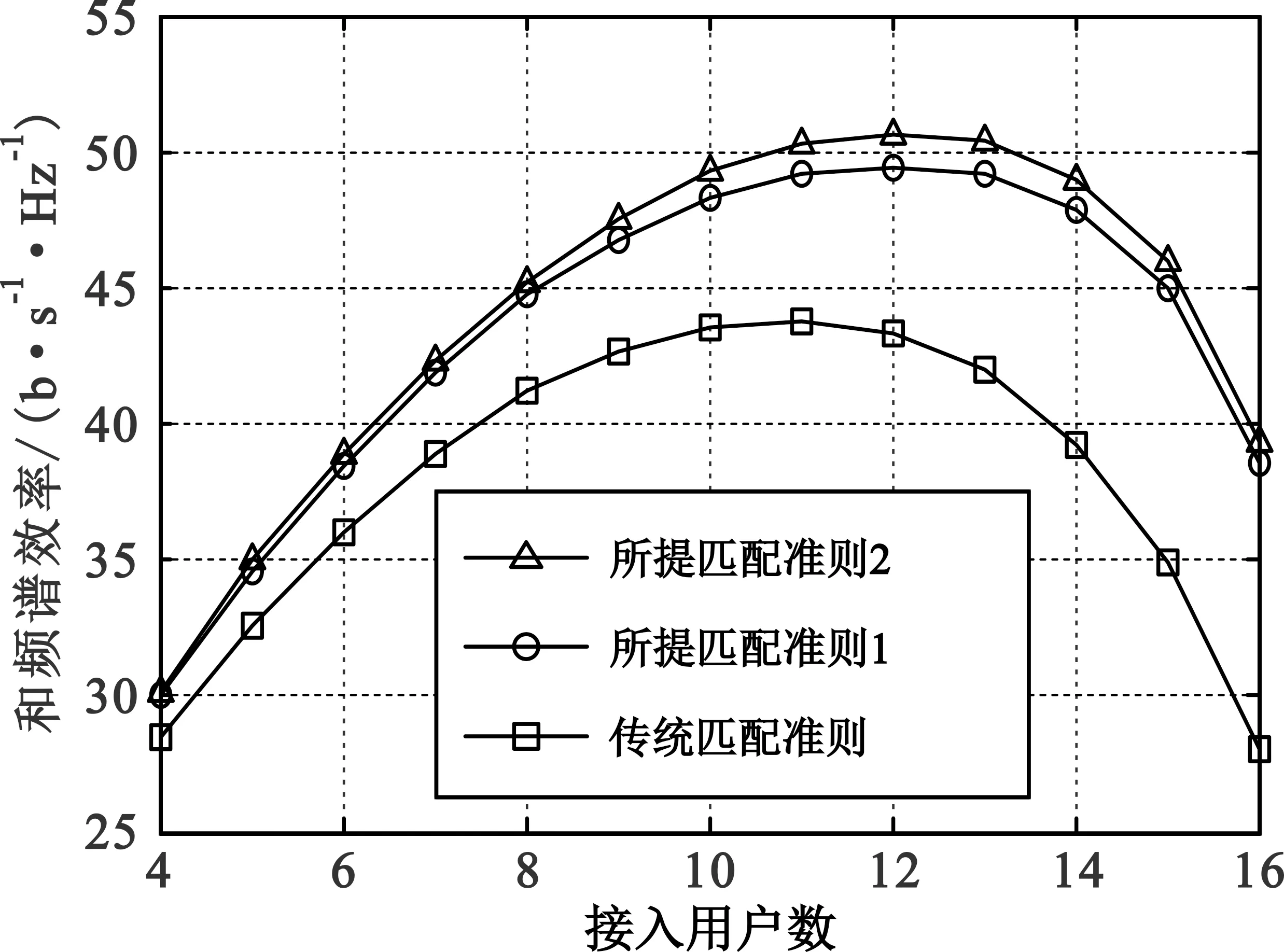
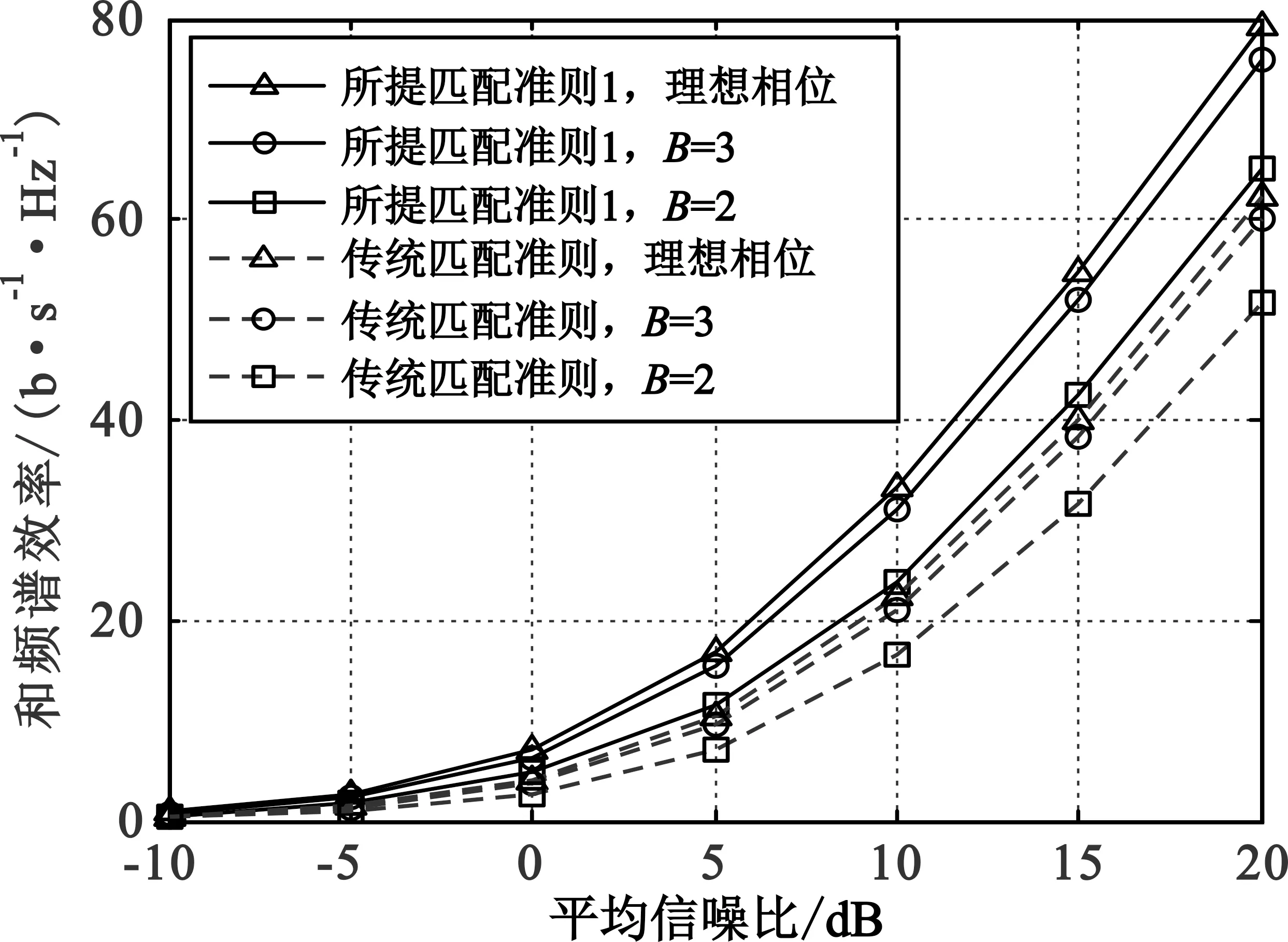
第2轮匹配。若K 设用户序号集合为U={1,2,…,K},子阵列序号集合为A={1,2,…,NRF} 第1轮匹配。首先,对所有用户,根据式(9)计算其对应的所有子阵列增益{ηk(n)|k∈U,n∈A},再从中选择具有最大值的ηk(n),将其对应的用户序号和子阵列序号分别记为k1∈U和n1∈A,即给用户k1匹配了子阵列n1。其次,对除用户k1之外的其余所有用户,从除子阵列n1以外的其余所有子阵列增益{ηk(n)|k∈U{k1},n∈A{n1}}中选择具有最大值的ηk(n),将其对应的用户序号和子阵列序号分别记为k2∈U{k1}和n2∈A{n1},即给用户k2匹配了子阵列n2……以此类推,直至为最后一个用户kK匹配了子阵列nK。 第2轮匹配。若K 匹配准则1和2的基本思想都是对每一用户在可选子阵列中选择使该用户获得最大子阵列增益的子阵列与之匹配,区别在于匹配准则1仅对用户按默认顺序来匹配最优子阵列,而匹配准则2则从全局优化角度还对用户排序。所提两种匹配准则生成的模拟预编码矩阵不再满足式(8)的块对角结构,而具有如下更一般的块稀疏结构(上标“N”表示新匹配准则): (10) 图1中的用户和子阵列匹配器根据所提匹配准则1或2实施用户和子阵列的匹配。该匹配器的输出结果决定了用户k和对应子阵列的值(k,nk),通过(k,nk)值查找到子矩阵Hnk的第k个行向量,该行向量所含各信道系数的相位即决定了式(6)中fn各元素的相位值,即移相器对相应天线的具体移相值。由此,用户k可获得对应的最大子阵列增益ηk(nk)。 与文献[11-12]类似,根据FRF在基带可得等效信道矩阵G=HFRF,对G求伪逆得 W=GH(GGH)-1。 (11) 以W各列向量的Frobenius范数为对角元构造对角矩阵Λ,则数字预编码矩阵可通过FBB=WΛ-1计算,此归一化处理保证了FBB各列的Frobenius范数都为1。由此,有 在已有实践管理与学术研究基础上,笔者认为,水生态文明建设是以水生态系统为对象,通过工程性措施与非工程性措施建设,使其满足人类社会发展需求,并最终形成一种可自我更替、完善的良性演化过程。 (12) 即满足总发射功率约束对预编码矩阵的范数要求。 本节分析比较文献[11-12]中传统匹配准则和本文所提两种匹配准则的计算复杂度。传统匹配准则的混合预编码总的计算复杂度为O(MKNRF+K2NRF)次复数乘法[12]。与传统匹配准则相比,所提两种匹配准则引入了用户和子阵列匹配处理,该处理需要根据式(9)计算ηk(n)并在一组ηk(n)中查找最大值,经分析知匹配准则1和2中该处理的计算复杂度分别为O(MK(NRF-K/2))和O(MKNRF+K2NRF)次复数加法。考虑到实际不同软硬件约束条件,单次复数乘法的计算复杂度约为单次复数加法的10~100倍。因此,匹配准则2相较于传统匹配准则增加的计算复杂度约为1%~10%,而匹配准则1的计算复杂度略低于匹配准则2。 对不同参数下基于所提两种匹配准则和文献[11-12]传统匹配准则的部分连接结构多用户大规模MIMO混合预编码性能进行仿真评估,所有用户均为单天线接收。同时,考虑到难以获得此情形的最优混合预编码方案[5,7],将相同参数条件下的K个单天线用户替换为具有K个接收天线的虚拟单用户,该虚拟单用户系统采用基于奇异值分解的数字预编码和集中式接收的性能可作为对应多用户系统的理论上限[5,13]。假设基站能获取准确信道矩阵H。 图2给出了用户数K=16时三种匹配准则与上限的和频谱效率R与信噪比P/σ2之间的关系,可以看出,在所示信噪比区域,所提匹配准则1和2分别比传统匹配准则的和频谱效率提升了25%~85%和35%~100%,提升幅度随信噪比减小而增大;在中高信噪比区域,所提两种准则相较理论上限仅有3~3.5 dB差距。 图2 Rayleigh衰落信道下和频谱效率R与信噪比P/σ2的关系(NTX=256,NRF=K=16) 图3比较了信噪比P/σ2为0 dB和10 dB时三种匹配准则的和频谱效率R与接入用户数K之间的关系,可以看出,信噪比固定时,和频谱效率都呈现出随用户数增加而先升至一定峰值再降低的特点;信噪比越低,和频谱效率峰值对应的最佳用户数越小,当P/σ2=0 dB时,所提匹配准则1、2和传统匹配准则的峰值对应的最佳用户数分别为8、8和7,前两者和频谱效率峰值分别比后者提升了约12%和17%。当P/σ2=10 dB时,三种匹配准则峰值对应的最佳用户数均为11,且前两者和频谱效率峰值分别比后者提升了约10%和15%。 (a)P/σ2=0 dB (b)P/σ2=10 dB图3 Rayleigh衰落信道下和频谱效率R与用户数K的关系(NTX=256,NRF=16) (13) 图4给出了用户数K=16时三种匹配准则与上限的和频谱效率R与信噪比P/σ2之间的关系,从中可以看出,在所示信噪比区域,所提匹配准则1和2分别比传统匹配准则的和频谱效率提升了20%~75%和25%~85%,提升幅度仍随信噪比减小而增大;所提两种准则相较理论上限仅有2.5~3 dB差距。 图4 S-V信道下和频谱效率R与信噪比P/σ2的关系(NTX=256,NRF=K=16 ) 图5比较了信噪比P/σ2为0 dB和10 dB时三种匹配准则的和频谱效率R与用户数K之间的关系,其中和频谱效率随用户数增加呈现的变化规律与图3类似。当P/σ2=0 dB时,所提匹配准则1、2和传统匹配准则的和频谱效率峰值对应的最佳用户数分别为8、9和7,前两者的峰值分别比后者提升了约15%和18%。当P/σ2=10 dB时,所提匹配准则1、2和传统匹配准则的和频谱效率峰值对应的最佳用户数分别为12、12和11,且前两者和频谱效率峰值分别比后者提升了约13%和16%。 (a)P/σ2=0 dB (b)P/σ2=10 dB图5 S-V信道下和频谱效率R与用户数K的关系(NTX=256,NRF=16) 图6 Rayleigh衰落信道下量化信道相位对和频谱效率R的影响(NTX=256,NRF=K=16) 从以上三组仿真可以看出,对Rayleigh衰落和S-V两种典型信道场景,在给定基站天线数和射频链路数条件下,无论固定接入用户数改变信噪比,还是固定信噪比改变接入用户数,本文所提两种匹配准则较传统匹配准则对系统和频谱效率均有显著改善,而与理论上限差距较小,且有限位的B比特移相器对所提准则的性能影响较小。 本文针对部分连接结构的多用户大规模MIMO混合预编码系统,提出了基于最大化用户子阵列增益匹配准则的模拟预编码方法,通过提取每个用户对应子阵列的信道相位信息生成该用户的模拟预编码向量并进而构造整体的模拟预编码矩阵。复杂度分析和典型场景下仿真表明,相较于传统基于固定匹配准则的混合预编码,基于所提匹配准则的混合预编码在几乎不增加计算复杂度的前提下能显著提升系统的和频谱效率,提升幅度随信噪比减小而增大,且对有限精度的相位量化较为鲁棒。考虑到5G和未来无线通信的绿色节能需求,大规模MIMO系统的平均发射功率通常较小,因此,所提方案在实际应用时将更加凸显优势。2.5 数字预编码矩阵求解
3 计算复杂度分析
4 仿真分析
4.1 独立同分布Rayleigh衰落信道条件下的和频谱效率性能
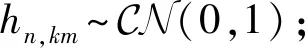
4.2 Saleh-Valenzuela信道条件下的和频谱效率性能

4.3 不同相位量化精度对和频谱效率的影响
5 结束语
