恒温差热式流量计分段PID控制的仿真与实验
2021-09-29张夷非魏勇余厚全陈强刘国权贺飞
张夷非,魏勇,余厚全,陈强,刘国权,贺飞
(1.长江大学电子信息学院,湖北荆州434023;2.中国石油集团测井有限公司生产测井中心,陕西西安710077)
0 引 言
传统的涡轮流量计由于需要一定的启动排量,无法满足低产液油井流量检测需求。热式流量计无可动部件,对低速流动流量变化敏感,可靠性高,为低产液油井的流量检测提供了一种可行的解决方案[1]。热式流量计分为恒温差热式流量计和恒功率热式流量计,恒温差热式流量计的响应时间优于恒功率热式流量计,且对低流量流体具有更高的测量精度[2]。因此,研究恒温差热式流量计对解决低产液油井微小流量的检测难题具有重要意义。
恒温差热式流量计的检测原理为当流体的流量变化时,动态调整加热器功率,保持传感器之间温度差稳定,建立加热器功率随流量变化的单调关系,将流体流量的检测转换为加热功率的测量。因此,该检测方法对恒温差控制算法的要求较高。
本文介绍了恒温差热式流量计的测量原理,对实际流量检测系统进行建模,针对建立的模型分别按增量式数字比例积分微分控制[3](PID控制)和分段增量式数字比例积分微分控制(分段PID控制)进行仿真与实验研究。研究结果表明,相比PID控制,分段PID控制能够减少恒温差热式流量计的响应时间,提高测量精度,更适合作为恒温差热式流量计的控制算法。
1 测量原理与仿真分析
1.1 测量原理
热式流量计测量的物理基础是热扩散[4],其中,恒温差热式流量计测量时,将测温探头和测速探头浸入被测流体中,测温探头放置在流体上游,测速探头放置在流体下游,且与测温探头保持一定距离。其中,测速探头由温度传感器和加热器组合而成(见图1)。

图1 恒温差热式流量计示意图
在测量过程中加热器接通电源加热。在热平衡状态下,根据传热学研究及Kramers[5]的换热公式,加热器功率和流体流速满足关系[6]
P=(k1+k2v0.5)(Th-Te)
(1)
式中,P为加热器功率,W;v为流体流速,m/s;Th为测速探头测量的加热器温度,℃;Te为测温探头测量的环境温度,℃;当加热器结构和被测流体物性一定时,k1、k2均为常数。若保持测速探头加热器温度Th与测温探头环境温度Te之差ΔT不变,加热器功率与流体流速的幂成正比,这种热式流量测量方法称为恒温差法。
1.2 恒温差控制模型分析
恒温差控制模型见图2。输入端将温度差ΔT转换为温差电压Uc;根据控制器比较温差电压Uc与预设温差电压Us的电压差ΔU,输出合适的加热电压U;电加热机构调节加热功率P,最终形成反馈调节,使温度差ΔT保持稳定,实现恒温差的调节。

图2 恒温差控制模型
对于图2中控制器与电加热机构断开的开环系统,系统实际输入1个阶跃加热电压信号Ui,即可得到其温差的阶跃电压响应。在常温常压的近似封闭井筒环境内,将传感器置于静水中,分别施加恒定加热阶跃电压信号Ui=1.0,1.5,…,3.0 V后的系统阶跃响应见图3。

图3 电加热机构的阶跃响应
图3中曲线反映实际电加热机构在不同阶跃加热电压的激励下,随时间变化的温差电压。通过模拟仿真发现,用一阶惯性+纯滞后环节与该实际过程最佳拟合,其s域的传递函数为
(2)
式中,Kg为静态增益系数,无量纲;Tp为时间常数,无量纲;Td为滞后时间,s。实际工程应用中,可以根据被控对象在阶跃响应下的输出响应曲线确定其近似传递函数。在MATLAB软件中导入不同加热电压下的响应曲线,通过系统识别进行统计建模,得到传递函数参数Kg=0.000433、Tp=31.079、Td=9.1,电加热机构的系统传递函数表示为
(3)
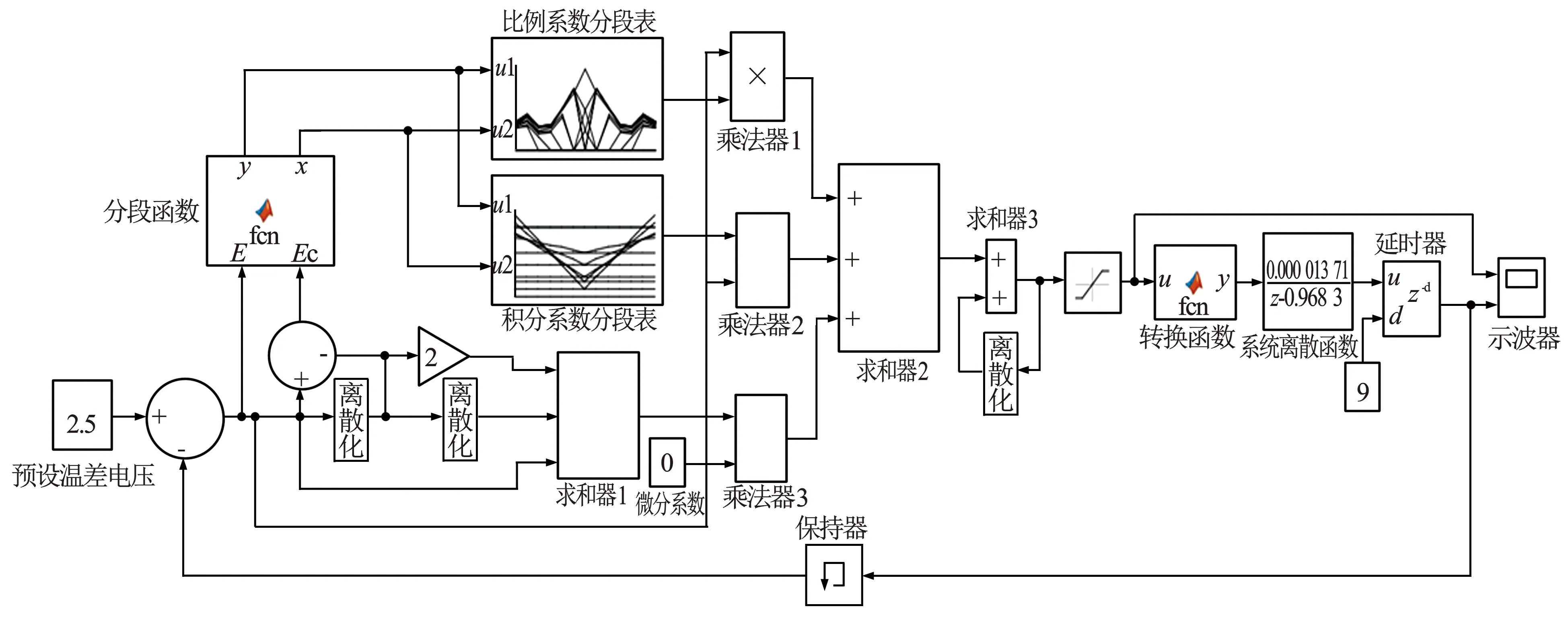
图4 PID控制仿真系统
2 恒温差控制算法设计
在恒温差条件下,式(1)确定加热器功率P与流体流速v的关系。为了根据加热器的实时加热功率来检测当前流体流速,必须维持温度差ΔT恒定,这对恒温差控制算法提出了较高要求。
2.1 PID控制算法
温度控制系统一般采用数字PID控制算法,其中增量式PID控制算法能减少存储单元,避免输出产生大幅度误差,被广泛应用于工业控制,其算式
ΔN=n(j)-n(j-1)=Kp[E(j)-E(j-1)]+
KiE(j)+Kd[E(j)-2E(j-1)+E(j-2)]
(4)
式中,j为采样序号,j=1,2,…;ΔN为控制器2次输出n(j)、n(j-1)的增量;E(j-2),E(j-1),E(j)分别为(j-2)、(j-1)和j时刻得到的系统偏差;Kp为比例系数,增大该系数可以加快系统的响应速度、降低稳态误差,但过大会导致系统振荡或发散;Ki为积分系数,增大该系数可以减小系统的调节时间,但过大会导致系统不稳定;Kd为微分系数,增大该系数可以抑制偏差变化,但过大会延长调节时间,降低抗干扰能力[7]。
2.2 分段PID控制算法
传统PID控制算法理论成熟,结构简单,但要求被控对象具有合适的数学模型。实际上许多控制对象无法用精确的数学模型描述,具有大时滞、非线性等特点,采用单一PID参数调节不容易达到理想的控制效果[8]。根据控制对象的实际情况以及偏差的大小,在不同的控制阶段给定不同的PID调节参数,这样既可以增加响应速度,超调量也不会太大,这就是分段PID的控制思想。
2.3 恒温差控制算法仿真
为了研究PID控制算法及分段PID控制算法在静水中的调整效果,利用Simulink软件模块进行恒温差流量控制仿真。根据式(3),若系统采样时间为1 s,则相应的数字离散系统传递函数为
(5)
根据传递函数建立的PID控制系统见图4。该系统预设的温差电压为2.5 mV,信号延时设置为9 s,仿真时间设置为300 s。由于该恒温差控制系统分辨率高,对外界扰动敏感,偏差变化加速度不具有参考性,故舍弃微分参数。常规PID控制参数可根据Ziegler-Nichols参数整定方法(Z-N法)确定比例系数Kp为0.68,积分系数Ki为0.03[9]。而分段PID控制算法采用不同的系统偏差E和系统偏差变化率Ec作为调整的输入控制变量。
(1)如果E为正且Ec也为正,或者E为负且Ec也为负,表明存在偏差且偏差还在继续加大。为了确保系统有较好的追踪性能,Kp在|E|值最大和|Ec|值很小时取最大值,并随着|E|的减小和|Ec|的增大而适当减小;Ki在|E|值最大和|Ec|值最大时取最大值,并随着|E|的减小和|Ec|的减小而适当减小。
(2)如果E为正且Ec为负,或者E为负且Ec为正,表明尽管存在偏差,但偏差正在减小。随着|E|值的增大和|Ec|的增大,Kp的取值减小,抑制变化的力度减弱;Ki在|Ec|较小且|E|值大时取较大值,并随着|E|的减小和|Ec|的增大而减小,以便更好消除累积偏差。
比例系数Kp参数分段表见表1,积分系数Ki参数分段表见表2。表中按系统偏差E和偏差变化率Ec分为不同区间,给定了该区间参数参考值。

表1 比例系数Kp参数分段表
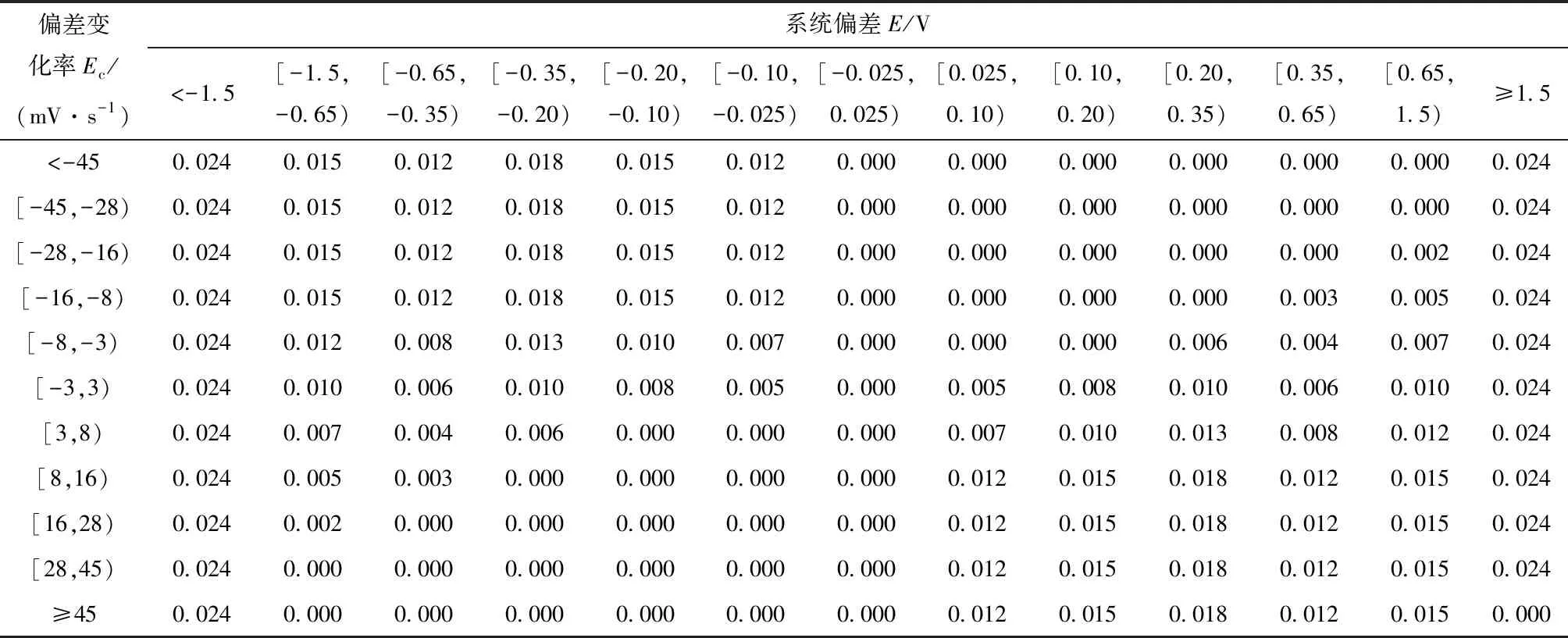
表2 积分系数Ki参数分段表

图5 温差电压控制曲线对比
根据2种控制算法,基于MATLAB软件仿真的恒温差控制系统的温差电压变化见图5。根据图5中的2条曲线可以计算常规PID控制和分段PID控制的恒温差系统动态性能指标(见表3)。通常来说,上升时间tr评价系统的响应速度,超调量σ评价系统阻尼程度,调节时间ts反映响应速度和阻尼程度综合性指标[3]。由表3可见,分段PID控制无论是调节时间还是上升时间,均快于常规PID控制,超调量均不到0.5%。仿真结果表明,分段PID控制算法具有响应速度快、稳定性高的优点,在热式质量流量计的恒温差控制中具有实用价值。

表3 恒温差系统动态性能指标
3 恒温差流量检测控制实验
3.1 流量测试装置
基于热式流量计的检测原理,设计并搭建了一套井下井筒流体模拟系统(见图6),其中模型井内径为200 mm。水泵抽出流体(水),经标准流量计计量后,从模型井底部流入井筒。当模型井中液面高于溢出孔时,流体在重力作用下流回水箱,完成循环。系统正常循环时,流体从下至上流经热式流量计,根据水泵阀门的开合程度,流体流速会发生变化,并显示在标准流量计上。因此,可根据流体流速和热式流量计功率的关系来评价系统响应是否满足需求。

图6 井下井筒流体模拟系统
3.2 零流量测试实验
将水箱注满水,与测试环境等温。将水泵开至最大流量,循环10 min后关泵。这时恒温差流量计开始记录零流量时的温差电压和加热电压的变化。为了减小外界干扰影响,对采集的数据进行10 s的平滑滤波处理,得到零流量温差电压和加热功率曲线见图7。

图7 零流量温差电压和加热功率曲线
实验数据表明,在流体为全水、流速为0的情况下,上升时间tr约为60 s,超调量σ约为10%。与仿真结果对比,实测结果上升时间tr基本不变,超调量σ有所增大。
3.3 等梯度流量实验
为了评价采用分段PID控制算法的恒温差热式流量计对不同流量的响应特性,根据标准流量计上的流量读数,调整控制水泵,使进入井筒的流量分别为0.7、0.6、0.5、……、0 m3/h,每隔300 s调整一次流量,数据采样率为1 s,预设维持的恒定温差电压为2.5 mV。实验结果见图8(a),加热器功率随流量变化分布曲线见图8(b),并计算相应流量端加热器的平均功率
(6)
式中,Ut为当前时刻采样得到的加热电压值,V;R为加热器电阻,约为22 Ω。实验结果表明,在内径为200 mm的井筒内采用恒温差分段PID控制算法,可以在0~0.7 m3/h流量范围内,清晰分辨0.1 m3/h的流量变化。
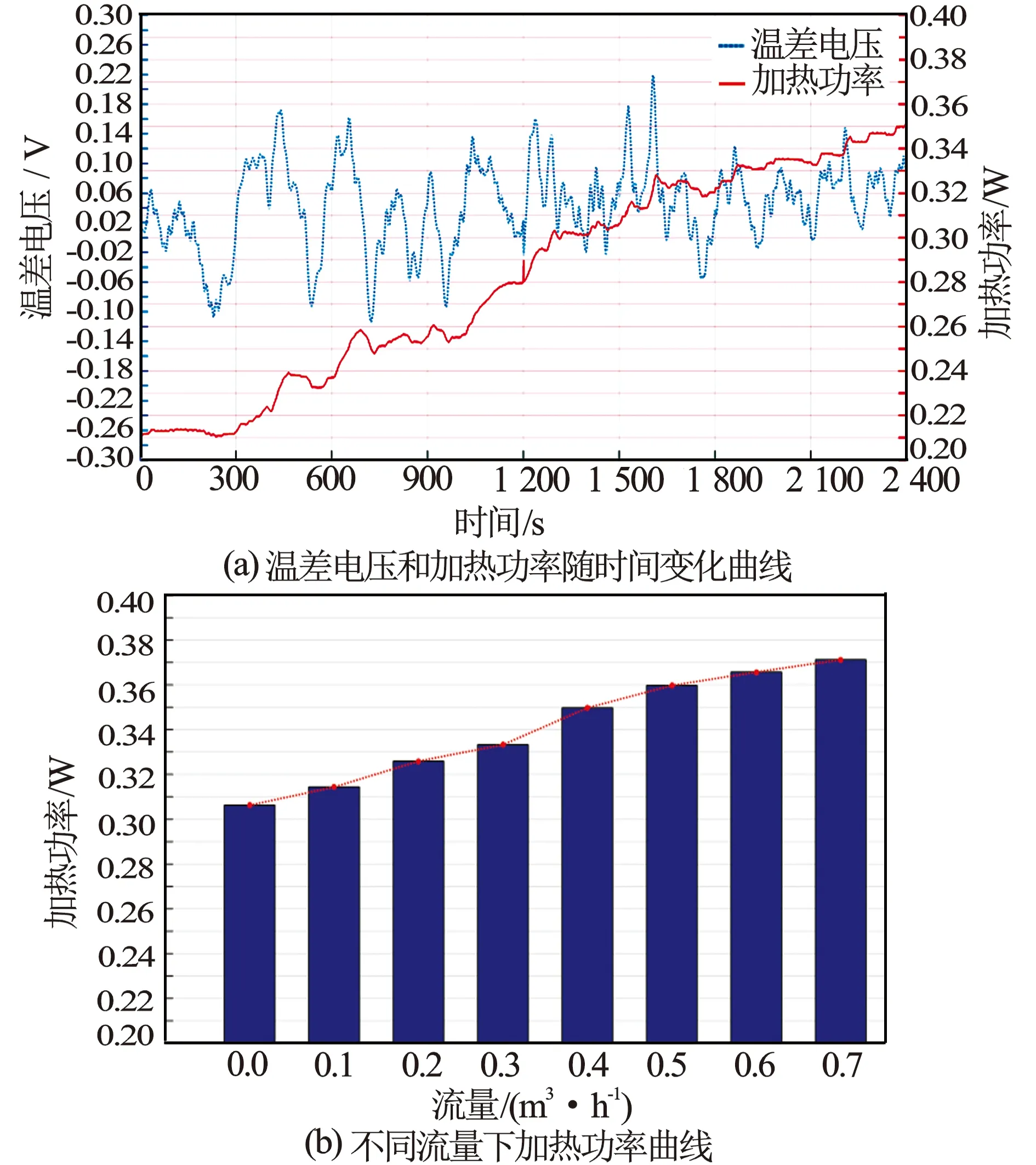
图8 等梯度流量实验数据
4 结 论
(1)由恒温差热式流量计的检测原理,根据实际模型的测量数据系统建模结果表明,恒温差热式流量计实际模型近似电加热机构,可用于井下微小液相的流量检测。当仪器系统达到热平衡状态后,其加热器输出功率可反映当前被测流体流量。
(2)通过实际模型验证了恒温差控制算法,结果表明,分段PID算法更适合于恒温差热式流量计的控制算法,相较常规PID控制算法,分段PID控制算法能够缩短仪器响应时间。
(3)实际模型井筒的流量实验数据证实了分段PID控制算法在恒温差热式流量计控制中的可靠性,采用分段PID控制的恒温差热式流量计响应速度快,流量检测分辨率高,满足低产液井的流量检测需求,为解决井下微小液相的流量检测难题的实现提供了一种可行的技术手段。
