等距线法在平面凸轮磨削中的应用
2021-09-28张新宁聂坤关振浩
张新宁,聂坤,关振浩
陕西汉江机床有限公司 陕西汉中 723003
1 序言
在加工凸轮时,往往是用户提供凸轮的升程、回程数据,以及每两个相邻点相对于凸轮中心的旋转角度、凸轮的基圆半径和滚子半径等数据,根据这些数据来计算实际凸轮上的对应点坐标。一般情况下,大多采用曲线拟合的方法来计算,而且在曲线拟合的过程中,可能会出现一些奇异点,这就需要反复调整拟合参数,进行大量重复计算,并多次对拟合数据进行校核,耗时多、工作效率低。为了解决这些问题,采用了多边形等距线的计算方法,大大提高了数据的计算效率。
2 凸轮模型构建
2.1 凸轮升程、回程数据和其他参数
凸轮的升程和回程数据基本上都是以文本数据文件的格式提供,一般分为两个文本文件,一个是升程,另一个是回程。通过整合两个文件中的数据,可形成一个完整的升程、回程数据曲线(见图1)。

图1 凸轮的升程、回程数据曲线
其他参数包括:基圆半径R=16mm,滚子半径r=9.525mm,相邻数据点角度△C=1°。由于凸轮升程数据中不包含凸轮的休止期,所以要根据升程数据和凸轮参数情况,补充凸轮休止期数据。
2.2 滚子中心及凸轮上点的坐标计算
本文主要分析研究对心直动滚子从动件盘形凸轮。图2为凸轮和滚子之间的运动结构,滚子只作垂直往复运动,凸轮绕基圆圆心作回转运动。为了研究方便,将其看作凸轮和滚子之间的相对运动,即凸轮静止不动,而滚子绕凸轮的基圆圆心作旋转运动,同时还沿凸轮法线方向作升程、回程运动。
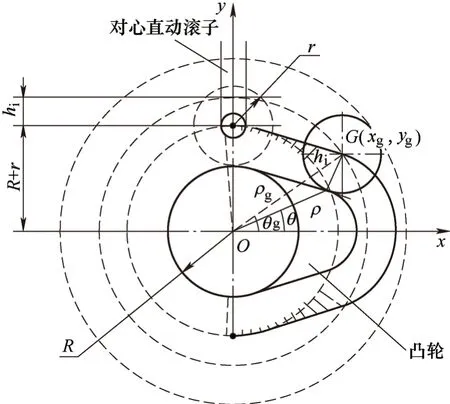
图2 凸轮和滚子之间的运动结构示意
设凸轮某一点上的升程高度为hi,凸轮中心到滚子中心的距离为ρg,此时凸轮旋转过的角度为θg(凸轮在最大升程点处θg=0°),滚子中心坐标为G(xg,yg),则有
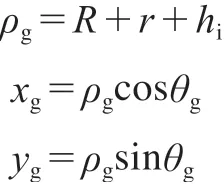
由凸轮的升程数据,通过计算可以得到与之相对应的滚子中心点坐标值。把相邻的滚子中心点连线,得到滚子移动的封闭曲线。再用滚子移动封闭曲线作对应的内推等距线,等距距离为d,得到凸轮的近似曲线,这就是凸轮参数计算、磨削的基本思想。
在图2中,设由推等距线计算得到的凸轮上点的坐标为(x1,y1),那么凸轮上点的极径ρ和极角θ为
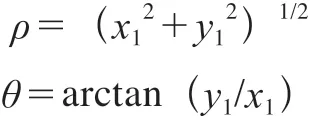
2.3 磨削时砂轮中心的计算
计算砂轮中心坐标和计算凸轮上实际点的坐标方法相同,区别在于需要作滚轮中心轨迹曲线的外推等距线,外推等距线的距离为D/2-r,其中D为砂轮的直径。
但在实际计算中采用作凸轮实际曲线的外推等距线的方法,而不采用滚子中心轨迹曲线的外推等距线。这是因为如果砂轮直径D小于滚子直径(D<2r),外推等距线就变成了内推等距线,容易产生思维上的混乱。
2.4 凸轮磨削模型和磨削方法
凸轮磨削时并不是按照上述位置坐标来移动砂轮的,实际工况如图3所示。

图3 凸轮磨削实际工况
凸轮磨削的工作原理如图4所示,凸轮轴在机床上进行旋转运动(数控机床上定义为C轴),砂轮架在机床上作前后往复运动(数控机床上定义为X轴)。因此,砂轮中心的坐标要换算到机床上的X轴的位置坐标。如果把凸轮中心处设为X=0,砂轮接触凸轮最大点处的C轴角度为0°的话,编程就可以大大简化。
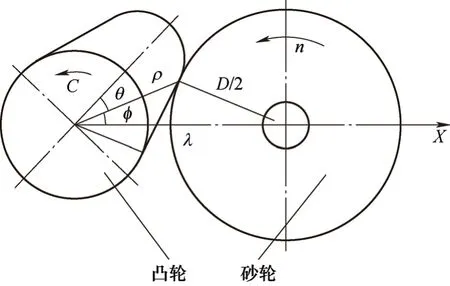
图4 凸轮磨削原理示意
设砂轮中心坐标为(xs,ys),则砂轮中心到凸轮中心的距离λ=(xs2+ys2)1/2,此时凸轮旋转过的角度为θ+φ。由余弦定理可得
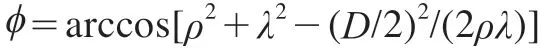
数控系统中编程语句为:
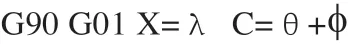
一般情况下,凸轮磨削不是一次进刀完成的,需要多次进刀磨削,这取决于实际加工余量。假如需要两刀或者三刀来完成,就需要在计算砂轮中心坐标点的等距线时,对算法进行修正。如果改用每次磨削的进刀量来计算,则需要把当前进刀后剩余的磨削余量计算出来。设δ是本次磨削余量大小,则当前砂轮中心移动轨迹曲线就是凸轮曲线的外等距线,且等距距离为δ+D/2。
图5 是凸轮多次进刀磨削的模拟效果示意,模拟机器为西门子828D sl数控系统。为使图片效果表现得更清晰,本例中每次进刀量设置较大,不代表实际磨削效果。
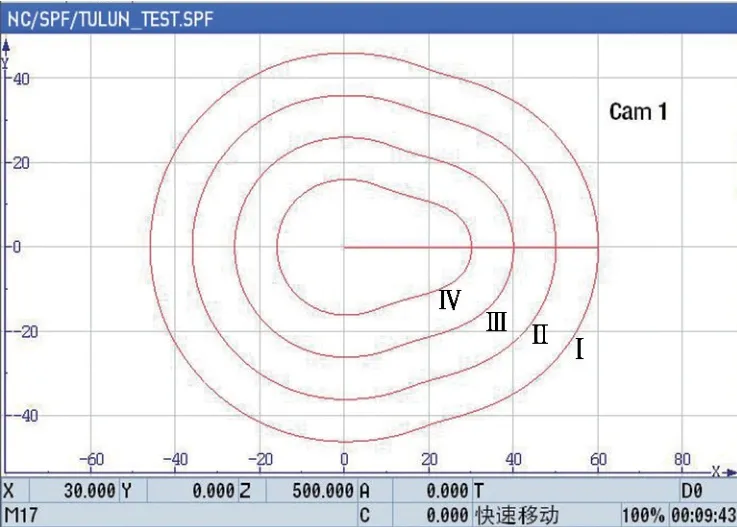
图5 凸轮多次进刀磨削模拟
在图5中,最外侧的等距线Ⅰ是凸轮磨削之前的形状;Ⅱ是第一刀磨削后的凸轮形状;Ⅲ是第二刀磨削后的凸轮形状;最内侧曲线Ⅳ是磨削完成(第三刀磨削)后的凸轮形状。
3 等距线的原理及计算
3.1 外推等距线
外推等距线一般分为两种情况:曲线上凹和曲线上凸,如图6所示。设有不在同一条直线上的三个点A、B、C,坐标分别为A(xa,ya)、B(xb,yb)、C(xc,yc),且xa>xb>xc。连接BA和BC,作∠ABC的内角平分线BP,BP向量角为α。分别作AB、BC的平行线,平行线的方向取决于等距线的方向,并且使得平行线之间距离为d。AB、BC的平行线相交于点B1,需要计算的就是点B1坐标值(x,y)。
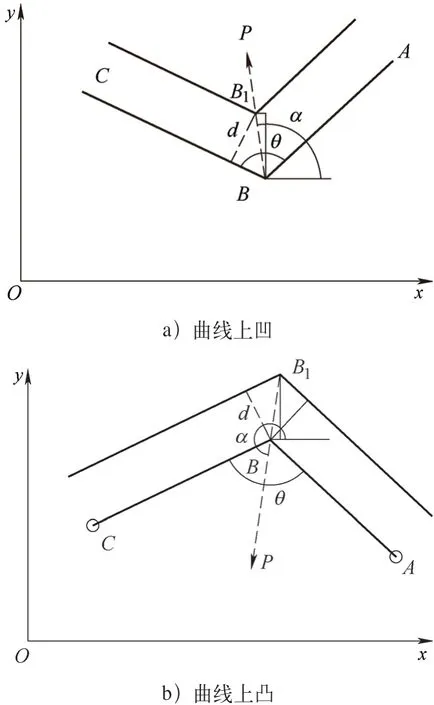
图6 外推等距线示意
对于上凹的情况
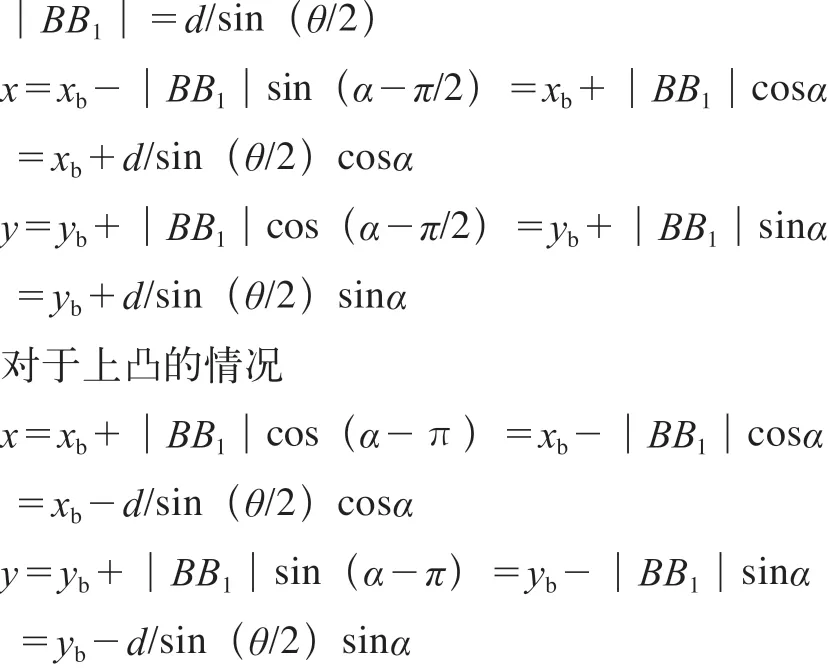
3.2 内推等距线
和外推等距线算法相似,计算可得内推等距线对应点的坐标。
对于上凹的情况
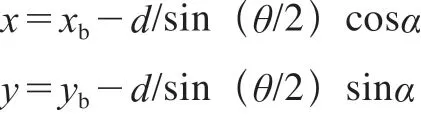
对于上凸的情况
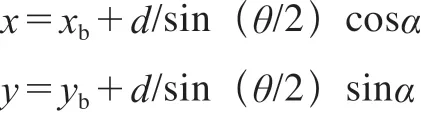
3.3 封闭曲线的等距线
在计算封闭曲线的等距线时,第一个点对应的等距线位置需要第二个点和最后一个点坐标来计算,最后一点处的等距线位置需要倒数第二个点和第一个点坐标来计算。
由于凸轮的第一个点选取的是凸轮升程的最大点,所以第一个点的等距线位置计算就变得比较简单。设hmax为凸轮升程的最大值,则凸轮第一个点对应的B1点坐标x=(R+r+hmax)+d,y=0。
4 推等距线对实际凸轮坐标的影响
由于推等距线的前提条件是连续的坐标点连接起来的线段,不可避免的问题是磨削后的凸轮外缘是否光滑。如果凸轮升程曲线上采集的点数较少,就会明显造成凸轮外缘不平滑,使得磨削的凸轮报废或不合格;但当采集的点数足够多时,凸轮外缘平滑情况就会得到明显好转。
实际生产中,由于凸轮升程曲线上的点是由用户提供的,数量可能不够多,因此计算时需要添补一些点,使得应用点足够多。大多情况下,可以采用三次样条插值或者其他插值方法获得。
5 结束语
结合本文中的分析计算结果,可以用VB、VC或者其他编程软件进行编程计算,得到砂轮位置坐标和头架旋转角度,并直接输出为数控系统可接受的加工程序文件。通过现场试验和磨削工艺调整、控制,达到了满意的磨削效果。
