基于全年动态光环境模拟条件的穿孔金属表皮参数对室内天然光环境效果的影响
2021-09-28刘宇波刘彬艳邓巧明
刘宇波,刘彬艳,邓巧明
(华南理工大学建筑学院,广东 广州 510640)
引言
穿孔金属表皮是在金属表皮的基础上发展而来,经穿孔、冲孔、编织、焊接、拉伸等工艺,形成具有孔洞的金属表皮材料,常与其他表皮组合形成复合表皮用于各个类型的建筑之中,如教育建筑、博物馆、办公楼、住宅等,如图1所示。

图1 穿孔金属表皮案例照片Fig.1 Photo of buildings with perforated metal skin
设计师常出于形式的考虑对穿孔金属表皮孔径和孔隙率进行选择,忽略了穿孔金属表皮本身在隔热和采光方面的潜力,如图2所示。过小过密的孔洞,遮阳效果越好,但是室内自然光效果势必会不佳;而孔洞过大,又会造成直射光进入室内,遮阳效果不佳。本文主要结合国际上新的动态采光指标,研究穿孔金属表皮的设计参数如穿孔率和孔径的变化对建筑空间天然采光效果方面的影响(图3)。
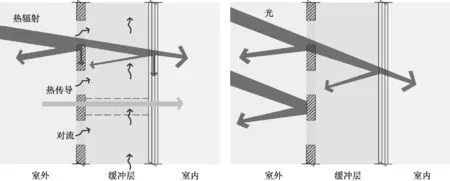
图2 穿孔金属表皮在隔热和采光方面的潜力Fig.2 The potential of the perforated metal skin for heat insulation and lighting
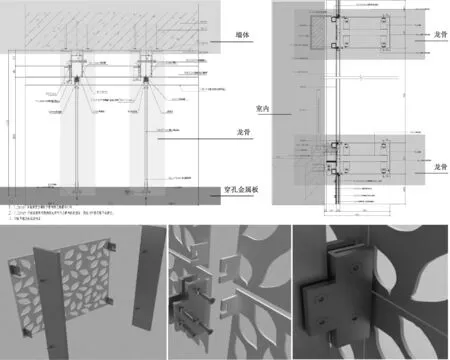
图3 穿孔金属表皮构造大样Fig.3 Structural details of perforated metal skin
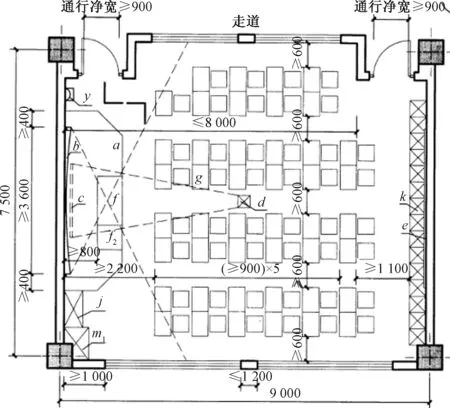
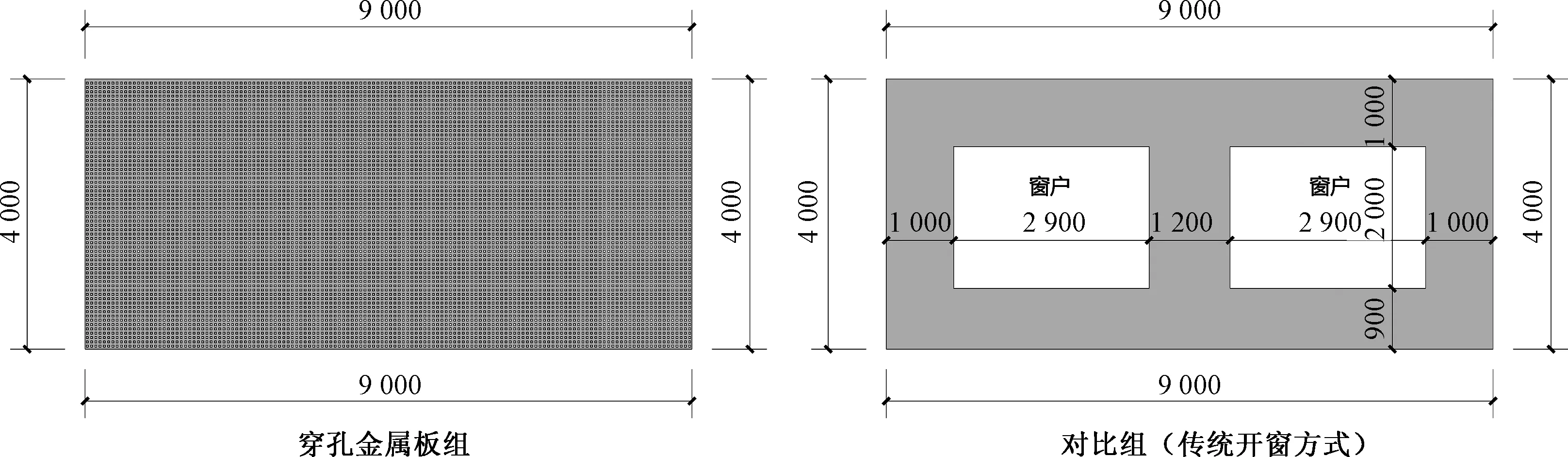
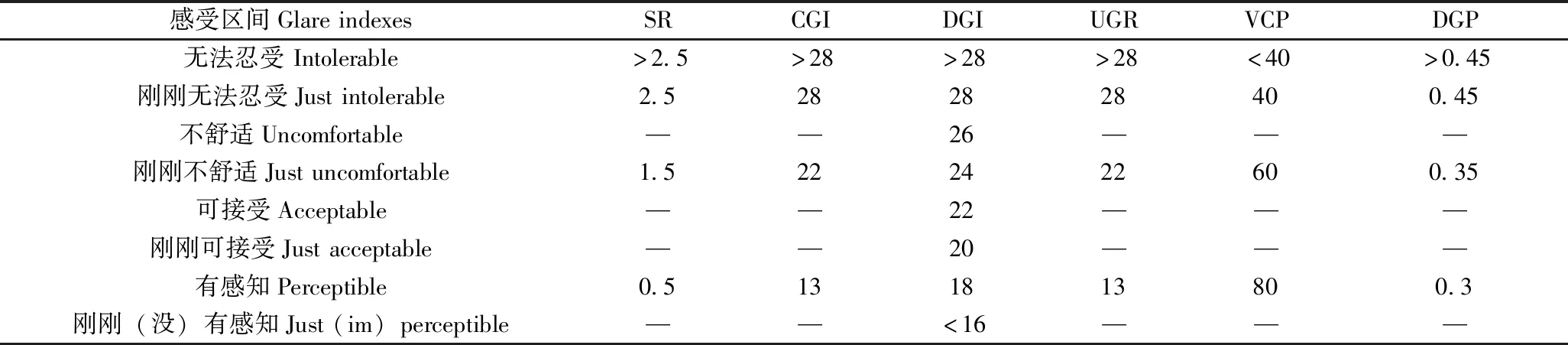
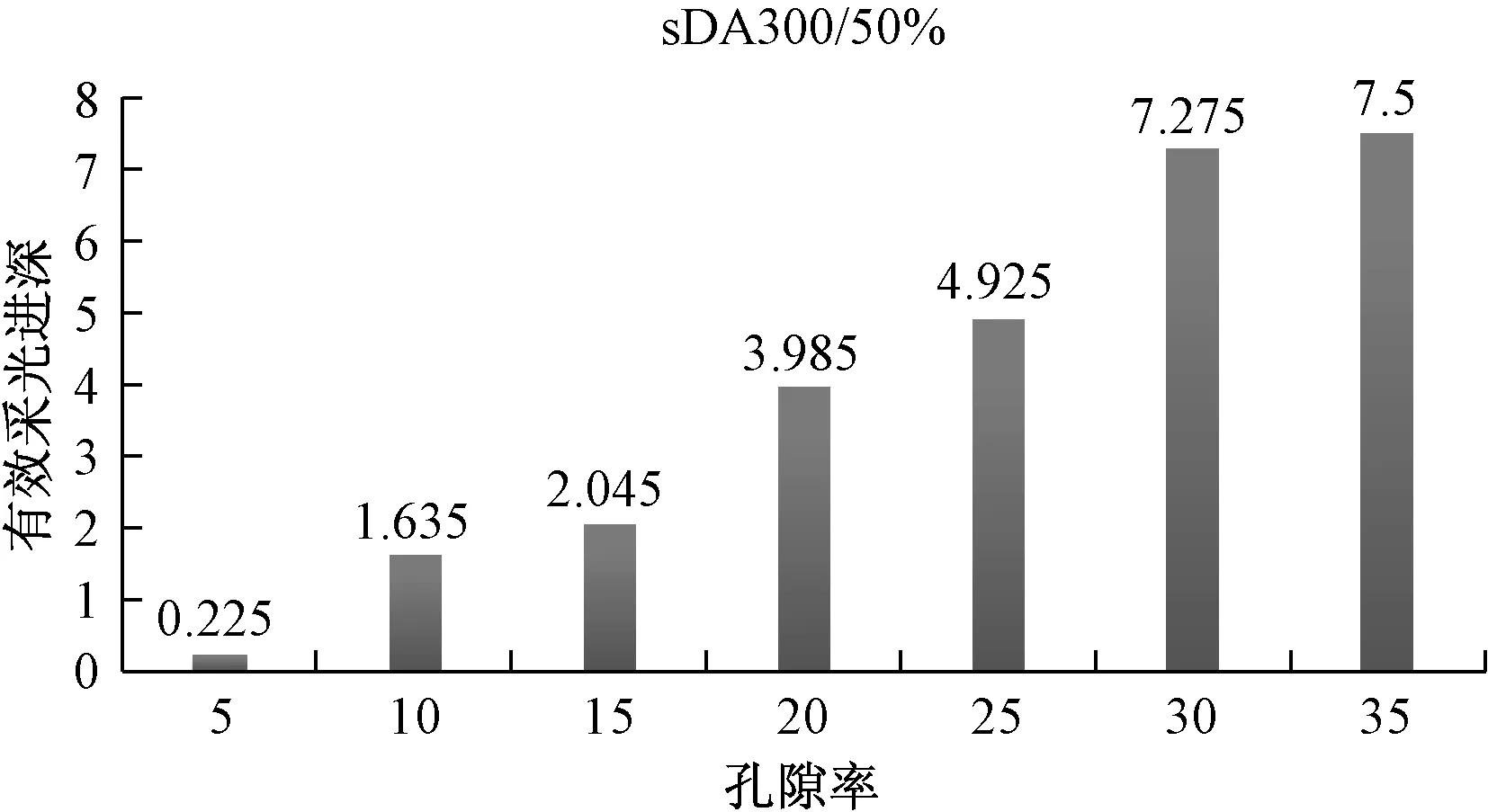
我国目前的采光标准《建筑采光设计标准》中以采光系数DF来制定,但是DF是有很多缺陷的,仅表示全阴天情况下的静态采光指标,不能反映地域性光气候特征、立面朝向等[1]。国外新发展起来的动态自然光评价标准UDI(有效全自然采光时间百分比),是由Nabil和Mardaljevic提出的概念来取代现有规范标准中单一值方法[2]。sDA300/50%用来表示空间所有照度计算点中有多少百分比的计算点在一年中(指空间占有时间,按一天10 h计,即1 825 h)可以超过50%的时间仅在自然光照射下就达到300 lx[3]。该指标是2007年由北美照明工程学会(IESNA)发起,在美国多家知名研究机构和高校的研究人员的共同努力下,历经6年的时间开发而成[4]。研究人员将300 lx作为衡量空间日光充足性的照度阈值,超过50%的空间能达到300 lx被认为是可以接受的,并且sDA300/50%于2012年已被IESNA作为采光衡量标准发布[5]。对不舒适眩光的评估方法有很多种,如Hopkinson 和 Chauvel 提出的DGI和CIE 推荐使用统一眩光值UGR。本文结合DF、100 国内已有大量的穿孔金属表皮建筑建成案例,但是研究穿孔金属表皮对室内空间天然采光效果影响的较少,对于穿孔金属表皮设计参数的研究探索就更少。本文利用动态模拟软件Daysim[6],针对室内天然采光效果,对穿孔金属表皮的设计参数如穿孔率、孔洞孔径,结合统计学分析,作出初步的探索,以期对未来的穿孔金属表皮参数选择有借鉴意义。 一般来说教室、办公室、图书馆被认为是最需要采光的空间类型[3]。笔者团队长期从事教育建筑研究,所以选取教室作为设计研究对象。根据设计规范要求以及建筑资料集案例提取总结出普通教室的标准室内单元,模型尺寸如图4所示,房间内各表面反射率及窗玻璃透射率见表1,用于后文的设计模拟。 图4 教室模型单元(国家建筑标准设计图集(11J934-2)——中小学校场地与用房)Fig.4 Classroom model (National Architectural Standard Design Atlas (11J934-2)—— Primary and Secondary School Site and Room) 表1 教室材料光学参数Table 1 Optical parameters of classroom materials 本文选择参数化建模分析,使用rhino及grasshopper程序,grasshopper可以实现输入相应参数直接生成模型。在grasshopper中将穿孔率和孔径设置为输入参数,可以实现随时变化参数输出模型。然后将模型导入到eco中,进行daysim的采光模拟运算;并将结果导入到统计分析软件SPSS进行数据分析。 为了比较孔隙率和孔径两种参数分别对室内采光效果的影响,在rhino里可以设置一个参数固定不变,等距变换另一参数,来建立穿孔金属表皮模型。Grasshopper结构图如图5所示,以期研究两个参数分别对室内光环境效果的影响。但由于当孔径越小,穿孔率越大时,模型孔洞过多会导致运算复杂,故运算的孔径范围选择为35~78 mm,穿孔率选择范围为常见的5%~35%。两两组合有55组表皮模型,参数见表2。并加入与之对比的模型,采用传统采光方式开窗,窗高2 100 mm,宽2 900 mm,窗间墙1 200 mm,窗台900 mm高。金属穿孔立面与传统采光方式开窗立面对比如图6所示。 图6 金属穿孔立面与传统采光方式开窗立面对比图Fig.6 Metal perforated facade and traditional window facade comparison 表2 55组穿孔金属表皮孔径和孔隙率Table 2 The pore size and porosity of 55 groups of perforated metal skin 图5 Grasshopper结构图Fig.5 The Grasshopper structure diagram 将55组模型导入到Daysim进行采光模拟。 表3 daysim里参数设置Table 3 Parameter settings in the daysim 续表3 55组穿孔金属板模型加一组对比模型,分别按照六个指标进行数据分析,如表4中柱状图所示。同一种颜色表示相同孔隙率,从左到右孔径由小到大,最后一个为对比组。 表4 六种指标与孔隙率、孔径关系柱状图Table 4 Six metrics are related to porosity and pore diameter 由表4可以看出,对比组的 DF、sDA300/50%、UGR、DGI 值均大于穿孔金属表皮组。其中 DF 为 6.5%,sDA300/50%为 100%,说明在没有穿孔金属表皮时,普通教室内部整体照度值较高,但同时 UGR、DGI 值也较高,分别为 27.2 和 25.3,根据表5所示,属于眩光不舒适范围。且其均匀度值属于最低,说明室内照度虽高,但属于近窗处过亮而远窗处过暗,造成了均匀度低的问题,而且100 表5 常见眩光指数评价范围Table 5 Evaluation range of the common glare index 如表4所示,六个指标均随着孔隙率大小的变化而变化。DF、sDA300/50%、UGR、DGI 随着孔隙率的增大先增大。而有效天然采光 UDI 指标随着孔隙率的增大先增大,到孔隙率为15%时达到最大,后随着孔隙率的增大反而减小。而均匀度则在孔隙率为10%时达到最大,在15%时次之。 而孔径对其中四个指标(DF、100 综上所述,对比组较穿孔金属表皮组虽整体值高,但容易造成眩光和照度不均匀的问题,影响室内视觉舒适度,所以采用穿孔金属表皮在一定程度上可以避免眩光。在穿孔金属板组中,孔隙率对六个指标的影响较大,孔径仅对 UGR、DGI 有一定影响。同时也反映出,动态 UDI 结果与静态 DF 结果不同,UDI不仅能反映光照不足的情况,同时也能反映光照过量的情况,这也正说明 DF 等静态采光指标不能反映设计参数变化对室内光环境的影响,因此有必要采纳使用动态采光指标对穿孔金属板的参数设计进行判断。 为了更好地知道参数与各个指标间的关系,笔者将孔隙率、孔径、UDI、DF、sDA300/50%、均匀度、UGR、DGI数据导入到SPSS中进行分析。结果验证之前的分析,孔径对DF、UDI、sDA300/50%、均匀度的影响可以忽略,孔隙率对DF、UDI、sDA300/50%、均匀度的影响较大。以下分别对五个指标进行分析。 3.3.1 穿孔率、孔径与DF 由表6可以看出,孔隙率的标准化系数0.996明显大于孔径0.006,说明在两个变量间,孔隙率对DF的影响大于孔径。在SPSS中当设置自变量选入方式为逐步法时,自变量孔径没有达到入选标准而被剔除,更进一步说明孔隙率对DF的影响远远大于孔径,且孔径对DF的影响可以忽略。 表6 孔径、孔隙率与DF相关度分析Table 6 Correlation analysis of porosity/pore and DF 将自变量孔径排除后,单独对自变量穿孔率与DF进行回归分析。得出DF与穿孔率间有高度正相关(r=0.999),且呈线性关系,随着穿孔率越大DF越大。 图7 孔隙率与DF线性回归分析图Fig.7 Porosity and DF linear regression analysis diagram 举例说明,当孔径为77 mm时,孔隙率以步长为5%变化,DF会随着孔隙率的增大呈线性变化,随孔隙率的增大而增大。当保持孔隙率为5%,孔径以步长为10 mm变化,DF与孔径变化线性关系不明显(表7)。 表7 孔径77 mm、孔隙率5%与DF线性回归分析Table 7 Pore 77 mm /porosity 5% and DF linear regression analysis diagram 若以此推断可知,当没有金属表皮遮挡时,室内的采光系数最大。但显然与笔者试图研究的穿孔金属表皮参数设置对室内采光效果的影响相背离。 3.3.2 自变量穿孔率、孔径与因变量UDI 由表8可以看出,穿孔率的标准化系数明显大于孔径。 表8 孔径、孔隙率与UDI相关度分析Table 8 Correlation analysis of porosity /pore and UDI 单独对自变量穿孔率与UDI进行回归分析。得出UDI与穿孔率间有高拟合曲线关系,R2为0.862。根据拟合公式Y=22.892+591.332-1 394.151x2推测,当穿孔率为21.2%时,UDI取值达到最大值。如图8所示,UDI值在穿孔率为15%时达到最大,存在一定误差。但可以看出,并非随着孔隙率越大,UDI取值越大,UDI可以反映出较高室内照度对室内采光舒适度的影响,比DF更适合作为采光评价指标。 图8 穿孔率、孔径与UDI回归分析图Fig.8 Porosity /pore and UDI regression analysis diagram 3.3.3 自变量穿孔率、孔径与因变量sDA300/50% 单独对自变量穿孔率与sDA300/50%进行回归分析如图9所示。因IESNA规定sDA300/50%时,未给出上限[3],因此对其分析结果与DF近似,随着穿孔率越大,值越大。但可以通过50%出现的位置称为有效采光进深。这里有效采光进深的定义相比较于某 DF 数量值(如3%)所在进深位置更为合理,因为 DF 指标本身仅反映了较少的采光影响因素[7]。如图10所示,通过sDA300/50%来确定有效采光进深发现,随着空隙率的增大,有效进深逐渐加大,在20%孔隙率时,有效进深已大于教室进深的一半(3.85 m)。且当穿孔率为35%时,可能会出现窗边过亮的情况,因此应综合考虑其他相关指标。 图9 穿孔率与sDA300/50%线性回归分析图Fig.9 Porosity and sDA300/50% regression analysis diagram 图10 穿孔率与有效进深Fig.10 Porosity and effective depth 3.2.4 自变量穿孔率、孔径与因变量均匀度 由于模拟的教室采用的是侧面采光,因此会存在照度均匀度较差的情况。根据德国DIN标准和英国CIBSE指南,一般照明方案产生的均匀性应优于0.6或0.8。从图11自变量穿孔率与均匀度进行回归分析,得出均匀度与穿孔率间有中强相关(r2=0.452)。在穿孔率为10%时,均匀度最大为0.7左右。当穿孔率大于10%时,随着穿孔率越大,均匀度越大,因为明亮的光线集中在窗户附近,均匀度越低,室内的照度对比度越大,视觉舒适度越低,照度均匀度较差时,人的瞳孔会不断变换大小,易产生疲劳感,引起视觉功能下降,从而影响工作和学习[8]。 图11 穿孔率与均匀度回归分析Fig.11 Porosity and uniform regression analysis diagram 3.3.5 自变量穿孔率、孔径与因变量 UGR、DGI 由图12可以看出,UGR 与穿孔率呈高拟合曲线关系。据表5可知,UGR=22 时,刚刚不舒适,所以当穿孔率≤20%时,UGR≤22。而 DGI 与孔径呈高拟合曲线关系,当 DGI=22时,属于可接受,此时孔径为40~50 mm之间。综合来看,当穿孔率≤20%,孔径为40~50 mm之间时,室内受眩光的影响较小。 图12 穿孔率与UGR回归分析及孔径与DGI回归分析Fig.12 Porosity and UGR regression analysis diagram &Pore and UGR regression analysis diagram 文章通过以上对模拟数据的统计和分析发现,在教室外立面运用穿孔金属表皮有利于避免眩光,增大室内照度均匀度,提高视觉舒适度。同时还发现金属表皮的穿孔率是影响室内采光效果的主要因素。DF及sDA300/50%均随着孔隙率的增大而增大,在 20%孔隙率时,有效进深已大于教室进深的一半(3.985 m)。UDI 与孔隙率存在曲线关系,到达最大值 时,会随着孔隙率的增大而减小。这与我们判断的孔隙率的增大会带来室内靠窗局部过亮,反而 UDI 会减小的情况是吻合的。同时在此种模拟条件下,当孔隙率达到 15%时,室内采光效果 UDI 最佳。均匀度与孔隙率也存在曲线关系,在穿孔率为10%时,均匀度最大为0.7 左右。穿孔率为15%时,均匀度在0.5~0.6之间。孔径大小对眩光舒适度有一定影响,孔径为40~50 mm 之间时,室内受眩光的影响较小。 由此可见,在评价建筑的天然光环境时,使用动态的光环境指标代替传统的评价 DF 有其必要性。通过对比六个指标可以综合判断,穿孔率在 15%~20%时,孔径为40~50 mm之间时,此种条件下室内天然采光效果较好。本文采用的模型是标准教室室内单元,实际情况中可能会存在差异,目前分析得出的结论可以作为当前案例的天然光环境设计或者改善的参考。在实际情况中,若模型参数变化,可能会导致不同的结果。1 设计对象

2 研究方法
2.1 参数化模型建立及模拟分析
2.2 建模及参数设置




3 模拟结果与讨论

3.1 对比组与穿孔金属表皮组
3.2 穿孔金属表皮组之间对比
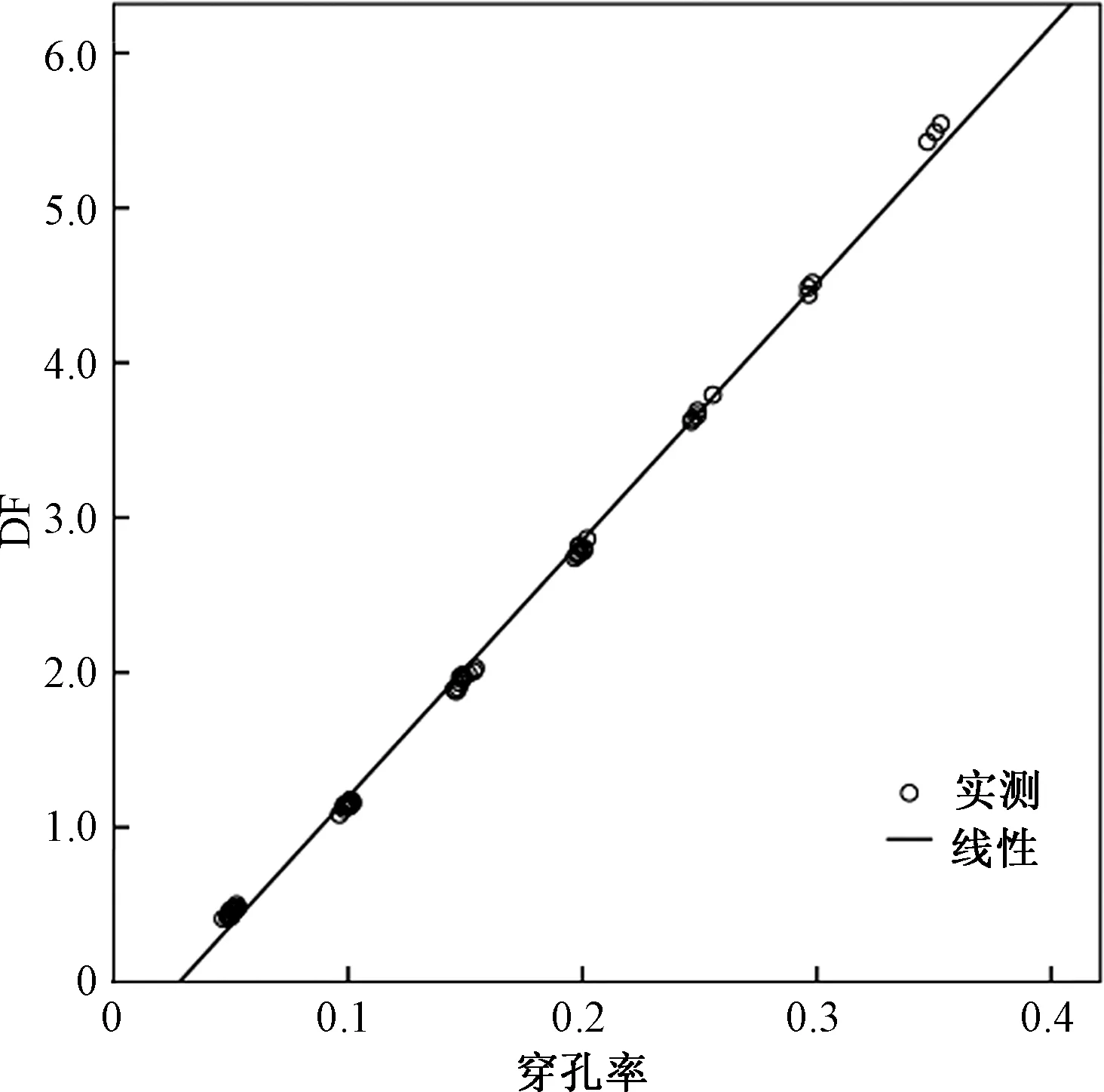
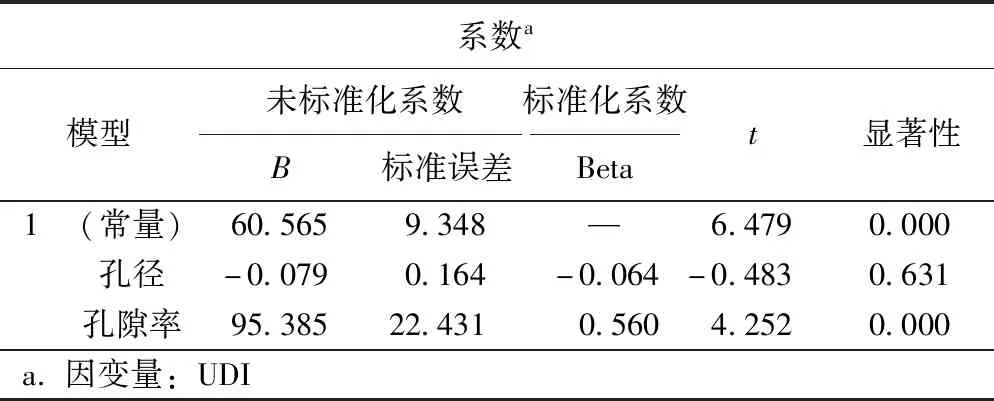
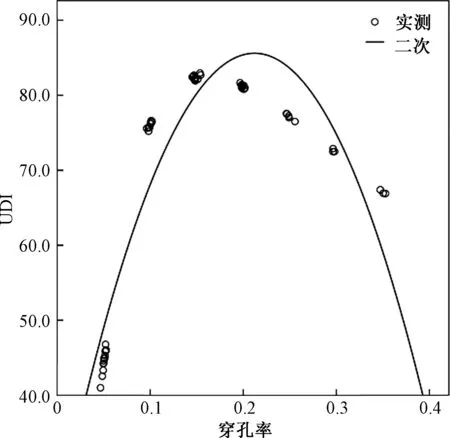
3.3 模拟数据回归分析





4 结论
