基于改进模糊C回归聚类的水轮发电机组的模糊辨识

罗红俊，马 龙，张官祥，魏春阳，陈绪鹏，金学铭，李超顺

（1.中国长江电力股份有限公司白鹤滩电厂，四川凉山615400；2.华中科技大学土木与水利工程学院，武汉430074；3.长江三峡能事达电气股份有限公司，武汉430000）

水轮发电机组具有时变、强非线性、非最小相位等特性，实现其精确建模一直是学术和工程应用研究的重点和难点，也是实现高品质控制的基础。

建立被控对象的数学模型的方法大致可分为机理建模和系统辨识两种方法。前者基于对系统特性和内部机理的清晰认知，后者是一种基于数据驱动的建模方法。由于水轮机内部的运动规律非常复杂，人们目前还无法给出水轮机的精确解析模型。而利用系统辨识方法可以建立能准确表达水轮发电机组的数学模型，克服解析法因机理不清或结构表述困难而难以准确建模的问题。

T-S 模糊模型是复杂系统辨识的有力工具，它结构简单并且能够以任意精度逼近非线性系统［1］。前提参数辨识和结论参数辨识是T-S 模糊模型辨识的两大部分，通常采用模糊聚类算法来进行前提部分辨识［2-7］。聚类算法将输入空间划分成若干子空间，每个子空间对应一个局部线性子模型。以模糊C 均值［8］为代表的基于点原型的聚类算法将输入数据空间划分成超球形，仅通过样本与中心之间的几何距离来定义聚类，并不能很好地保障子模型的线性度。为了克服这一局限，Hathaway 和Bezdek［9］对模糊C 均值进行了改进，得到模糊C 回归模型聚类算法。由此，发展了一系列基于超平面型聚类的T-S 模糊模型辨识方法［10-14］。

为了提升聚类效果，进一步提高模糊模型辨识精度，笔者对于模糊C 回归算法进行了改进。首先，笔者应用改进后的模糊C 回归算法进行前提部分辨识。初始化聚类超平面，通过最小化聚类目标函数求得聚类样本对于超平面的隶属度，并将得到的回归方程与系统实际输出之间的距离的倒数作为权值赋予各样本的隶属度，加权后的隶属度构成的对角矩阵作为加权最小二乘法的权重矩阵，用以更新聚类超平面。在迭代达到精度要求后，即得到最优聚类结果。然后，采用新提出的超平面型隶属度函数计算样本隶属于模糊规则的隶属度。最后，利用带遗忘因子的递推最小二乘法在线辨识结论参数。将所提出的模糊辨识方法用于辨识某水电厂的水轮机调速系统，实验结果验证了所得模型的高精度和强泛化能力。

1 T-S模糊模型

T-S模糊模型分为前提部分和结论部分，以第i条模糊规则为例，T-S模糊模型［1］的结构如下：

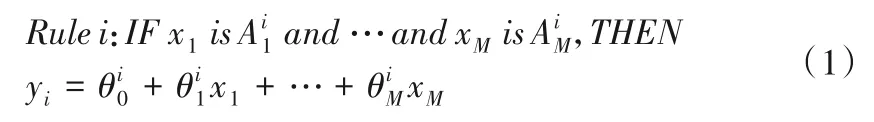
对于第k个输入向量，模型的最终输出以加权解模糊的形式表示：

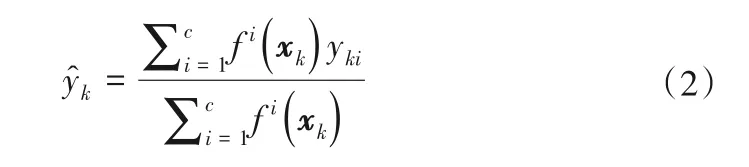
式中：f i(xk)为第k个输入向量对于第i条模糊规则的总隶属度。

2 T-S模糊模型辨识方法

2.1 前提部分辨识

模糊C回归聚类算法［9］中，第i类中的数据样本符合同一个线性回归模型：

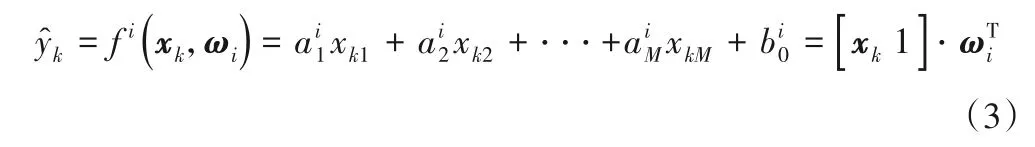
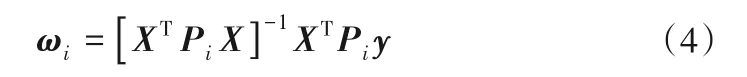
其中X=[xk1]n×(M+1)，y=[yk]n×1，以样本对于聚类超平面的隶属度构成的对角矩阵作为权重Pi。

2.2 基于改进模糊C回归聚类的前提参数辨识

模糊C回归算法的聚类目标函数为：

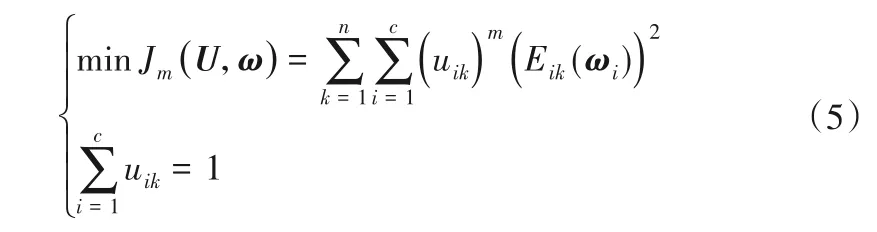
式中：U=[uik]c×n，m为模糊加权指数；Eik为系统输出与聚类超平面间的距离误差：

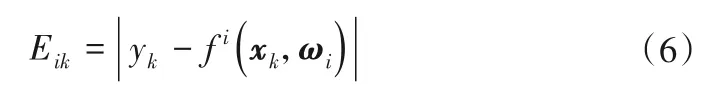
基于改进模糊C回归聚类的前提参数辨识方法的具体步骤如下：

（1）设置相关参数。构造输入输出数据对(xk，yk)，给定聚类数c，模糊加权指数m，迭代终止阈值ε以及最大迭代次数Tmax。

（2）计算最优聚类超平面。

①令t= 0，按照式（4）初始化聚类超平面，其中权重矩阵P的初值取为单位矩阵。

②依据式（6）计算误差值Eik。

③以（5）为目标函数，用拉格朗日乘子法求解聚类样本(xk，yk)隶属于超平面的隶属度：

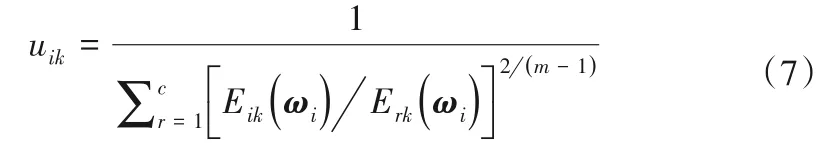
④对计算超平面所用的矩阵P进行改进。

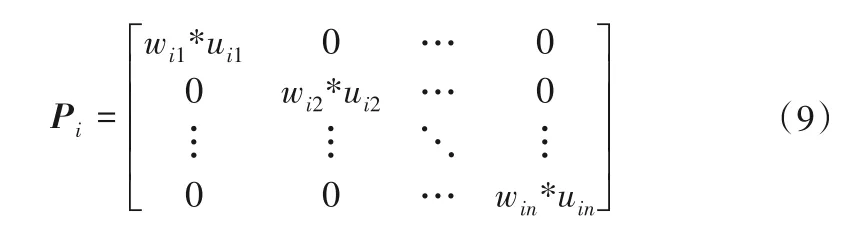
以误差值的倒数wik作为权值赋给相应的隶属度uik，由加权后的隶属度构成Pi进行接下来的迭代计算。

⑤利用式（4）更新聚类超平面。

⑥t=t+1，重复执行步骤②至⑥，直到或者t> Tmax。达到终止条件后，输出超平面参数向量ωi。

（3）利用新提出的超平面型隶属度函数计算各样本的隶属度。

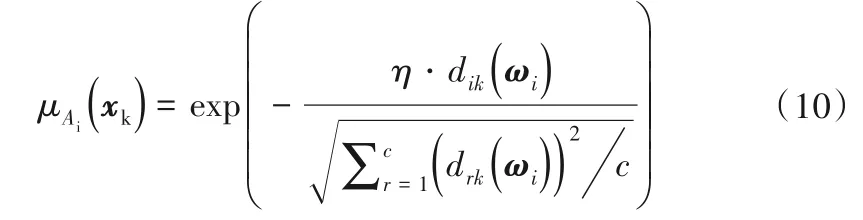
式中：η为调节系数；dik(ωi)表示第k个样本到第i个聚类超平面的距离，由下式定义：

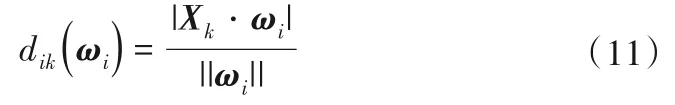
由于误差值Eik表示实际输出与聚类超平面之间的距离，它的值越小，样本(xk，yk)的权重越大，因此提出了误差值的倒数wik这一指标用于改进加权矩阵Pi。改进后的加权矩阵可以加快迭代计算的收敛速度，使得聚类超平面朝着更优的方向更快地更新。新提出的超平面型隶属度函数避免了将超平面转化为超球形聚类参数，不仅保留了超平面聚类在T-S 模糊模型辨识中的优势，而且减少了额外的计算量。

2.3 结论参数辨识

将n个输入输出数据对(xk，yk)(k= 1，2…n)整理成矩阵形式：

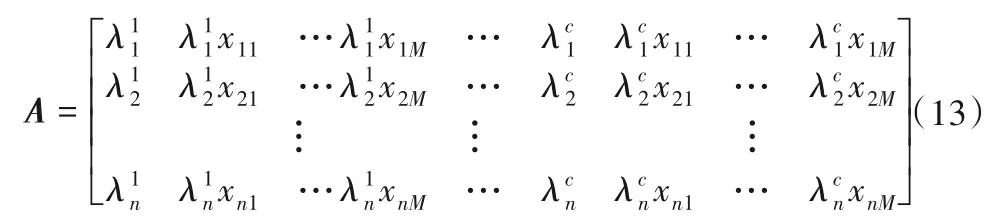
本文采用带遗忘因子的递推最小二乘法按照以下步骤来辨识式（12）中的结论参数。

①将系数矩阵A和系统输出y对应地划分为若干块，每一块包含若干个向量或仅包含一个向量。

②令k= 0，k代表待处理数据块的编号。按照式（15）初始化结论参数，并用式（16）初始化迭代参数P（0）。

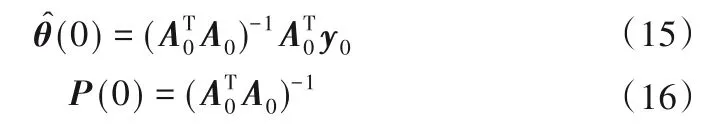
③k=k+ 1，计算相应的参数值：

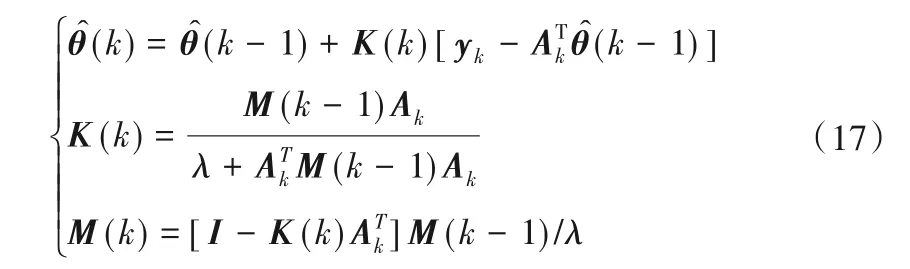
结论参数得到后，可计算出与输入数据块相应的输出估计值向量：

④重复步骤③直到所有的数据块处理完毕，那么就得到了最终的结论参数以及完整的预测输出序列。

带遗忘因子的递推最小二乘法赋予新的观测值更高的权重，并逐渐遗忘旧的样本，它的应用使得辨识得到的模型可以随着系统的变化实时地调整结论参数，这些是普通最小二乘法无法实现的。

3 水轮发电机组模型辨识

以混流式机组为例，水轮发电机组主要包含有压引水系统、水轮机和发电机三部分。水轮机采用全特性数学模型，引水系统采用时滞方程模型，发电机采用一阶惯性环节［15］。水轮发电机组结构如图1所示。

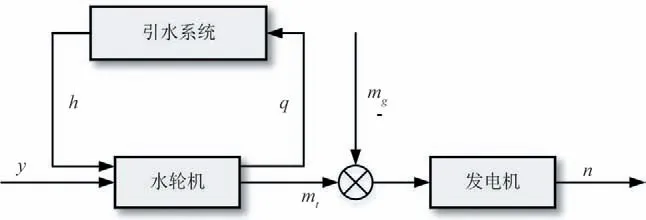
图1 水轮发电机组结构图Fig.1 Structure diagram of hydro-turbine generating unit

目前还无法建立精确的水轮机模型，因此实现水轮发电机组的高精度建模仿真比较困难。考虑到利用系统输入输出数据集进行系统辨识可以得到精确模型，我们采用基于改进模糊C 回归聚类的T-S 模糊模型辨识方法对水轮发电机组进行建模。

图2所示模型辨识图说明了水轮发电机组模型辨识的过程。将水轮发电机组视为一个整体，以其输入输出构建数据对样本，通过改进模糊C回归算法得到聚类超平面参数，然后利用新提出的超平面型隶属度函数计算各样本的隶属度，最后采用带遗忘因子的递推最小二乘法辨识结论参数。利用辨识所得模型参数，可计算模型输出，即转速估计值序列。

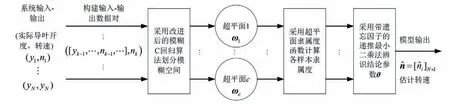
图2 水轮发电机组模型辨识图Fig.2 The identification diagram of hydro-turbine generating unit model

4 仿真实例

本节首先采用3 个常用的非线性对象作为实例，以验证所提辨识方法与其他方法相比具有更佳的性能。然后，将所提方法用于某水电站水轮发电机组的模糊辨识。

为了衡量辨识性能，我们采用均方差MSE作为性能指标：

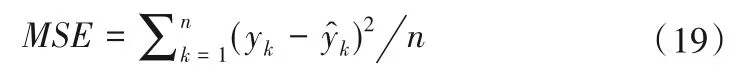
式中：yk和分别为第k个系统输出和模型输出。

4.1 一维Sinc函数建模

一维Sinc 函数是先前文献［16］提出的用于测试建模精度的示例，定义如下：

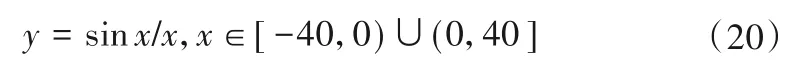
从[-40，0) ∪(0，40]中均匀采样121 个输入数据点，并产生对应的输出数据，用这121 个输入输出数据对进行建模。对数据集进行划分，用于初始化的数据块大小为52，约占训练集数据总数的40%，其余的数据块大小设置为1。取模糊指数为m= 2，模糊规则数为c= 4，取遗忘因子为λ= 0.95；根据试错法，确定调节系数为η= 4.8。将结果与基于模糊C 均值算法的辨识方法以及基于模糊C回归聚类转化为超球形隶属度的辨识方法进行比较。图3展示了应用本文所提方法得到的模型辨识结果，与其他方法的精度对比在表1 中给出。表中，传统方法1指基于模糊C 均值算法的辨识方法，传统方法2 指基于模糊C回归聚类和高斯超球形隶属度的辨识方法。表1结果表明本文辨识方法比其他两种方法具有更高的建模精度。

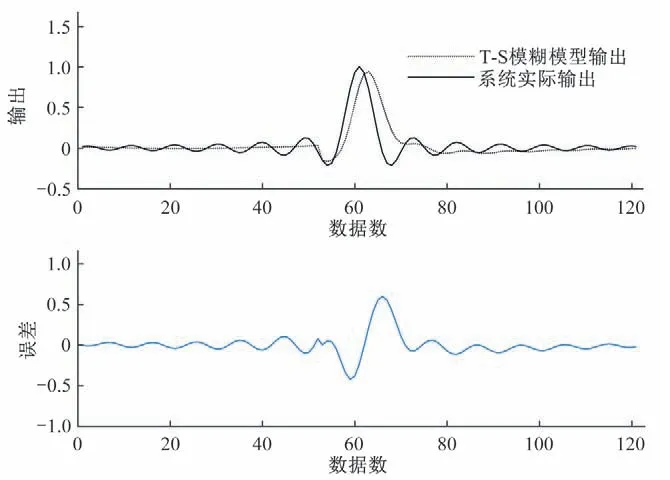
图3 本文方法对于一维正弦函数的辨识结果Fig.3 The identification result of our approach for the one-dimensional Sinc function

表1 3种方法对于一维正弦函数辨识精度比较Tab.1 Comparison of the identification accuracy of three methods for the one-dimensional Sinc function

4.2 非线性差分方程建模

选用如下二阶非线性差分方程进行模糊建模，这个例子摘自Sugeno等人的研究［17］。

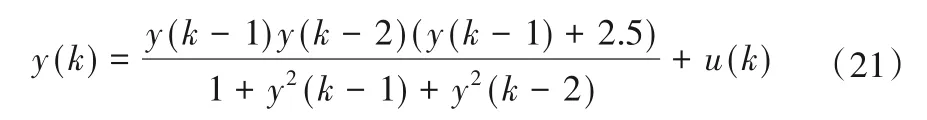
首先，输入500 个[-2，2]上均匀随机分布的输入信号u(k)，产生500 个训练样本用以建立T-S 模糊模型。用于初始化的数据块大小为200，其余的数据块大小设置为1，取m= 2，c= 4，λ= 0.95，η= 4.6。其次，输入一个正弦信号u(k) =sin(2k/25)产生500个测试样本用来测试辨识所得模型的性能，测试数据块的大小取为1。图4 显示了采用本文所提方法对该非线性方程进行建模和测试的结果，与其他方法的对比在表2列出。表2 说明本文所提方法不仅具有更高的辨识精度，还具有更强的泛化能力。同时，以这一示例为例，给出最终模型对应的相关参数。

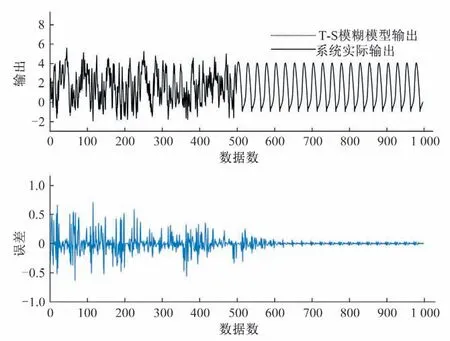
图4 本文方法对于非线性差分方程的辨识结果Fig.4 The identification result of our approach for the nonlinear difference function

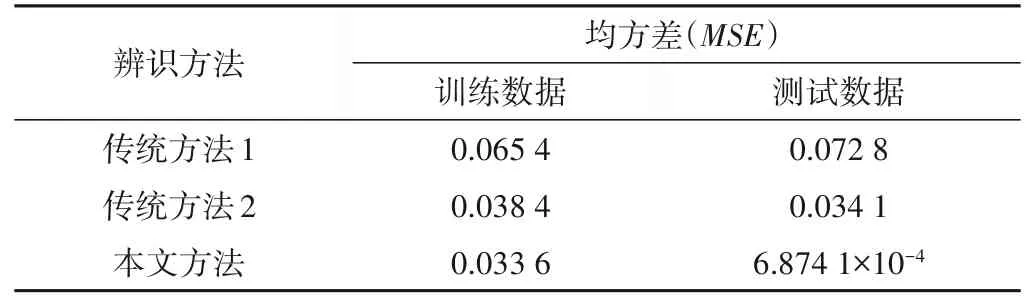
表2 3种方法对于非线性差分方程辨识精度比较Tab.2 Comparison of the identification accuracy of three methods for the nonlinear difference function

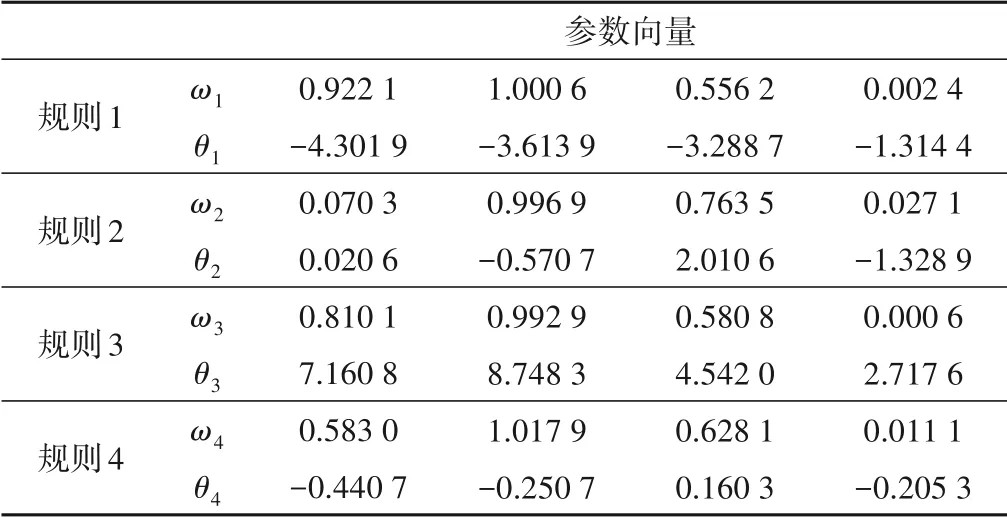
表3 对于非线性差分方程所建模型的参数列表Tab.3 List of parameters of the model built for the nonlinear difference function

4.3 Mackey-Glass混沌系统建模

Mackey-Glass 混沌微分时延方程是用于比较不同模型学习及泛化能力的有力工具，Mackey-Glass 混沌时间序列由式（22）生成：

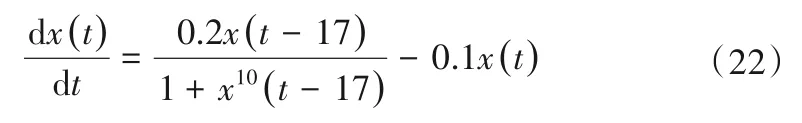
为实现更高的预测精度，使用x（t-18），x（t-12），x（t-6）和x（t）这4 个过去的值，来预测值x（t+6）的序列。在本文中，从Mackey-Glass 混沌时间序列中选取1 000 个输入-输出数据对［x（1 001），…，x（2 000）］作为数据集，其中前500 个数据对［即x（1 001），…，x（1 500）］用作训练集；剩余的500 个数据对［即x（1 501），…，x（2 000）］用作测试集。取m= 2，c= 10，λ= 0.95，η= 5.3。建模阶段用于初始化的数据块大小为191，其余的数据块大小设置为1。

图5展示了采用本文辨识方法对Mackey-Glass混沌时间序列进行建模和测试的结果，与其他方法的对比记录在表4 中。从表4可以看出，辨识所得的模型精度高，泛化能力强。

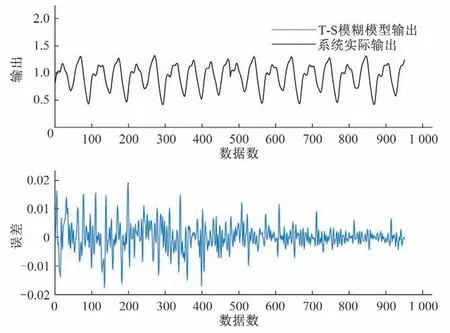
图5 本文方法对于Mackey-Glass混沌时间序列的辨识结果Fig.5 The identification result of our approach for the Mackey-Glass chaotic time series

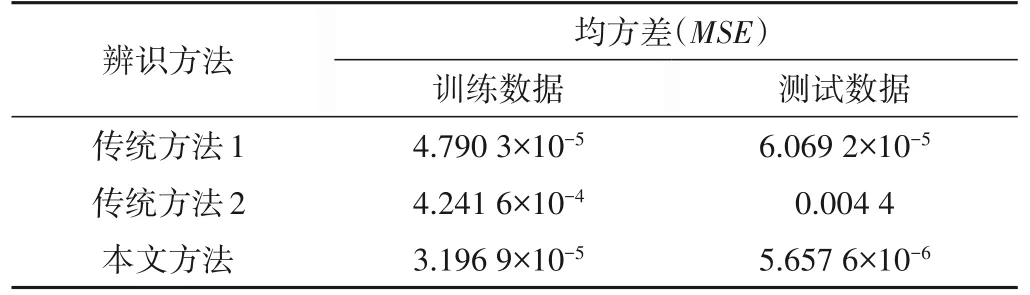
表4 3种方法对于Mackey-Glass序列辨识精度比较Tab.4 The parameter vectors of the model built for the nonlinear difference equation

为了证明本文所提的改进聚类算法比模糊C回归聚类算法具有更快的收敛速度，将3 个示例下两种聚类算法的运行时间记录在表5。

从表5 可以看出，改进后的超平面聚类算法具有更高的聚类效率，可以更快得到最优聚类超平面。再结合辨识结果可知，精度和速率都得到了提升。

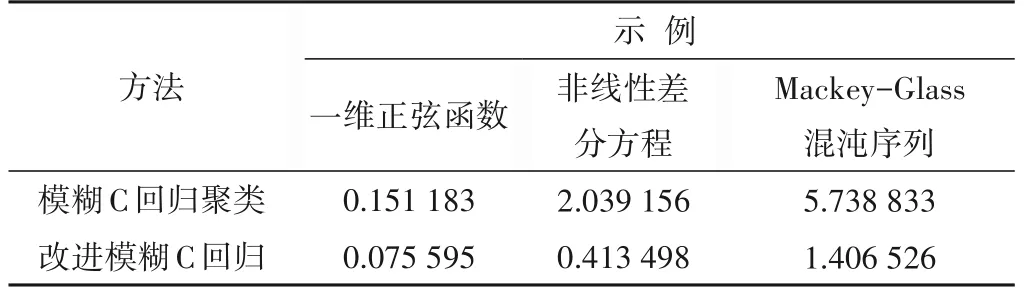
表5 3个示例下两种聚类算法耗时Tab.5 The time-consuming of two clustering algorithms under three examples

4.4 水轮发电机组模糊模型辨识

依据某水电站水轮发电机组的输入输出采样数据，可以建立水轮发电机组的T-S模糊模型。本文考虑水轮发电机组的输入输出序列分别为导叶开度u(t)和转速y(t)，基于系统的输入输出采样值构造模型的输入输出数据对[xk，yk]，其中xk=[u(k- 1)，u(k- 2)，y(k- 1)，y(k- 2)，y(k- 3)]是由历史开度和转速组成的维数为M= 5的模型输入向量，yk为第k个时刻的转速y(k)。选取同一种水头下的双机开机、同时甩负荷、同时减3%负荷、同时减8%负荷4 种情况下1 号机组的数据作为训练集进行建模，在另一种水头下分别测试辨识所得模型在各种工作状态下的精度。取m= 2，c= 2，λ= 0.95，η= 5.6。训练阶段，输入的是输入输出数据对的随机序列，用于初始化的数据块大小为训练集数据总数的40%，其他数据块大小为10。训练所得的模型精度可达7.475 7×10-14，辨识结果如图6所示。

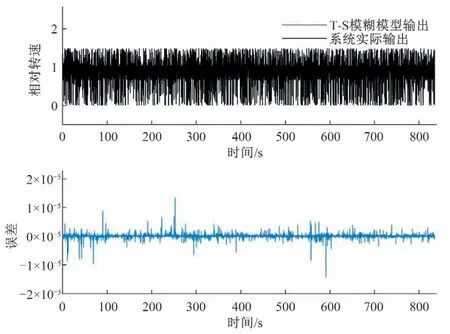
图6 本文方法对于该水轮发电机组的辨识结果Fig.6 The identification result of our approach for the hydro-turbine generating unit

在测试阶段，用辨识得到的模型对于另一水头下甩负荷，双机开机，减3%负荷以及减8%负荷4 种情况依次进行测试，数据块的大小依次取为10，25，35，50。以双机开机为例给出测试结果，如图7所示。

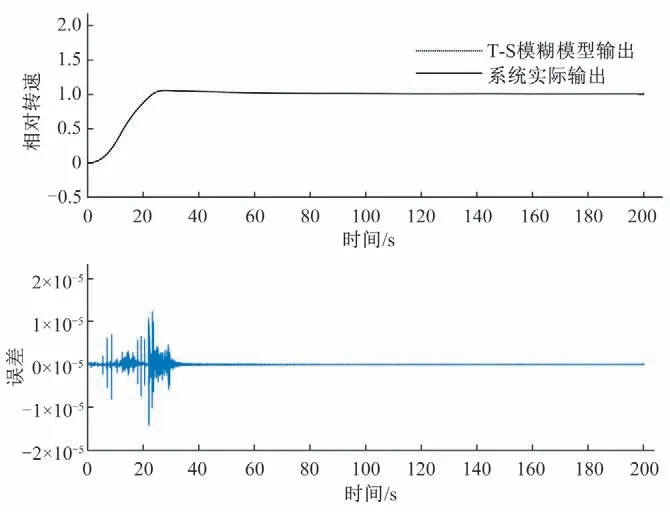
图7 辨识所得模型对于双机开机的测试结果Fig.7 Testing results of the identified model for dual machine startup

具体的训练和测试性能指标列在表6中。结果表明本文提出的方法比传统方法具有更高的建模精度，并且辨识得到的模型对于不同的测试集均具有很好的辨识结果，总体优于传统方法。由此可见，本文的T-S 模糊模型辨识方法在进行水轮发电机组辨识时具有很高的精度和相当强的泛化能力。

5 结论

本文提出了一种基于改进模糊C回归聚类算法的T-S模糊模型辨识方法用于水轮发电机组的精确建模，依据实际的输入输出数据建立与待辨识机组匹配的T-S模糊模型。用改进的模糊C回归聚类算法划分模糊空间，提升了聚类效果；采用新提出的超平面型隶属度函数得到前提参数，避免了转换为超球形聚类参数带来的优势削减和额外的计算量；再用带遗忘因子的递推最小二乘法辨识结论参数，进一步提高了辨识精度。三个数学示例和一个水轮发电机组实例的模型辨识结果及与其他方法的对比结果表明，本文所提的模糊辨识方法具有较高的建模精度和较强的泛化能力。□