输水明渠壅水状态断面流速特性三维仿真研究

2021-09-28王静茹管光华靳伟荣

中国农村水利水电 2021年9期

王静茹，管光华，靳伟荣，熊骥

（1.武汉大学水资源与水电工程科学国家重点实验室，武汉430072；2.湖北省国际灌排研究培训中心，武汉430072）

0 引言

灌区量测水设施是实施计划用水、合理配水的重要手段；是农业用水计量收费的重要依据和保证；也是水资源管理三条红线的重要技术支撑，是建设现代化灌区重要的一环。传统的量水方法有堰槽测流、流速仪测流、超声波测流、水工建筑物测流等。由于我国灌区量水的需求与日俱增，近些年来涌现了大量的新型量水技术和方法，如雷达波流速仪测流、多点超声波测流等。

目前在实际工程中使用标准断面进行量水，常忽略了渠道壅水高度对于水位流量关系的影响，即认为标准断面的水位-流量是固定的［1，2］。而使用雷达技术测流只能得到渠道水面流速，要得到断面平均流速还需乘以一定的水面流速系数，因此水面流速系数的取值对于这一类流速仪的精度具有决定性的作用。因此，本文主要研究明渠在不同下游壅水高度条件下水位-流量关系和水面流速系数的变化规律，结合我国灌区内渠道主要断面形式，本文选取的渠段均为具有梯形断面的缓坡明渠。

自然界中大多数的明渠水流都是紊流，对于明渠紊流的运动规律和水力特性许多学者进行了一定的探索和研究。Keu⁃lengan［3］将平板边界层的研究与明渠水流相结合，提出明渠断面垂线上沿渠道方向的流速满足对数分布。后来有学者［4］认为明渠水流可沿水深分成内区和外区。内区由黏性底层、过渡层和对数区组成，外区用Coles［5］提出的尾流函数对对数流速分布进行修正。Prandtl 等［6］和Afzal［7］给出了指数形式的流速公式，认为主流区的流速梯度和水分子的黏性呈渐进指数关系。由一些学者的研究成果［8-10］知，矩形断面和梯形断面顺水流方向流速-u分布如图1所示，最大流速发生在水面以下；矩形明渠过水断面上水平流速-v和垂直流速-w分布图如图2所示，可以看出有表面涡流和底部涡流，即有二次流的存在。

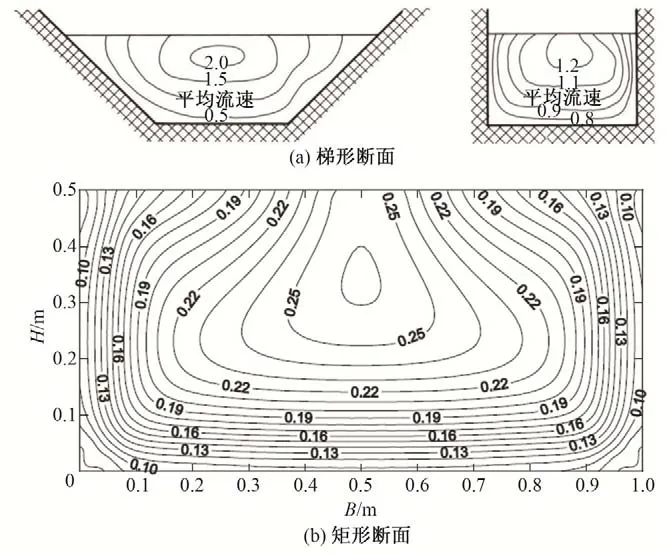
图1 典型断面顺水流方向流速分布图Fig.1 Velocity distribution diagram of typical cross-section along the flow direction

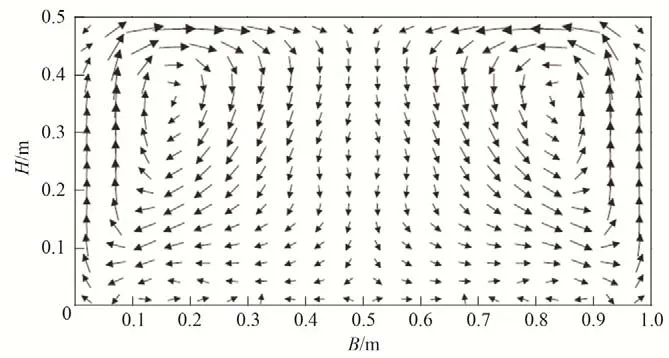
图2 矩形明渠和分布图（二次流）Fig.2 Velocity distribution diagram at horizontal direction and vertical direction

现有的明渠流速分布规律是针对恒定均匀流的，但实际渠道中糙率的不均匀分布，泥沙淤积，下游壅水等都会影响渠道中的流速分布。由于输配水渠道系统中常用节制闸进行水位、流量调节，渠道在临近节制闸处会产生不同程度的壅水，尤其是在渠道高水位低流量运行时。目前少有文献研究下游壅水高度对过水断面的流速分布的影响，因此本文选取漳河三干渠三分干，基于FLOW-3D 三维仿真，对输水明渠在下游壅水时的断面流速分布进行研究。

1 数学模型

1.1 控制方程

FLOW-3D中采用的控制方程为N-S方程，并且在求解N-S方程时采用雷诺平均法，在控制方程中分别加入面积分数和体积分数［11］。

其连续性方程为：

动量方程为：

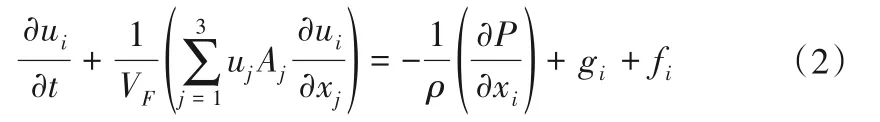
式中：i、j=1、2、3；ui为x、y、z方向的速度；Ax、Ay、Az为计算单元x、y、z方向面积；VF为各计算单元内液体的体积分数；ρ为液体密度；P为压强；gi为重力；fi为雷诺应力［12，13］。

1.2 湍流模型

RNGk-ε模型是基于重整化群（Renormalization Group）的理论提出来的标准模型的修正方程。RNGk-ε模型相对于k-ε模型，可以更好地处理高应变率及流线弯曲程度较大的流动［14-16］。因此本文采用RNGk-ε模型。RNGk-ε模型的湍动能k和湍动能耗散率ε方程分别为：

湍动能方程：

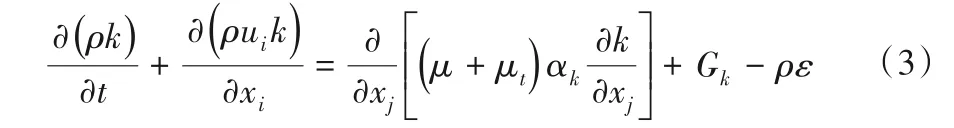
湍动能耗散率方程：

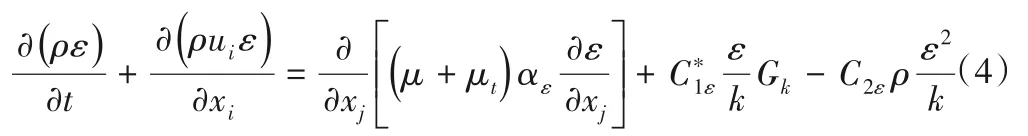
式中：k为湍动能，m2/s2；ε为湍动能耗散率，kg·m2/s2；μ为流体动力黏滞系数，N·s/m2；μt为流体的湍动黏度，μt=ρCμk2/ε，N·s/m2；αε，αk，C1ε和C2ε为经验常数，βη3），其中=0.012，C1ε=1.42；常数C2ε=1.68；Gk为由平均速度梯度引起的紊动能产生项，可由式定义［14，17］。

1.3 自由表面

在数值模拟中，自由表面就是气体和液体的交界面，气体只对液体施加压力。FLOW-3D采用truVOF方法追踪自由表面流动。在水气两相流中，定义函数αw和αa分别为计算单元中水和气的体积分数。每个单元中，水和气的体积分数之和为1，即αw+αa=1。当αw=0 时，计算单元内全为气相；当αw=1 时，计算单元内全为液相；当0<αw<1 时，计算单元内部分是水，部分是气，包含自由表面［18］。

2 三维流场建模

漳河灌区三干渠三分干全长36.8 km，本次建模主要选择从三干渠三分干分水闸到下游三分干卞庙节制闸的一段，全长9 300 m。该渠段的几何参数及水力特性为：底坡i=1/8 000，底宽b=4 m，边坡系数m=1.75，糙率n=0.015，渠道设计流量10 m3/s，渠道加大流量为13 m3/s。

2.1 模型范围及网格划分

2.1.1 模型范围

模型范围取其中的100 m，按原型1∶1建立几何实体模型。

2.1.2 网格无关性检验

网格质量的好坏直接影响到数值计算的稳定性和精度。选择合适的网格数目对于数值计算的准确性以及缩短计算时间有非常重要的影响［19-21］。本文取10 m 长渠道，对0.2，0.1，0.05，0.03 m 四种网格宽度的均匀网格进行无关性检验。网格形状为正方体。数值模拟结果如表1所示。不同网格宽度稳定后沿程水深如图3所示。

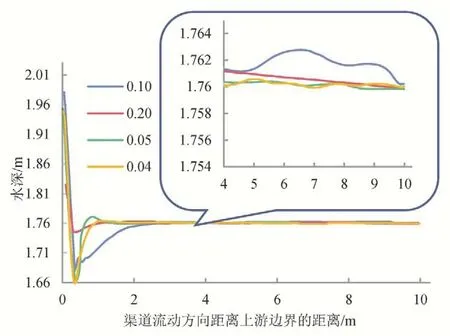
图3 不同网格宽度稳定后沿程水深Fig.3 The steady water depth under different mesh sizes

由表1可知：当网格尺寸大于0.05 m时，网格宽度对模拟结果影响较大，此时网格尺寸越小，模拟结果越接近于恒定均匀流，但相应运行时间会大幅增加；当网格尺寸小于0.05 m 时，网格宽度对模拟结果影响较小。因此出于时间和精确度的考虑，本文网格宽度取0.05 m。

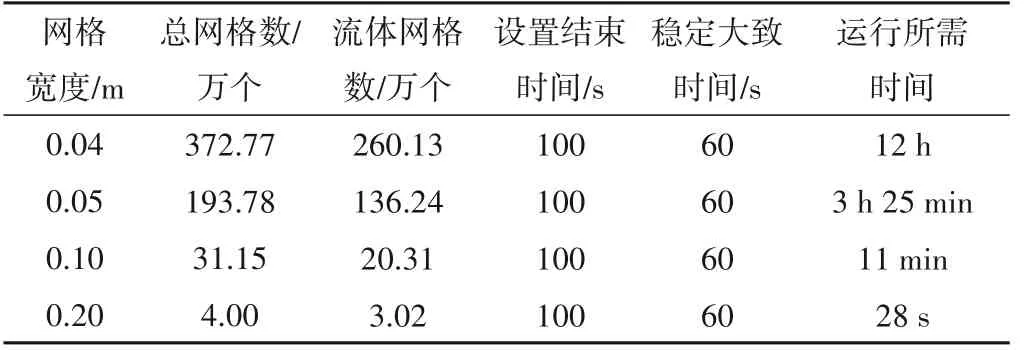
表1 10 m长渠道不同网格宽度模拟结果Tab.1 Simulation results of a 10 m long channel under different mesh sizes

2.1.3 网格划分

当模型渠道长度为100 m，网格宽度为0.05 m 时，总网格数可达到千万以上，因此考虑用相连网格块，在加密网格的同时尽可能减少成指数倍增长的网格数。且模拟结果表明，从水面到渠底依次用0.05、0.1、0.2 m 的网格宽度与计算区域均用0.05 m的网格宽度沿程水深及流速分布大致相同。

因此计算区域用3 个连接的网格块来划分，靠近渠底的网格块单元尺寸为0.2 m×0.2 m×0.2 m，渠道中部网格块单元尺寸为0.1 m×0.1 m×0.1 m，靠近水面处网格块尺寸为0.05 m×0.05 m×0.05 m，网格总数为500～600万，具体划分见图4。

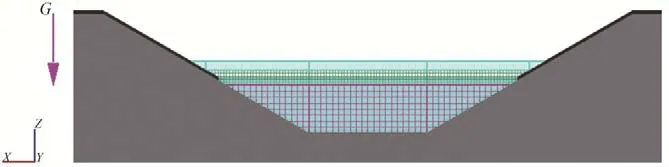
图4 网格划分示意图Fig.4 Sketch of mesh discretization

2.2 物理模型、边界条件、初始条件

除了紊流模型选择RNGk-ε模型外，还需要在软件中选择重力模型和黏性流动。重力模型中设定重力加速度为9.8 m/s2。

上游边界条件为固定流量边界条件（不设定流体高度，默认流体从整个边界开放区域流入，流动方向与边界垂直）；下游边界为固定水位的压力出流边界条件，水深hd=h0+Δh，其中h0是正常水深1.76 m，Δh为壅水高度，分别取0、10、20、30、40、50 cm；渠道两侧及底部为无滑移的wall边界条件；上部为压力为0的压力边界条件。

本文选取沿程1.76 m 的正常水深作为初始条件，用CAD 建立水深模型，输出为stl格式，再将其作为流体导入。

2.3 单位、流体特性及时间设置

选择SI 单位制，流体为20 ℃的水。初始时间步长设置为0.001 s，最小时间步长设置为10-7s。时间步长的控制方法使用Stability and convergence 和stability，步长会自适应调节。

2.4 模型验证

下游壅水高度Δh=0 时，模拟的是恒定均匀流，数值模拟的结果与用HEC-RAS 计算和曼宁公式计算的沿程水面线对比如图5所示。由于上游边界条件的影响，用FLOW-3D 模拟出来的沿程水深在进口处会有0.2 m 的降落，很快稳定在正常水深1.76 m 附近，HEC-RAS 和曼宁公式计算出沿程水深均为1.76 m。FLOW-3D 得到的水面线误差小于1 mm，因此FLOW-3D 数值计算的结果具有一定可信度。

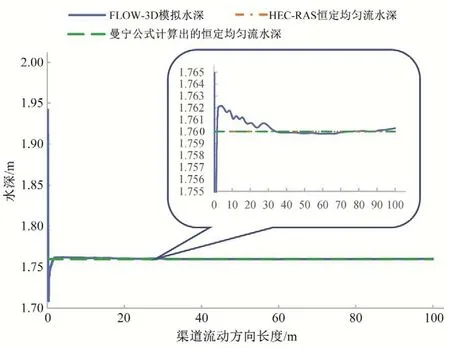
图5 数值模拟水深和HEC-RAS恒定均匀流水深Fig.5 Simulation results of water depth by flow3d and HEC-RAS

3 仿真及结果分析

3.1 渠道流速分布

国内外学者根据梯形断面渠道、矩形断面渠道、复式断面河槽等的室内试验和现场资料证实，渠道中心自由水面处的流速不是最大值，最大流速发生在自由水面以下。一些学者提出是由于过水断面存在二次流［22］。

图6（a）～（f）为距离上下游边界均50 m 的断面沿水流方向（y方向）的流速分布图。本文同样得到最大流速发生在自由水面以下。同时对过水断面流速等值线图分析可得：①渠道中垂线两侧流速分布大致对称相等；②在流量相同，下游水深不同的情况下，随着下游水深增大，即壅水程度的增大，最大流速点的位置相对水面向下降，且最大流速值减小；③渠道边壁处流速等值线图除靠近水面处向渠道中心弯曲外，其他地方近似与边壁轮廓平行。

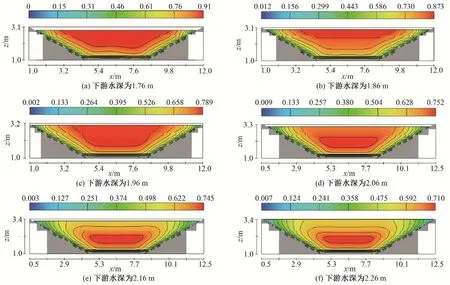
图6 距离上下游边界均50 m的断面沿水流方向（y方向）的流速分布图Fig.6 Distribution of velocity along y-axis at the cross-section 50 m away from upstream and downstream end

图7（a）～（f）为距离上下游边界均50 m 的断面沿水平方向（x方向）的流速分布图。结果表明：①边壁附近的水流有向中心聚集的趋势；②渠道中垂线两侧流速分布大致对称相等，且渠道中垂线附近流速大致为零；③在流量相同，下游水深不同的情况下，随着下游水深增大，即壅水程度的增大，此断面上水平方向流速最大值点的位置相对水面向下降，且最大流速值减小。

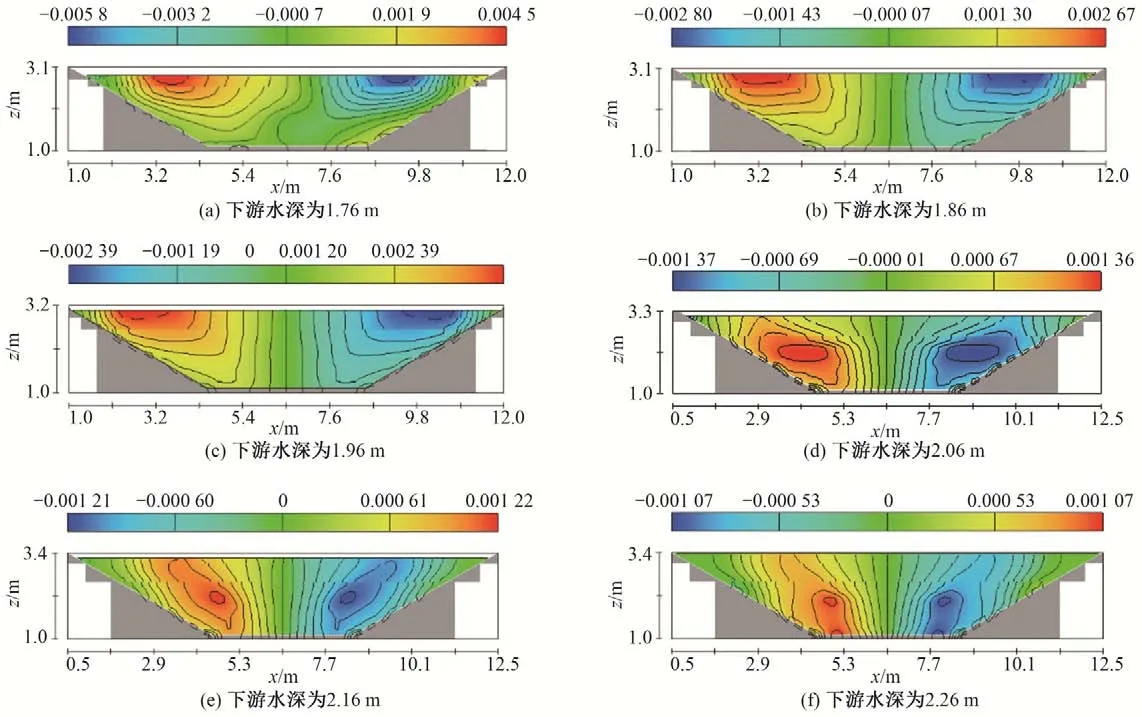
图7 距离上下游边界均50 m的断面沿水平方向（x方向）的流速分布图Fig.7 Distribution of velocity along x-axis at the cross-section 50 m away from upstream and downstream end

这可以用二次流来解释，由于边壁和自由水面的影响，在水面附近存在一个指向中心的二次流，将边壁附近的低速水流带到中心，这也是造成表面流速降低的原因之一［22］。

3.2 点流速测流的精度分析

使用雷达技术测流时，需要将雷达测得的表面点流速乘以水面流速系数k得到断面平均流速，然后根据过水断面面积得到流量：

式中：vc表示断面平均流速；vs表示水面平均流速。

通常情况下，在使用雷达测流之前会通过率定的方式确定一个固定的水面流速系数，设为k0。但渠道在实际运行过程中，由于受到壅水作用的影响，在流量不变的情况下，随着下游水深变化，水面流速系数和断面流速分布均会发生变化。

以本文所取漳河典型渠段为例，由于其底坡较小，因此下游边界水深改变导致的壅水影响范围较大。为研究相同流量下，下游水深不同时，相同断面处的流速分布和水面流速系数变化规律，取渠段内距上下游边界均50 m 的断面，研究不同下游壅水条件下采用不壅水时的水面流速系数k0测流导致的流量误差。

表2 中h表示断面处水深，A表示过水面段面积，Q1表示实际流量，由于仿真中设置入口处为固定流量10m3/s 并且水流为恒定流，因此各断面处流量均为10 m3/s，Q2表示根据k0计算得到的流量：

表2 Δh不同时使用固定的k0产生的测流误差Tab.2 Discharge measurement error using constant k0 under different values of Δh

由表2 可知，由于渠道底坡较小，下游水深边界改变，此断面水深几乎与下游边界相等，只小于下游水深1～5 mm，且相较于下游水深的减小值随下游水深的增大而增大。在该渠段内，如果忽略壅水作用对水面流速系数的影响，而采用固定的水面流速系数，所测量得到的流量误差随壅水高度的增加而增大，在壅水高度达到40 cm 时误差大于10%，不满足量水精度的要求。

3.3 水面流速系数

3.3.1 水面流速系数变化规律

本文对不同下游边界条件恒定非均匀流时离上游边界40、50、60、70 m 断面的水面流速系数进行了研究，如图8所示。为减小误差，每个水面平均流速的值均是选取稳定后3 个时刻数据的平均值。由图8 可知，下游水深条件改变时渠道沿水流方向各断面水面流速系数并不为一定值。下游水深变化量Δh=0、10、20 cm 时沿水流方向各断面的水面流速系数沿程略有增加，大致为1；Δh=30 cm 时沿程水面流速系数基本不变，为1.05；Δh=40 cm 或50 cm 时沿程水面流速系数从1.2～1.21 变小到1.1～1.12。

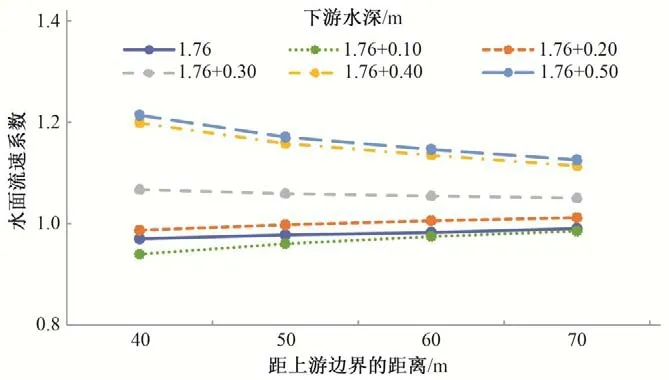
图8 距上游边界不同距离的断面的水面流速系数Fig.8 The values of surface velocity coefficient at different cross-sections

考虑到实际渠道运行过程中，下游水深边界改变，离上游边界距离的不同，最直接影响的物理量是水深。如图9所示，水深不变或增加10、20 cm 时，离上游边界40、50、60、70 m 的断面处水面流速系数基本维持在1附近，之后水深再增加时，水面流速系数也增大，水深从1.96 m 增大到2.16 m 时，水面流速系数增大地较快，水深从2.16 m再增大时，水面流速系数基本不变。

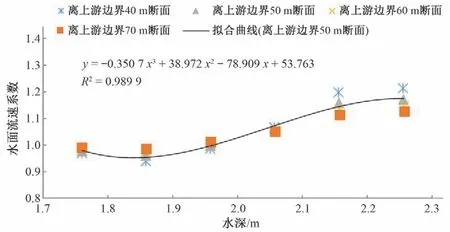
图9 各个断面上水面流速系数与水深之间的关系Fig.9 The relation between water depth and surface velocity coefficient at different cross-sections

因此在渠道实际运行过程中，Δh在20 cm 范围内时，用正常水深情况下率定的水面流速系数测流比较可靠，Δh大于20 cm 时，实际水面流速系数大于率定的水面流速系数，测量的流量会小于实测流量，造成一定的流量偏差。

3.3.2 考虑水深变化对水面流速系数进行修正

本文选取三次多项式对距上游边界50 m 断面处的水面流速系数和下游边界处的水深关系进行拟合，得到修正后水面流速系数k'与下游水深hd的表达式：

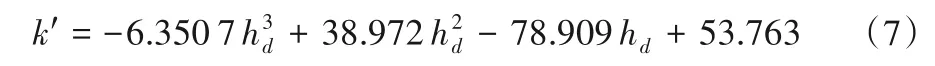
拟合曲线与三维仿真结果的决定系数R2=0.99，故可采用该式计算不同下游水深下该断面的水面流速系数，进而求断面流量。

由表3 可见，在本文所采用的工况下，k'值所推算出来的断面流量与实际流量误差小于1.4%。

表3 Δh不同时同一断面的水面平均流速和流量Tab.3 The average surface velocity and flow rate at the same section under different Δh

表3 中h表示断面处水深，A表示过水面段面积，Q1表示实际流量，由于仿真中设置入口处为固定流量10 m3/s并且水流为恒定流，因此各断面处流量均为10 m3/s，表示根据k'计算得到的流量：

3.3.3 多点流速测量

雷达测流采用的是无线电多普勒效应。得到的水面数据的个数与水面波浪和漂浮物有关。因此灌区实际测流并不能像数值模拟一样得到水面很多点的数据，只能测出水面有限点的流速。

本文对测点的个数与测流误差之间的关系进行了一定的讨论。测量水面上三点（离水面中心点距离0 m、±2m）、五点（离水面中心点距离0 m、±2 m、±4 m）、七点（离水面中心点距离0 m、±1.5 m、±3 m、±4.5 m）的流速得到的水面平均流速分别为v3、v5、v7，则测流产生的误差如表4所示。

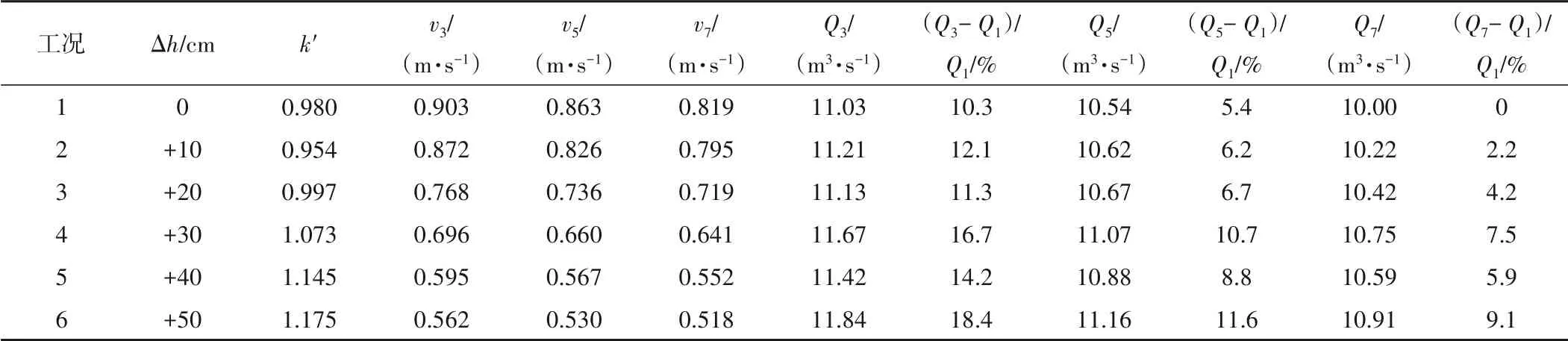
表4 多点流速测流产生的误差Tab.4 Discharge measurement error using multiple point measurement

表中Q3，Q5，Q7为根据v3、v5、v7和k'计算得到的流量，以Q3为例：

由表4 可知，水面测量的点流速越多，测流产生的误差越小。只测量水面3 个点的流速时，在6 种工况下产生的误差约在10%～19%范围内；五点流速的测流误差在5%～12%范围内；七点流速的测流误差在0%～9%范围内。因此测量表面流速的个数为7个时，测流误差可以接受，且壅水高度Δh<20 cm 时，测流误差在5%以内，误差相对较小。