常见地下水水质评价方法在日照市傅疃河下游地区的应用

2021-09-27袁杰杨鹏魏同政康日斐丁伟

安徽农业科学 2021年18期

袁杰杨鹏魏同政康日斐丁伟

摘要以日照市傅疃河下游地区多年地下水监测水质资料为基础，选取了17个监测点的溶解性总固体、总硬度、硝酸根、亚硝酸根等共17个指标作为水质评价因子，在评价过程中分别采用单因子评价法、传统及改进的内梅罗指数法、模糊数学法和改进的模糊数学法进行水质评价，并对这几种方法的计算过程、计算结果进行了对比。结果表明：这几种常用的评价方法均适用于地下水水质评价，但各有优劣。单因子评价法计算过程最为简单，根据评价结果可确定对水质影响较大的污染物，可分析出水環境质量的大体情况。内梅罗指数法考虑了污染最严重的因子和均值，改进的内梅罗指数法适用于了解水质的整个污染情况。模糊数学法通过权重和隶属度计算进行水质评价，体现了其非线性关系。改进的模糊数学法计算过程最为复杂，根据其评价结果可确定水质指数。结合研究区污染情况，可确定模糊数学法评价结果更贴合实际情况。

关键词傅疃河下游地区;地下水水质评价;单因子评价法;模糊综合评价;内梅罗指数法

中图分类号 X 824 文献标识码 A 文章编号 0517-6611（2021）18-0195-05

doi：10.3969/j.issn.0517-6611.2021.18.048

开放科学（资源服务）标识码（OSID）：

Application of Common Groundwater Quality Evaluation Methods in the Lower Reaches of Futuan River in Rizhao City

YUAN Jie，YANG Peng，WEI Tong-zheng et al （The Eighth Institute of Geology and Mineral Exploration of Shandong Province，Rizhao，Shandong 276826）

Abstract Based on the monitoring data of groundwater quality in the lower reaches of Futuan River in Rizhao City for many years， a total of 17 indices including total dissolved solids， total hardness， nitrate and nitrite were selected as water quality evaluation factors. In the evaluation process，single factor evaluation method， traditional and improved Nemerow index method， fuzzy mathematics method and improved fuzzy mathematics method were used for water quality evaluation respectively. The calculation process and calculation results of several methods were compared. The research results showed that several commonly used evaluation methods were suitable for groundwater quality evaluation， but each method had its advantages and disadvantages. The calculation process of single factor evaluation method was the simplest. Its evaluation results could identify pollutants that had great impacts on water quality and analyze the general situation of effluent environmental quality. Nemerow index method took into account the most serious pollution factors and the average value， and the improved Nemerow index method was suitable for understanding the whole pollution situation of water quality. Through fuzzy mathematics method， water quality evaluation was made by calculating weight and membership degree， which reflected its non-linear relationship. The calculation process of the improved fuzzy mathematics method was the most complicated， and its evaluation result could determine the water quality index. According to the pollution situation in the study area， the fuzzy mathematics evaluation results were more consistent with the actual situation.

Key words Lower reaches of Futuan River;Quality evaluation of groundwater;Single factor evaluation method;Fuzzy comprehensive evaluation;Nemerow index method

作者简介袁杰（1984—），女，山东聊城人，高级工程师，硕士，从事水文地质、环境地质和地热地质研究。*通信作者，高级工程师，从事水文地质、环境地质和地热地质研究。

收稿日期 2021-01-21

当前我国的经济快速发展，因为前期采取的是先开采后治理的模式，导致很多地区地下水超采严重，地下水位不断下降，人为因素对地下水水环境的污染越来越严重[1]，因此地下水水质评价对于改善地下水环境就尤为重要。目前，常用的评价方法有单因子评价法[2]、内梅罗指数法[3]、改进的内梅罗指数法[4-5]、模糊数学法[6-9]、改进的模糊数学法[10-11]、物元分析法[12]、灰色系统评价法[13-14]、人工神经网络模型[15-16]、主成分分析法[17]等。

然而，地下水水质评价过程中会遇到比较模糊的问题，在众多的地下水水质评价方法中，实际应用时评价结果可能会出现偏差。笔者以日照市傅疃河下游地区为例，采用单因子评价法、内梅罗指数法、改进的内梅罗指数法、模糊数学法和改进的模糊数学法进行地下水水质评价，并对这几种评价方法所得结果进行比较，最后提出对工作区地下水水质评价较合理的评价方法，旨在为地下水环境的治理提供参考。

1 研究方法

1.1 单因子评价法

参照《地下水质量标准》（GB/T 14848—2017），根据评价指标的限值范围确定每一个指标的质量类别，在单指标评价的基础上，将结果最差的类别确定为该组地下水质量综合评价结果，并指出最差类别的指标[18]。

1.2 内梅罗指数法

内梅罗指数法是目前应用较多的地下水水质评价方法之一，其计算公式如下：

N=N2 max+N2 ave2（1）

N ave=1mmj=1N j（2）

式中，N为评价因子综合指数，N j为评价因子单项指数。

内梅罗指数法考虑了最大污染因子，但在实际应用中有些重金属不容易去除，会影响水的饮用，因此对内梅罗指数法进行了改进。

按以下公式计算评价因子的权重值：

H i=C imaxC i（3）

V i=H ini=1H i（4）

式中，H i为评价因子的相关性比值，V i为评价因子的权重，C i为评价标准的标准值，C imax为所有评价因子标准值的最大浓度。

按照以下公式计算内梅罗指数：

N j=（N2 max+N w）2+N2 ave2（5）

式中，N j为评价因子的修正指数，N w为权重最大值所对应的评价因子指数。

通过对改进前后公式的对比可知，改进的内梅罗指数法综合考虑了所有评价因子的权重问题，在一定程度上削弱了最大值对计算结果的影响。

1.3 模糊数学法

模糊数学法是根据模糊数学理论的一种定量评价方法，通过模糊描述和隶属度来表示地下水各等级的隶属关系，利用评价因子的隶属度矩阵和对应的权重矩阵的复合运算得出最终隶属度，进而对研究区的水质进行评价。

1.3.1 确定隶属度。

当j=1时，得出：

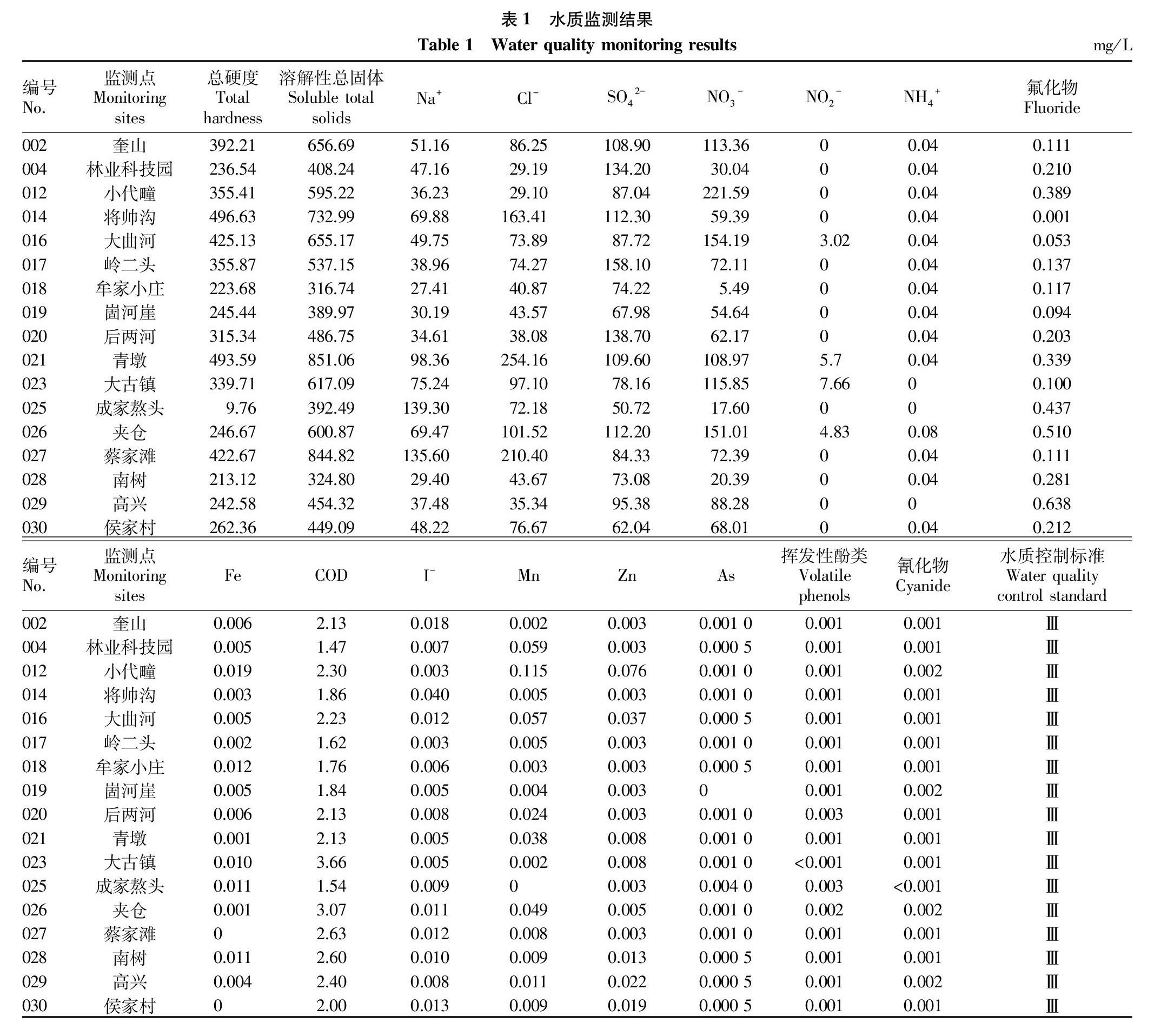
R ij=1，C i≤s ij

s ij+1-C is ij+1-s ij，s ij

0，C i>s ij+1（6）

当1

R ij=0，C i≤s ij-1

C i-s ij-1s ij-s ij-1，s ij-1

1，C i=s ij

s ij+1-C is ij+1-s ij，s ij

0，C i>s ij+1（7）

当j=5时，得出：

R ij=0，C i≤s ij-1

C i-s ij-1s ij-s ij-1，s ij-1

1，C i>s ij，i=1，2，…，n，j=1，2，…，n（8）

式中，n为污染因子数;j为水质级别数;s ij为污染因子第j级的标准浓度;C i为某一样品一种污染因子（x）的浓度。

在此基础上，构建几种评价因子的隶属度矩阵：

S（1） m×n=

R 11（x）…R 1m（x）

R n1（x）…R nm（x）

（9）

1.3.2 确定因子的权重。

根据评价因子对水质的贡献程度，确定评价因子的权重，进而得到权重矩阵W i：

R i=C imj=1s ij（10）

W i=R ini=1R i（11）

W 1×n=[W 11，W 12，…，W 1n]，

其中ni=1W i=1。

式中，R i為评价因子的相关性比值，W i为评价因子的权重值。

将权重矩阵乘以相关性比值，得到隶属度矩阵，其中最大隶属度所在等级代表着水样的整体级别，进而进行地下水安全评估。

1.3.3 隶属度的改进。

根据隶属度，引进综合模糊综合评价指数Z（k），达到改进隶属度的目的：

Z（k）=5n=1nB* n/5n=1B* n（12）

B* n=B n（x）-B n（x） minB n（x） max-B n（x） min（13）

式中，k为水样编号;B n（x）为n等级隶属度。

2 研究区概况

傅疃河为日照市最大的独流入海河流，发源于五莲县境内韩家窝洛子西北约2 km的大马鞍山，海拔417.8 m，主河道长约51.5 km，流域面积1 066.4 km2[19]，主要河流有崮河、大曲河、南湖河、三庄河等。区内主要出露地层为第四系，主要构造为日照断裂，断裂走向40°～45°，倾向南东，倾角70°～80°，规模较大，从研究区中部穿过。区内地下水类型主要为松散岩类孔隙水和基岩裂隙水。第四系松散岩类孔隙水补给方式主要为大气降水入渗补给、上游河谷地下水的侧向径流补给、河水入渗补给，基岩裂隙水以大气降水入渗补给为主[20]。

傅疃河河流冲积形成的中下游河谷盆地区地下水是日照城区工业用水、生活用水和农业用水的重要供水水源[20]，因此对傅疃河地下水水质评价尤为重要。

3 水质监测数据及评价结果

3.1 水质监测数据

分析资料选取日照市地下水监测中傅疃河下游17个监测点2018年10月丰水期监测数据为基础，选取溶解性总固体、总硬度、Na+、Cl-、SO 42-、NO 3-、NO 2-、NH 4+、氟化物、Fe、I-、Mn、Zn、As、化学需氧量（COD）、挥发性酚类、氰化物，共17个指标（表1）。

由表1可知，傅疃河下游地区各监测点水质大部分化学组分含量中等（Ⅲ类限值以内），可用于集中式生活饮用水，仅有部分监测点水样的NO 3-、Cl-、COD浓度偏高，水质总体情况较好。

3.2 评价结果

分别采用单因子评价法、内梅罗指数法及其改进方法、模糊数学法及其改进方法对傅疃河下游地区水质进行评价，得出分析结果（表2、图1）。

根据单因子评价法原理计算结果可知，地下水水质Ⅱ类水1处，占5.88%;Ⅲ类水7处，占41.18%;Ⅳ类水4处，占23.53%;Ⅴ类水5处，占29.41%。

内梅罗指数法计算结果表明：区域内地下水水质集中在Ⅱ类和Ⅲ类水，其中Ⅰ类水1处，占5.88%;Ⅱ类水7处，占41.18%;Ⅲ类水7处，占41.18%;Ⅴ类水2处，占11.76%，未见IV类水分布。水质整体处于优良水平，而改进的内梅罗指数法评价结果表明水质级别也集中在Ⅱ类和Ⅲ类水，占76.47%，未见V类水分布。内梅罗指数法及其改进方法评价结果表明水质类型一致的监测点占58.9%，不一致的监测点占41.1%，其水质级别总体上变好。比如奎山监测点NO- 3浓度超标，为Ⅳ类，其对2种方法的评价结果产生了影响，内梅罗指数法评价结果为Ⅳ类，而改进的内梅罗指数法评价结果为Ⅱ类水，其在加权过程中削弱了最大值的影响，因此其结果也更加客观。

模糊数学法计算结果显示，Ⅰ、Ⅱ、Ⅲ、Ⅴ类水分布差别不大，而改进的模糊数学法水质类别集中在Ⅱ类和Ⅲ类，占比88.24%，评价结果相似度较高，但改进的模糊数学法可以給出精确的指数，这对于同一级别的水质类别可以更准确地进行对比。

从表2和图2、3可以看出，5种水质评价法均能反映地下水各监测点的水质变化，说明这几种方法在一定程度上均可用于地下水水质评估，但又各有优缺点。

（1）单因子评价法更多地突出某一因子对水质污染的贡献，即使有一个指标为超Ⅴ类标准，而其他指标均为Ⅰ类时，水质评价结果也为Ⅴ类，因此单因子评价法适合用于确定主要污染物，评价方法相对来说是最简单的，但不能反映其地下水污染的整体状况。

（2）内梅罗指数法是综合考虑了最大污染因子和所有因子指数的平均值，未考虑各个因子的权重问题，涉及评价因子的降解情况，因此评价结果有失偏颇。

（3）改进的内梅罗指数法。改进的内梅罗指数法在内梅罗指数的基础上引进了评价因子的权重值，在一定程度上削弱了最大值对计算结果的影响，使其评价结果更加合理。

（4）模糊数学法。模糊数学法通过各因子之间的非线性关系来体现其模糊性，通过隶属度和权重关系来计算水质评

价，其结果不仅考虑了各因子的危害水平，而且考虑了各个因子之间的非线性关系，使评价结果趋于合理，但是因为在权重赋值过程中，人为的主观因素影响较大，使评价结果受到一定的影响。

（5）改进的模糊数学法。在模糊数学法的基础上，对隶属关系进行了改进，改进后评价的结果能准确给出地下水的水质指数，可以对同一级别的水质类别进行排序。

综合以上几种评价方法，从计算过程来看，单因子评价法的计算过程最简单、计算量最小，而改进的模糊数学法计算过程最复杂、计算量较大。虽然改进的模糊数学法能对同一级别的若干水样进行优劣对比，但结合傅疃河地区实际情况，模糊数学法评价结果与实际调查过程中的污染情况相一致。

4 结论

以日照市傅疃河流域下游地区各监测点水质评价为例，分别采用单因子评价法、传统内梅罗指数法、改进的内梅罗指数法、模糊数学法和改进的模糊数学法进行了对比。结果表明：单因子评价法适用于确定对水质影响较大的污染物;内梅罗指数法因为考虑到最大污染物的影响，其在结果中可能使得结果偏高。改进的内梅罗指数法、模糊数学法和改进的模糊数学法都引用了权重值，在一定程度上保证了水质评价结果的可靠性和准确性。改进的内梅罗指数法适用于了解监测点的整体污染状况;

模糊数学法通过隶属度来体现其非线性关系，使得结果更加合理。改进的模糊综合评价法在原有的基础上对结果从算法上进一步改进，使结果具有一定的连续性，可以将同种类别的水样细化对比，评出优劣。结合傅疃河下游地区实际调查结果可知，模糊数学法与其他4种评价方法相比，评价结果对研究区地下水水质的拟合度较高，稳定性较好，最适宜傅疃河流域下游地区地下水水质评价。

参考文献

[1] 李扬，窦炳臣，陈振，等.地下水水质评价与预测方法综述[J].山东国土资源，2015，31（8）：33-36.

[2] 郑琨，张蕾，薛晨亮.单因子指数法在水质评价中的应用研究[J].地下水，2018，40（5）：79-80.

[3] 罗芳，伍国荣，王冲，等.内梅罗污染指数法和单因子评价法在水质评价中的应用[J].环境与可持续发展，2016，41（5）：87-89.

[4] 杨磊磊，卢文喜，黄鹤，等.改进内梅羅污染指数法和模糊综合法在水质评价中的应用[J].水电能源科学，2012，30（6）：41-44.

[5] 陈朋，王家鼎，袁亮，等.修正内梅罗指数法和模糊综合评判法在凤凰镇地下水水质评价中的应用[J].水土保持通报，2017，37（2）：165-170.

[6] 付恩光，吴光伟，李同心.模糊数学在海（咸）水入侵水质评价中的应用：以寿光地区为例[J].山东国土资源，2017，33（7）：66-70.

[7] 万金保，李媛媛.模糊综合评价法在鄱阳湖水质评价中的应用[J].上海环境科学，2007，24（5）：215-218.

[8] 王艳秋，王辉，张震斌.模糊综合评判法在阜新水质评价中的应用[J].辽宁工学院学报，2006，26（1）：4-6.

[9] 潘峰，付强，梁川.模糊综合评价在水环境质量综合评价中的应用研究[J].环境工程，2002，20（2）：58-61.

[10] 傅金祥，陈喆，马兴冠，等.改良模糊综合评价法在水质评价中的应用[J].环境工程，2011，29（6）：120-123.

[11] 杨鹏，计量，朱伟，等.沂源县地下水水质评价及成因分析[J].节水灌溉，2018（12）：65-69.