轮足混合式消防机器人的结构设计与分析
2021-09-27郭安福张海琦
姜 涛,郭安福,李 进,陈 清,张海琦
(聊城大学 机械与汽车工程学院,聊城 252059)
0 引言
随着社会经济的发展以及大型石油化工企业和隧道、地铁等建设项目的不断增加,危险化学品和放射性物质泄漏以及燃烧、爆炸、坍塌事故也在增多[1~3]。特别是一些特殊的企业发生的火灾,如化工企业、纺织企业等,具有突发性强、燃烧猛烈等特点,并且火灾过程中会产生大量的有毒气体,严重地危害周围群众和救灾人员的生命安全[4~6]。因此,研发成本低、功能强、经济实用的消防灭火机器人具有重要意义。
最早的消防机器人是1986年日本东京消防厅“彩虹5号”机器人,可代替消防人员进入复杂地形灭火[7]。2006年,由挪威科学家研制出一种蛇形消防机器人,进入消防救援人员无法进入的场所实施灭火工作[8,9]。2008年,由德国马格德堡一施腾达尔大学设计开发了一种球形新型消防机器人“甲虫奥勒(OLE)”,可以用来监测森林火灾[10]。在2012年美国HoweandHowe Techonologies公司开发了一款消防机器人Thmite,可解决列车脱轨事故中由核燃料和化学燃料产生的火灾[11]。
近年来,我国的消防机器人研究得到了政府和有关部门的支持,如西北工业大学彭涛提出一种高空消防机器人模糊控制设计方案,但其移动速度和材料制备都有很大的难度[12]。南京林业大学的姜树海设计了一种用于森林消防的六足机器人,但在其运动过程中关节力矩过大会对驱动电机造成一定程度的损害[13]。上海交通大学机器人研究所的徐正飞提出集火场探测、消防以及有毒、易燃、易爆气体场所探测等多种功能于一体的遥控关节式移动机器人控制系统,但目前仍停留于理论研究[14]。
综合国内外消防机器人的研究现状,发现目前对于老旧楼道、狭窄隧道的火灾问题仍处于理论研究状态,无法有效地对火灾进行扑灭。
针对此问题,本文设计了一种可在四驱轮式和双足步态行走自由切换,并可实现全方位喷射的消防机器人。首先对机器整体结构进行设计分析。其次,对主要零部件进行SolidWorks建模仿真分析,采用MATLAB/Simulink对行走装置进行振动仿真分析。最后搭建样机进行实验,验证装置设计合理性。
1 结构设计与工作原理分析
1.1 整体结构设计
本机器主要由四驱行走装置、步态行走装置、灭火喷射装置、转臂执行装置、火源检测装置、储水装置、电子与控制系统等组成,其装置整体设计如图1所示。
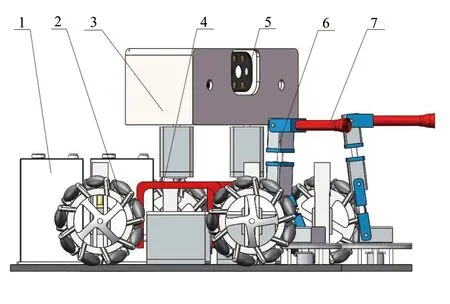
图1 机器整体结构图
1.2 工作原理
机器的工作原理如图2所示,其工作流程如下。
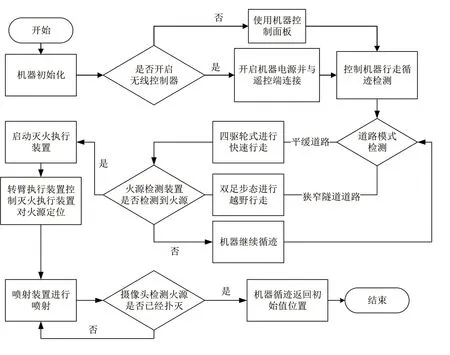
图2 消防机器人工作原理图
1)操作人员开启机器、遥控端电源,操作人员通过遥控端发送指令控制车身的行走,进入火灾现场后,启动道路与火源检测模式。
2)在道路检测模式下,机器可在平地与狭窄隧道的道路上,进行轮式与步态越野避障行走。
3)在火源检测模式下,火源检测装置实时检测火源。当火源检测装置检测到火源时,STM32芯片控制消防机器人规划路线,循迹至火源位置。
4)循迹至火源位置后,消防机器人停止运动,开始定位火源,启动灭火喷射装置。
5)根据摄像头采集的图像,转臂执行装置控制灭火喷射装置对指定火源进行灭火喷射,其喷射形成有效的包围圈,可有效对火源扑灭。
6)在灭火过程中摄像头实时采集图像,通过图像处理算法检测火源是否被扑灭,如果火源扑灭,继续寻找下一处火源位置,一直到火源全部扑灭后返回至初始位置。
2 消防机器人的结构设计
2.1 行走装置的设计
本机器的行走装置三维模型图如图3所示,行走装置主要包括四驱行走装置和步态行走装置两部分。本设计在传统的四驱轮式基础上,增添步态行走模式,通过摄像头对采集图像进行处理,检测道路模式,在平缓道路上切换至四驱轮式状态,提高机器移动的速度,在狭窄隧道的道路上或老旧楼道上切换至步态交替行走。
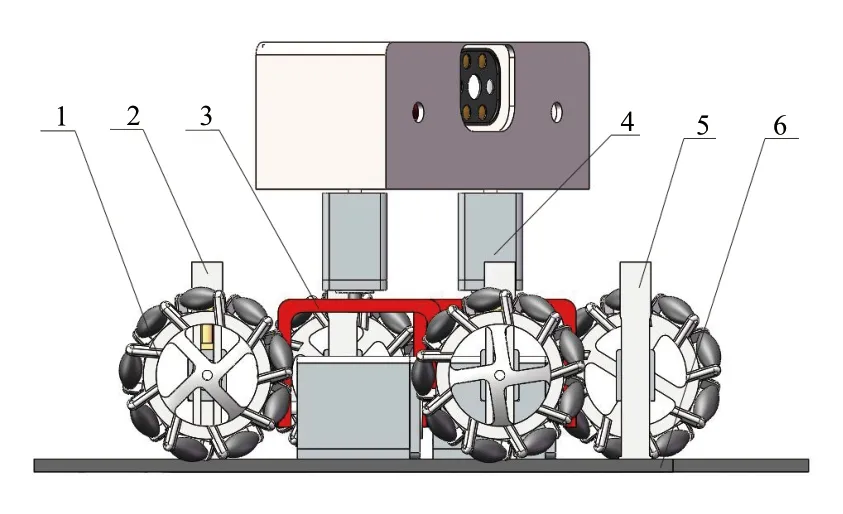
图3 行走装置模型图
2.1.1 四驱行走装置的设计
四驱行走装置采用伸缩气缸和麦克纳姆轮相配合的设计,其三维模型如图4所示。通过摄像头采集图像进行处理判断道路模式,在平缓道路上,伸缩气缸通过支架连接步进电机控制麦克纳姆轮上下运动,改变运动方式。
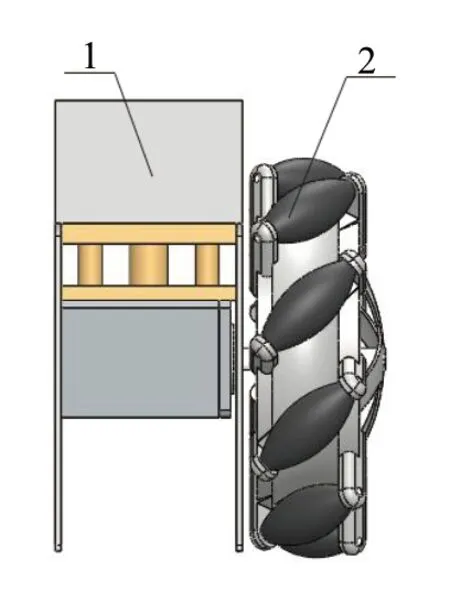
图4 四驱行走装置模型图
2.1.2 双足行走装置的设计
针对传统消防机器人无法进入老旧楼道、狭窄隧道等地形复杂的地区的问题。本机器对行走装置进行仿人型的足式步态设计,使其可在老旧楼道的台阶或狭窄隧道的道路上行走,提高消防机器人越野避障的能力,其三维模型如图5所示。
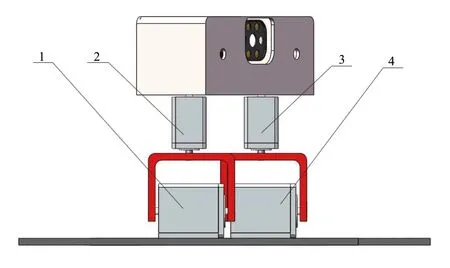
图5 双足行走装置模型图
2.2 转臂执行装置的设计
在整个系统结构中,转臂执行机构为本机器的独特设计。转臂执行装置由主转台、关节1、关节2、关节3、喷射器等组成。转臂运行时,主转台旋转,带动关节1和关节2运动,关节3随之做旋转运动,控制安装在关节3末端的机械臂做伸缩和旋转运动,通过喷射器对火源形成有效的包围圈。根据中央控制器STM32的指令信号,控制水泵和流量阀进行灭火,三维模型如图6所示。
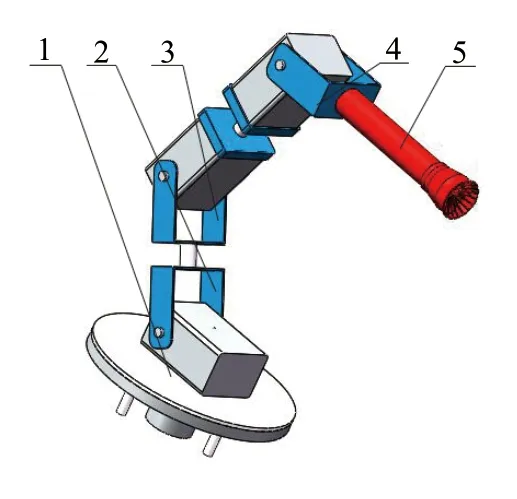
图6 执行装置示意图
3 主要零部件建模仿真分析
3.1 四驱行走装置建模仿真
四驱行走装置是本机器的核心装置,为保证其稳定性,本文采用SolidWorks对固定伸缩气缸的U型支架进行Simulation静应力分析,其结果如图7所示,由图7可知。
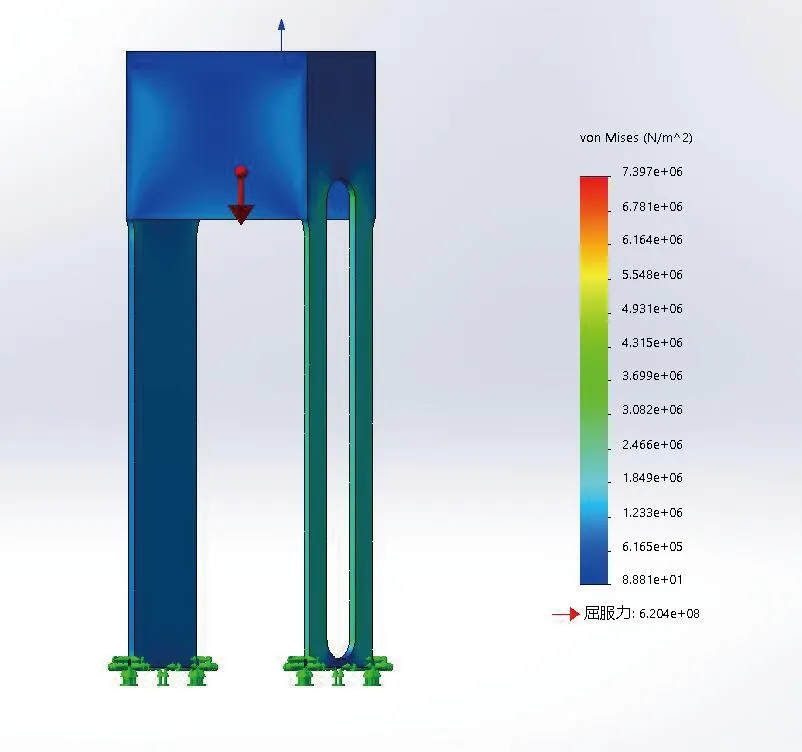
图7 有限元分析
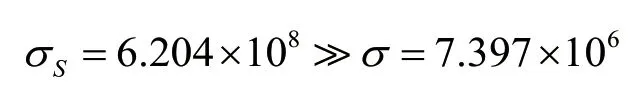
式中:
σs为材料的最大屈服应力(N/m2)
σ为材料的最大变形应力(N/m2)
由以上数据可知设计的U型支架其应力远小于材料屈服应力,满足零件的设计要求,可保证气缸在垂直方向的稳定运行。
为进一步保证气缸在垂直方向的运动稳定性,采用Motion动力学对四驱行走装置的轨迹路线进行分析,分析结果如图8所示。由图8可知车轮在垂直方向为线性运动,气缸推杆的位移量为0.48m,运行时间为3.2s,运行速度为0.15m/s。
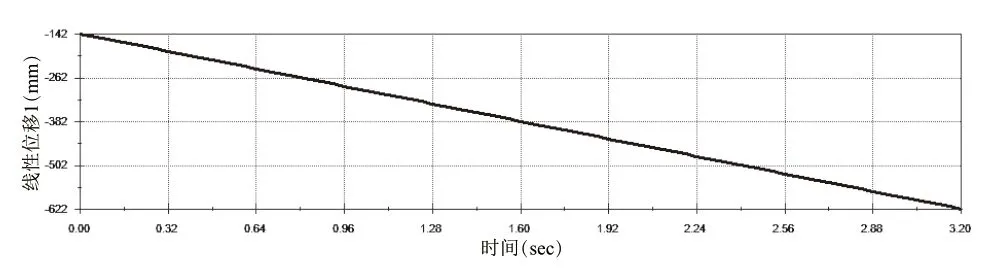
图8 四驱行走装置运动学分析
3.2 行走装置的Simulink振动仿真分析
3.2.1 四自由度机器振动模型
机器在运动的过程中由于路面的不平度和车轮运动方向的转变会导致局部产生剧烈的振动影响其稳定性[15,16]。因此研究机器振动,对主要参数合理设计具有重大意义[17~19]。
将机器简化为4自由度的振动模型,分别为机器本身的垂直和俯仰两个自由度、车轮前后轴两个自由度,振动模型如图9所示。
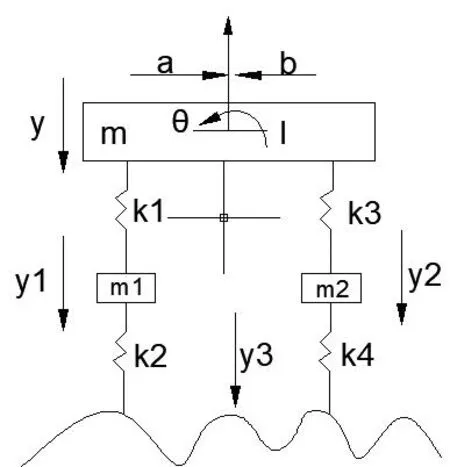
图9 4自由度振动模型
图9中:
m为机器重量(kg);
m1为前轮重量(kg);
m2为后轮重量(kg);
I为车身绕质心的转动惯量(kg.m2);
θ为机器质量转角(rad);
a、b为前后轴到质心的距离(m);
k1.Ak3为前后轮胎刚度(N.m-1);
k2.Ak4为前后悬架刚度(N.m-1);
y、y1、y2为机器、前轮、后轮位移量(m);
y3为路面不平度的位移量(m)。
简化4自由度的振动模型并进行受力分析,根据受力分析结果建立平衡方程如下。
机器受力平衡方程为:
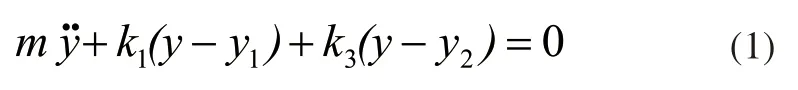
前轴前轮受力分析为:
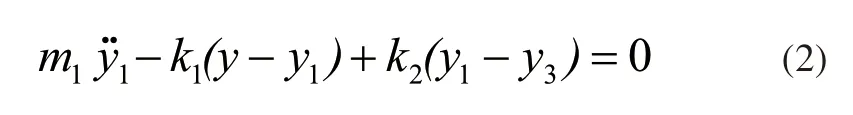
后轴后轮受力分析为:
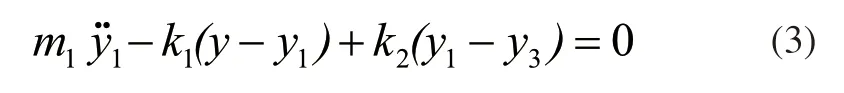
力矩平衡方程为:
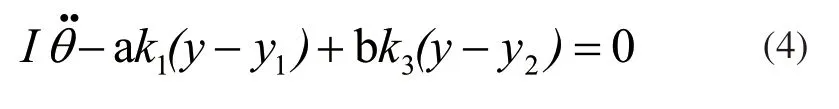
对于前后轴上方的垂直位移有如下关系:
前轴:
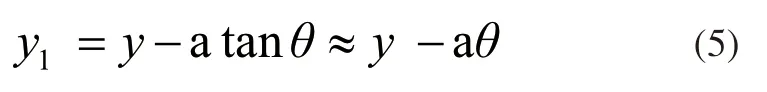
后轴:
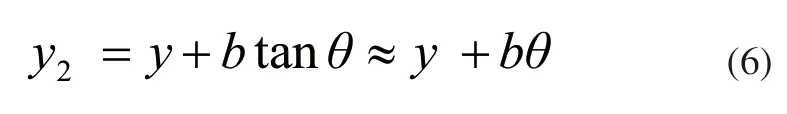
整理式(1)~式(6)得:
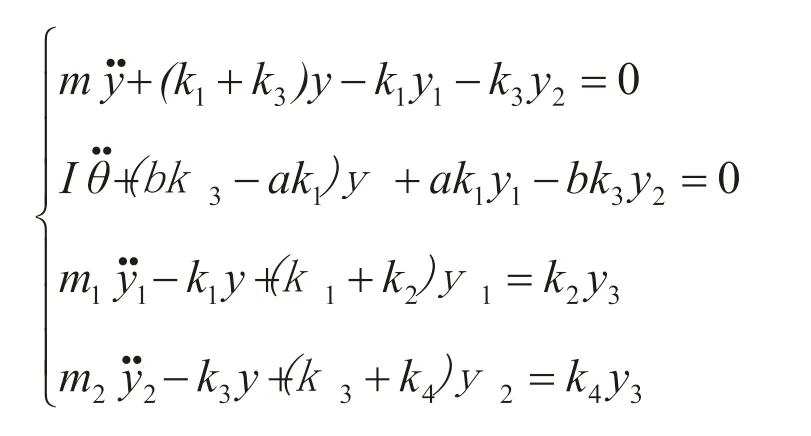
将上式简化为质量矩阵可得:
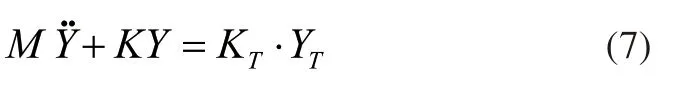
式中:
M为机器的质量矩阵;
Y为机器各自由度的位移量;
K为机器的刚度矩阵;
KT为麦克纳姆轮的刚度矩阵;
YT为路面不平度的位移量。
可得:
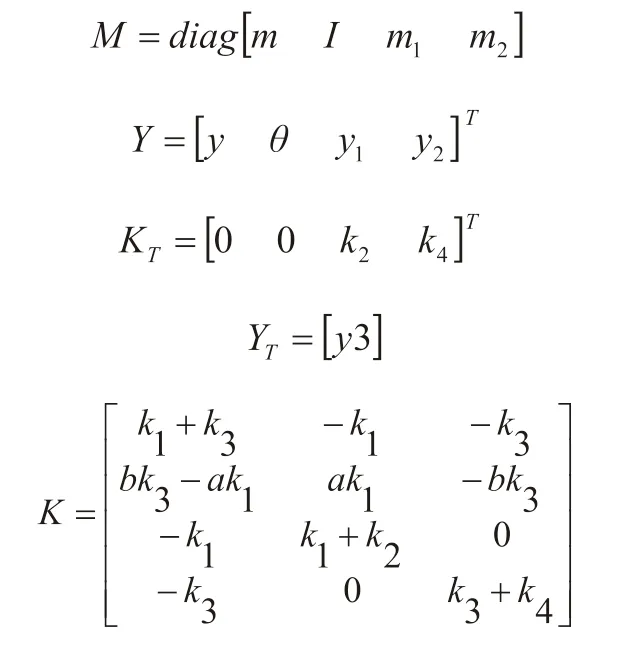
对式(7)两侧同取拉斯变换可得:
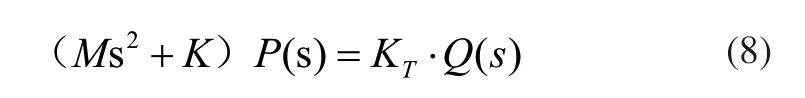
化简可得传递函数矩阵为:
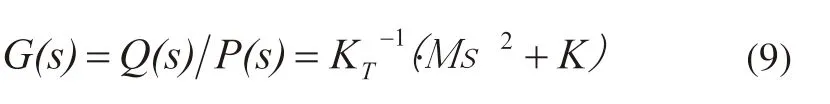
用jw代替s算子可得机器的频率响应函数。
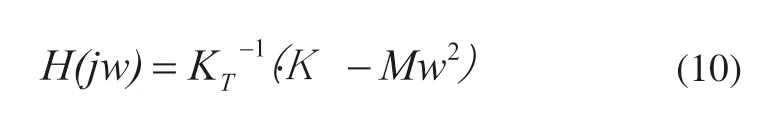
3.2.2 四自由度机器振动分析
采用MATLAB/Simulink软件,将上述4自由度振动模型转化为计算机仿真模型,机器仿真参数如表1所示,仿真模型如图10所示。
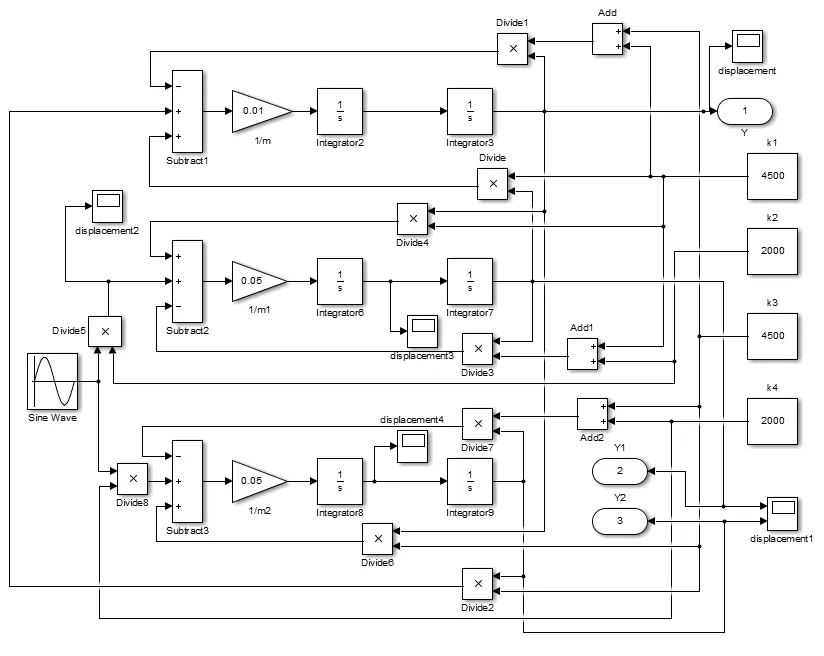
图10 Simulink仿真模型图
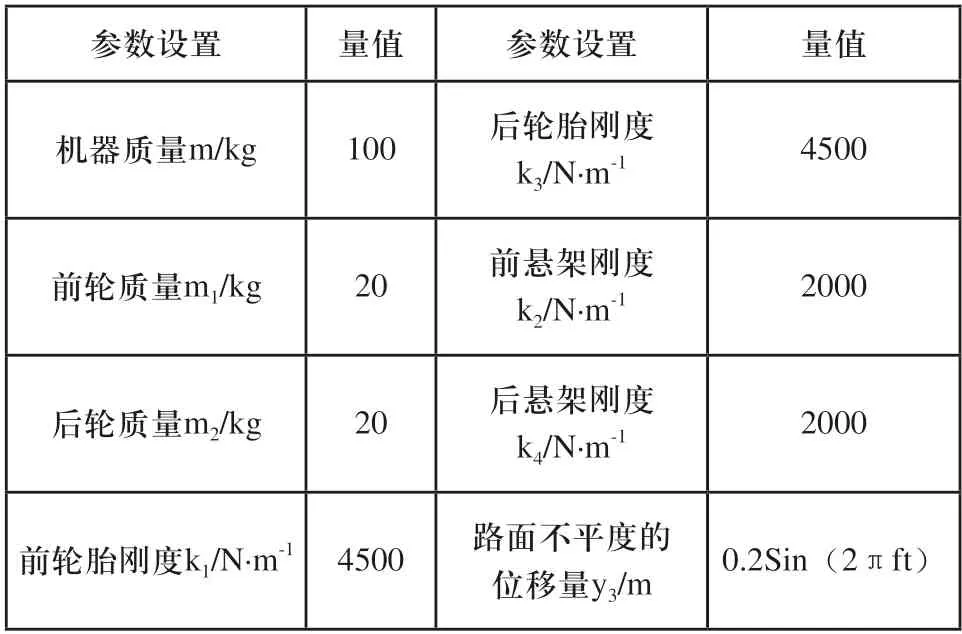
表1 机器仿真参数表
机器在运动过程中,由于路面模型和行驶速度的不同,造成的路面不平度激励是不同的。为了更好的进行仿真实验,将路面模型简化为正弦曲线,其数学模型为y3=0.2sin(2πft),取f=10Hz得到的仿真结果如图11所示。从图11可以看出,机器行走的振动曲线为简谐振动,其振动的最大值分别为y=0.02059m、y1=y2=0.03188m。
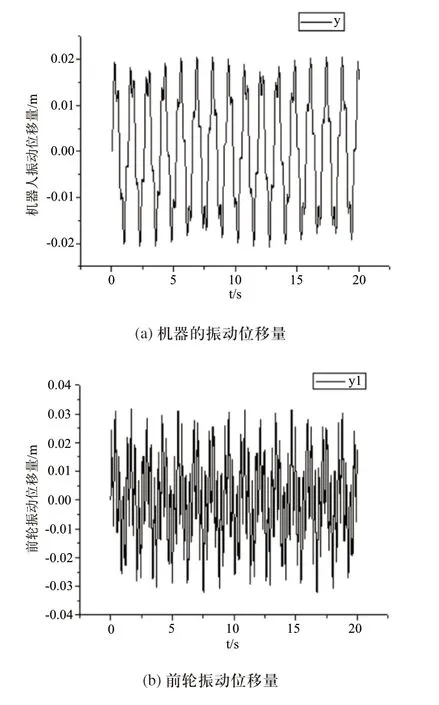
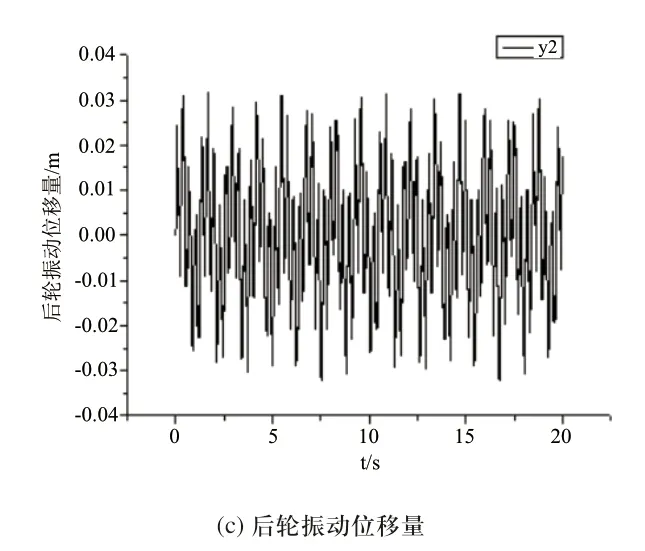
图11 机器振动位移曲线
由此可知本机器的垂直自由度振动位移量完全可保证机器运动过程的平顺性和稳定性。
4 实验验证
轮足混合式消防机器人双足行走装置的样机模型如图12所示,考虑到双足算法、行走速度对双足行走平衡能力的影响,本文在实验室环境下对该消防机器人进行双足步态算法、行走速度的实验分析。消防机器人在一定区域内巡逻,通过双足步态行走跨越障碍物。进行多组实验测试机器人的平衡能力,实验数据如表2所示,在伺服舵机分步执行值x=100的条件下,改变机器人的转角速度,进行多组实验,实验数据如表3所示。

图12 消防机器人双足行走转置样机模型
根据表2实验结果可知采用该分步执行步态算法其平衡率高达98.8%,相比于延时函数控制舵机其平衡能力增强3.6%,可减少事故的发生。由表3可知,舵机转角速度越快,机器人摔倒的次数越多,平衡率越低。
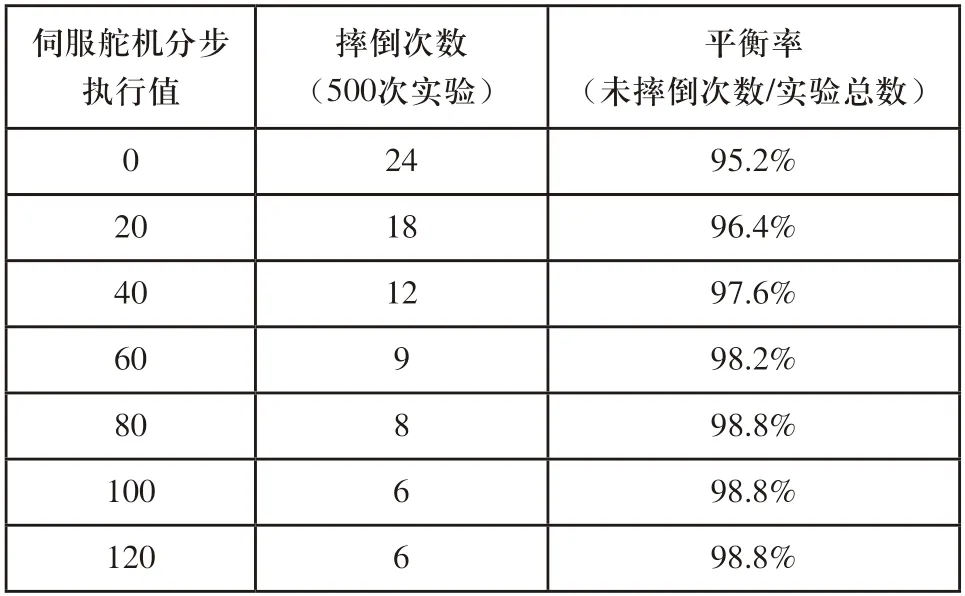
表2 双足步态算法实验
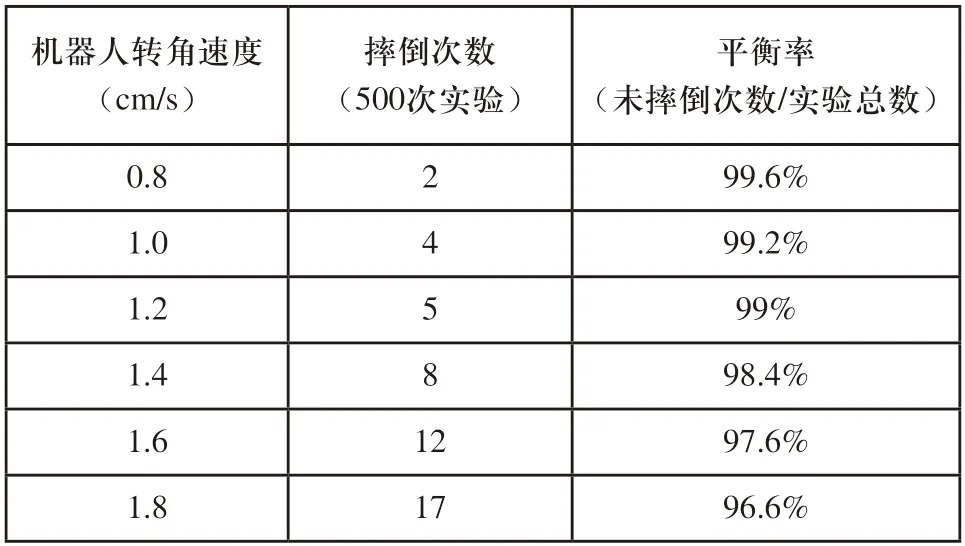
表3 机器人转角速度实验
5 结语
1)对机器的整体结构进行设计,并对主要零部件行走装置和转臂执行装置进行结构设计。
2)采用三维SolidWorks进行建模仿真分析。对四驱行走装置进行建模分析,通过静力学应力分析可知其应力小于材料屈服应力,完全符合使用要求。采用Motion动力学对其运动轨迹进行分析,结果表明:下落时间为3.2s,运行速度为0.15m/s,可保证车轮在垂直方向的线性运动
3)对机器的行走装置进行MATLAB/Simulink仿真分析,结果表明:机器最大的垂直自由度的振动位移量ymax=0.02059m。由此可知该设计的机器垂直自由度的振动位移量小,可保证机器在运动过程的平顺性和稳定性。
4)通过实验表明:在舵机分步执行值为100时,其平衡率高达98.8%,转角速度为0.8cm/s时,其平衡率达99.6%,由此可知该算法可有效提高机器人的平衡能力,减少事故的发生。
