浅谈高中数学解题中代换法的应用

王 平

(江西省赣州市南康区第三中学 341400)

高中数学教学中应深刻认识到解题方法的重要性.良好的解题方法能够获得事半功倍的解题效果，因此教学中应注重总结高中数学常用的解题方法，其中代换法在解题中有着广泛的应用，因此教学中应结合教学进度做好代换法的应用讲解，使学生掌握代换法的应用技巧，能够在解题中以不变应万变.

一、用于解答三角函数习题

A.5 B.3 C.1 D.不确定

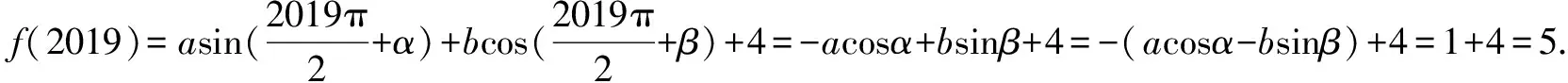
故选A.

点拨运用代换法解答三角函数习题应注重三角函数周期、恒等变换等知识的应用，尤其通过化简已知条件以及要求解的问题，对共同的部分加以合理代换，以顺利得出正确结果.

二、用于解答求范围类的习题

例2 已知x,y为正实数，满足x+2y+4=4xy，且当不等式(x+2y)a2+2a+2xy-34≥0恒成立时，实数a的取值范围为( ).

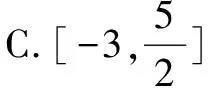
分析该题目难度较大，看似无从下手，若认真观察给出的已知条件，找到已知条件中的共同部分，使用代换法可迅速加以突破.

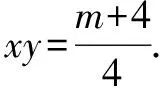
整理,得m2-2m-8≥0.解得m≥4或m≤-2.

又因为m>0，因此m≥4.

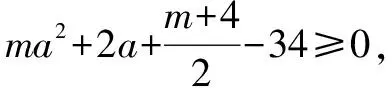
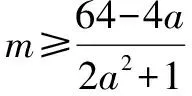
故选D.

点拨运用代换法求解范围的习题，可结合题干条件以及解题经验，找到需要代换的部分.同时，需要注意的是在代换的过程中应注意参数、表达式的取值范围，从而对最终的结果进行合理取舍.

三、用于解答最值类的习题

A.1 B.2 C.3 D.4

分析解答该题需结合题干充分挖掘隐含条件，而后运用代换法进行转化，最后使用基本不等式知识求解.

因为二次函数f(x)=ax2+bx+c(b>a>0)的值非负，所以a>0，Δ=b2-4ac≤0，即b2≤4ac.

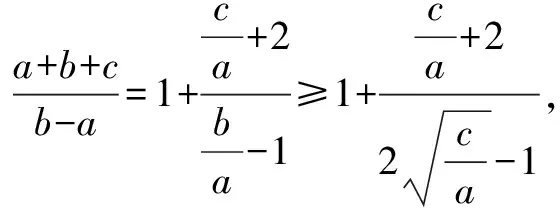
点拨运用代换法解答最值类的习题，应注重充分挖掘题干中的隐含条件，认真思考代换后采用哪些知识进行求解.一般情况下，代换后可考虑使用基本不等式以及函数单调性求解最值.

四、用于解答不等式类的习题

分析因为函数f(x)的表达式中带有根式，不利于计算，因此，可考虑采用代换法进行处理.

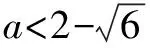
(3)当a≥1时，g(a)=f(1)=a2-2a+5.由g(a)>8，可得a2-2a-3>0，解得a<-1或a>3，其中a<-1舍去.

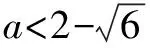
点拨解答不等式类型的习题时如表达式中含有根式，应能迅速想到运用代换法进行处理，化陌生为熟悉，然后运用所学进行严谨推理，尤其当涉及到分类讨论问题时，应注重讨论的条理性，防止漏掉情况.

高中数学教学中为提高学生的解题能力，使其认识到代换法的重要性，并能灵活用于解答各类数学习题，应注重为学生讲解代换法的相关理论，使学生掌握在解题中应用率较高的代换形式.同时，课堂上注重为学生示范代换法的具体应用，并鼓励其做好听课的总结，使其真正掌握这一重要的解题方法.