基于主成分与多元线性回归分析的新疆兵团第八师灌溉用水有效利用系数影响因素

王 丽，黄 勇，丁 涛，陶洪飞，周 洋

本文以提高新疆兵团第八师灌溉用水有效利用系数为目的，对其影响因素进行主成分分析[1]，将原来多个可能存在共线关系的影响因素数据简化为少量新的综合指标，建立多元线性回归模型，对今后的灌溉用水有效利用系数进行模型预测。

1 第八师农业灌溉情况

新疆兵团第八师农业灌溉灌区划分为两个大型灌区，3个中型灌区，1个纯井灌区，无小型灌区[2]，具体划分情况见表1。

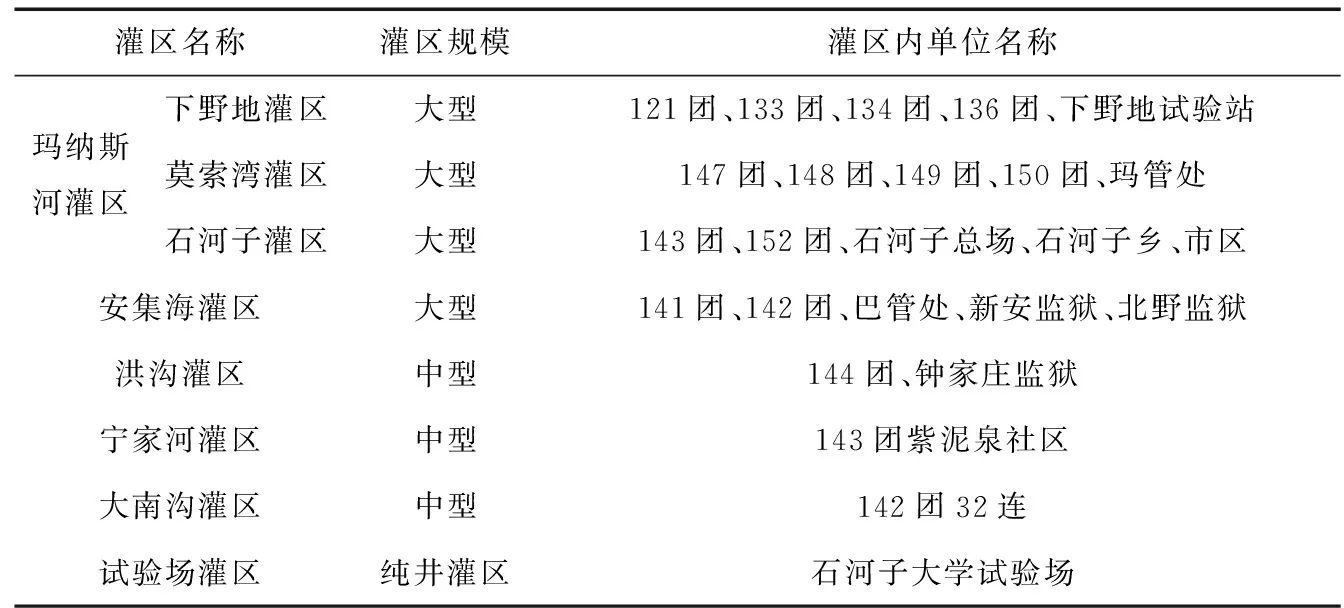
表1 第八师各灌区情况Tab.1 The irrigation areas of the eighth division

2 影响因素分析

在选取第八师灌溉水影响因素时，结合第八师各灌区的现状农业情况，综合考虑自然因素、灌区用水管理水平、节水灌溉情况、渠系防渗、田间节水等方面，全面概括各主要因素，然后将各影响因素指标量化，便于分析各影响因素对灌溉用水有效利用系数的影响程度。影响因素指标选取时应符合以下原则：各影响因素全面概括性；确保影响因素没有被重复考虑；各影响因素可量化性；选取的影响因素符合被研究灌区的实际状况。

2.1 指标体系的建立

为了全面客观选取影响因素，既要收集第八师多年的灌区基础资料进行统计分析，又要咨询当地各灌区的相关专家。从整体最优化选取为目标出发，对自然因素、种植模式、管理因素以及高效节水灌溉因素进行量化分析、综合选取，建立关于影响因素的基础指标体系，见表2。

表2 影响因素指标体系Tab.2 Index system of influencing factors

2.2 主成分分析

主成分分析的主要作用是降维和简化数据结构，把原有的多个指标转化为少数几个代表性较好的综合指标，这少数几个指标能够反映原来指标大部分的信息，并且各个指标之间保持独立，避免出现重叠信息。

本文基于2008-2017年新疆兵团第八师各灌区农业灌溉基础数据，经过文献查阅、专家咨询，结合第八师灌区现状情况，选取灌溉面积、毛灌溉用水总量、棉花种植比、当年完成节水工程投资、累计达到节水灌溉工程面积、渠道衬砌率、降水量等影响因素进行主成分分析。通过主成分分析影响因素，有效降低了模型变量的维数，有效解决了影响因素共线、信息重叠给数据分析带来的困扰[3]。

通过Spss软件对各影响因素原始数据进行标准化处理消除量纲，通过主成分分析得到相关系数矩阵(表3)。从表3中可以看出，渠道衬砌率与灌溉面积、累计达到节水灌溉工程面积有较高相关性。说明它们在信息上重叠，用Spss提取出主成分综合指标来代替影响因素原始指标分析，可以有效避免重叠信息，并且各综合指标可以保持相对独立，可见采用主成分分析是比较合适的方法。

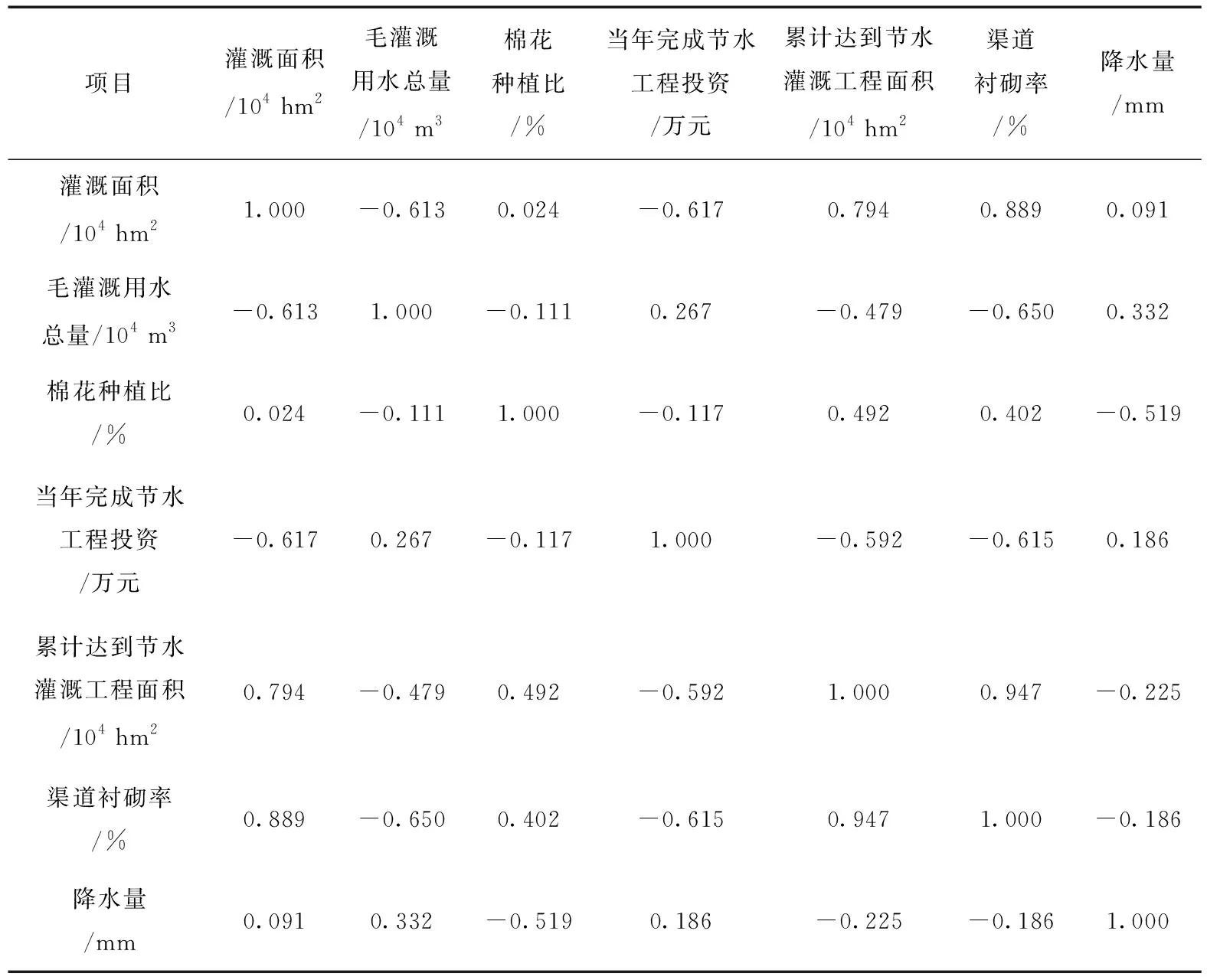
表3 相关系数矩阵Tab.3 Correlation coefficient matrix

通过表4中KMO和巴特利特检验结果可以得出，KMO等于0.611，大于0.5适合作因子分析；显著性P为0.002，小于显著性水平0.05，可以得出用主成分分析比较合适。

表4 KMO和巴特利特检验Tab.4 KMO and bartlett tests

通过表5中共同度分析结果可以看出，每个变量在每个共同因素负荷量的平方总和分别为0.958、0.478、0.762、0.519、0.873、0.962和0.756，说明主成分变量能够表达原始变量。

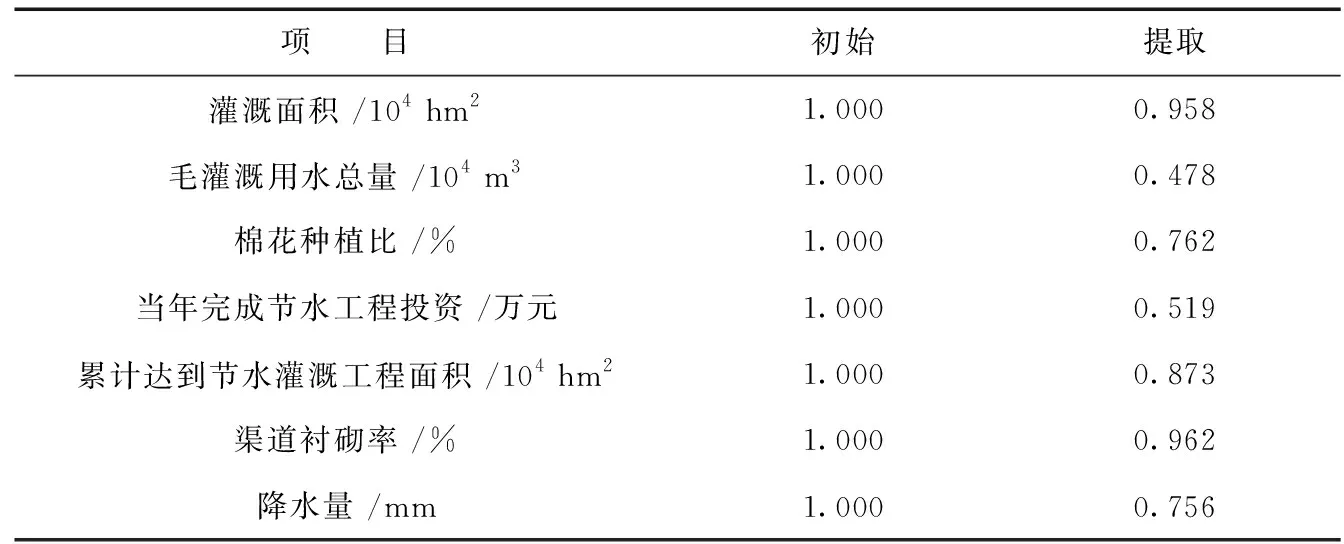
表5 共同度分析Tab.5 Common degree analysis

通过表6中主成分提取结果可以得到，提取两个主成分，特征值分别为3.826和1.483，前两个方差百分比为75.850，表明主成分分析结果比较理想。

表6 主成分提取结果Tab.6 Principal component extraction results

由因子荷载矩阵(表7)可知，灌溉面积、毛灌溉用水总量、当年完成节水工程投资、累计达到节水灌溉工程面积、渠道衬砌率在第一主成分上有较高荷载，第一主成分基本反映了这些信息；棉花种植比、降水量在第二主成分上有较高荷载，决定用两个新的变量代替原来的7个原始变量。但这两个新变量还不能从输出窗口直接得到，每一个荷载量表示主成分与对应变量的相关系数。

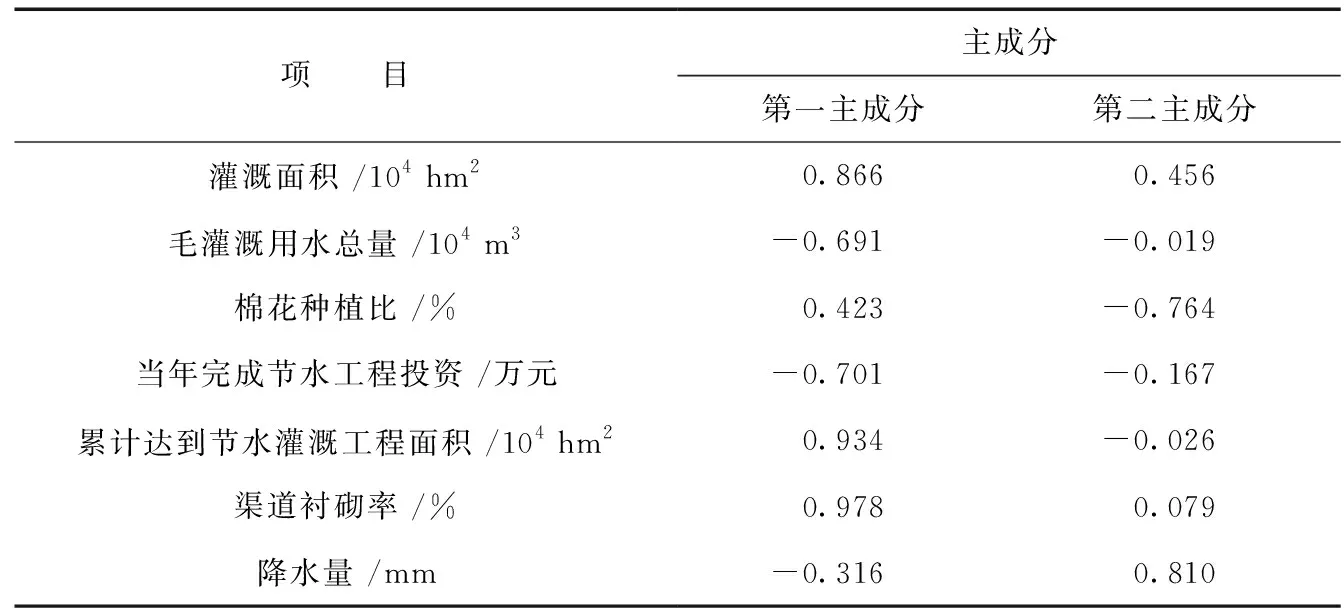
表7 因子荷载矩阵Tab.7 Factor load matrix

图1为主成分因子分析输出的碎石图，横坐标代表公共因子的个数，纵坐标代表公共因子的特征值。

图1 主成分影响因子碎石图Fig.1 Principal component influencing factor lithotripsy diagram

第一、第二主成分模型的表达式见式(1)、式(2)：

F1=0.44X1-0.35X2+0.22X3-0.36X4+0.48X5+0.5X6-0.16X7

(1)

F2=0.37X1-0.02X2+0.63X3-0.14X4-0.02X5+0.06X6+0.67X7

(2)

式中：F1为第一主成分；F2为第二主成分；X1为灌溉面积；X2为毛灌溉用水总量；X3为棉花种植比；X4为当年完成节水工程投资；X5为累计达到节水灌溉工程面积；X6为渠道衬砌率；X7为降水量。

主成分综合模型：

(3)

样本综合得分结果见表8。

表8 样本综合得分Tab.8 Composite sample score

由表9可以得出主成分荷载值，主成分荷载值反映了主成分与原指标之间的相关性。从表9可以得出，第一主成分中灌溉面积、渠道衬砌率、累计达到节水灌溉工程面积、当年完成节水工程投资、毛灌溉用水总量荷载值分别为0.964、0.955、0.881、0.718和-0.664；第二主成分中棉花种植比、降水量的荷载值为0.856和-0.868，说明第一主成分中灌溉面积、毛灌溉用水总量对灌水效率的影响比较大，同时累计达到节水灌溉工程面积、当年完成节水工程投资、渠道衬砌率对灌水效率的影响也比较显著。说明棉花种植比、降水量在第一主成分中占得比重较小，相对来说棉花种植比、降水量对灌水效率的影响程度较小，虽然影响程度小，但是第二主成分的贡献率也达到了21.191%，说明棉花种植比、降水量也是不能忽略的影响因素。

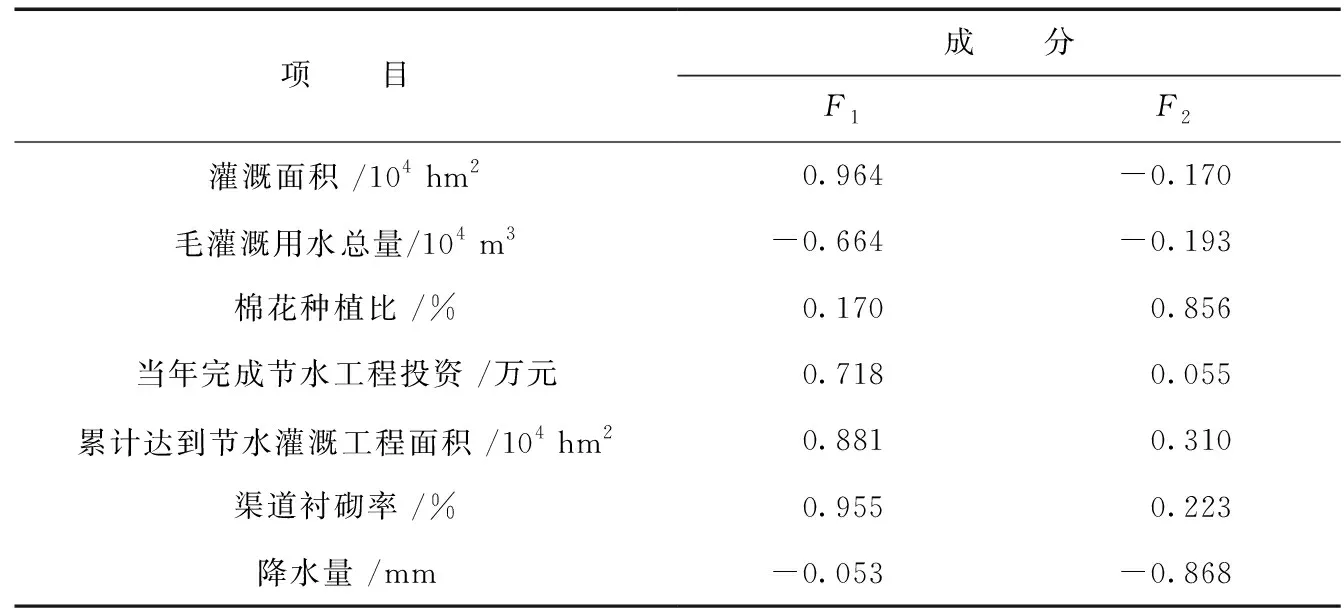
表9 旋转后的成分矩阵Tab.9 The component matrix after rotation

2.3 多元线性回归分析

2.3.1 分析计算过程

通过多元线性回归分析，建立以第一、第二主成分为自变量，以灌溉用水有效利用系数为因变量的多元线性回归模型。

2.3.2 分析结果

R2反映了通过变量能够对结果变量的方差变化做出多少比例的解释。模型中R是0.963，即模型中的自变量和应变量的相关性达到0.963。模型输出结果见表10。

表10 模型输出结果Tab.10 Model output

2.3.3 结果检验

Regression 回归部分的方差、Residual 残量部分的方差、Total 所有方差和的结果显示，本研究回归模型具有统计学意义，F(2，1)=44.082，P<0.05，表示因变量和自变量之间存在线性相关。P<0.05，说明多元线性回归模型中至少有一个自变量的系数不为零。同时，回归模型有统计学意义也说明相较于空模型，纳入自变量有助于预测因变量，或说明该模型优于空模型。

表11 方差分析表(F检验)Tab.11 Analysis of variance (F test)

通过表12可得，综合指标F1、F2的P值都小于0.05，说明F1、F2对灌水系数影响比较显著，可以保留F1、F2，模型合理，可以用于估测灌溉用水有效利用系数。

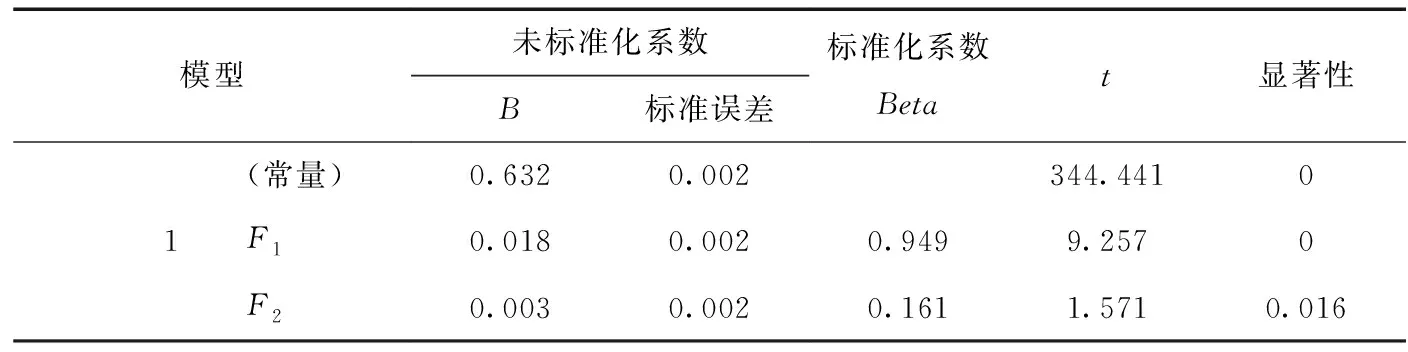
表12 系数输出表(T检验)Tab.12 Coefficient output table (T test)

综上所述，以第一、第二主成分为自变量，灌溉用水有效利用系数为因变量，建立的多元线性回归方程为：

Y=0.018XF1+0.003XF2+0.632

(4)

式中：因变量：灌溉用水有效利用系数Y；自变量：F1、F2分别为主成分分析得到的第一、第二主成分。

3 结 论

本文对自然因素、种植结构及管理因素、节水灌溉因素几大方向进行分析筛选，建立影响因素指标体系，采用Spss软件对影响因素进行主成分分析，将多个存在共线性的影响因素指标转化为两个相对独立的综合指标。通过验证分析这两个综合指标，可以很好地表达原始影响因素，然后以2个综合指标为自变量，以灌溉用水有效利用系数为因变量，建立多元线性回归分析模型。通过验证，该预测模型的可靠性较高，可以作为今后第八师灌溉用水有效利用系数的估测值。