基于人工神经网络的大坝变形监测研究
2021-09-27苏建伟
苏建伟
(黑龙江省水利水电勘测设计研究院,哈尔滨 150080)
0 引言
通过分析大坝的原型观测资料,建立大坝的安全监控模型,然后对大坝进行安全评价,不仅可以发现异常现象,及早推测大坝的未来状态和发展走势,阻止塌坝的发生,保护人民群众生命财产安全。还可以检验大坝设计的准确性,从而对设计、施工、管理的技术水平进一步提升,使各安全监测项目更加完善。
近年来,对大坝观测数据处理与分析方面的研究方法越来越多,有人工神经网络算法、模糊数学与神经网络方法的有机结合等等,为相关领域方面的研究都提供了可靠的保障。赵斌2008年通过对比模糊系统和神经网络的优缺点,建立了大坝安全监测的模糊神经网络算法的模型;何勇军2002年应用人工神经网络技术研究了大坝监测数据的分析方法,建立了基于自学习神经元的自学习即网络监控模型,为大坝安全监控模型的建立和预测开辟了新的前景[1];邓兴升、王新洲2005年[2]以东江大坝12个测点的变形历史水平位移为例,进行了模糊神经网络模型的建立,得出模糊神经网络模型的预报精度更高;闫滨学者,在大坝的安全监控预报和安全评价领域,研究了一种把BP神经网络和其他智能算法相融合的方法,从而建立起相应的智能神经网络模型,并取得了可观的效果[3-6]。
文章通过分析现有的大坝监测数据,运用神经网络算法来预报大坝未来的变形规律,并建立相应的神经网络模型,为未来大坝的安全评估和分析评价提供了一种有效的方法。
1 研究方法
人工神经网络是一种运算方法,它是由大量的神经元按照一定的连接模式互连构成的网络,包括输入层、影层和输出层三个部分,是基于模仿生物大脑的结构和功能而形成的一种计算机信息处理系统。
1.1 人工神经元模型

图1 单个人工神经元模型图
单个的神经元模型是由n个输入分量组成的,它包括三个部分:
1)一组连接(对应于神经元上的突触),各连接上的权值表示其连接强度,正值说明是激活,负值说明是抑制。
2)一个得到各输入信号加权和的求和单元。
3)一个非线性激活函数,它主要用于非线性映射,并限制神经元的输出幅度(一般限定在(0,1)或(-1,1)之间)。
此外还有一个偏差,即阈值θ[4]。
1.2 神经网络的学习
BP网络的学习过程分为两个阶段:
1)首先,键入己知的学习样本,先设置好网络结构,把前一次迭代的权值、阈值,从输入层经过隐含层,最后到达输出层,称之为前向传播。
2)其次,从输出层到隐含层,最后到输入层,依次调节隐含层到输出层的权重和偏置,输入层到隐含层的权重和偏置,称之为误差的反向传播。
以上两个过程反复交替,直到达到收敛为止。
2 基于人工神经网络算法的大坝变形数据分析
2.1 数据整理
采用的数据为位于四川省甘孜藏族自治州康定县境内的金康电站,该电站共有10个观测站点,本次选用的是位于首部枢纽闸坝引张线水平位移和竖直位移中的前5个站点,其中有大致分为三部分:
1)选取了20组其他站点的竖直位移数据作为自变量,而采取另一组竖直位移为因变量,观察其相邻站点及历史站点数据之间的关系;
2)选取了31组同一站点的水平位移和竖直位移数据,通过人工神经算法分析其两者之间的关系;
3)通过算法对历史数据进行预测,不断修正其精度,对未来数据进行预测。
通过近年来的数据比较,由于部分年限的数据缺失及波动较大,最后选取了07年一月份的竖直数据进行使用,然后对此数据进行归一化处理。数据的归一化处理目前采用较多的是将数据通过处理使其集中在[-1,1]之间,然后作此分析。其经验公式如下:
(1)
式中:X为原始数据;Xmax,Xmin分别为原始数据的最大值和最小值;T为变换后的数据,也称目标数据;Tmax,Tmin为目标数据的最大值和最小值,它们的取值通常为0.1-0.2和0.8-0.9。
2.2 训练参数的确定
训练参数包括输入组数、隐含节点数、训练次数、训练精度等参数的确定。
2.2.1 输入元组数的确定
由于所研究的是竖直位移的历史性和其邻近站点数据的关系,因此选取的数据包括其站点历史数据和临近站点数据。此次选取的数据为5号站点,采用1-4号站点为临测站点。经过多方查阅资料,最终选取历史数据为31,加上之前选择的临近站点的4个数据,所以其输入元为35。

表1 文章采用的部分垂直数据一览表 mm
2.2.2 隐含节点数的选择
Jc=(0.43mn+0.12n2+2.54m+0.77n+0.35)0.5+0.51(m为输入节点数,n为输出节点数)
由以上计算的隐含节点数Jc=6,由于试验发现这个并非最优隐含节点数,因此需要通过其他方法来确定最优隐含节点数。这里我们采用了‘0.618分割选取法’,具体步骤计算如下:
1)以Jc=6作为隐含层节点数的初始值
2)建立35-I-1的3层数值优化BP网络其中X=2kJc(k=0,1,..)。选取前1个月的位移数据作为学习样本进行训练,初始权值随机产生,设定训练目标精度为0.0001并对10次训练结果数据取平均值。找出误差下降最快的范围为[6,24],因此在[6,24]区间上采用0.618分割法寻找较优的隐含层节点数见表2。

表2 0.6l8分割结果
由以上算法得到Jc=20。
2.2.3 训练次数和精度
训练次数选为1000次,训练精度选为10-2。此次我把训练数据分成三个方面,训练网络、验证网络、测试网络。其中训练网络为70%,验证网络为15%,测试网络为15%。运行结果如图2、图3所示。

图2 训练参数一览表 图3 训练过程图
由上图显知输入单元为35组,而隐含节点数为20个,输出单元为1个。与原假定一致。
2.3 基于人工神经网络算法的大坝变形数据分析
采用matlabR2010神经网络工具箱进行计算,其误差分布图如图4所示。由图可知:误差分布均匀,除中间有些许误差除外,其余误差均可忽略不计,说明误差极小。
训练数据、输出数据与测试数据关系图如图5所示。

图4 误差分布矩阵图

图5 训练数据、输出数据和测试数据的关系
通过图5可以看出测试数据与理想数据拟合状况良好,而训练数据与验证数据误差较小,稳定在10-2之内,符合精度要求。因而可以认为此次训练过程运作良好,即竖直位移与其历史站点和临近站点相关性显著。
水平位移的计算方法与竖直位移的计算方法一样,计算结果也表明水平位移与其历史站点和临近站点相关性显著。进一步分析水平和竖直位移的关系时,将Jc值取为50,得到的运行结果为图6,误差为图7。

图6 验证数据、测试数据、训练数据和理想数据的拟合图
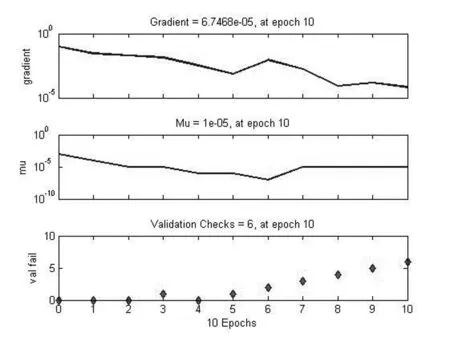
图7 均方差与梯度误差趋势图
由上述分析可得出以下结论:
1)坝体竖直位移间存在着紧密的关系,具体包括:坝体竖直位移的历史性关系,即在允许较小误差范围情况下,坝体的竖直位移随着时间的变化而呈现有规律的变化;临近站点间的位移变化存在着密切的关系,即各站点的位移对临近站点间的位移变化有着显著的影响。
2)水平位移与竖直位移间存在着显著的相关性,即水平位移对竖直位移的影响十分显著。
3 结 论
从大坝变形分析与预测的现状着手,通过对人工神经网络的介绍和学习,研究了BP 神经网络模型在大坝变形预测中的应用。其研究成果如下:在对人工神经网络介绍和学习的基础上,深入研究了BP 神经网络模型的结构和算法。通过人工神经网络算法在大坝变形监测方面的应用,更加明晰了大坝位移间的关系,也进一步加深了对人工神经网络的理解。
BP算法作为目前网络训练最常见的学习方法,经学者的研究表明它有着两个明显的劣处,即收敛的速度慢和可能会收敛到局部极小点。由于时间和个人知识水平的限制,仍有这两个问题有待于进一步研究和扩展。期望今后有机会可以另加深入研究,让这个方法更加成熟。取得更加广泛的应用。
