考虑电价弹性矩阵及波动风险的最优售电策略研究

逯景涛 王屹然

摘要：新一轮电力体制改革以来，售电商面临著市场价格和用户侧负荷双重波动的风险。因此，深入研究考虑风险特征的不同售电策略，从而制订最优售电策略，成为售电商面临的关键问题。现首先建立电量电价弹性矩阵，分析用户购电量与售电商出售电力价格的关系;其次考虑电价波动风险，建立以售电商收益最大化为目标函数的售电模型;最后针对在用户呈现出不同的电量电价弹性特征时售电商最优的售电策略进行了算例分析。

关键词：电量电价弹性矩阵;电价波动风险;售电策略

0    引言

随着电力市场改革的加快，售电侧市场正逐步开放，其中售电商因作为售电市场的主体而决定着市场活力。但是，在交易过程中，售电商既承担负荷预测的不精确和用户需求电量的实时波动的风险，又承担市场电价的波动性和不确定性的风险，来自购电侧和售电侧的双重波动风险使售电商难以保证自身收益。因而，考虑相关风险的售电策略成为售电商需要研究的关键问题之一。

关于售电商在市场交易中所面临的风险及其度量方法，文献[1]研究了购电电价和售电电价固定的供电公司在计及风险偏好的基础上对购售电策略的优化;文献[2]为降低购售电风险，提出了一种考虑需求弹性矩阵和风险规避因子的供电公司购售电优化决策模型;文献[3]基于条件风险价值法和实时电价机制，提出了一种考虑不同风险偏好的供电商的优化购售电组合决策模型。上述研究对用户购电量与电价的关系鲜有考虑，因此本文首先建立电量电价弹性矩阵，以此反映用户面对售电商出售电力价格的购电量;其次分析电价波动风险，将条件风险价值（CVaR）纳入售电商不同售电方案的收益之中，建立了售电商在不同用户之间的售电分配方案;最后，所提模型和方法的有效性可用算例来证明，为售电商的售电决策和风险评估提供了一条新的途径。

1    电量电价弹性矩阵

经济学的基本原理指出，建立价格机制是建立市场机制的主要任务之一。由此看来，为建立有秩序、可持续的电力市场，充分利用市场的杠杆作用来实现电价的调节尤为重要。用户对电价的响应是售电商应该考虑的重点，表现为用户需求对价格的敏感度，即用户的价格需求弹性。

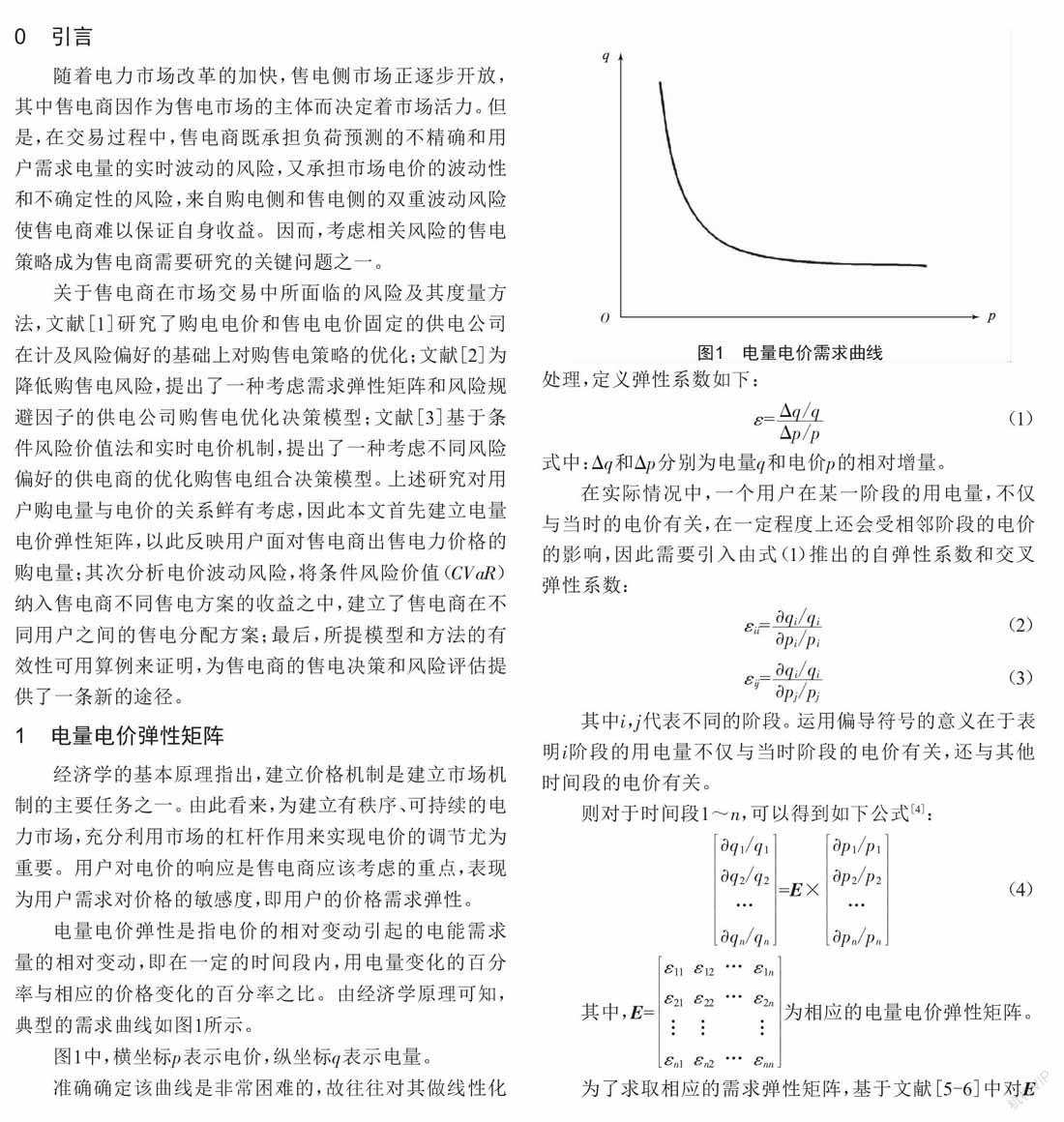
电量电价弹性是指电价的相对变动引起的电能需求量的相对变动，即在一定的时间段内，用电量变化的百分率与相应的价格变化的百分率之比。由经济学原理可知，典型的需求曲线如图1所示。

图1中，横坐标p表示电价，纵坐标q表示电量。

准确确定该曲线是非常困难的，故往往对其做线性化处理，定义弹性系数如下：

式中：Δq和Δp分别为电量q和电价p的相对增量。

在实际情况中，一个用户在某一阶段的用电量，不仅与当时的电价有关，在一定程度上还会受相邻阶段的电价的影响，因此需要引入由式（1）推出的自弹性系数和交叉弹性系数：

其中i，j代表不同的阶段。运用偏导符号的意义在于表明i阶段的用电量不仅与当时阶段的电价有关，还与其他时间段的电价有关。

则对于时间段1～n，可以得到如下公式[4]：

其中，E=ε11  ε12  …  ε1nε21  ε22  …  ε2εn1  εn2  …  εnn为相应的电量电价弹性矩阵。

为了求取相应的需求弹性矩阵，基于文献[5-6]中对E的特征分析，做出如下假设：

ε11=ε22=…=εnn=ε0，ε12=ε23=…=ε（n-1）n=ε1，ε13=ε24=…=ε（n-2）n=ε2，             …ε21=ε32=…=εn（n-1）=ε-1，ε31=ε42=…=εn（n-2）=ε-2，             …             （5）

该假设的含义为：对于任意给定的时间间隔l，任意时间段i的电价对时间段i+l的同一类电能消费具有相同的影响程度。此时，公式（4）可以简化为：

式中：pi+l为与i时间段相邻距离为l的该时间段的电价;εl为相应的弹性系数;m为对i时间段电量有影响的时刻范围。

因为整个时间段选为1～n，所以当i+l<1或者i+l>n时，取？鄣pi+l/pi+l=0。

2    售电商售电模型

售电商在不同的市场购买电能，并把它卖给不同的用户，从中获取差价利润。但是，在交易过程中，售电商面临着来自市场电价和负荷预测及用户需求电量的不准确性及波动，当波动比较大的时候，售电商就有可能面临负的收益，因此，风险已经成为售电商不得不考虑的问题。

2.1    考虑价格风险CVaR的计算方法

对于某一确定的售电方案，该方案下的售电商的损失可以表示为收益的相反数，数学表达式为：

式中：C为售电商购电成本;pi为售电商向用户i供应电力的价格;qi为向用户i供应的电量;K为用户个数。

此时：

式中：a为该购电组合在某一置信水平β下的最大可能损失，即VaR损失;m为所取历史数据或模拟样本的个数。

2.2    考虑价格风险CVaR的最优售电策略数学模型

售电商以最大化收益为目标，并将条件风险价值考虑进收益之中，其数学模型可以描述为：

式中：Q为售电商总购电量;qimin和qimax分别表示用户i最小用电量和最大用电量。

3    算例分析