一类递归型数据中心网络上容错单播算法的研究
2021-09-26伊雯雯张书奎李文俊
伊雯雯,张书奎,王 喜,,李文俊
1. 苏州工业职业技术学院 软件与服务外包学院,江苏 苏州 215004; 2. 苏州大学 计算机科学与技术学院,江苏 苏州 215006
近年来,随着云计算和大数据应用的飞速发展,数据中心网络(Data Center Network)作为其基础设施和下一代网络技术的创新平台,得到了学术界和工业界的广泛关注[1-3].
数据中心网络的容错性是评估网络性能的重要因素.连通度是度量数据中心网络容错性的一个重要参数,连通度越大,则数据中心网络的容错性能就相对越高.数据中心网络连通度定义中,发生故障的服务器是任意的、没有限制条件的,然而实际情况往往并非如此.仅使用连通度来评估数据中心网络的容错性,会严重低估数据中心网络的容错性能.因此,涌现了大量在特定网络拓扑上的限制连通度问题的研究成果[3-12].
传统的树型数据中心网络存在可扩展性不足和容错性较差等缺点,因此研究者们提出了DCell,BCube等多种递归型数据中心网络,与树型数据中心网络不同,这些结构采用递归方式构建网络拓扑,理论上可以支持百万台服务器的规模[13-14],且它们避免了核心层交换机带来的性能瓶颈,并使服务器之间拥有多条可用的不相交路径,其在可扩展性、容错性等多方面都有较好表现.本文提出了一类递归型数据中心网络——RDCN,与传统树形数据中心网络相比,该网络具有更好的网络带宽和网络容错性能;研究了递归型数据中心网络的限制连通度,该结果能够更加精确地度量该网络的容错性.本文将讨论RDCN在限制故障顶点集情形下的限制连通度,并设计和分析了相应的容错单播算法.
1 预备知识
数据中心网络可以表示为一个简单图G=(V(G),E(G)),其中V(G)表示顶点集,E(G)表示边集.顶点和边分别表示数据中心网络中的服务器和连接服务器的链路,而交换机被认为是透明的网络设备[13].给定图G中任意两个顶点u和v,若(u,v)∈E(G),则u和v是邻居.顶点u在图G的邻居集合可表示为N(G,u)={v|(u,v)∈E(G)}.图G的连通度可表示为κ(G).
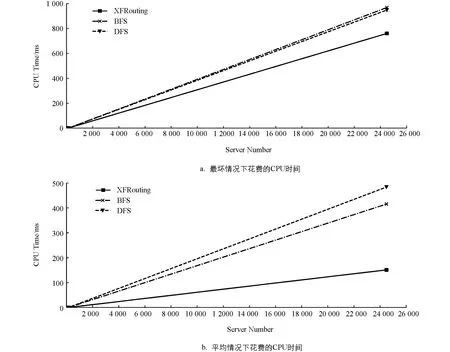
图G中两个顶点u和v之间的路径P可表示为一个顶点的序列P=(u0=u,u1,…,uk=v),P中除了u和v以外的任意两个点都是不同的.从ui到uj的子路径可用Path(P,ui,uj)表示,其中0≤i 进一步,对于顶点集合V′⊆V(G),定义V′的邻居集合为Γ(G,V′)=∪x∈V′Γ(G,x)/V′.明显地,Γ(G,V′)=N(G,V′)/V′. 定义1给定图G,令F⊂V(G)表示G中一个故障顶点集合,如果u∈F,那么u是G中一个故障顶点;否则,u是G中一个无故障顶点.若G中每个顶点至少有一个无故障邻居,则基于该条件下G的限制连通度可表示为κ′(G).另外,基于故障顶点无限制的G的连通度可表示为κ(G). 对于任意整数n≥3和k≥1,部署于n-口交换机上的k-维递归完全图网络可以表示为一个图Xk,n.Xk,n的基图是一个有n个顶点的完全图,tk,n表示Xk,n的顶点个数,e(u,v)表示顶点u到顶点v的边,σ表示图中任意顶点与同维度其他子图相连接的边数,其中σ∈{1,n-1},s表示Xk,n中子图的个数.Xk,n的顶点u表示为[uk,uk-1,…,ui,…,u0],其中0≤u0≤n-1,0≤ui≤si且i≥1,可用(u)i表示u中的第i个元素ui. 定义2当k≥0,n≥3且σ∈{1,n-1}时,Xk,n的递归定义如下: (1) 当k=0时,Xk,n是一个具有n个顶点的完全图. 根据文献[13]和文献[14],可得出Xk,n网络的基本性质如下. 定理1Xk,n是一个(n+kσ-1)-正则图. 定理2κ(Xk,n)=λ(Xk,n)=n+kσ-1. 本文将RDCN与几种典型的数据中心网络进行对比(如表1所示),其中N表示服务器数量,n表示交换机端口数量,比较的指标包括: 顶点的度、连通度和网络直径.其中数据中心网络中顶点的度越小则表示其顶点间网络连接越少,从而构建网络的成本越低;数据中心网络的连通度越高,则表示其具有更好的容错性;数据中心网络的直径越小则表示它的实时响应路由所花费的时间越少. 表1 几种常见数据中心网络性质比较 与RDCN相比,Tree和Fat-Tree的扩展规模在理论上受限于核心交换机的端口数目,不利于数据中心网络规模的快速扩张,且它们的容错性受到核心交换设备影响较大,对核心交换设备的故障非常敏感.同时,Tree和Fat-Tree的拓扑结构的特点决定了其不能很好支持一对多、广播和全交换等网络通信模式.另外,与RDCN相比,FiConn网络的容错性较差,网络直径较大.因此与上述数据中心网络相比,RDCN具有较高的网络带宽、较好的容错性.特别的,σ=n-1时的RDCN比σ=1时的RDCN具有更高的网络带宽和容错性能. 根据定义2,可以证明下述引理成立. 引理3[15]对于任意的整数k≥1,n≥3且σ∈{1,n-1},Xk,n上存在长度为3的圈. 引理4[15]对于任意的整数k≥1,n≥3,σ∈{1,n-1},Xk,n中存在相邻的两个顶点u=ukuk-1…u0和v=vkvk-1…v0,边(u,v)∈E(Xk,n),令leftIdx(u,v)表示为u和v从左侧开始最先不同的下标,则有 引理5对于任意的整数k≥1,n≥3且σ∈{1,n-1},网络中的故障顶点集合F⊂V(Xk,n)且|F|≤2kσ+n-3,若Xk,n中每个无故障顶点都至少存在一个无故障邻居,则Xk,n-F是连通的. 证要证明上述情况成立需要证明下述断言成立. 断言.对于任意两个不同的顶点u,v∈V(Xk,n-F),在Xk,n-F中存在一条连接u和v的路径. 当k=1时,该断言显然成立. 令α=(u)k,β=(v)k,当k>1时,可以分两种情形讨论. 1) 若fα≤n+kσ-3,则G0是连通的,因此G0中存在u和v的路径连接; 2) 若fα≥n+kσ-2,且u,v在同一个连通分支,则G0中存在u和v的连接路径; 3) 若fα≥n+kσ-2,且u,v不在同一个连通分支,假定x是u的一个无故障邻居顶点,y是v的一个无故障邻居顶点.令γ=(x)k且δ=(y)k,接下来可以分为以下3种子情形. 情形1.1α≠δ且α≠γ.对于任意整数i∈Ik,n{α},有fi≤|F|-fα≤(2kσ+n-3)-(n+kσ-2)=kσ-1≤n+kσ-3.根据引理2,G1是连通的,G1中存在路径Q连接x和y.因此Xk,n-F中存在路径(u,x,Q,y,v)连接u和v. 令 对c′求导则有 显然有min(c′)=n+2kσ-2.不失一般性,假设x1=u1,x2=u2,…,xc=uc,则有{uc+1,uc+2,…,un+kσ-3}∩{xc+1,xc+2,…,xn+kσ-3}=Ø. 因为|F|≤2kσ+n-3 和 根据情形1.1中讨论,G1中存在一条路径P连接z和y.因此,Xk,n-F中存在一条路径(Q,P,v)连接u和v. 情形1.3α=δ.证明与情形1.2类似,不再赘述. 若fα=n+kσ-2则fβ≤|F|-fα≤(2kσ+n-3)-(kσ+n-2)=kσ-1≤n+kσ-3,与fα≤fβ矛盾.因此fα≤n+kσ-3.接下来,分以下两种情形讨论. 根据引理2,可得G1是连通的,故G1中存在一条路径Q连接u和x.从而路径(Q,P-1)是Xk,n-F中连接u和v的一条路径. 综上所述,对于任意的u,v∈V(Xk,n-F)且u≠v,Xk,n-F中存在一条连接u和v的路径,因此Xk,n-F是连通的,证毕. 定理4对于任意整数k≥1,n≥3且σ∈{1,n-1},κ′(Xk,n)=2κ(Xk,n)-n=2kσ+n-2κ′(Xk,n)=2κ(Xk,n)-n=2kσ+n-2. 证通过引理5可得κ′(Xk,n)≥2kσ+n-2κ′(Xk,n)≥2kσ+n-2.下面将证明κ′(Xk,n)≤2kσ+n-2成立. 对于任意的整数k≥1,n≥3且σ∈{1,n-1},如果Xk,n中每个顶点都至少有一个无故障邻居,则存在一条边(u,v)∈E(Xk,n),使得|Γ(Xk,n,{u,v})|=2kσ+n-2且Xk,n-Γ(Xk,n,{u,v})有且仅有两个连通分支: 其中一个连通分支为Xk,n[{u,v}],另外一个连通分支为Xk,n-N(Xk,n[{u,v}]). 首先证明当n=3,k=1时该结论成立.当n=3,k=1时,分为两种情况:σ=1或σ=n-1. 当n=3,k=1,σ=1时,选择一条边(00,01),令故障集合为Γ(X1,3,{00,01})={02,10,20}.明显的|Γ(X1,3,{00,01})|=3=2×1×1+3-2.容易验证X1,3-Γ(X1,3,{00,01})有且仅有两个连通分支: 其中一个连通分支为X1,3[{00,01}],另外一个连通分支为X1,3-N(X1,3,{00,01}). 当n=3,k=1,σ=n-1时,选择一条边(00,01),令故障集合为Γ(X1,3,{00,01})={02,10,11,20,21}.明显的|Γ(X1,3,{00,01})|=5=2×1×(3-1)+3-2.容易验证X1,3-Γ(X1,3,{00,01})有且仅有两个连通分支: 其中一个连通分支为X1,3[{00,01}],另外一个连通分支为X1,3-N(X1,3,{00,01}). 通过上述过程知κ′(Xτ,n)≤2τσ+n-2成立. 综上所述,当n≥3,k≥1,σ∈{1,n-1}时,κ′(Xk,n)=2kσ+n-2,证毕. 定理4证明了递归型通用网络上限制连通度的精确值,本节将提出网络上基于限制故障顶点集合的单播算法XFRouting. Algorithm: XFRouting Input: A networkXk,n,a global variableσ∈{1,n-1},a faulty node setF⊂V(Xk,n) with |F|≤2kσ+n-3,and two nodesu,v∈V(Xk,n). Output: A path fromutov inXk,n-F. Letσto be a global variable; print (XFR(Xk,n,F,u,v)); function XFR(Xk,n,F,u,v,k) 1. if (u,v)∈E(Xk,n) ork=0 then 2. return (u,v); 3. else if |F|≥2kσ+n-2 then 4. return (BFS(Xk,n-F,u,v)); 5. else ifF=Ø then 6. ifσ=1 then 7. return DCellRouting (Xk,n,u,v); 8. else ifσ=n-1 9. then return BCubeRouting (Xk,n,u,v); 10. end if 11. end if 12. LetmFas the first index of the subsets with the minimal number of fault nodes 13. Letα←(u)k,β←(v)k; 14. ifα=βthen 16. else ifα∉mFthen 17. foriinmFthen 20. break; 21. end for 22. ifV(P)∩V(Q)=Ø then 24. end if 25. return (P,S,Q-1); 26. Find the 1st common nodexfromPandQ; 27. return (Path(P,u,x),Path(Q-1,x,v)); 28. end if 29. else ifα≠βthen 30. ifα∈mFthen 32. ifu∈V(Q) then return (Path(Q,u,v)); 33. end if 35. else ifβ∈mFthen 37. ifv∈V(P) then return (Path(P,u,v)); 38. end if 40. else then 41. foriinmFthen 44. break; 45. end for 46. ifV(P)∩V(Q)=Ø then 48. end if 49. return (P,S,Q-1); 50. Find the 1st nodexfromPandQ; 51. return (Path(P,u,x),Path(Q-1,x,v)); 52. end if 53. end function function XMapping(u,G0,G1,F,mF) 1. forvinN(G0-F,u) andvinmFthen return (u,v); 2. end for 3. forvinN(G0-F,u) then 4. forxinN(G1-F,v) andvinmFthen 5. return (u,v,x); 6. end for 7. end for 8. forvinN(G0-F,u) then 9. forxinN(G0-F,v) then 10. foryinN(G1-F,x) andyinmFthen 11. return (u,v,x,y); 12. end for 13. end for 14. end for 18. end function 接下来,定理5将给出XFRouting算法的设计思路和执行过程,并分析其时间复杂度. 定理5当k≥1,n≥3且σ∈{1,n-1}时,对于任意的顶点集合F⊂V(Xk,n)且|F|≤2kσ+n-3,算法XFRouting可以构造出Xk,n-F中任意两个不同顶点间的一条无故障路径,时间复杂度为O(k)≤O(┌logs|F|┐k3). 证当k≥1,n≥3且σ∈{1,n-1}时,故障集合F⊂V(Xk,n)且满足|F|≤2kσ+n-3,XFRouting算法可以构造出Xk,n-F中任意两个不同顶点u到v的一条无故障路径.XFRouting算法中包括4个函数: XFR,XMapping,DCellRouting[12]和BcubeRouting[13].其中实现函数XMapping构造出从G0中的顶点u到G1-F的一条无故障路径,函数DCellRouting构造出当σ=1时Xk,n中u到v的一条路径,函数BcubeRouting构造出当σ=n-1时Xk,n中u到v的一条路径.函数XFR将构造的路径以一个向量的形式保存,向量中的顶点采用长度为k+1的字符串表示. 函数XFR第1-2行,如果u和v存在边,则直接返回边(u,v).函数XFR第3-4行,如果条件满足|F|≥2kσ+n-2,则采用广度优先算法(BFS)构造一条无故障路径,在最坏情形下时间复杂度为O((tk,n)2).函数XFR第5-11行,当无故障顶点且σ=1时函数DCellRouting构造一条无故障路径,时间复杂度为O(k),当无故障顶点且σ=n-1时调用函数BcubeRouting构造一条无故障路径,时间复杂度为O(k).函数XFR第12行,计算最小故障子集,时间复杂度为O(k). 接下来分5种情况讨论函数XFR的时间复杂度,令R=n+kσ-1,mF表示故障数最小的子图前缀,s表示子集的个数,其中当σ=1时,s=tk-1,n+1,当σ=n-1时,s=n.函数XFR第14-15行,当α=β且α∈mF时,T(k)≤T(k-1)+O(R);函数XFR第16-28行,当α=β且α∉mF时,则有T(k)≤T(k-1)+O(R3);函数XFR第29-34行,当α≠β且α∈mF时,则有T(k)≤T(k-1)+O(R3);函数XFR第35-39行,当α≠β且β∈mF时,则有T(k)≤T(k-1)+O(R3);函数XFR第40-52行,当α≠β,α∉mF且β∉mF时则有T(k)≤T(k-1)+O(R3). 因此可得: 即O(k)≤O(logs|F|k3),证毕. 接下来,定理6分析XFRouting算法构造的路径长度的最大值. 定理6当k≥1,n≥3且σ∈{1,n-1}时,对于任意的顶点集合F⊂V(Xk,n)且|F|≤2kσ+n-3,XFRouting算法可以构造出Xk,n-F中任意两个不同顶点间的一条无故障路径,其路径长度的上界为 证令L(k)表示XFRouting算法构造得到的路径的长度.当|F|=0时,令D(Xk,n)表示图Xk,n的直径,根据文献[12]和文献[13],则有 当0<|F|≤2kσ+n-3时,分为以下情形讨论: 函数XFR第14-15行,L(k)=L(k-1);函数XFR第16-28行,L(k)≤L(k-1)+6;函数XFR第29-34行,L(k)≤L(k-1)+3;函数XFR第35-39行,L(k)≤L(k-1)+3;函数XFR第40-52行,L(k)≤L(k-1)+6. 令 d=logs|F| 则有 当σ=1时s=tk-1,n+1≫|F|,则d=logs|F|<1.因此有 证毕. 综上所述,本文提出的时间复杂度为O(logs|F|k3)的算法XFR与采用时间复杂度为O((tk,n)2)的广度优先搜索算法相比,具有明显的优越性. 本文提出的XFRouting算法采用Python语言编程实现,实验通过设备配置为Intel(R) Core(TM) i5-4200U CPU 1.61GHz,8 GB 内存的计算机来评估算法的性能并分析实验结果.实验中顶点故障和测试点都是随机生成的.给定随机生成的限制故障集合F⊂V(Xk,n)且|F|≤2kσ+n-3,给定σ=1,1≤k≤3,n=3,网络最大规模为24 492个顶点,将使用XFRouting算法构造出Xk,n-F上一条单播路径花费的CPU时间分别与广度优先BFS算法和深度优先DFS算法所得的结果进行比较.将XFRouting算法和BFS算法、DFS算法重复运行1 000次,随机生成故障顶点集合,构建任意两个顶点之间的无故障路径,最坏情况如图1(a)所示,平均情况如图1(b)所示. 图1 σ=1时3种算法花费的CPU时间 给定随机生成的限制故障集合F⊂V(Xk,n)且|F|≤2kσ+n-3,给定σ=n-1时,1≤k≤7,n=3,网络最大规模为6 561个顶点.将XFRouting算法构造出Xk,n-F上一条单播路径花费的CPU时间分别与BFS算法、DFS算法进行比较.将XFRouting算法、BFS算法和DFS算法重复运行1 000次,随机生成故障顶点集合,构建任意两个顶点之间的无故障路径,最坏情况如图2(a)所示,平均情况如图2(b)所示. 图2 σ=n-1时3种算法花费的CPU时间 根据实验结果,构造Xk,n-F上两个顶点间的一条单播路径所花费的CPU时间随着维度k的增加逐步增多.根据实验结果,当σ=1,n=3且k=3时,XFRouting算法、BFS算法和DFS算法所花费的最坏CPU时间分别为760 ms,960 ms和948 ms,平均CPU时间分别为151 ms,415 ms和483 ms;当σ=n-1,n=3且k=7时,XFRouting算法、BFS算法和DFS算法所花费的最坏CPU时间分别为234 ms,972 ms和990 ms,平均CPU时间分别为189.2 ms,362.6 ms和564.7 ms.由实验数据可以得到,本文所提出的XFRouting算法在执行效率上优于广度优先搜索算法BFS和深度优先搜索算法DFS. 数据中心网络的容错性是评估其网络性能的重要因素,如果用连通度来评估其容错性能,会低估数据中心网络的容错性能.基于每个顶点都至少有一个无故障邻居这一条件下的限制连通度,能够更加精确地度量数据中心网络的容错性.本文提出了一类递归型数据中心网络(RDCN),与传统树形数据中心网络相比,该网络具有更好的网络带宽和网络容错性能.证明了当k≥1,n≥3且σ∈{1,n-1}时,其限制连通度为2kσ+n-2,这一结果近于其连通度的2倍;接着提出了该情形下时间复杂度为O(「logs|F|⎤k3)的容错单播路由算法,证明了在最坏情况下构造出容错单播路由最长路径长度的上界.仿真实验结果表明XFRouting算法在执行效率上优于广度优先搜索算法和深度优先搜索算法.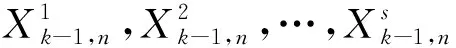
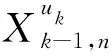
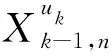
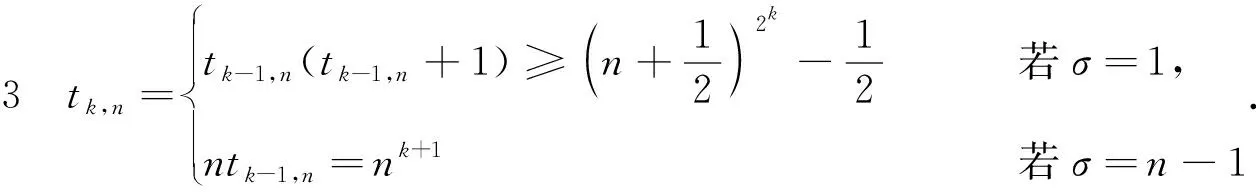

2 递归型数据中心网络的限制连通度
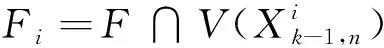
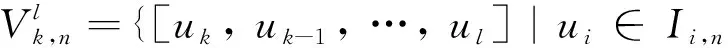
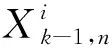
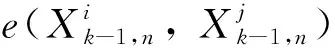



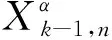

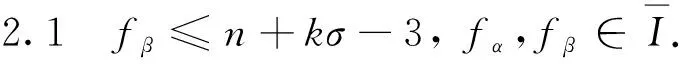
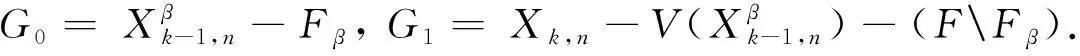
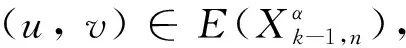
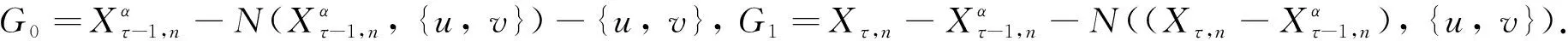
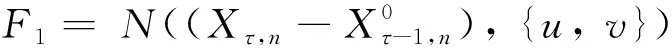
3 递归型数据中心网络基于限制故障集的单播算法
4 模拟实验及结果分析

5 结 论
