高速冲床床身模态分析与频率可靠性评估*

陈 浩

（常州纺织服装职业技术学院机电学院， 江苏常州 213164）

0 引言

作为一种高效的锻压设备，高速冲床在航空航天、汽车制造、交通运输、冶金化工等重要工业领域得到了广泛应用。尤其是近年来，以汽车为龙头的制造业的飞速发展，大大推动了我国冲压产业的进步。随着市场全球化步伐的加快，竞争越来越激烈；与此同时，用户对高速冲床的冲压速度和可靠性水平提出了更高的要求。在正常运行时高速冲床的冲压速度要远高于普通冲床，整机的振动也将远大与普通冲床。

近年来高速冲床的速度也不断提高，随着冲压速度的提升，整机的振动频率愈来愈高、幅度越来越大。高速冲床主要受到周期性的冲击载荷和电机转动的激励载荷[1-2]，在这两种外部激励载荷的作用下高速冲床会产生振动。若高速冲床所受外界激励载荷的频率接近于系统的固有频率时，则出现共振现象，共振会严重影响生产加工的正常进行。因此，有必要对高速冲床床身进行模态分析与频率可靠性评估[3-5]。对于提高机床的加工精度、延长使用寿命和降低噪声有着重要意义[6-7]。

为了避免高速冲床工作时产生共振失效，本文以某型高速冲床床身为对象，首先讨论了模态分析原理，然后建立床身的有限元模型，并进行了模态求解，得到了床身前4阶的固有频率与振型；最后，结合机械结构系统发生共振的准失效状态、失效概率的定义及其频率可靠度的计算方法，对其进行振动频率可靠性评估，评估结果显示该床身符合设计要求，不会出现共振问题；并且在此基础之上提出了避免高速冲床出现共振的措施。

1 高速冲床床身模态分析

1.1 模态分析原理

在结构动力学问题中结构固有频率和固有振型是动力学问题的研究基础，也是避免结构出现共振的关键。因此，为了获取上述信息，通常会对研究对象进行模态分析。模态分析原理如下。

一个多自由度的结构系统的动力学方程可描述为[8-9]：

式中：、、x分别表示加速度、速度、位移；F为载荷向量；M为质量矩阵；C为阻尼矩阵；K为刚度矩阵。

相比刚度来说，有些研究对象结构的阻尼较小，例如本文研究对象高速冲床床身。因此，有时候可忽略阻尼影响。

当外部载荷为0，可以得到无阻尼自由振动的运动方程：

其对应的特征方程为

式中：ω为固有频率。

由式（3）可求得固有频率为：

1.2 模态分析

基于上述模态分析原理确定研究对象模态特性的方法有2种：试验法和仿真法。

（1）试验法：通常采用力锤敲击研究对象，并采用加速度传感器在各个点位采集振动信号；然后，将加速度传感器信号和力锤信号经过电荷放大器方法后被数据采集装置所采集并保存；最后，采用数据分析软件对所采集的数据进行模态分析，获取其模态信息。

（2）仿真法：首先，采用三维建模软件建立对象的三维模型，在此基础上进行网格划分建立有限元模型，并设置材料属性与边界条件；然后，采用模态求解器进行模态求解；最后，进行后处理输出分析结果。在实际的工程应用中，由于模态试验需要测试的点较多，工作量较大、试验成本也较高，因此通常采用仿真法来获取研究对象的模态信息，所以本文也将采用此方法。

本文研究对象为某型高速精密冲床床身，该床身主要分为3个部分，分别为上梁、立柱和底座。上梁与立柱、立柱与底座之间均采用螺栓连接，该机床床身三维模型如图1所示。坐标如图1的左下角，左右方向为X轴、竖直方向为Y轴、前后方向为Z轴。床身左右长为2150 mm，前后宽为1250 mm，上下高为2800 mm，总质量为11602 kg。为了提高计算速度，对三维模型进行了必要的简化，忽略尺寸较小的特征，如倒角、圆角、小孔、小的沟槽等，同时也去除了连接的螺栓。简化后通过有限元软件建立床身的有限元模型，如图2所示。该模型采用四面体实体单元，共得到单元数318500，节点数为486352。由于该床身的3 个部分之间采用的是螺栓连接，本模型将其看做一个整体，进行了刚性连接处理。设置床身材料参数：弹性模量2.08×105MPa，泊松比为0.3，材料密度为7850 kg/m3。

图1 高速冲床床身三维模型

图2 高速冲床床身有限元模型

基于有限元分析软件对所建立的床身模型进行模态求解，获得了前4阶固有频率和振型特点如表1所示。由表可知该床身的前4 阶的固有频率分别为111.70 Hz、167.34 Hz、255.68 Hz和278.33 Hz。

表1 高速冲床床身固有频率与振型特点

床身前4阶的振型如图3所示。由图可知，第1阶振型为床身整体绕Y轴转动，上梁的扭动幅度大于立柱和底座的振动幅度，扭动幅度最小点在立柱的中下部；第2阶振型为床身上部沿X轴方向摆动，同样是上梁的振动幅度最大，立柱次之，底座最小；第3阶振型为床身上部沿Z轴方向摆动，同样是上梁的振动幅度最大，立柱次之，底座最小；第4阶振型为床身上部沿Z轴方向摆动，伴随轴承座部位沿Z轴方向大幅度摆动，轴承座部位的振幅要大于横梁的振幅。综上所述该床身的前4阶振型都是沿Y轴方向的扭动或沿X轴、Z轴方向的摆动。该型冲床是通过主滑块上下运动完成冲压作业的，因此敏感方向为Y轴方向，换句话说Y轴方向的振动对该高速冲床的精度影响最大，从前4阶振型来看，没有该方向的摆动，因此从该角度来看前4阶振型对该冲床精度影响较小。

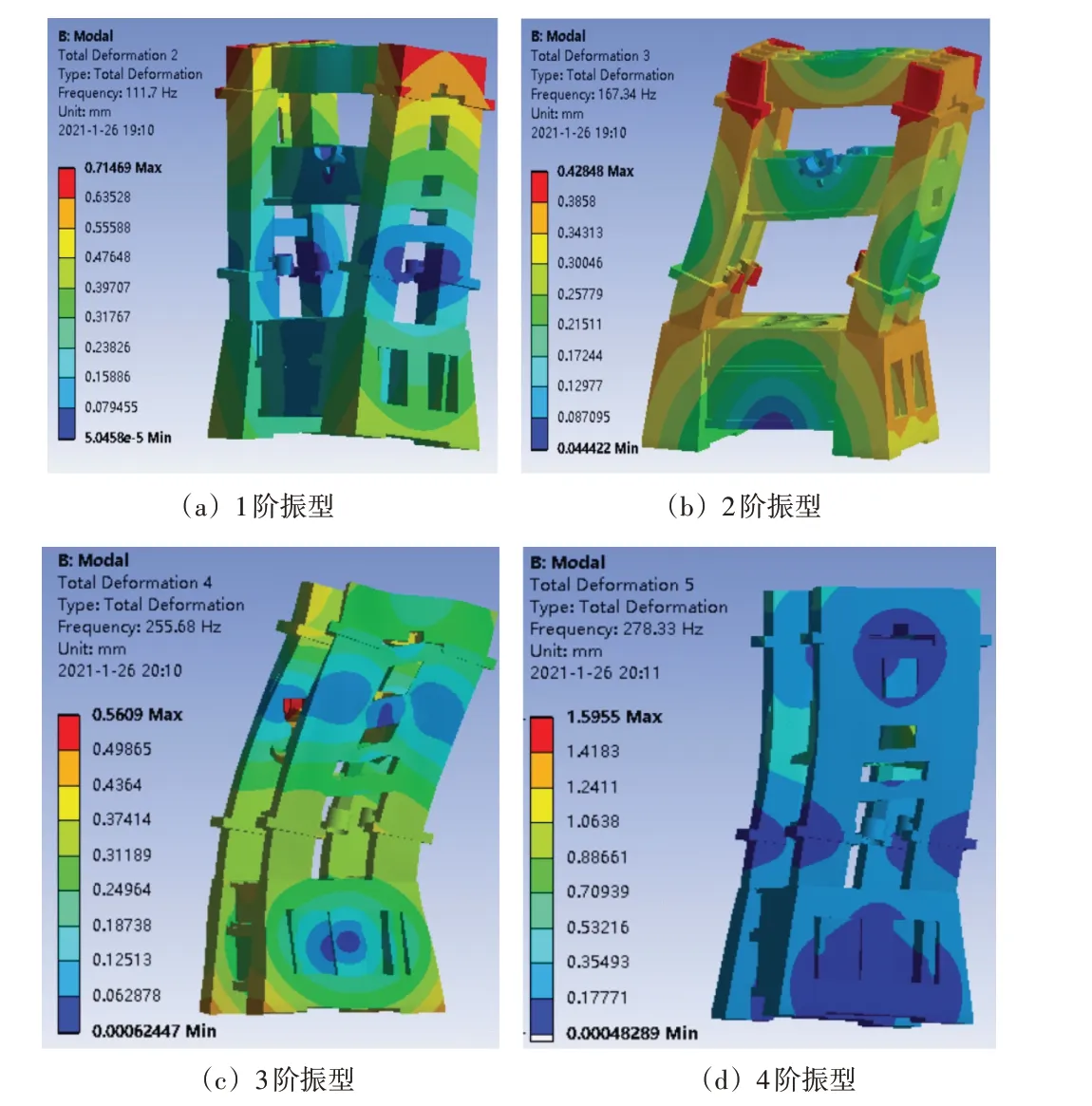
图3 高速冲床床身前4阶振型

2 频率可靠性评估

2.1 频率可靠性评估方法

频率可靠性反映的是结构不出现共振的概率，而结构出现共振的条件是外部激励载荷的频率与结构的固有频率之间重合或接近。根据可靠性分析的干涉理论，结构系统发生共振失效的状态函数可以表示为[10-11]：

式中：p为外部激励载荷第j个激振频率；ωi为结构系统的第i阶固有频率。

根据pj与ωi的关系准则，可确定结构系统发生共振的准失效状态函数为：

式中：γi为结构系统的第i阶固有频率的特定区间，根据工程经验γi一般取值为对应固有频率的0.1～0.15倍。

令gij=Pj-ωi，结构系统产生共振的概率，即准失效概率可以表示为：

在结构系统中，只要有一个激振频率与固有频率重合或接近，即会使整个系统处于共振状态。因此从共振失效的角度来看，结构系统应为一个串联系统，系统的频率可靠度可以表示为

机械系统受外界激振力的作用，取γi为相应固有频率的0.15倍，以频率为度量的系统可靠区间d，如图4所示。由图可知，系统频率可靠区的范围为1.15ωk～0.85ωk+1，换句话说外部激励载荷的频率在此范围内该机械系统不会出现共振问题。

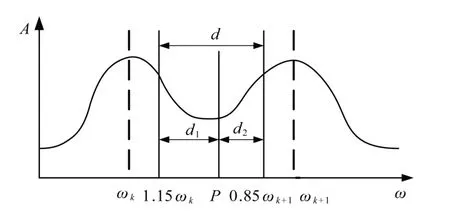
图4 频率可靠区间

2.2 频率可靠性评估

本文研究对象为某型闭式双点高速冲床的床身，该机床的主滑块行程次数为200～1200次/min；因此，在正常工作情况下高速冲床冲压激振频率范围为3.3～20.0 Hz，即冲压力的激振频率为P1=3.3～20.0 Hz。该型号高速冲床电机转速范围为460～3564 r/min（电机的额定转速为2970 r/min，可以通过变频器超频达到3564 r/min），其转动频率范围为9.8～59.4 Hz，即电机对机身的激振频率为P2=9.8～59.4 Hz。由模态分析可得该高速冲床固有频率为ω1=111.70 Hz、ω2=167.34 Hz、ω3=255.68 Hz、ω4=278.33 Hz。由于激励频率Max[P]＜ω1，所以取γ=0.15ω1，由式（7）～（8）可求得该高速冲床的频率可靠度为R=1，即在正常工作状态下该型高速冲床床身不会出现共振现象。因此，该型号的高速冲床满足频率可靠性设计要求。

根据频率可靠性理论提出避免高速冲床出现共振、提高频率可靠性水平可采取的方法如下：（1）优化高速冲床机身结构，使其固有频率与激振频率有一定的差值，且差值应大于对应固有频率的0.1～0.15 倍；（2）合理设计滑块行程次数，并在频率可靠区间范围内选择电机，使激振频率避开高速冲床床身的固有频率。

3 结束语

为了掌握高速冲床的模态特性及其频率可靠性，本文进行了模态分析，获得了某型高速冲床的前4阶的固有频率与振型。并在模态分析的基础上，对其进行频率可靠性分析。结果表明，在正常的工作条件下，外部激励频率、工作载荷频率和电机转动频率都小于高速冲床的第1阶固有频率，经过频率可靠性计算得到高速冲床的频率可靠度为1，即在正常工作这状态下床身不会出现共振现象。因此，从共振角度来看该床身满足设计要求。并在此基础之上提出了避免高速冲床出现共振的措施，对高速冲床设计中如何避免在工作频率范围内共振现象的产生有实际意义。