数学模型在工程测量中的应用

苗高攀 李忠朋

（河南思拓力测绘科技有限公司，河南 郑州 450000）

1 引言

2 方程拟合

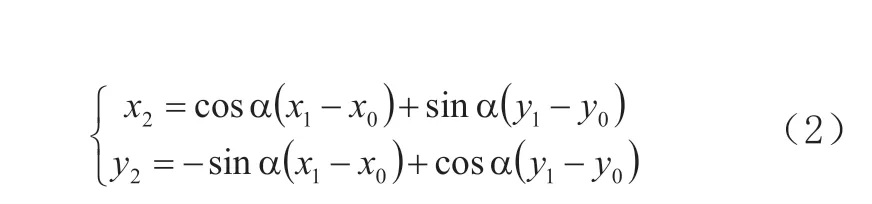
其中，x1、y1是地面辅助坐标系坐标，x2、y2是数学坐标系的坐标，x0、y0是两个坐标系的平移参数，α是两个坐标系之间的旋转参数。

得到放样点的地面辅助坐标系坐标后，需要通过常规测量手段获取地面辅助坐标系原点坐标，得到地面辅助坐标系与大地坐标系之间的旋转参数和平移参数，将放样点坐标归算到大地坐标系下。

2.1 螺线方程拟合

2.2 椭圆方程拟合

2.3 二维振动方程拟合

3 风速改正

表1 给出风力等级与风速的关系，当风力等级≥2时应进行风速改正，当风力等级≥8 时应停止观测，竖直方向的位置偏差过大，模型失效。

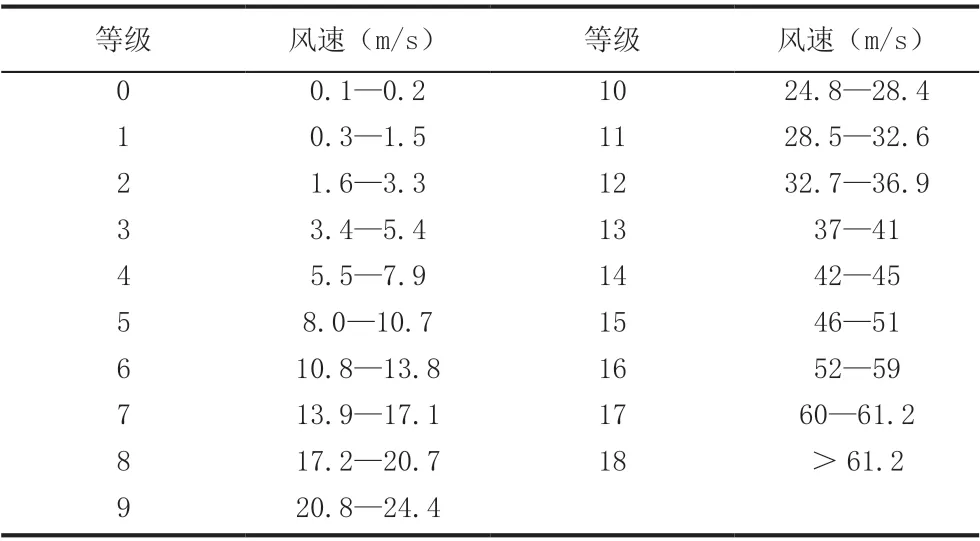
表1 风力等级表

4 结语

在三个拟合方法中，二维振动方程拟合最为精准，使用了物理分析，依托大量离散点数据，观测周期较长，计算量较大，效果最好，适用于高精度需求的工程 ；椭圆方程拟合计算量最小，观测周期最短，方法简单，但精度有限。螺线方程拟合保证了较高的精度和较高的效率，适用于大多数情况。

进行风速改正时应注意：（1）应当在风速稳定时进行计算；（2）重垂的形状应尽量规则，以便计算重垂的受力面积；（3）方程拟合的测量结果可直接加上风速改正量得到最终结果。

与传统悬线放样法相比，改进方法使用了数学拟合，具有逻辑性，可以使用传感器和计算机进行观测和计算，大大提高了工作效率和测量精度。计算机和传感器在工程测量领域的应用愈加广泛，依托数学、物理、计算机、传感器等工具支持的综合测量模型将逐渐代替部分传统工程测量方法，并取得更高的效率和精度。