基于WFT的直驱式波浪能发电系统自抗扰功率优化控制

黄俊豪，杨俊华，蔡浩然，林巧梅

（1.广东工业大学 自动化学院，广东 广州 510006；2.广州市市政工程设计研究总院有限公司，广东 广州510000；3.惠州工程职业学院 智能工程系，广东 惠州 516023）

0 引言

海洋波浪能具有清洁无污染、储量丰富、能量密度高等优点。据统计，海洋波浪能每年能够提供的电能超过2 TW，可满足目前全球的用电需求，所以波浪能发电技术发展潜力巨大[1]，[2]。

永磁直驱波浪能发电系统通过振荡浮子吸收波浪能，然后直接驱动电机将波浪能转换为电能，由于整个发电过程无机械传动装置，所以波浪能的转换效率较高[3]。提高波浪能捕获效率是波浪能发电的关键技术，当振荡浮子的运动速度和频率同外界波浪力的运动方向和频率一致时，振荡浮子和波浪会发生共振，此时波浪能捕获率和系统输出功率值最大[4]。

直驱式波浪能发电系统中的直线电机具有强耦合和强非线性的特点，电力电子器件会引起电流畸变及谐波分量，再加上输入海浪周期长和随机性强的特点，导致传统PID控制策略无法精确跟踪最大功率曲线[5]。根据振动浮子共振条件，文献[6]提出了阻尼力和刚度力的概念，通过分解q轴电流，结合PID控制器控制阻尼力与刚度力，并通过大电容平滑海浪不规则波动与噪音引起的功率波动，但该方案的电流分解过程繁复，实际应用操作难度大。通过对控制对象施加扰动，对比寻优，扰动观测法能有效提高波浪能捕获效率，优化发电系统的功率输出[7]，[8]。但是，输入波浪的随机性使扰动观测法在寻优过程中易陷入局部最优，无法捕获最大功率，且输入波浪周期长，噪音环境又会造成控制算法反应过强，引起无方向抖动，导致控制步长值的确定难度加大。波浪能发电系统存在许多不确定扰动，难以建立精确数学模型，滑模控制方案通过建立近似数学模型，选取合适滑模面，能有效抑制扰动对被控对象的影响，但须采用其他方案优化滑模控制的抖振问题[9]。

在电机控制中，相较于传统PID控制，自抗扰控制策略能快速响应电流指令，实现无超调跟踪，有效抑制外界输入突变与电压波动的影响[10]。风力发电系统中的外界风速测量噪点多，难以准确建模，文献[11]，[12]将自抗扰控制器应用于风力发电功率解耦控制，降低了对系统精确数学模型的依赖，解决了不可测量状态量的干扰问题。低通滤波器虽然可以滤去噪音，但过渡带较长，易出现失真现象，而输入波浪周期长，运动速度低，滤波效果不稳定。自抗扰策略中的跟踪微分器与扩张观测器滤波效果好，没有过渡带，能无噪音跟踪信号，可尝试用于波浪能发电系统稳定控制[13]。

除了控制策略，波浪能发电功率优化的另一个关键技术为波浪频率的检测预估。文献[14]提出了自适应矢量控制方案，利用锁频环预估不规则输入波浪的主频率，根据测速度设备监测到的波浪速度，自适应更新最优频率控制参数，形成完整波浪能量转换链，并通过直流母线相链接，减少系统功率振荡，但锁频环的工作依赖于基准频率，因此，只能依据历史数据选取基准频率。文献[15]提出了无速度传感器控制方案，对不规则激励力进行傅里叶分析与矢量叠加，并使用卡尔曼观测器滤除噪音的影响。将波浪信号通过傅里叶变换离散化是获取波浪主频段的有效手段，但傅里叶变换计算繁复，且对短时时域信号的离散效果不佳。

目前，大部分功率优化控制方案仅针对某一特定频率下的理想正弦波浪，将其应用于不规则波浪时，捕获效率较低，电流误差较大。为此，本文提出基于加窗傅里叶变换（Windowed Fourier Transform，WFT）的自抗扰控制方案，对不规则波浪激励输入进行加窗傅里叶分析，获取激励频谱，以提高分析速度及精度。结合矢量控制，设计电流自抗扰控制方案，减少由于不规则输入波浪与电力电子器件动作引起的纹波干扰，保证对电流期望值的跟踪精度，抑制超调量，从而实现波浪能发电系统的最大功率跟踪控制。

1 直驱式波浪能发电系统功率跟踪策略

图1为直驱式波浪能发电装置的结构及等效模型图。从图1可以看出，发电机动子与浮子相耦合，随波浪作垂直方向的直线运动，切割磁场产生电能。

图1 直驱式波浪能发电装置结构图Fig.1 The structure of direct-drive wave power converter

1.1 浮子动力学模型分析

根据牛顿第二定律，分析振荡浮子受力，可得波浪能发电系统的动力学方程:

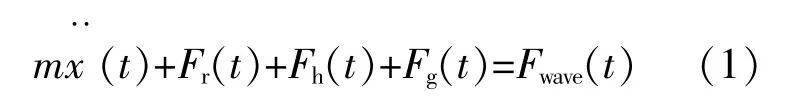
式 中:m为 发 电 机 动 子 质 量，kg；x（t）为 动 子 运 动位 移，m；Fr（t）为 运 动 浮 子 所 受 辐 射 力，N；Fh（t）为浮 子 所 受 静 浮 力，N；Fg（t）为 发 电 机 反 电 磁 力，N；Fwave（t）为 浮 子 所 受 到 的 波 浪 入 射 力，N。

浮子所受辐射力跟浮子运动速度和加速度相关，可表示为

式中:mf为浮子受到波浪力而产生的附加质量，kg；β为电机动子运动的附加阻尼系数，kg/s2。

浮子处于平衡位置时，所受静浮力可表示为

式 中:ρ为 海 水 密 度，kg/m3；g为 重 力 加 速 度，m/s2；S为浮子垂直方向浸没部分的面积，m2。

发电机反电磁力可表示为

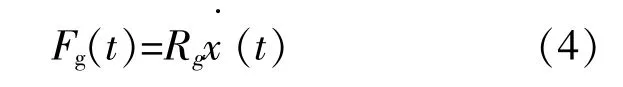
其中:Rg为波浪转换装置的阻尼系数（表征系统发 出 的 有 功 功 率），kg/s2。

令M=m+mf，则 式（1）可 以 简 化 为

观察式（5），发现其为二阶微分方程，与RLC电路方程具有相似性，于是作等效电路处理，得到图2所示的等效电路。

图2 等效电路图Fig.2 Equivalent circuit

由电路原理可知，当电路发生串联谐振时，输出能量值达到最大。共振频率 ω0为

忽略电机内部损耗，则等效电阻Rg上所消耗功率即为发电机所发瞬时有功功率P，P的计算式为

上式经过处理可得:

由式（8）可知，在共振频率 ω0下，波浪能发电系统输出最大功率的条件为

1.2 波浪能发电系统功率方程

忽略磁路饱和现象与磁滞、涡流损耗，永磁直线电机的数学模型为

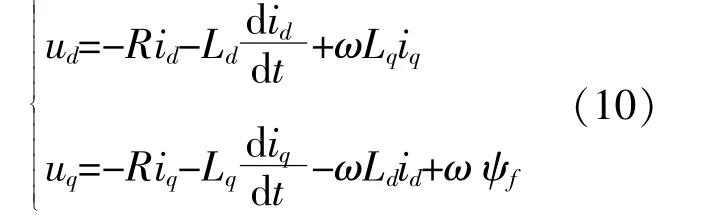
式中:R为电机定子电阻，Ω；id和iq分别为定子d，q轴 电 流，A；Ld和Lq分 别 为 定 子d，q轴 电 感，H；ud和uq分 别 为 定 子d，q轴 电 压，V；ω为 定 子电 气 角 速 度，rad/s；ψf为 永 磁 体 磁 链，Wb。

电机的反电磁力也可表示为

式中:τ为极距，m；p为极对数。

由式（8）可知，电机反电磁力与d，q轴电流相关。根据磁场定向控制策略，为减少电机损耗，提高输出功率，令

于是式（11）可以简化为

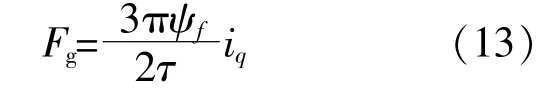
电机输出电磁功率P的计算式为

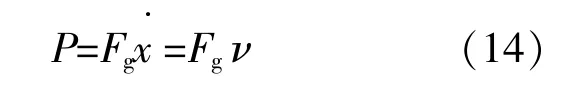
式中:v为电机动子的运动速度，m/s。

联 立 式（4），（13），可 得q轴 电 流 期 望 值:

由此可见，控制q轴电流，可控制电机输出功率，从而实现最大功率跟踪。

1.3 加窗傅里叶频谱分析

为保证波浪能发电系统输出最大功率，须要知道入射波浪激励力的运动频率，求解保证共振状态的等效电阻值，但实际海况中的波浪是长周期随机入射波，无法处理为理想规则波。傅里叶变换可以将时域上的信号转化为频域上的离散信号。入射波浪可以视作无穷多个周期和幅值不同的正余弦函数叠加而成的充满扰动的不规则波，因此，对入射波浪作傅里叶变换处理，可以得到入射频率谱，分析提取主要激励力频率，从而获得不规则入射波下的最大功率捕获条件。

受处理能力的限制，计算机对于无限长的信号只能提取局部信号，通过周期拓延的方式将该局部信号扩展为无限长的信号，然后再进行傅里叶变换。傅里叶变换在处理有限时长的时域信号数据时计算速度慢，且无法对局部特定频率信号进行有效处理，产生栅栏效应，且截取数据的窗效应使得信号畸变，出现频谱泄漏现象。为解决上述问题，通常根据输入信号的特点来选择添加的窗函数。加窗傅里叶变换对短时时域信号添加一个可以随时间轴移动的窗函数，并对窗函数范围内的信号进行傅里叶变换。由于波浪输入充满随机性与输入噪音，因此选用主瓣窄，抗扰能力较强的Hanning窗函数，其表达式为

式中:k为Hanning窗函数阶数。

对波浪入射力Fwave进行加窗傅里叶分解，得到多个不同运动频率下的正弦波输入:

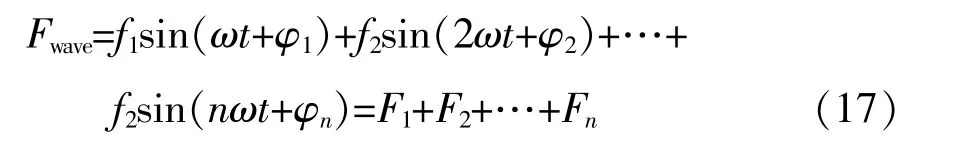
式 中:n为 谐 波 次 数，n=1，2，3...。

结 合 式（5）和 式（17），可 得:

根据叠加定理，傅里叶分解后可得到不规则波浪激励下对应最大功率捕获条件时的电磁力:

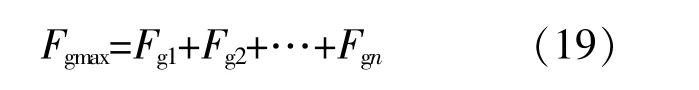
不同频率的激励输入，对应不同的反电磁力及谐振等效电阻值，依据式（15），可获得不规则波浪激励输入下的电流控制目标值。

2 自抗扰控制器设计

图3为自抗扰控制框图。从图3可以看出，自抗扰控制器由跟踪微分器 （TD）、扩张观测器（ESO）及 非 线 性 反 馈 律（NLSEF）构 成。

图3 自抗扰控制框图Fig.3 The control structure of ADRC

跟踪微分器对所采集输入信号进行过渡，提取有效微分信号，改善观测效果与系统稳定性。令d轴电流期望值为idref，d轴电流跟踪微分器为

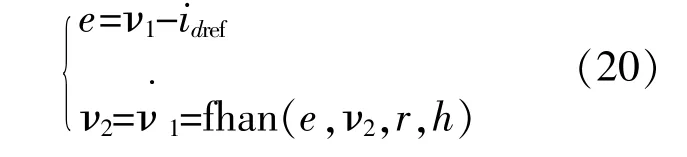
式中:r为速度影响因子；h为滤波影响因子；fhan为最速综合函数。

通过设计合适的综合函数可保证过渡微分效果，设计fhan函数为

系统未知干扰输入虽无法实时测量，但扩张观测器可观测非线性系统中的所有状态变量，并将不确定扰动量扩张为新的观测状态量，跟踪观测进行实时估计。扩张观测器不依赖扰动的数学模型，基于非线性约束反馈，构建n+1阶观测器，有效滤除扰动影响。

建立d轴电流扩张观测器:

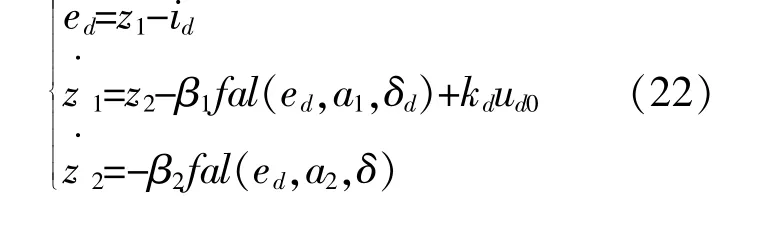
式中:z1为被观测系统输出的跟踪信号；z2为状态估计值；β1和 β2均为观测器校正系数；kd为控制系数；ud0为d轴非线性反馈补偿输入；fal为非线性结构函数，可依据误差修改反馈环节增益，提高系统稳定速度，是扩张观测器具有滤波功能的保证。

fal函数为

式中:a为0～1内的常数；δ为滤波因子，可表征线性区间宽度，依实际误差而定。

非线性反馈律是将跟踪微分器与扩张观测器串组起来的部分，根据微分器的跟踪反馈输出与扩张观测器观测状态量进行误差补偿，使系统能跟踪目标期望值，提高稳定性。

d轴电流非线性反馈律形式为

其中:β3为观测器校正系数；b为补偿系数。

至此，d轴电流自抗扰控制器设计完毕，同理可获得q轴电流自抗扰控制器。自抗扰控制器将非线性系统转换为积分串联补偿形式，无须准确获取输入噪音信号，也可实时预估状态量信息，实现误差补偿，降低噪音对系统稳定的影响。

3 仿真验证

基于Matlab/Simulink环境，搭建如图4所示的直驱式波浪能发电系统模型，验证所提控制方案的跟踪控制效果。

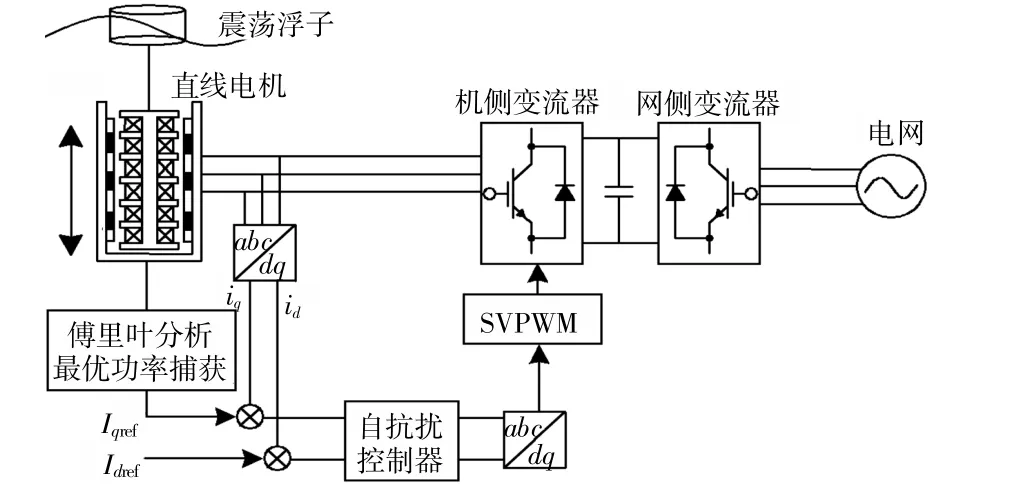
图4 基于自抗扰控制器的直驱式波浪能发电系统模型Fig.4 Model of direct-drive wave power generation system based on ADRC

直驱式波浪能发电系统的相关参数:p=4，M=200 kg，τ=0.05 m，Ψf=0.417 Wb，Rs=2.48Ω，Ld=Lq=0.008 2 H，k=1 000 kg/s2，β=300 kg/s2。

入射波浪不规则激励力的波形如图5所示。

图5 不规则激励力波形Fig.5 The irregular excitation force

图6为随机输入经过加窗傅里变换离散化后的频谱分析图。从图6可以看出，不规则激励下的主频率约为0.5 Hz，其余频段激励可视为干扰信号。将经过傅里叶分析后的主频激励作为系统输入，获取电流目标期望值，对比PI控制方案，验证所提自抗扰控制策略的控制效果。跟踪微分器参数:r=3，h=0.004；扩张观测器与非线性控制率 中 参 数:β1=β2=20，β3=30，kd=15，a1=0.25，a2=0.1，a3=0.15，δ=0.001，b=0.5。

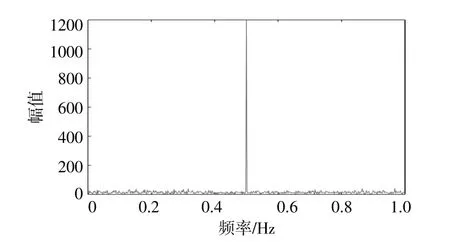
图6 激励力傅里叶变换频谱Fig.6 The Fourier transform spectrum of excitation force

PI控制和自抗扰控制的d轴电流响应如图7所示。

图7 不同控制方案下的d轴电流响应Fig.7 The response of d-axis current under different control schemes

从图7可以看出，基于PI控制器的d轴电流波动明显，误差值较大，而基于自抗扰控制器的系统d轴电流波动较小，跟踪误差绝对值小于1.2 A。

PI控制和自抗扰控制的q轴电流响应如图8所示。从图8可以看出，在相同的主频段波浪激励下，传统PI控制方案与自抗扰控制方案均能实现对目标期望值的跟踪。但相较之下，PI控制方案中的q轴电流跟踪曲线波动及纹波较大，抖振现象明显，且存在一定的相位延迟现象；采用自抗扰控制器的系统，q轴电流可以实现对期望值的平滑跟踪，纹波和抖振小，没有相位延迟现象。

图8 不同控制方案下的q轴电流响应Fig.8 The response of q-axis current under different control schemes

图9反映了不同方案下的q轴电流实际值与期望值之间的跟踪误差。从图9可以看出:PI控制方案下，q轴电流误差值最大可接近10 A，抖振严重；自抗扰方案下的电流误差绝对值小于0.8 A，跟踪误差约为PI方案的1/10，远低于传统PI控制方案，且抖振现象也得到了较好抑制。

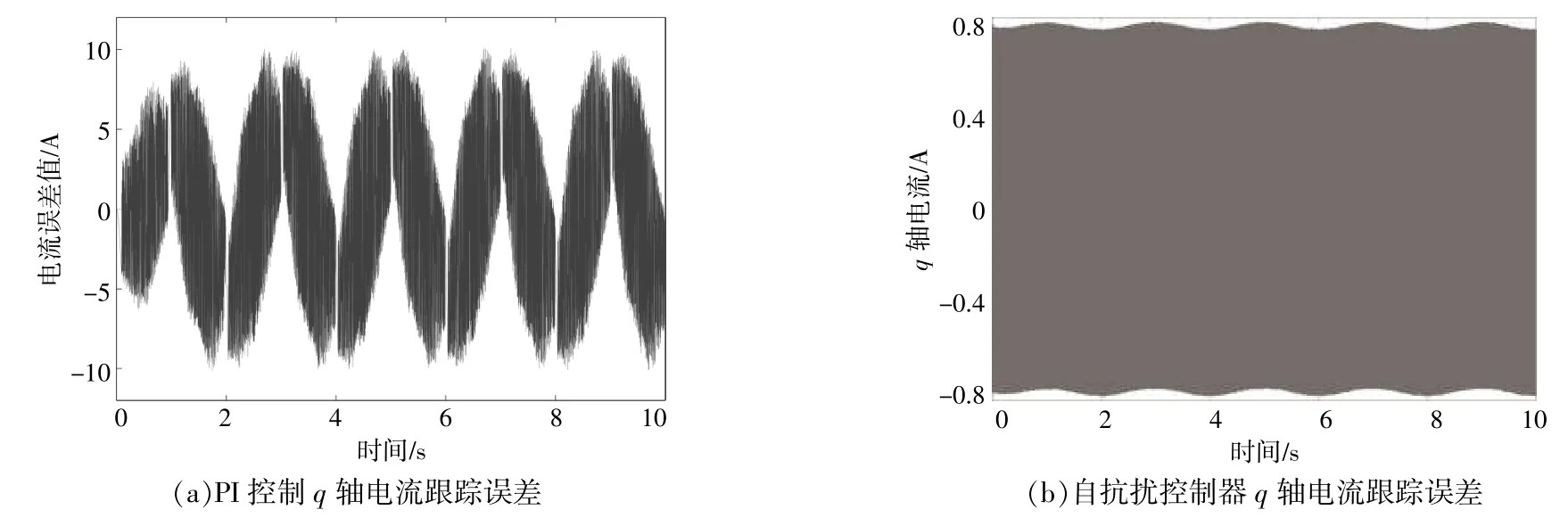
图9 不同控制方案下的q轴电流跟踪误差Fig.9 The q-axis current tracking error under different control schemes

图10反映了不同控制方案下的系统瞬时输出功率。由图10可以看出:在PI控制方案下，q轴电流的抖振与相位延迟现象会导致系统瞬时输出功率波动严重，不利于系统的稳定运行；而自抗扰方案下的系统瞬时功率更平滑，波动更小。

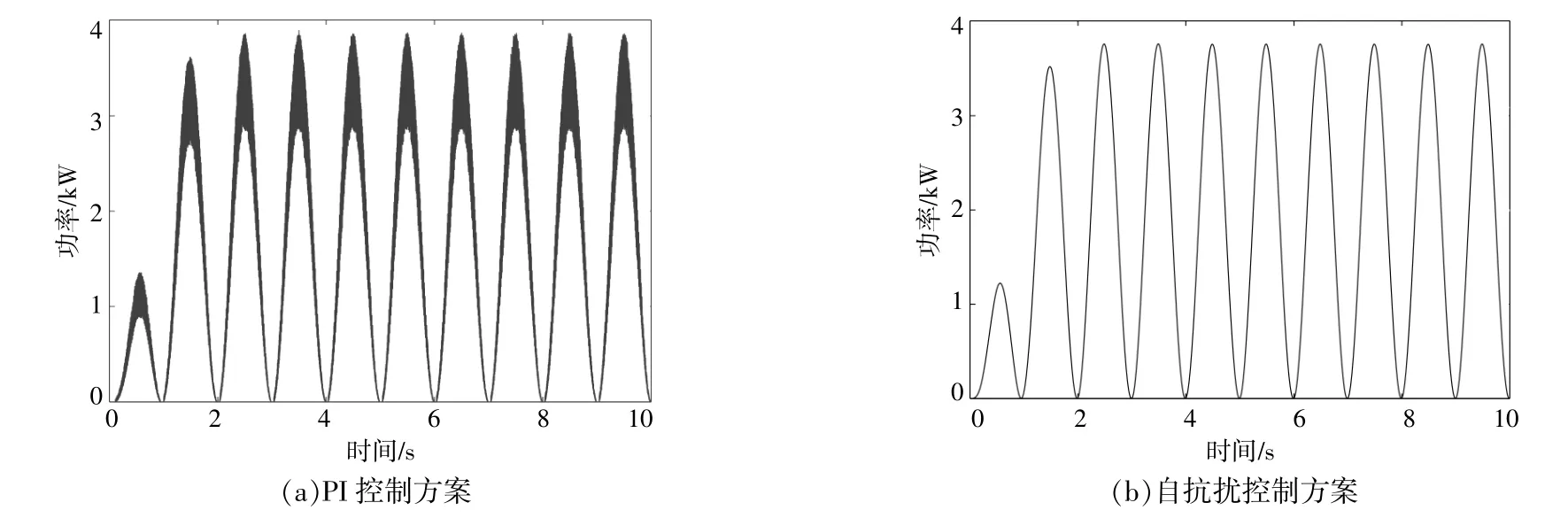
图10 不同控制方案下的系统瞬时输出功率Fig.10 The system instantaneous output power under different control schemes

由图11可知，自抗扰控制方案下的波系统平均输出功率比PI控制方案高出约200 W，波浪能捕获效率更高。

图11 不同控制方案下的系统平均输出功率Fig.11 The system average output power under different control schemes

4 结论

本文分析了直驱波浪能发电系统的水动力学模型及功率方程，针对充满噪音的波浪激励，利用加窗傅里叶变换分析不规则波浪频谱，滤除输入噪音，导出不规则激励下的最大功率捕获条件及电流控制目标，设计自抗扰控制策略，并与传统PI控制方案进行对比。仿真结果表明，所提功率控制策略能有效提取不规则输入主频激励，有效滤除纹波，降低环境噪音影响，降低系统对外界扰动的敏感度；能实时动态跟踪电流期望值，相较于PI控制策略，能有效消除电流跟踪相位延迟，抑制抖振现象，保证系统运行稳定，抗干扰能力与适应性强，使系统瞬时输出功率更平滑，平均输出功率提高。