考虑可再生能源的分布式机组选址定容研究

蒋会哲，张春燕

（1.郑州铁路职业技术学院，河南 郑州 450000；2.黄河科技学院，河南 郑州 450000）

0 引言

以可再生能源为代表的分布式电源（Distributed Generation，DG）在配网中的安装位置和安装容量影响着系统运行成本、系统网损和网络节点电压质量。现阶段针对风机、光伏机组、储能在配网中的选址定容研究内容较丰富。文献[1]提出了基于DG选址定容的配网降损方法。文献[2]提出了基于随机机会约束规划的面向能源互联的主动配电网选址定容方法。文献[3]考虑了风速、光照和负荷之间的相关性，建立了相应的选址定容模型。文献[4]研究了基于智能单粒子算法的DG选址与定容。文献[5]研究了考虑不确定性的三相不平衡配网的DG选址定容。文献[6]提出了计及配电网运行风险的DG选址定容规划方法。文献[7]研究了海上风电场微观选址优化算法。文献[8]研究了抽蓄联合全可再生能源孤岛微网配置优化方法。

上述文献均从可再生能源的优化角度出发，提出了相应的算法和模型，其中:求解方法主要以启发式算法为主，包括NSGA-II算法[9]、多目标粒子群算法[10]、灰狼优化算法[11]以及多智能体遗传算法[12]等；而模型在选址定容方面较为复杂，求解时间较长。这些文献针对DG位置确定的主要原则是接入点网损最小、电压偏移最低、经济性最好等，可以利用优化模型、节点灵敏度等方法确定。这类方法须要考虑的因素较多，并且节点功率受到新能源不确定性的影响有一定波动，在潮流变化较大的情况下选择的位置会随着时间发生变化，因此不利于实际规划。

本文针对节点位置指数模型在DG选址方面的应用进行了建模，利用有功功率变化量确定节点位置指数。建立了可再生能源机组的成本模型和选址定容优化模型，采用改进的磷虾群算法对问题进行求解。最后在IEEE 33节点系统中进行了仿真分析。

1 节点位置指数

节点注入有功和无功功率的变化会导致系统总有功网损的变化。由此，引入节点位置指数（Bus Location Index，BLI），有 功 网 损PL为

式中:N为节点数；ki为与节点i相连的节点；Vi，Vj分 别 为 节 点i，j的 电 压 幅 值；δi，δj分 别 为 节点i和j的电压相角；Gij为节点ij之间的电导矩阵；Bij为节点ij之间的电纳矩阵。

功率平衡等式如下:

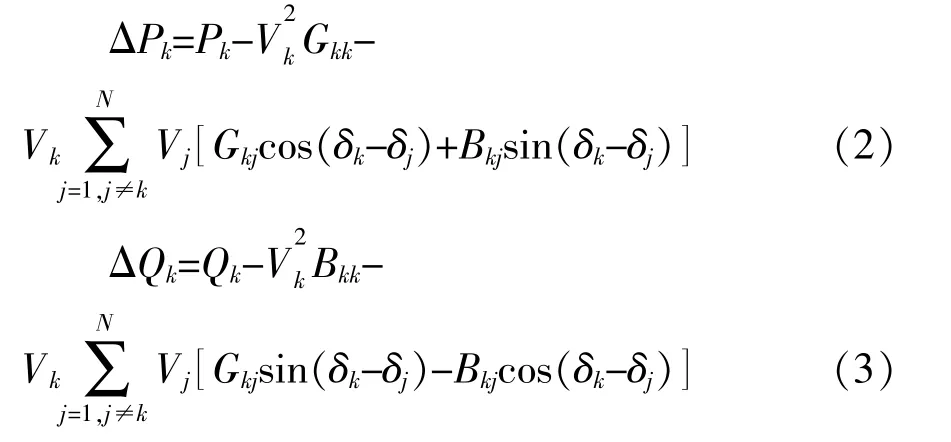
式中:ΔPk，ΔQk分别为支路k的有功功率、无功功率变化量。

有功功率变化量为

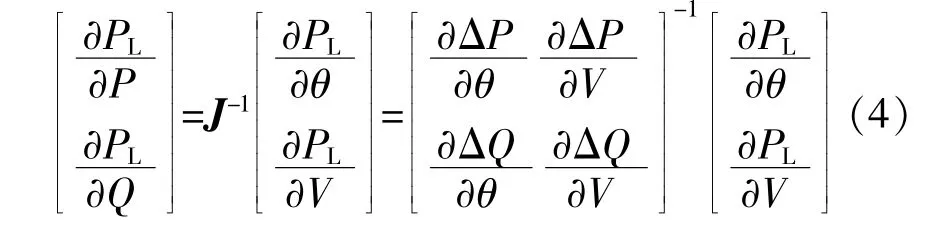
其中，等式左边为网损对有功和无功的变化量，等式右边为雅可比矩阵的逆与网损对相角和节点电压变化量的乘积。

节点位置指数为

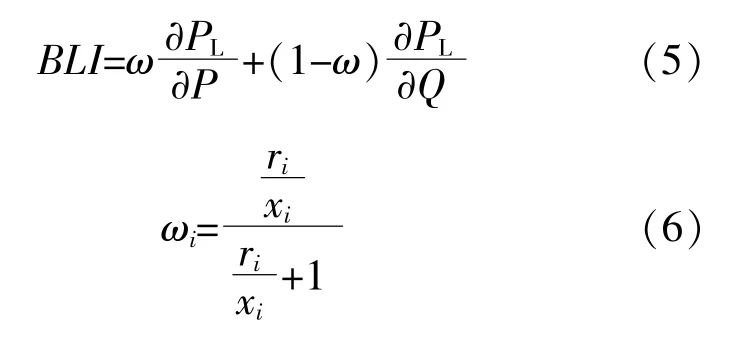
式中:ri为支路电阻；xi为支路电抗；支路权重因子 ωi为所有节点权重因子的均值；考虑到所有节点的参数，ri/xi的变化较小。

通过得到的权重进行降序排列，权重越大的节点则优先安排分布式机组。

2 可再生能源机组的成本模型

通过本文建立的目标函数确定分布式机组的最佳位置和容量，并且考虑可再生能源的运行成本等。

2.1 DG成本

DG机组的成本包括安装成本、燃料成本和运维成本，表达式如下:

式中:CDG为DG成本；PDGi为机组i的有功出力；n为投资年限；r为折现率；C1为资金成本系数；C2为燃料成本系数；C3为运维成本系数；NDG为DG机组数量。

2.2 系统网损

系统有功网损表达式为

系统有功网损成本表达式为

式中:Ik为支路k的电流；Rk为支路k的电阻；C4为网损成本系数；Nb为系统支路总数量。

2.3 污染物排放成本

某些DG机组会产生CO2，SO2和NOx等气体，其排放表达式为

机组的排放成本为

式 中:x1i，x2i和x3i分 别 为 机 组i的CO2，SO2和NOx单位排放量；C5为机组排放成本系数。

2.4 电压偏移成本

可再生能源接入电网后可能引起电压波动，须对电压波动进行优化。

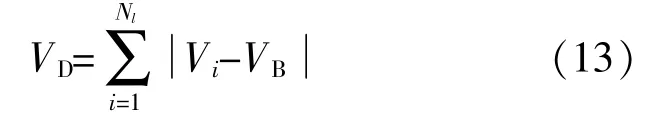
反映到成本上的表达式为

式中:VB为节点参考电压；C6为电压偏移成本系数；Nl为电压测量节点数量。

3 DG选址定容模型

考虑成本因素，对DG的位置和容量进行优化。

（1）目标函数

通过所确定的最优位置，优化系统总成本，得到DG的最佳容量。总的目标函数为

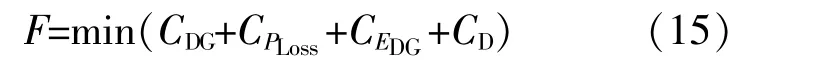
（2）约束条件

①功率平衡约束

系统发出的电量和负荷应当保持动态平衡，具体约束条件为

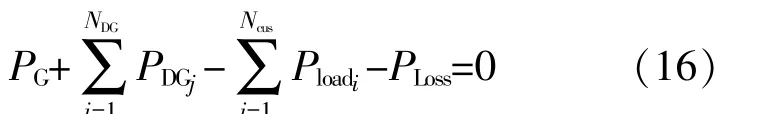
式中:PG为火力机组出力；PDGj为第j个DG机组出力；Ncus为用户负荷节点数量。

②电压约束

网络中电网电压须要保证稳定的范围:

式 中:Vi为 节 点i电 压 幅 值，pu；Vimax，Vimin分 别 为节点i电压的最大值、最小值。

③DG容量限制

考虑到DG渗透率的要求，本文确定渗透率为10%～60%，具体表达式为

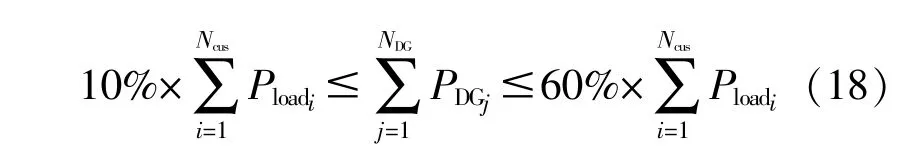
④DG接入后网损约束

即接入DG后的网损应当小于不接入DG的网损。

4 改进磷虾群算法求解DG选址定容模型

磷虾群算法（Krill Herd Algorithm，KHA）是根据磷虾群觅食行为得到的启发式算法[13]。磷虾个体的运动主要分为受其他磷虾个体诱导而移动、自身主动觅食移动和随机扩散3类。该算法能够用于求解连续、离散和非凸问题。算法首先构造初始磷虾种群，计算每个个体的适应度并保留最佳的磷虾个体。优化内容的具体表达式为

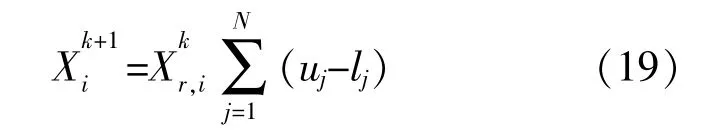
式中:Xi为磷虾i的相对位置；uj，lj分别为边界上界、下界。

磷虾个体的速率表达式为

式中:VNi为因其他磷虾个体移动的影响；VFi为个体觅食行为；VDi为个体的随机扩散行为。

本文提出改进 θ磷虾群算法，即加入相矢量θi，具 体 计 算 表 达 式 为

每个磷虾个体的移动表达式为

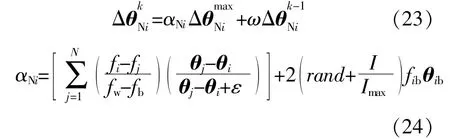
式中:fi为第i个磷虾的目标函数；fj为相邻磷虾的目标值；fw，fb分别为磷虾个体的最坏和最好适应度值；θ为磷虾个体位置；ε为偏差数值，本文取0.002；I为实际迭代次数；Imax为迭代次数最大值；fib为第i个磷虾的最适应度值；θib为第i个磷虾的位置；ω为惯性权重系数，本文取0.8；rand为0～1的 随 机 数。

每个磷虾对周围一定范围的其他磷虾具有正向或反向作用，这个作用的距离称为感应距离，可由下式计算:

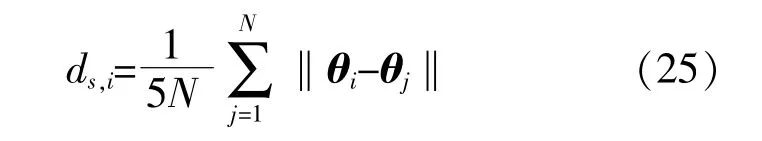
觅食行为与食物的预期位置和磷虾个体对觅食的经验有关。

式中:N为磷虾个体数量；Vf为觅食速度，本文取0.03；ωf为 觅 食 权 重，本 文 取0.85。

随机扩散过程是基于随机方向和最大速度的过程，表达式为

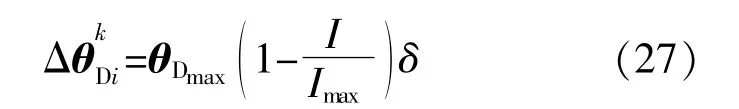
式中:θDmax为个体最大扩散速度；δ为随机方向，介 于[-1，1]。

本文引入交叉和变异过程，得到适应度函数为

针对本文的改进算法，第一阶段为考虑磷虾的莱维飞行，在算法中引入这一随机变量，即:

式 中:L（r）为 莱 维 随 机 过 程。

第二阶段更新每次迭代过程中磷虾的平均数量，具体表达式为

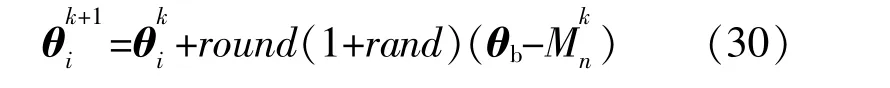
具体的算法流程如图1所示。

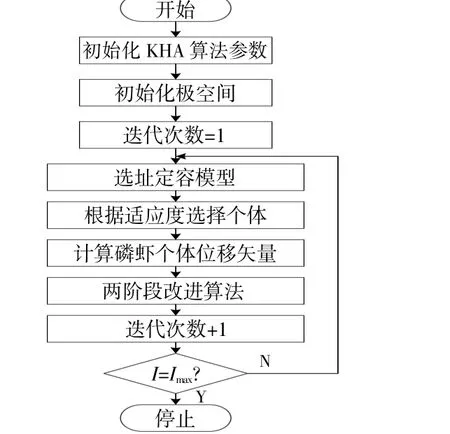
图1 算法流程图Fig.1 Flow chart of the proposed algorithm

结合本文模型，算法的fi为本文所提的目标函数（15），θ对应本文的DG容量，而本文的约束条件则与磷虾个体的最坏和最好适应度值有关。通过迭代求解，最终得到个体最优值和最佳适应度值。

5 算例分析

5.1 系统说明

本文采用IEEE 33节点系统进行仿真，如图2所示。系统根节点为1号节点，系统有功负荷和无功负荷分别为3.56 MW和2.85 MVar，节点电压 为0.95～1.05 pu。

图2 IEEE 33节点图Fig.2 IEEE 33 bus feeder

计算得到各节点的BLI值，具体如表1所示。

表1 BLI相关数据Table 1 Related BLI data pu

BLI指标如图3所示。

图3 BLI指标Fig.3 Graph of BLI

本文考虑5种可再生能源，分别为燃料电池、微汽轮机、风机、光伏和生物质能，其参数如表2所示。每个类型机组均为1台和2台，对比安装前后的情景。

表2 机组数据Table 2 Cost data of units

算法的参数设置为初始磷虾个体为15，最大迭代次数为200。

5.2 算例分析

（1）求解结果分析

利用本文提出的模型和算法，得到1台机组和2台机组下装设的位置和容量，具体如表3和表4所示。

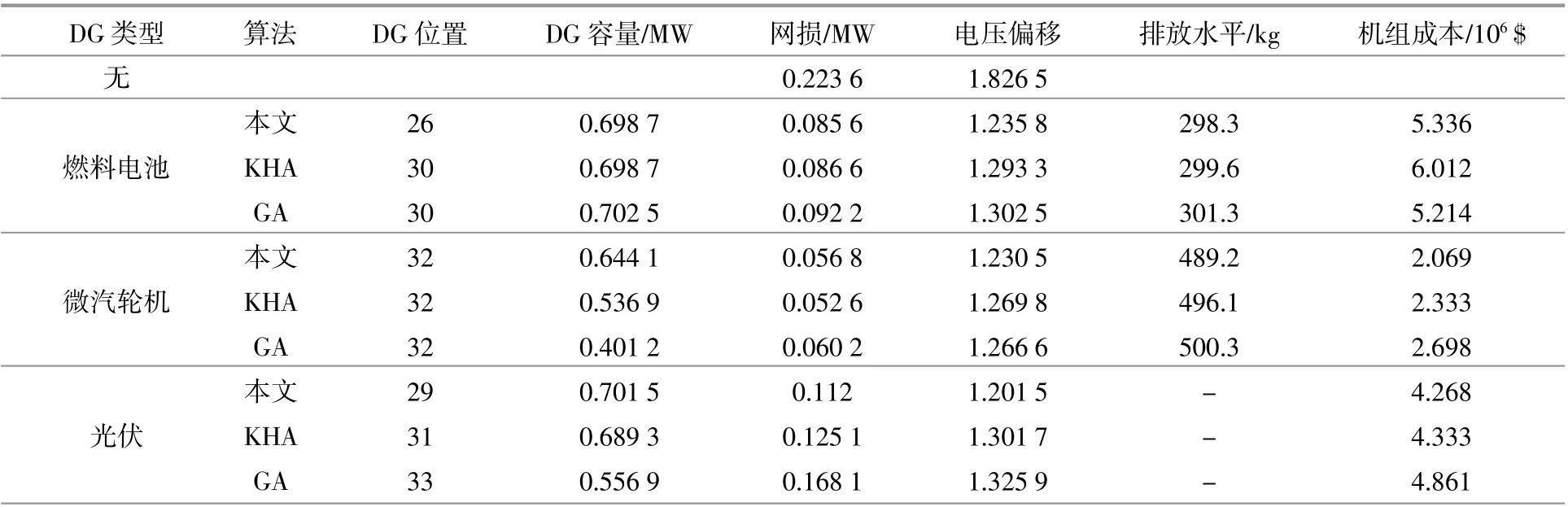
表3 1台机组选址定容结果Table 3 Results of location and sizing of 1 DG

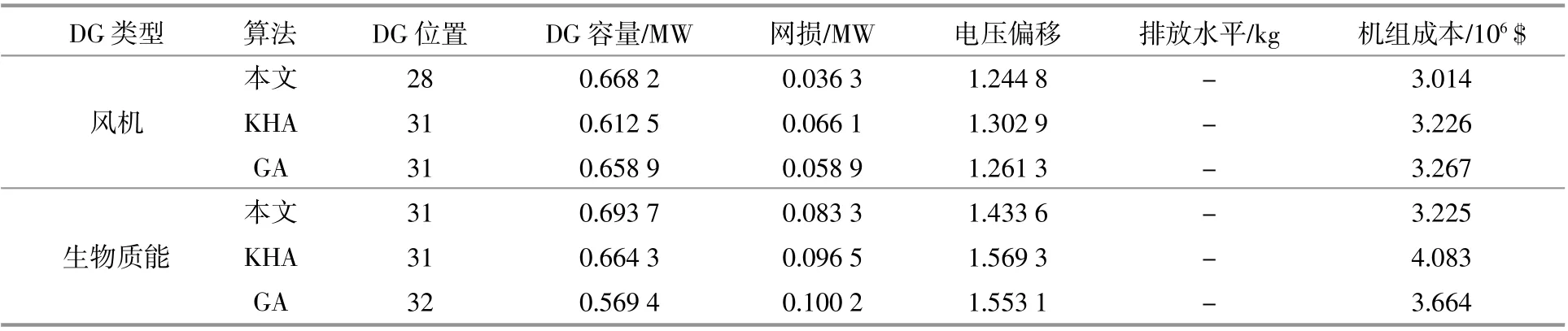
续表3

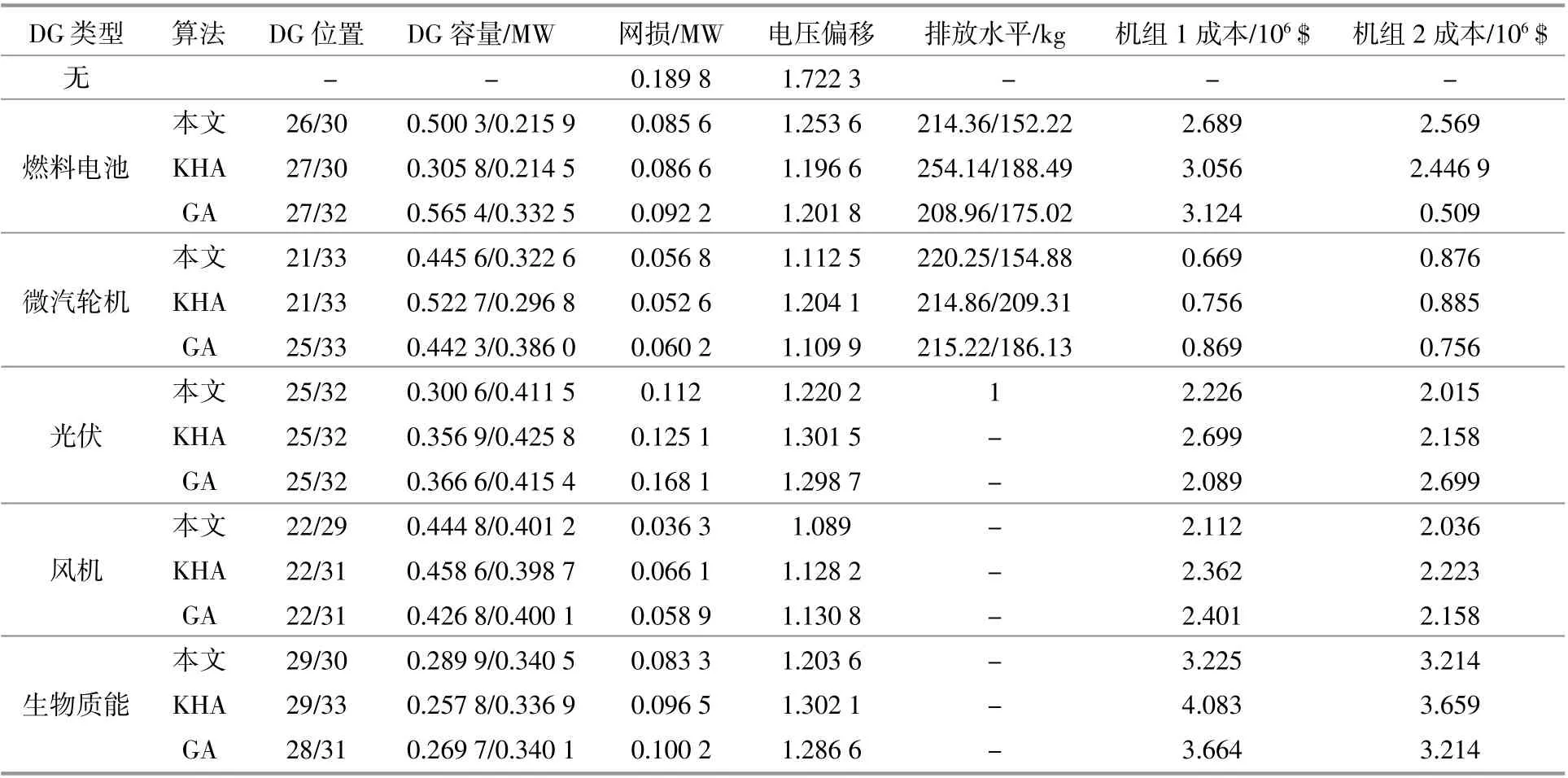
表4 2台机组选址定容结果Table 4 Results of location and sizing of 2 DG

由表3和表4可以看出，分布式可再生能源机组的配置位置与算法的差异不大，而配置容量以及成本则有所差异，本文所提的改进磷虾群算法得到的成本结果最优。纵向对比可以看出，2台机组时的成本、电压偏移及网损值都小于1台机组时的，说明本文所提方法能够适用于大规模可再生能源接入的场景。

利用本文提出的节点指标进行排序，可以大幅缩短计算时间。通过2台机组的电压仿真结果（图4）表明，利用本文方法求解配置节点的电压偏移也得到了最优值。

图4 安装前后电压幅值对比Fig.4 Comparison between size of different phase voltages with and without DGs

（2）改进KHA算法与其他算法对比

针对本文所提算法，利用原始算法与文献[12]的遗传算法（GA）对2台机组的情况进行计算，得到求解耗时如表5所示。

表5 算法求解耗时对比Table 5 Comparison between three algorithms in solving time

风电和光伏机组的对比情况如图5所示。

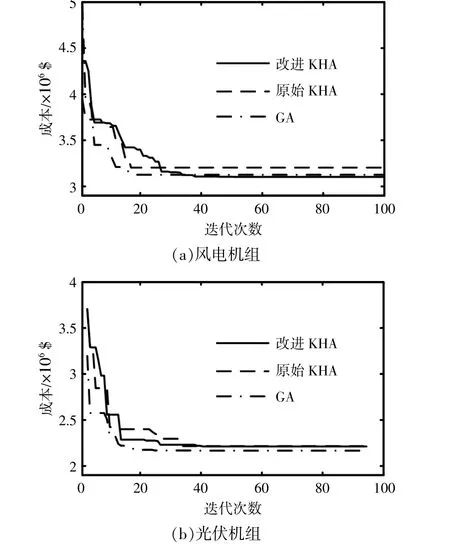
图5 算法的成本收敛情况Fig.5 Convergence comparison in two cases

由图5可以看出，本文所提算法的风电和光伏的收敛性均好于原始算法和遗传算法，这说明本文对原始算法的优化是有效的。

6 结论

本文提出了一种可再生能源机组的选址定容模型。利用节点位置指数确定DG机组的装机位置，能够大大减少运算量，并且该指数与系统的参数相关，能够有效减轻计算量。通过求解结果可以看出，本文所提的算法适用于不同类型机组的选址定容，并且随着机组数量的增加，更能体现算法的优势。通过与其他算法进行对比，说明改进磷虾群算法能够有效提升收敛性，耗时更短。