弱电网对称短路故障期间DFIG风电系统动态稳定性分析

李智玲，张瑞强，姚 骏，于 海，刘瑞阔，刘 远

（1.内蒙古电力（集团）有限责任公司 包头供电局，内蒙古 包头 010400；2.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；3.内蒙古电力（集团）有限责任公司，内蒙古 呼和浩特 010020）

0 引言

双馈感应发电机 （Doubly Fed Induction Generator，DFIG）因其变速恒频、变流器容量小等优 点，成 为 风 电 领 域 的 主 流 机 型 之 一[1]，[2]。然 而，受风能分布的限制，我国风电存在大规模开发、远距离输送的特点，使得设备和电网之间的耦合程度加剧，特别是在弱电网严重短路故障期间，DFIG风电系统极易出现振荡失稳[3]。因此，研究弱电网短路故障期间DFIG风电系统的小信号稳定问题，对增强电力系统安全稳定运行具有重要意义。

目前，国内外对弱电网短路故障期间DFIG风电系统的稳定问题研究较多。文献[4]指出DFIG在严重故障期间，不适当的有功、无功电流注入，会引发风电系统出现失步现象。该现象本质是系统在故障期间是否具有平衡点的问题，是对系统静稳极限的研究。文献[5]将故障期间风力发电系统的稳定问题，划分成了有、无平衡点引起的失步问题和故障持续期间系统的小扰动振荡问题两部分，指出故障程度越严重、线路感抗越大、无功指令越大，风电系统的静态稳定安全域越小，越容易出现失步现象。但文章并未分析弱电网短路故障期间系统的小干扰振荡失稳机理。文献[6]指出随着系统短路比（Short-Circuit Ratio，SCR）不断降低，风电场在故障期间出现小信号失稳的风险越大。文献[7]研究了弱电网故障期 间，锁 相 环（Phase-Locked Loop，PLL）对DFIG风电系统稳定性的影响。但是文献[6]，[7]均忽略了电网和设备之间的耦合作用。

综上所见，弱电网故障期间，DFIG风电系统的小扰动振荡问题并未得到充分的研究。为了分析弱电网故障期间DFIG风电系统的动态行为，本文首先建立了计及线路阻抗的系统详细小信号状态空间模型。基于特征值分析法，对弱电网短路故障期间的DFIG风电系统进行了全面的模态分析，确定了系统最弱阻尼的振荡模态及其主导影响因素，综合评估了不同因素对弱电网故障期间DFIG风电系统小信号稳定性的影响。最后，在Matlab/Simulink中建立了DFIG风电系统的时域仿真模型，通过结果验证了理论分析的正确性。

1 弱电网短路故障期间DFIG风电系统小信号建模

图1给出了电网对称短路故障下DFIG的典型 低电压 穿越（Low Voltage Ride Through，LVRT）控制策略。

图1 LVRT期间双馈风机的控制框图Fig.1 Control block diagram of the DFIG-based wind turbines during LVRT

根据戴维南定理，将电网等效为电压源UG和阻抗ZL的串联。短路故障发生时，为满足电网导则要求，DFIG须要与并网点电压跌落程度成比例的向电网注入无功电流[8]。但在弱电网条件下，由于电网与DFIG控制器之间的耦合程度增加，传统的LVRT策略可能会导致系统小信号失稳。

1.1 DFIG模型

根据电动机惯例，在PLL参考坐标系下，标幺后的DFIG定、转子电流动态方程为

式中:Usdq，Urdq分别为DFIG定、转子电压矢量；Isdq，Irdq分 别 为DFig.、 转 子 电 流 矢 量 ；Ψsdq，Ψrdq分别为DFIG定、转子磁链矢量；Rs，Rr分别为DFIG定、转 子 电 阻；Ls，Lr，Lm分 别 为DFIG定、转 子电感和互感；ωpll为PLL输出的角频率；ωr为转子角频 率；σ为 漏 磁 系 数，σ=1-Lm2/（LrLs）；ωb为 角 速 度 基值。

1.2 PLL模型

在并网型DFIG中，普遍采用PLL获取并网点电压的频率和相位。由图1可得PLL方程为

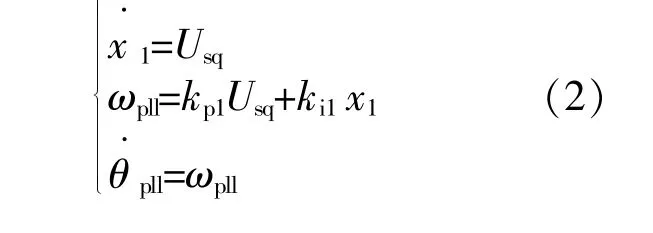
式中:kp1，ki1分别为锁相环PI控制器的比例系数和积分系数。

1.3 转子电流环模型

在LVRT期间，为满足并网导则需求，须控制转 子 侧 变 流 器（Rotor Side Converter，RSC）使DFIG向电网注入无功电流，根据图1可得RSC电流控制环方程为

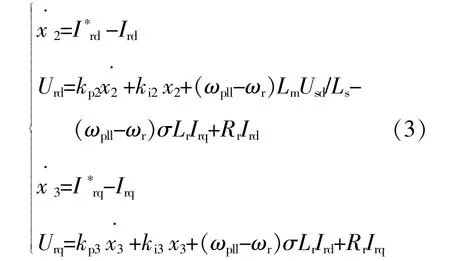
式中:I*rd，I*rq分别为转子电流d，q轴分量指令值；kp2，ki2分别为d轴电流环PI控制器的比例系数和积分系数；kp3，ki3分别为q轴电流环PI控制器的比例系数和积分系数。

1.4 电网模型

LVRT过程中，无功电流注入的任务通常由RSC承 担。网 侧 变 流 器（Grid Side Converter，GSC）负责维持直流母线电压恒定和处理滑差功率。文献[9]表明，GSC的控制对系统稳定性的影响很小。因此，为了简化分析，本文忽略GSC的影响。根据基尔霍夫定律，电网短路故障期间DFIG的总输出电流IGdq为

式中:Cf为网侧滤波电容。

根据图1可知，PLL坐标系下DFIG机端电压与故障点电压之间的关系为

根 据 式（1）～（5），弱 电 网 短 路 故 障 期 间DFIG与电网之间的耦合关系如图2所示。

图2 弱电网对称故障下双馈风机和电网的耦合关系Fig.2 Coupling relationship between DFIG and power grid under weak grid symmetrical fault

由图2可知:由于弱电网条件下传输线路呈现高阻抗状态，短路故障期间DFIG向电网注入的无功电流会对端电压产生严重影响；并且，端电压的动态又会对PLL及RSC电流环产生影响，最后会再次影响到端电压。因此，弱电网故障期间DFIG风电系统的失稳，本质上是在传输线路高阻抗下控制器相互作用引起的振荡失稳。

将式（1）～（5）线性化，弱电网故障期间DFIG风电系统的小信号状态方程可表示为

式 中:Δx，Δu分 别 为 状 态 变 量 和 控 制 变 量；Δx=[ΔIsd，ΔIsq，ΔIrd，ΔIrq，Δx2，Δx3，ΔIGd，ΔIGq，ΔUsd，ΔUsq，Δx1，Δθpll]T；Δu=[ΔUrd，ΔUrq，Δωpll]T。

2 LVRT期间DFIG风电系统的稳定性分析

为了探索弱电网故障期间影响DFIG风电系统不稳定特征根的主导状态变量，本文根据式（6）进行了模态分析。表1给出了不同电网电压跌落程度下，主要状态变量的参与因子和主导特征根的阻尼比。

表1 模态分析结果Table 1 The modal analysis results

由表1可以看出:主导特征根主要受PLL，RSC电流环和端电压的影响，PLL是主导因素；并且随着电网电压跌落程度不断加深，振荡模态的阻尼比由正变负，这表明系统变得不稳定。

2.1 电网电压跌落程度的影响

当弱电网发生对称短路故障时，DFIG须按照电网导则要求向电网注入无功电流。即电网电压跌落程度不仅会影响PLL动态，也关系到故障期间DFIG输出无功电流的大小。图3为不同电网电压跌落程度下DFIG风电系统的特征根轨迹。

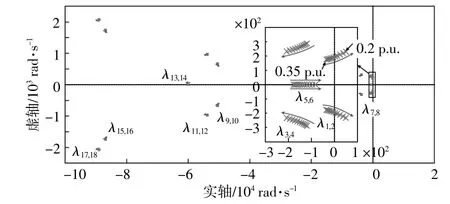
图3 不同电网电压跌落程度的特征根轨迹Fig.3 Eigenvalues locus with different voltage dips degree

由图3可以看出，随着电网电压跌路程度不断加深，主导极点向s平面的右半平面移动。表明弱电网下故障程度越严重，DFIG风电系统就越容易发生小信号失稳，这符合模态分析的结果。

2.2 PLL的影响

根据表1的模态分析可知，PLL是弱电网故障期间影响DFIG风电系统稳定性的主导因素。在弱电网故障期间，若PLL的带宽选择不合适，DFIG风电系统很可能发生振荡失稳。图4为弱电网严重故障下，PLL带宽变化时的根轨迹。本文中弱电网严重故障均指电网电压跌落至0.2 p.u.。由图4可以看出，随着PLL带宽增加，主导不稳定极点移动到了s平面的右半平面。即LVRT期间，适当减小PLL带宽，有利于增强DFIG风电系统的小信号稳定性。但是，随着带宽的减小，PLL的动态响应会被恶化。因此，在弱电网故障期间，选择PLL带宽应注意系统小信号稳定性与PLL动态响应之间的协调。

图4 PLL带宽变化的特征根轨迹Fig.4 Eigenvalues locus with different PLL's bandwidths

2.3 RSC电流环带宽的影响

根据表1的模态分析，RSC电流环的带宽也会影响弱电网故障期间DFIG风电系统的不稳定极点。图5为弱电网严重故障时，RSC电流环带宽变化的特征根轨迹。

图5 RSC电流环带宽变化的特征根轨迹Fig.5 Eigenvalues locus with different current control loop bandwidths of RSC

由图5可以看出，随着弱电网短路故障期间RSC电流环带宽的增加，DFIG风电系统的主导不稳定极点从s平面的右半平面移动到了左半平面。这表明弱电网短路故障期间，增加RSC电流环的带宽可有效改善DFIG风电系统的小信号稳定性。

根据上述的根轨迹分析可知，电网电压跌落程度越深，LVRT期间DFIG风电系统的振荡失稳风险越大。减小锁相环带宽、增加RSC电流环带宽，均可提高弱电网短路故障期间DFIG风电系统的小信号稳定性。但是，RSC电流环带宽受到了变流器开关频率的限制 （MW级风机变流器的开 关 频 率 通 常 为1×103～3×103Hz），无 法 像 根 轨 迹分析中一直增大。因此，在实际应用中，不推荐采用增加RSC电流环带宽的方法，来提高LVRT过程中DFIG风电系统的小信号稳定性。

3 仿真验证

为了验证故障期间DFIG风电系统动态稳定性理论分析的正确性，在Matlab/Simulink中搭建了仿真模型。该风电场由75台2 MW的DFIG风机聚合等效而成[10]，并通过升压变压器和汇集电缆与电网相连。仿真系统的具体参数见表2。仿真模型的短路比为1.8。

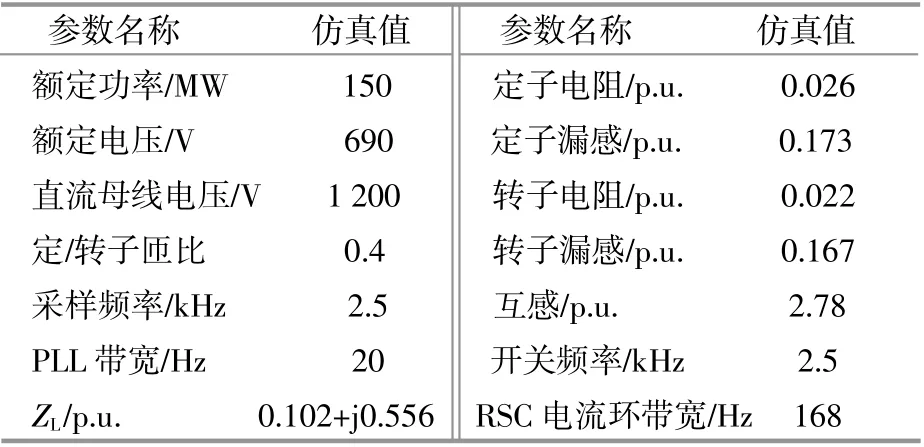
表2 时域仿真系统参数Table 2 Time domain simulation system parameters

3.1 不同电网电压跌落程度的仿真验证

图6为不同电网电压跌落程度下DFIG风电系统的仿真结果。2 s时发生对称短路故障，故障持续1s，其中第1段为故障点电压跌落到0.54 p.u.，第2段为故障点电压跌落到0.24 p.u.。

图6 不同电压跌落程度的仿真结果Fig.6 Simulation results with different voltage dips degree

由图6可以看出，当电压跌落至0.54 p.u.时，DFIG风电系统可以保持小信号稳定，并提供电网导则要求的无功电流。定子A相电压的FFT表明，系统可以稳定运行。当电压跌落至0.24 p.u.时，LVRT过程中DFIG系统发生振荡失稳，此时根据FFT分析结果可知，定子三相电压含有频率为140，240 Hz的振荡分量。说明随着电网电压跌落程度的加深，故障持续期间DFIG风电系统的动态稳定性下降[11]～[13]，这与前文的分析一致。

3.2 PLL带宽变化的仿真验证

图7给出了故障跌落到0.2 p.u.时PLL带宽降低的仿真结果。其中，第1段为PLL带宽降低到17.2 Hz，第2段为PLL带 宽 降低 到12.8 Hz。其参数均与图6中第2段所使用的参数相同。

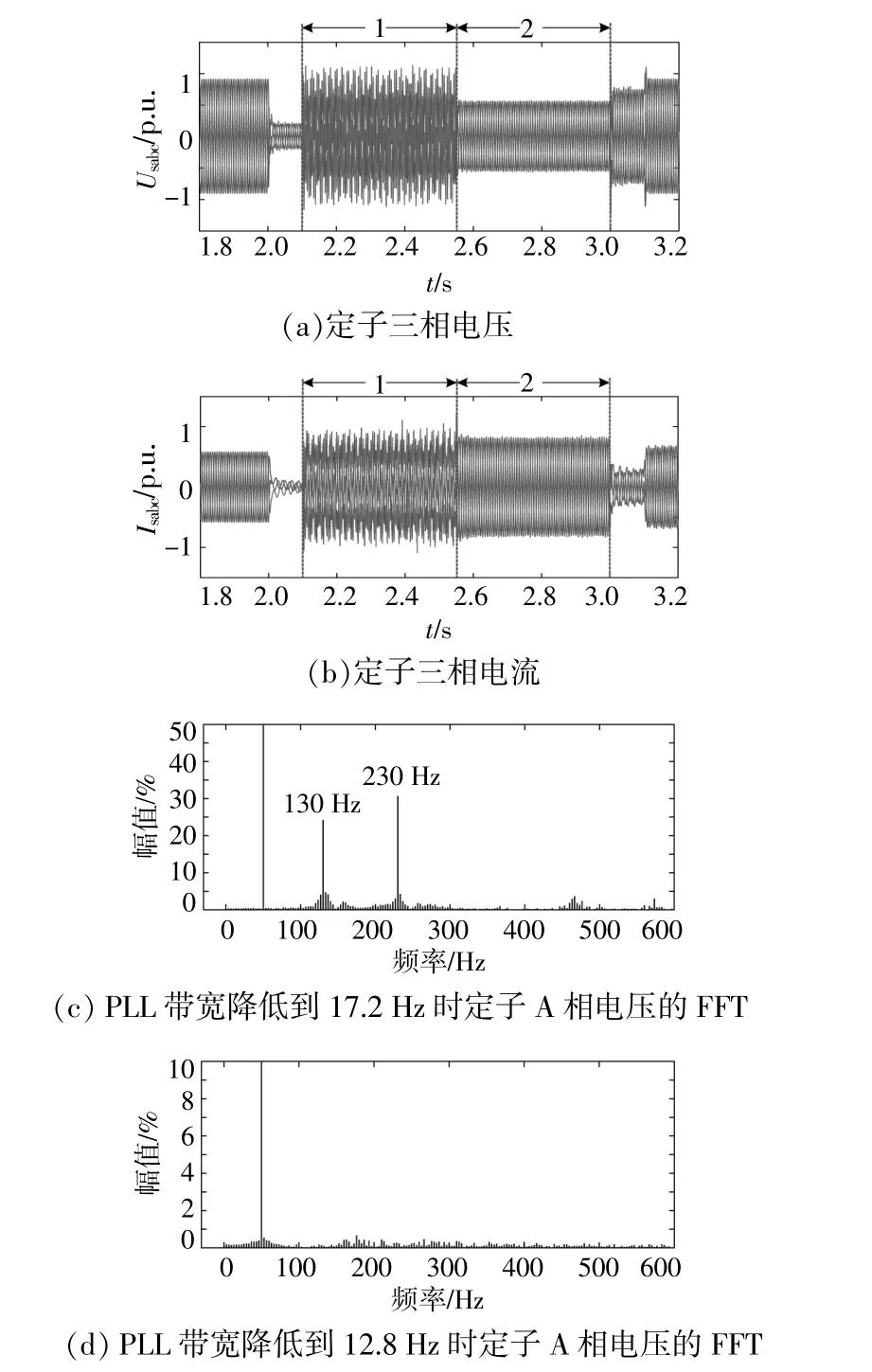
图7 PLL带宽减小的仿真结果Fig.7 Simulation results with decreasing PLL bandwidth

由图7可以看出，当PLL带宽降低到17.2 Hz时，DFIG风电系统依然发生振荡失稳。此时从FFT分析结果可以看出，定子三相电压含有频率为130，230 Hz的振荡分量。对比图6（d），7（c）可知，当故障期间PLL带宽降低后，系统的振荡幅度随之减小。当PLL带宽为12.8 Hz时，故障期间DFIG风电系统的振荡消除，成功实现LVRT。当PLL带宽降低到12.8 Hz时，由定子A相电压的FFT可知，故障期间定子电压质量得到了显著的改善。表明弱电网短路故障期间，DFIG风电系统的动态稳定性随PLL带宽的减小而有所增强[14]，[15]，与前文理论分析相符。

3.3 RSC电流环带宽变化的仿真验证

图8为故障跌落到0.2 p.u.时，RSC电流环带宽变化的仿真结果。其中，第1段的RSC电流环带宽增加到190 Hz，第2段增加到242 Hz。

图8 RSC电流环带宽增加的仿真结果Fig.8 Simulation results with increasing RSC current loop bandwidth

RSC电流环带宽增加到190 Hz时，定子三相电压含有频率为156，256 Hz的振荡分量。对比图6，8可知，随着RSC电流环带宽的增加，系统的振荡幅度减小。当RSC电流环带宽增加到242 Hz时，如 图8（a），（b）第2段 所 示，故 障 期 间DFIG风电系统的振荡得到了有效抑制。当RSC电流环带宽增加到242 Hz时，定子电压的谐波含量随之减小。表明故障时DFIG风电系统的动态稳定性随RSC电流环带宽的增大而增强，与前文分析一致。

4 结论

本文阐述了DFIG风机不同控制环路之间与电网阻抗之间的动态相互作用。指出弱电网故障期间，DFIG风电系统存在振荡失稳的风险，振荡频率呈现宽频特征。根据根轨迹分析，电网电压跌落程度越深，LVRT期间DFIG风电系统的振荡失稳风险越大，而通过减小PLL带宽、增加RSC电流环带宽均可有效提高弱电网短路故障期间DFIG风电系统的小信号稳定性。时域仿真验证了理论分析的正确性。